Физическая химия (1-15 вопросы). Дисциплина Физическая химия
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
|
6. Энтропия как мера неупорядоченности системы. Свободная и связанная энергия. Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций. Энтропия как мера неупорядоченности системы. Энтропия (S) – это мера неупорядоченности движения материи или мера деградации (рассеянности) энергии. Всякая система со временем переходит из неравновесного состояния в равновесное, в процессе такого перехода энтропия всегда увеличивается, а в состоянии равновесия имеет малое значение. Размерность энтропии совпадает с размерностью теплоемкости, однако, теплоемкость и энтропия – не одно и тоже. Теплоемкость характеризует количество теплоты, необходимо для нагревания тела на 1 град, а энтропия характеризует количество рассеянной энергии, приходящийся на 1 град. Энтропия является величиной экстенсивной. 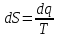 Расчет изменения энтропии при различных термодинамических процессах и при протекании химических реакций. 1) Изохорический процесс V=const 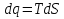 -> -> 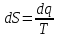 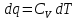 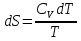 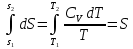 Получаем: 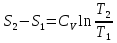 , , 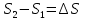  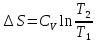 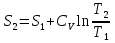 Если ν≠1 моль, то 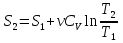 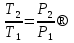 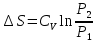 , , 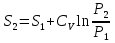 2) Изобарический процесс P=const 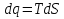 -> -> 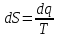 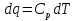 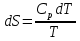 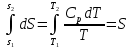 Получаем: 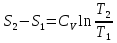 , ,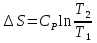 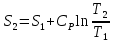 , ,для ν≠1 моль, то 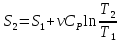 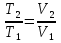 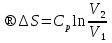 , , 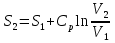 Все вышеприведенные уравнения справедливы для случая, что теплоемкость является величиной постоянной. Однако, известно, что Cp=f(t) и эта зависимость определяется интегральным рядом. Cp=a+bT+cT2+c’T-2 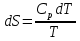 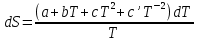 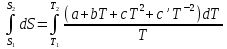 Интеграл суммы – сумма интегралов 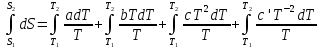 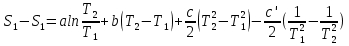 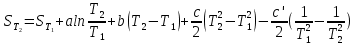 Если требуется определить энтропию при некоторой температуре, а зменение этропии при стандартных условиях известно, то уравнение для химических уравнений будет иметь вид 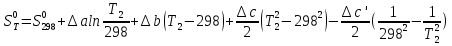 3) Изотермический процесс T=const 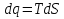 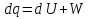 , , 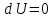 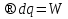 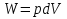 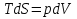 pV=RT 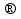 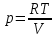 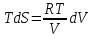 , , 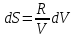 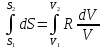 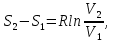 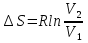 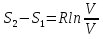 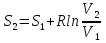 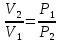 То 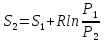 Свободная и связанная энергия. Свободная энергияГиббса (G)есть та работа, которую могло бы совершить тело в обратимом изотермическом процессе, или свободная энергия есть максимальная возможная работа, которую может совершить система, обладая каким-то запасом внутренней энергии. G=U+PV-TS Существует полезное соотношение, связывающее изменение свободной энергии Гиббса ΔGв ходе химической реакции с её константой равновесия K: 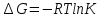 Cвязанная энергия – та часть внутренней энергии, которая не может быть превращена в работу, – это обесцененная часть внутренней энергии. Внутренняя энергия системы U равна сумме свободной (F) и связанной энергии (TS): 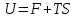 При одной и той же температуре связанная энергия тем больше, чем больше энтропия. При любом необратимом процессе энтропия увеличивается до того, пока не прекратятся какие-либо процессы, т.е. пока не станет F = 0. И это произойдет при достижении замкнутой системой равновесного состояния, т.е. когда все параметры состояния системы (Р, Т) во всех точках системы станут одинаковыми. Вывести систему из этого равновесного состояния, можно только затратив энергию извне.    7. Основные соотношения между термодинамическими функциями. Уравнение Гиббса-Гельмгольца. Соответствующие дифференциалы термодинамических потенциалов: 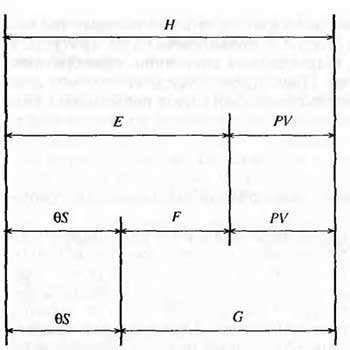
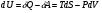 , ,
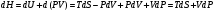
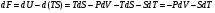 , ,
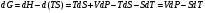 Изохорно-изотермический потенциал. Функции внутренняя энергия U и энтальпия Н редко применяются в химической термодинамике, т.к. условия при которых они характеризуют процесс (V= const, S= const и р = const, S = const) практически неосуществимы. Наибольшее значение имеют характеристические функции: свободная энергия Гельмгольца F = U - T·S - изохорно-изотермический потенциал и свободная энергия Гиббса G = H - T·S - изобарно-изотермический потенциал. Для вывода этих функций воспользуемся обобщенным уравнением I и II законов термодинамики 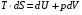 ; ;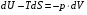 ; ; 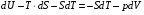 ; ; 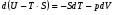 . .Величину U – T ·S обозначим через 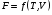 , т. е. F=U – T· S. Тогда , т. е. F=U – T· S. Тогда 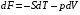 . Так как F=f(Т,V) выражается через U и S, то дифференциал её будет полным, т. е. . Так как F=f(Т,V) выражается через U и S, то дифференциал её будет полным, т. е.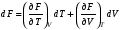 . .Сравнивая это уравнение с уравнением (2.39), получим: 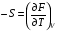 и и 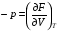 . .Как видно, функция F = U - TS, называемая изохорно-изотермическим потенциалом, также является характеристической. Изобарно-изотермический потенциал обычно обозначается через G (иногда через Z). Она имеет вид: 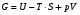 Или Или 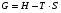 , причем G=f(T, р). , причем G=f(T, р).Уравнение 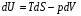 и переписываем его в виде: и переписываем его в виде: 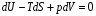 . .К правой и левой частям этого уравнения прибавляем – SdT + Vdp: 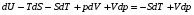 . .В результате 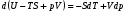 . Выражение в скобках есть G=f(T, р), откуда . Выражение в скобках есть G=f(T, р), откуда 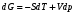 . . Полный дифференциал G=f(T, р) будет 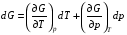 . .Из сравнения этого уравнения с уравнением (2.42) следует, что 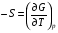 ; ; 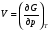 . .Функция 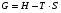 называется изобарно-изотермическим потенциалом. Как и все предыдущие функции, она является функцией состояния, т.е. изменение ее ΔG = G2 - G1не зависит от пути процесса. Из четырех функций U=f·(V,S), H= f·(p,S), F= f·(T,V) и G= f·(T,p) в термодинамических расчетах наиболее часто используются функции Fи G, так как они вычисляются по легко измеряемым параметрам (Т, V, p). называется изобарно-изотермическим потенциалом. Как и все предыдущие функции, она является функцией состояния, т.е. изменение ее ΔG = G2 - G1не зависит от пути процесса. Из четырех функций U=f·(V,S), H= f·(p,S), F= f·(T,V) и G= f·(T,p) в термодинамических расчетах наиболее часто используются функции Fи G, так как они вычисляются по легко измеряемым параметрам (Т, V, p).Уравнение Гиббса – Гельмгольца Рассмотрим изохорно-изотермическую систему (Т = const; V = const) и воспользуемся для характеристики этой системы функцией F = U – T·S. Так как 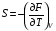 , то, подставив это значение в уравнение функции свободной энергии, получим , то, подставив это значение в уравнение функции свободной энергии, получим 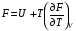 . .Рассмотрим изотермический переход системы из начального состояния в конечное, для которых 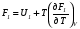 ; ; 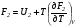 . .Но 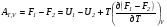 и 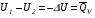 , ,поэтому 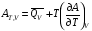 (1) (1)или 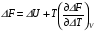 . .Анализируя протекание процесса в изобарно-изотермических условиях (Т = const; р = const), путем аналогичных рассуждений придем к выводу, что 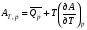 (2) (2)или 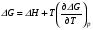 . .Уравнения (1) и (2) выражают величину максимальной работы через тепловой эффект реакции и называются уравнениями Гиббса-Гельмгольца. Из уравнений видно, что теплота может служить мерой химического сродства только при Т = 00 К или при 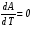 , т. е. при независимости величины работы от температуры. , т. е. при независимости величины работы от температуры.8. Применение второго закона термодинамики к фазовым превращениям. Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения. Интегрирование уравнения Клаузиуса - Клапейрона и его анализ. Применение второго закона термодинамики к фазовым превращениям. Процессы перехода системы из одной фазы в другую называется фазовыми превращениями. К ним относятся процессы плавления, кристаллизации, испарения, кипения, конденсации, сублимации (возгонки) и полиморфные превращения. Температура фазового превращения не зависит от количества равновесных фаз и является величиной постоянной (Т = const). Зависимость температуры фазового перехода от давления была установлена Клапейроном (1834 г.) и обоснована Клаузиусом (1850 г.). Дифференциальная форма уравнения Клапейрона-Клаузиуса имеет вид: 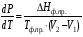 , ,где Н ф.пр. - теплота (энтальпия) фазового превращения, Дж/моль; Т ф.пр. - температура фазового превращения; V1, V2 - объёмы разных фаз. Уравнения Клапейрона-Клаузиуса для частных случаев фазовых превращении: 1) Для процессов испарения и конденсации: 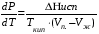 , ,где Нисп.- теплота испарения , Дж/моль; Vп - объём пара, л.; Vж - объём жидкости, л. ; Ткип - температура кипения, град. 2) Для процесса плавления и кристаллизации: 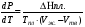 , ,где Нпл.- скрытая теплота плавления, Дж/моль; Vтв- объём твердого тела , л.; Тпл.- температура плавления, град ; 3) Для процесса (сублимации) возгонки: 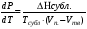 . .где Нсубл. - теплота возгонки, Дж/моль; Тсубл. - температура сублимации, град. 4) Для процесса полиморфного превращения: 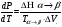 , ,где Н - теплота полиморфного превращения, Дж/моль; Т - температура полиморфного превращения, град. Вывод дифференциальной формы уравнения Клаузиуса - Клапейрона для процесса кипения. Рассмотрим процесс фазового превращения на примере кипения жидкости. Испарение - это фазовый переход на границе раздела жидкость пар или жидкости. Кипение - это процесс, когда парообразование происходит не только с поверхности но внутри жидкости путём образования пузырьков пара жидкости и их выделения. При этом давление в пузырьках пара, находящихся в равновесии с жидкостью, равно давлению пара над жидкостью. Температура кипения - это температура, при которой давление насыщенного пара жидкости равно внешнему давлению: Рнасыщ. пара = Рвнеш. Нормальной называется температура кипения жидкости, измеренная при нормальном давлении. Уравнение Клапейрона-Клаузиуса (5.2.) можно преобразовать, приняв следующие приближения: 1. Поскольку Vп >> Vж (например для воды мольный объем в парообразном состоянии при нормальных условиях равен Vп =22400 см3, а в жидком состоянии Vж = 18 см3), то в уравнении 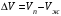 можно пренебречь величиной можно пренебречь величиной 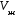 и принять, что и принять, что 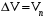 ; ;2. При невысоких давлениях и температурах (вдали от критических) можно применять уравнение состояния идеального газа (уравнение Клапейрона-Менделеева ) и к реальным системам. Тогда 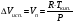 , ,где R - универсальная газовая постоянная. Подставив уравнение 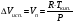 в уравнение К-К в уравнение К-К 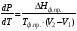 , получим: , получим: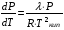 . .Это уравнение после преобразования: 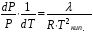 принимает вид: 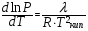 . .Теплота испарения зависит от температуры: c повышением температуры она понижается, а с понижением - повышается; при критической температуре теплота испарения равна нулю. При температурах, далёких от критической, изменения теплоты испарения малы и поэтому в небольшом интервале температур, теплоту испарения можно считать величиной постоянной: =const. Интегрирование уравнения Клаузиуса - Клапейрона и его анализ. Интегрирование уравнения Клапейрона-Клаузиуса 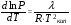 в пределах температур Т1 и Т2, которым соответствуют давления P1 и P2 при =const, дает: в пределах температур Т1 и Т2, которым соответствуют давления P1 и P2 при =const, дает: 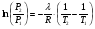 , ,После преобразования последнего получают аналитическую форму уравнения Клапейрона-Клаузиуса: 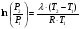 . .Полученное выражение даёт возможность определить: - неизвестное давление по известным температурам, другому давлению и теплоте кипения и известному давлению: 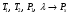 ; ;- неизвестное температуру кипения, по известным давлениям, теплоте кипения и другой температуре: 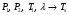 ; ;- теплоту кипения , если известны при двух давлениях насыщенного пара температуры кипения 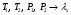 : :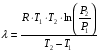 lnрP lnP2 lnP1 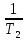 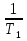 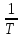 . Неопределённое интегрирование уравнения (5.9) с учётом того, что теплота кипения не зависит от температуры даст уравнение: 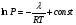 или или 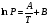 . .Выражения представляют уравнения прямой линии с угловым коэффициентом А в координатах 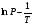 (рис.). (рис.).Рис. Зависимость давления насыщенного пара от температуры. 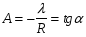 По тангенсу угла наклона прямой можно определить теплоту испарения: граф = Rtg. Чем больше угол , тем больше теплота испарения, и следовательно, тем быстрее испаряется жидкость. Тангенс угла 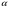 находят из соотношения: находят из соотношения: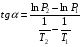 . .Определив теплоту кипения вещества аналитически и графически, можно рассчитать приращение энтропии в процессе кипения: 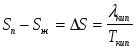 . .9. Химическое равновесие. Классификация равновесных состояний. Признаки равновесных состояний. Закон действующих масс. Вывод константы равновесия для гомогенной реакции. Связь между различными формами выражения констант равновесия. Химическое равновесие. Классификация равновесных состояний. Химическая система находится в равновесии, если её состояние при заданных внешних условиях (например, температуре и давлении) во времени не изменяется. Различают три вида равновесия: - стабильное (устойчивое или истинное); - лабильное (неустойчивое); - метастабильное (относительно устойчивое). Стабильное равновесие характеризуется абсолютным минимумом энергетических характеристических функций. При таком равновесии система, выведенная из равновесия достаточно малым воздействием, самопроизвольно возвращается в исходное состояние после прекращения воздействия на неё. Лабильное равновесие характеризуется тем, что при любом бесконечно малом воздействии система претерпевает такие изменения, в результате которых она переходит в стабильное состояние. Метастабильное равновесие характеризуется относительным минимумом характеристических функций. В этом случае воздействие на систему может привести к конечному изменению в направлении стабильного равновесия, однако, некоторые бесконечно малые изменения вызывают настолько малые изменения в системе, что после прекращения этих воздействий система возвращается в исходное состояние. Равновесие не означает полного покоя в системе. Напротив, при равновесии в системе идут процессы очень энергично, но в противоположных направлениях. С этой точки зрения химическое равновесие является динамичным (подвижным) равновесием. Таким образом, истинное химическое равновесное состояние характеризуется неизменностью состава, подвижностью (динамичностью) и абсолютным минимумом значений характеристических термодинамических функций: G, F. Пределом самопроизвольного протекания реакции при определённых условиях является достижение химического равновесия. Теоретически все химические реакции в большей или меньшей степени обратимы, т. к. в одних и тех же условиях могут протекать в противоположных направлениях. Реакции, сопровождающиеся образованием вещества, выбывающего из участников реакции (образование осадков, газов, малодиссоциируемых веществ, комплексных соединений) называются практически необратимыми, так как скорость обратной реакции столь мала, что не поддаётся измерению. Обратимые реакции никогда не доходят до конца, т. е. до полного исчезновения исходных веществ и превращения их в продукты. Признаки равновесных состояний. Истинное химическое равновесие характеризуется следующими признаками:
Закон действующих масс. Вывод константы равновесия для гомогенной реакции. Многие химические реакции, в зависимости от условий, могут термодинамически протекать самопроизвольно как в прямом так и в обратном направлении. Состав равновесной реакционной смеси характеризуется тем, что концентрации исходных веществ и конечных продуктов находятся по отношению друг к другу в определённом динамическом равновесии. Основным законом кинетики является закон действующих масс, открытый в 1867 г. К.Гульбергом и П.Вааге: Скорость односторонней химической реакции прямопропорциональна произведению концентрации реагирующих веществ, взятых в степенях, соответствующих стехиометрическим коэффициентам. Частная формулировка закона была дана Н. Н. Бекетовым в 1865 г. при изучении давления водорода на скорость вытеснения им металлов из их солей. Химические реакции подразделяются на гомогенные и гетерогенные. Гомогенными называются реакции, протекающие в одной фазе: в смеси газов, в жидком или иногда в твёрдом растворе. Например: CO (г) + Н2O (г) CO2 (г) + H2 (г) , CH3COOH (ж) + C2H5OH (ж) CH3COOC2H5 (ж) + H2O (ж) . Гетерогенными называются реакции, протекающие на границе раздела двух фаз: твёрдое тело – жидкость, твёрдое тело – газ, твёрдое тело – твёрдое тело, жидкость – жидкость. Например: CaO (т) + CO2 (г) CaCO3 (г) , C (т) + O2 (г) CO2 (г) . Рассмотрим обратимую гомогенную реакцию: aA + bB dD + eE, протекающую между веществами в изобарно-изотермических условиях (Р = const и Т = const). Согласно закону действия масс скорости прямой (V1) и обратной (V2) реакции определяются уравнениями: V1 = k1 CaA CbB, V2 = k2 CdD CeE, где k1 и k2 – константы скорости прямой и обратной реакций; CA , CB, CD , CЕ – равновесные концентрации участников реакции; a, b, e, d – стехиометрические коэффициенты; A, B, E, D – участники реакции. В состоянии равновесия скорости прямой и обратной реакций одинаковы: V1 = V2. Имея равенство левых частей уравнения, приравниваем их правые части: k1 CaA CbB = k2 CdD CeE. Разносим в разные стороны константы скорости реакций и равновесные концентрации и получаем: 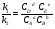 . .Количественной характеристикой химического равновесия служит величина, называемая константой химического равновесия. Константа химического равновесия показывает во сколько раз скорость прямой реакции больше скорости обратной реакции: Кравн = 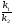 . .Уравнение константы равновесия показывает, что в условиях равновесия концентрации всех участников реакции связаны между собой. Изменение концентрации любого из них вызывает изменение концентраций всех остальных; в результате устанавливаются другие концентрации, но константа равновесия данной химической реакции остаётся величиной неизменной. Таким образом константа равновесия – это постоянная величина, равная отношению произведений равновесных концентраций конечных и исходных участников реакции, взятых в степенях, соответствующих стехиометрическим коэффициентам. Связь между различными формами выражения констант равновесия. Константа химического равновесия может быть выражена различными способами. Если Кравн выражается через равновесные концентрации, то она обозначается Кс и рассчитывается по уравнению: 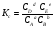 . .Если реакция протекает в газовой фазе, то константу равновесия можно выразить через равновесные парциальные давления участников реакции: 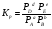 . .Константу равновесия можно выразить через числа молей (n) участников реакции: 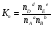 , ,и их мольную долю (N): 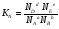 . .Учитывая соотношение между парциальными давлением (Рi, н/м), концентрацией (Сi, моль/м3), числом молей (ni) и мольной долей (Ni) i – компонента. Рi = Ci RT = NiPобщ = 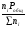 ni = ni = 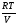 , ,можно вывести формулы связи констант равновесия, выраженных различным способом: Кр = Кс (RT) n, Kp = KN Pобщ n, Кр = Кn 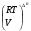 . .n равна разности между стехиометрическими коэффициентами конечных и начальных газообразных веществ в соответствии с уравнениями реакции и определяется по уравнению: n = е + d – a – b. Таким образом, если n 0 и реакция сопровождается изменением числа молей, то имеет место соотношение: Кр = Кс(RT) n = KNPобщn = Kn 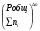 = Kn = Kn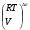 . .Константы равновесия Кn и KN зависят от общего давления. Если n = 0, то все константы равновесия численно равны друг другу при любом способе их вычисления: Кр = Кс = KN = Кn. 10. Химическое равновесие в гетерогенных системах. Расчет константы равновесия. Химическое сродство как мера реакционноспособности системы. Изотерма Вант-Гоффа. Нормальное химическое сродство. Химическое равновесие в гетерогенных системах. Расчет константы равновесия. При выводе закона действующих масс для гомогенных химических реакций предполагается, что все участники реакции находятся в газообразном состоянии. Если система гетерогенная, то есть в реакции участвуют жидкие и твёрдые вещества (так называемые конденсированные фазы), не образующие растворов друг с другом, то при данной температуре парциальные давления указанных компонентов являются величинами малыми и постоянными, так как давление насыщенного пара данных веществ при заданной температуре является постоянным. Эти постоянные величины давлений пара можно внести в константу равновесия, и она, таким образом, будет определяться только равновесными парциальными давлениями газообразных участников реакций. Для реакции FeO + CO Fe + CO2 Константа равновесия запишется так: Кр = 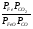 . .Перенесём парциальные давления твёрдых компонентов в левую часть уравнения и обозначая постоянную её через Кр’, получим Кр’= Кр 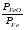 = =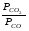 , отсюда: , отсюда:Кр’ = 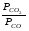 . .Рассмотрим другой пример: термическую диссоциацию (разложения) карбоната кальция: СаСО3(тв) СаО (тв) + СО2(г). Напишем формулу для расчёта константы равновесия данной гетерогенной реакции как для гомогенной: Кр = 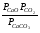 . .Внеся РСаО и РСаСО в константу равновесия, получим Кр 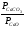 = Кр’, тогда = Кр’, тогдаКр’ = 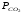 Если 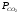 < Kp’, т. е. не достигнуто равновесное давление СО2, то карбонат кальция будет диссоциировать на СаО и СО2. Если < Kp’, т. е. не достигнуто равновесное давление СО2, то карбонат кальция будет диссоциировать на СаО и СО2. Если 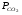 > Kp’, то реакция пойдет в обратном направлении и будет происходить образование карбоната кальция. В обоих случаях через определённое время система приходит в равновесное состояние при условии, когда > Kp’, то реакция пойдет в обратном направлении и будет происходить образование карбоната кальция. В обоих случаях через определённое время система приходит в равновесное состояние при условии, когда 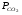 = Кр’. = Кр’.Таким образом, константа равновесия гетерогенной системы определяется парциальным давлением только лишь газообразных компонентов. Давление газообразного продукта рассмотренной реакции называют упругостью диссоциации. Следовательно, упругость диссоциации при определённой температуре в каждом конкретном случае (термической диссоциации карбонатов, бикарбонатов, кристаллогидратов) является совершенно определённой величиной. Химическое сродство как мера реакционноспособности системы. Изотерма Вант-Гоффа. Способность различных веществ взаимодействовать между собой с образованием новых веществ была замечена давно и сначала называлась реакционноспособностью веществ, а позже получила название химического сродства. Химическим сродством называется способность различных веществ вступать в химическое взаимодействие между собой. Долгие годы оставался открытым вопрос, что может служить мерой химического сродства. Решение проблемы было осуществлено с помощью термодинамики, хотя были попытки объяснить химическое сродство сначала скоростью химической реакции, затем величиной теплового эффекта. Вант-Гофф в качестве меры химического сродства предложил использовать максимальную работу, т. е. изменение свободной энергии Гельмгольца, если реакция протекает при постоянном объёме: Wv = -F, или изменение свободной энергии Гиббса, если реакция протекает при постоянном давлении: Wp = - G. Оба термодинамических потенциала удовлетворяют всем требованиям, предъявляемым величине, характеризующей химическое сродство по следующим причинам:
Предположим протекает реакция по схеме: аА + вВ dD + eE. Если все участники реакции находятся в газообразном состоянии и подчиняются законам идеальных газов, то уменьшение изобарного потенциала, которое будет наблюдаться при обратном протекании реакции до состояния равновесия при Р и Т = const, может быть представлено уравнением, которое называется изотермой Вант-Гоффа: Wр = - G = RT(lnKp - ln 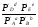 ), (1) ), (1)где Р’А, Р’В, Р’E, Р’D – неравновесные парциальные давления участников реакции; а, в, d, е – стехиометрический коэффициент; Т – абсолютная температура, К; R – универсальная газовая постоянная. Это уравнение показывает, какую работу совершает система при переходе из начального неравновесного состояния в конечное равновесное. Если реакция осуществляется в идеальном растворе при V и Т = const, то изотерма Вант-Гоффа имеет вид: Wv = - F = RT(lnKc - ln 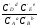 ). (2) ). (2)где С’А, С’В, С’D, C’E - неравновесные концентрации участников реакции. Изменение термодинамических потенциалов (G, F) системы в процессе реакции является количественной мерой химического сродства, которая определяется убылью свободной энергии Гиббса при Р = const (Wp = - G), и убылью свободной энергии Гельмгольца при V = const (Wv = -F). Уравнения (1) и (2) указывают на возможность изменения направления процесса путём варьирования исходного неравновесного состава реакционной смеси, поэтому расчёт величин G и F позволяет оценить термодинамическую возможность протекания реакции в прямом направлении: Если Wр > 0 (G (F) < 0) - реакция протекает самопроизвольно в прямом направлении; Если Wp < 0 (G (F) > 0) - реакция самопроизвольно идти не может (для её прохождения необходим подвод энергии); Если Wр = 0 (G (F) = 0) - система находится в состоянии равновесия. Нормальное химическое сродство. Для того, чтобы можно было сравнивать сродство различных веществ, было введено понятие нормального химического сродства. К уравнению нормального химического сродства легко перейти из уравнения изотермы Вант-Гоффа, если предположить, что исходные концентрации или исходные парциальные давления всех участников реакции равными единице, тогда уравнения изотермы Вант-Гоффа упростятся и убыль нормальной свободной энергии примет вид: G0 = Wр = RTlnKp, F0 = Wv = RTlnKc. где G0 и F0 – нормальное химическое сродство или мера химического сродства.Сравнивая Wv и Wp различных веществ, можно получить характеристику степени их удалённости от состояния равновесия при концентрации каждого из них Сi = 1 моль/л или парциальном давлении Рi = 1атм. 11. Зависимость константы равновесия от температуры. Уравнение изобары Вант-Гоффа в дифференциальной и интегральной формах. Уравнение изохоры Вант-Гоффа в дифференциальной и интегральной формах. Зависимость константы химического равновесия от температуры выводится, во-первых, из уравнения нормального химического сродства: - G0 = Wр = RTlnKp, и, во- вторых, из уравнения Гиббса-Гельмгольца: G0Т = H0Т –TS0, G0Т = H0Т – T 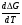 , ,удобно сочетающих первый и второй законы термодинамики применительно к обратимым изотермическим процессам, где Н0Т – тепловой эффект реакции, Дж/моль, S0 – изменение энтропии, Дж/мольК. Для нахождения зависимости константы химического равновесия от температуры возьмём производную по температуре из уравнения изотермы и подставив значение G и её производной по температуре в уравнение (4.22), получим уравнение: - RTlnKp = H0Т – RTlnKp – RT2 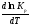 . .Сократив одинаковые члены уравнения и сделав соответствующие преобразования, получим: 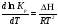 , (1) , (1)где 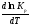 – температурный коэффициентконстанты химического равновесия. – температурный коэффициентконстанты химического равновесия. Выражение (1) называется уравнением изобары Вант-Гоффа в дифференциальной форме. Если процесс протекает при постоянном объёме, то зависимость константы равновесия от температуры определяется уравнением изохоры Вант-Гоффа, которое выводится аналогичным образом: 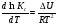 , ,где U – стандартное изменение внутренней энергии системы. Для реакций, протекающих в неидеальных растворах, в уравнении изохоры Кс заменяется на Ка (концентрация (с) заменяется на активность (а)), при этом получается: 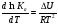 . .Анализ уравнений изобары и изохоры показывает, если реакция протекает с выделением теплоты (H < 0, U < 0), то температурный коэффициент константы равновесия меньше нуля: 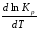 < 0; < 0; 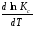 < 0; < 0; 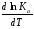 < 0. < 0.Следовательно, с повышением температуры константа равновесия экзотермических реакций уменьшается и равновесие смещается в сторону обратной реакции. Если Н > 0 и U > 0 реакция протекает с поглощением тепла, т. е. является эндотермической, то: 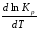 > 0; > 0; 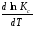 > 0; > 0; 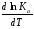 > 0. > 0.Это означает, что с ростом температуры константа равновесия эндотермической реакции всегда увеличивается и равновесие смещается в сторону прямой реакции (вправо). Отсюда вывод: экзотермические реакции необходимо проводить при пониженной, а эндотермические – при повышенной температуре, так как наибольшая полнота эндотермических реакций достигается при возможно более высоких температурах, а наибольшая полнота экзотермических реакций – при более низких температурах. И наконец, если Н = 0, то константа равновесия Кр не зависит от температуры. Эти же выводы получаются из принципа смещения равновесия Ле-Шателье-Брауна (1885-1886 гг.): Если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-либо из условий, определяющих состояние равновесия, то в системе усилится то из направлений процесса, течение которого ослабляет влияние произведённого воздействия, и положение равновесия сместится в том же направлении. Так в реакции 3Н2 + N2 2NH3 H0298 = - 46,2 кДж/моль при понижении температуры и повышении давления усиливается экзотермическая реакция синтеза аммиака, сопровождающаяся уменьшением объёма, так как только таким путём может быть ослаблен эффект внешнего воздействия. Для использования уравнений Вант-Гоффа для практических расчётов следует проинтегрировать дифференциальные уравнения изобары и изохоры в пределах двух температур с учётом того, что тепловой эффект реакции в небольшом температурном интервале изменяется незначительно и его можно считать условно постоянным. При таком допуске интегрирование уравнения (1) 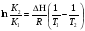 . (2) . (2)Уравнение (2) называется интегральной формой изобары Вант-Гоффа, оно позволяет: Во-первых, вычислить стандартный тепловой эффект реакции Н0 по экспериментально найденным при двух температурах константам равновесия; Во-вторых, вычислить константу равновесия при заданной температуре, если известный стандартный тепловой эффект реакции и константа равновесия при стандартной температуре. Интегральная форма изобары Вант-Гоффа аналогично: 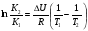 Более точное значение теплового эффекта реакции, учитывающее его зависимость теплоёмкости от температуры Т, рассчитывается по закону Кирхгофа: Н0Т = Н0298 + 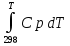 , ,где H0298 - стандартная энтальпия, Дж/моль; Ср – изменение теплоёмкости веществ в процессе реакции. Неопределённое интегрирование уравнения изобары Вант-Гоффа (4.27) даёт линейное уравнение: 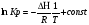 . (3) . (3)При переходе к десятичному логарифму получим: 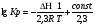 . (4) . (4)Обозначим постоянные слагаемые буквами А и В, тогда уравнение примет вид: lnKp = 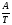 + B. (5) + B. (5)Выражения (3)-(5) удобны для графического анализа процессов, так как зависимость в координатах lnKp = f (1/T) представляет собой прямую линию, где А = - 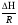 - угловой коэффициент прямой, а В = const - отрезок ординаты, отсекаемой этой прямой и равный lnKp при 1/Т = 0. - угловой коэффициент прямой, а В = const - отрезок ординаты, отсекаемой этой прямой и равный lnKp при 1/Т = 0.α lnK 1/T α lnK 1/T Рис. Зависимость логарифма константы равновесия от величины обратной температуры. Из уравнения (5) и рисунка видно, что логарифм константы равновесия линейно зависит от обратного значения температуры, при этом, если Н < 0, реакция является экзотермической, прямая на графике lnK = f(1/T) образует тупой угол и константа равновесия с ростом температуры увеличивается. И, наоборот, если Н > 0, реакция является эндотермической, угол оказывается острым, константа равновесия увеличивается с понижением температуры. 12. Расчет равновесных состояний с помощью таблиц стандартных термодинамических величин и по методу Тёмкина-Шварцмана Расчет химического равновесия с помощью таблиц стандартных термодинамических величин В настоящее время при расчетах химических равновесий широко используют таблицы термодинамических величин, где приведены вычисленные с большой точностью термодинамические характеристики веществ в стандартном состоянии. Газы и растворы в стандартном состоянии считаются идеальными. Расчет ΔG и Кр целесообразно разделить на два этапа: 1) Сначала вычисляют изменение изобарного потенциала реакции для условий, принятых за стандартные (температура 298, 150К; давление, под которым находится каждое из чистых веществ – 1 атм). Стандартные изменения энтальпии, изобарного потенциала и стандартную энтропию принято обозначать ΔН2980,ΔG2980 и ΔS2980. По величине и знаку ΔG2980определяют возможность реакции. Если ΔG2980 >0 и абсолютное значение ΔG2980 очень велико, то реакция в стандартных условиях неосуществима и, следовательно, все другие расчеты не имеют смысла. Обычно в таблицах представлены теплоты образования ΔН0 соединений из простых веществ. Очевидно, что ΔН0 простых веществ, находящихся в стандартном состоянии, равны нулю. В таблицах приводится также - ΔG0 – убыль энергии Гиббса при образовании одного киломоля вещества из элементов, находящихся в стандартном состоянии. Для элементов в стандартном состоянии ΔG0 =0. В термодинамических таблицах приводятся еще абсолютные значения энтропии ΔS0 веществ в стандартном состоянии. Для иллюстрации рассчитаем в общем виде ΔН2980,ΔG2980 и ΔS2980 реакции. NH3 + HCl ↔NH4Cl; 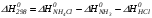 , ,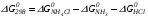 , ,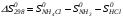 . .2) Затем от найденного значения ΔG2980 переходят к значению ΔGТ0 при температуре, отличной от температуры 2980 К; далее определяют константу равновесия, состав равновесной смеси и выход продуктов реакции. В соответствии с уравнением (2.41) ΔGТ0 = ΔНТ0 - ТΔS0 для перехода от ΔG2980 к ΔGТ0 необходимо пересчитать ΔН2980на ΔНТ0и ΔS2980 на ΔSТ0для заданной температуры. Чтобы определить значения термодинамических характеристик при других температурах и давлениях, надо использовать выведенные ранее соотношения. Метод Темкина–Шварцмана Для практических целей приходится константу равновесия вычислять при температурах более высоких, чем стандартные. Для этого необходимо знать ΔGТ0, ΔНТ0 и ΔST0. Значительные сокращения математических операций при подсчете указанных величин достигаются методом, предложенным М. И. Темкиным и Л. А. Шварцманом. Возьмем определенный интервал из уравнения Кирхгофа (1.33) в пределах от 298 до Т К, при этом получим 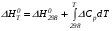 . (1) . (1)Для расчета изменения энтропии химической реакции проинтегрируем в тех же пределах уравнение 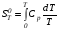 , где вместо теплоемкости одного вещества следует подставить изменение теплоемкости ΔСрсистемы: , где вместо теплоемкости одного вещества следует подставить изменение теплоемкости ΔСрсистемы: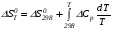 . (2) . (2)Значения (1) и (2) подставляем в уравнение 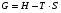 : :ΔGT0 = ΔНТ0 -Т ΔST0. При этом получим 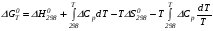 . .Подставим в подынтегральные выражения эмпирический степенной ряд: ΔСр = Δа + Δв Т + ΔсТ2, 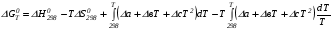 . .Интегрируя, получим 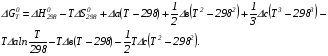 Раскроем скобки: 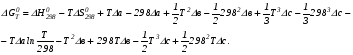 Сгруппируем члены относительно температурных коэффициентов Δа; Δв и Δс:  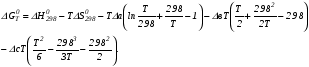 Обозначим: 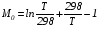 ; ; 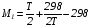 ; ; ; ;  . .Подставив Мi в уравнение (4.22), получим  . .Выражение для Мn справедливо, начиная с М1. Коэффициенты М0… Мnзависят только от температуры. Они рассчитаны и представлены в справочной литературе. 13. Термодинамика и законы разбавленных растворов. Понижение давления пара растворителя над раствором. Закон Рауля. Среди растворов особенно интересны такие, для которых во всей области концентраций соблюдается простейшая линейная зависимость парциальных и общего давлений пара от концентрации. Если концентрацию выражать в мольных долях, то  ; ; 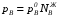 ; (1) ; (1)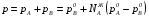 ; ;где 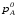 и и 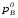 - давления насыщенного пара чистых компонентов А и В при данной температуре; - давления насыщенного пара чистых компонентов А и В при данной температуре; 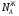 и и 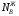 - мольные доли компонентов в жидкой фазе. - мольные доли компонентов в жидкой фазе.Уравнения (1) являются математическим выражением закона Рауля, согласно которому при постоянной температуре парциальное давление napа каждого компонента равно давлению пара этого компонента в чистом виде, помноженному на его мольную долю в растворе. Для бинарного раствора, состоящего из компонентов А и В (А - растворитель) удобнее использовать другую формулировку: Относительное понижение парциального давления пара растворителя над раствором не зависит от природы растворённого вещества и равно его мольной доле в растворе. 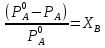 РА0 РВ0 РВ=РВ0NВЖ Р=РА+РВ Р=РА0РАЖ |
