Физическая химия (1-15 вопросы). Дисциплина Физическая химия
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
|
4. Зависимость теплового эффекта от температуры. Уравнение Кирхгоффа в дифференциальной и интегральной форме. Зависимость теплового эффекта от температуры. Рассмотрим зависимость теплоты процесса от температуры. Для этого возьмем частные производные от приращения функций из уравнений теплоемкости 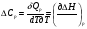 и и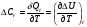 : :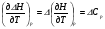 ; ; 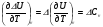 , ,где 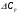 , , 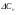 - изменение теплоемкости в результате протекания процесса при р = const или - изменение теплоемкости в результате протекания процесса при р = const или 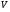 = const. = const.Отсюда получаем: 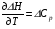 ; ; 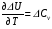 . .Уравнения 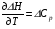 и и 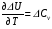 называют уравнениями Кирхгофа. Левая часть уравнений представляет собой температурный коэффициент процесса. Тогда следует, что температурный коэффициент процесса (реакции, фазового перехода и т.д.) равен приращению теплоемкости в результате протекания этого процесса. называют уравнениями Кирхгофа. Левая часть уравнений представляет собой температурный коэффициент процесса. Тогда следует, что температурный коэффициент процесса (реакции, фазового перехода и т.д.) равен приращению теплоемкости в результате протекания этого процесса.Для химической реакции аА + вВ 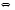 dD + еЕ dD + еЕприращение теплоемкости определяется выражением: 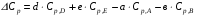 или 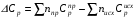 , ,где 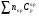 и и 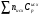 - сумма теплоемкостей соответственно продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов. - сумма теплоемкостей соответственно продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов.Из уравнений Кирхгофа следует, что если приращение теплоемкости положительное, то температурный коэффициент процесса и тепловой эффект с ростом температуры становятся положительными, и наоборот, при ΔСр > 0 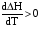 ; ;при ΔСр< 0 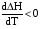 ; ;при ΔСр = 0 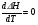 и ΔН = const. и ΔН = const.Из вышеизложенного следует: изменение теплоемкости системы (при переходе её из начального в конечное состояние) является температурным коэффициентом теплового эффекта, который показывает, насколько изменится тепловой эффект (в изохорном или изобарном процессах) при изменении температуры на один градус. По закону Кирхгофа определяется, как уменьшается энтальпия (или тепловой эффект Q = - ΔН ) в изобарном процессе, если изменяется температура протекания процесса. Для этого нужно в выражении 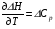 разделить переменные и проинтегрировать: разделить переменные и проинтегрировать: 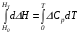 . .Получаем уравнения Кирхгофа в интегральной форме: 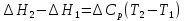 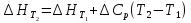 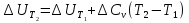 Уравнение 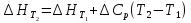 даёт возможность вычислить тепловые эффекты реакции при любой температуре, если известны теплоёмкости всех участников реакции в рассматриваемом интервале температур и тепловой эффект реакции для какой-либо одной температуры, например, для стандартной. Тогда уравнение Кирхгофа в интегральной форме примет вид: даёт возможность вычислить тепловые эффекты реакции при любой температуре, если известны теплоёмкости всех участников реакции в рассматриваемом интервале температур и тепловой эффект реакции для какой-либо одной температуры, например, для стандартной. Тогда уравнение Кирхгофа в интегральной форме примет вид:Н0 Т = Н0 298 + Ср (Т – 298). Известно, что для многих веществ теплоёмкость не является величиной постоянной. Для химической реакции изменение теплоёмкости определяется следующим образом: Cp = а + в Т + с Т2 + с’/ T2 . После подстановки этого уравнения в уравнение Кирхгофа, и интегрирования в неопределённых пределах получаем: HТ = H0 + аТ + в/2 Т2 + с/3 Т3 + с’/ T. (1) H0 - постоянная интегрирования, которая определяется по полученному опытным путём тепловому эффекту при одной температуре. Интегрирование уравнения после подстановки (2.40 в 2.36) можно провести в интервале температур от Т1 до Т2. При этом получим следующее уравнение: HТ2 = HТ 1 + а·(Т2 – Т1) + (в/2)·(Т22 – Т21) + (с/3)·(Т32 – Т31) + с’·(1/T1 – 1/Т2). (2) Если Т1 = 298 К, а Т2 = Т то получаем урвавнение: HТ = H0298 + а·(Т – 298) + (в/2)·(Т2 – 2982) + (с/3)·(Т3 – 2983) + с’·(1/298 – 1/Т). (3) Для органических веществ это уравнение будет иметь вид HТ2 = HТ1 + а·(Т2 – Т1) + (в/2)·(Т22 – Т21) + (с/3)·(Т32 – Т31) + d/4·(Т42 – Т41). (4) Следует отметить, что интегральные уравнения Кирхгофа в развернутом виде справедливы только в том интервале температур, для которого справедливы эмпирические уравнения теплоёмкостей веществ, участвующих в реакции: Ср = а + вТ + сТ2; Ср = а + вТ + с’ Т-2; Ср = а + вТ + сТ2 + dТ3 . Уравнения (1)-(4) называются интегральными уравнениями Кирхгофа в развернутом виде. Зависимость теплового эффекта от температуры. Для простейшей термодинамической системы – идеального газа – теплоёмкость не зависит от температуры и мольного объёма, т. е. Ср = const. Отсюда: Нид.газ = Ср (Т2 –Т1). (2.32) Расчёт тепловых эффектов химических реакций по теплотам образования даёт точные результаты только для стандартной температуры. Чтобы рассчитать тепловой эффект химической реакции при температурах, отличных от стандартной, необходимо знать температурный коэффициент. Температурным коэффициентом теплового эффекта называется приращение теплового эффекта, при повышении температуры на 1 градус. Зависимость теплового эффекта реакции от температуры при постоянном давлении определяется уравнениями: Ср = 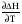 ; Ср = ; Ср =  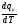 . (2.33) . (2.33) а при постоянном объёме - Сv = 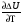 ; Сv = ; Сv = 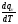 . (2.34) . (2.34)Уравнения (2.33) и (2.34) называются дифференциальной формой уравнения Кирхгофа. Температурный коэффициент теплового эффекта равен изменению суммарной теплоёмкости системы при протекании реакции. Так для реакции: а А + вВ сС + дД изменение теплоёмкости в ходе её определится по уравнению: С = с С (С) + d С (Д) - а С (А) – в С (В), где а, в, с, d – стехиометрические коэффициенты; A, B, C, Д – участники реакции. Или в общем случае: С = nпродCпрод - nисхCисх. С – разность сумм молярных теплоемкости (Ср или Cv) продуктов реакции и исходных веществ, взятых с учётом стехиометрических коэффициентов. Разносим переменные в дифференциальном уравнении, интегрируем его и получаем уравнение Кирхгофа в интегральной форме: dH = Cp dT, (2.35) HT2 T2 dH = Cp dT , (2.36) HT 1 T1 или HT2 = HT 1 + Cp (T2 – T1). (2.37) Уравнение (2.37) даёт возможность вычислить тепловые эффекты реакции при любой температуре, если известны теплоёмкости всех участников реакции в рассматриваемом интервале температур и тепловой эффект реакции для какой-либо одной температуры, например, для стандартной. Тогда уравнение Кирхгофа в интегральной форме примет вид: Н0 Т = Н0 298 + Ср (Т – 298). (2.38) Известно, что для многих веществ теплоёмкость не является величиной постоянной. Зависимость теплоёмкости от температуры Ср = f (T), выражается в виде степенного ряда. Например, Cp = а + в Т + с Т2 + с’/ T2 , (2.39) где а, в, с, с’ – температурные коэффициенты теплоёмкости. Отсюда, для химической реакции изменение теплоёмкости определяется следующим образом: Cp = а + в Т + с Т2 + с’/ T2 . (2.40) После подстановки уравнения (2.40) в уравнение Кирхгофа (2.36), и интегрирования в неопределённых пределах получаем: HТ = H0 + аТ + в/2 Т2 + с/3 Т3 + с’/ T. (2.41) H0 – постоянная интегрирования, которая определяется по полученному опытным путём тепловому эффекту при одной температуре. Интегрирование уравнения после подстановки (2.40 в 2.36) можно провести в интервале температур от Т1 до Т2. При этом получим следующее уравнение: HТ2 = HТ 1 + а·(Т2 – Т1) + (в/2) · (Т22 – Т21) + (с/3) · (Т32 – Т31) + с’·(1/T1 – 1/Т2). (2.42) Если Т1 = 298 К, а Т2 = Т то получаем урвавнение: HТ = H0298 + а·(Т – 298) + (в/2)·(Т2 – 2982) + (с/3)·(Т3 – 2983) + с’·(1/298 – 1/Т). (2.43) Для органических веществ это уравнение будет иметь вид HТ2 = HТ1 + а· (Т2 – Т1) + (в/2) · (Т22 – Т21) + (с/3) · (Т32 – Т31) + d/4· (Т42 – Т41). (2.44) Следует отметить, что уравнения (2.41 – 2.44) справедливы только в том интервале температур, для которого справедливы эмпирические уравнения (2.29 – 2.31) теплоёмкостей веществ, участвующих в реакции. Уравнения (2.41 – 2.44) называются интегральными уравнениями Кирхгофа в развернутом виде. 5. Обратимые и необратимые, самопроизвольные и несамопроизвольные процессы. Второй закон термодинамики, его формулировки и математическое выражение. Цикл Карно. Обратимые и необратимые процессы Все процессы, в которых один вид энергии преобразуется в другой, строго подчиняются первому закону термодинамики. Однако этот закон ничего не говорит о направлении процесса. Так первому закону не противоречит переход теплоты от горячего тела к холодному и наоборот. Однако, на опыте наблюдается только самопроизвольный переход теплоты от горячего тела к холодному. Точно также происходит диффузия молекул в направлении от более высокой концентрации к низкой. Все эти процессы протекают самопроизвольно. Такие процессы называются необратимыми или естественными. После протекания необратимого процесса систему можно вернуть в исходное состояние только путем каких-либо изменений в ней самой или окружающей среде. Во время течения процесса происходят невосполнимые потери энергии в виде теплоты, поэтому работа, произведенная системой при самопроизвольном (естественном)процессе, меньше работы, затраченной на возвращение системы в исходное состояние. Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа. Обратимыми называются процессы, которые могут идти как в прямом, так и в обратном направлениях при бесконечно малом изменении действующих на систему сил и без изменения работоспособности системы в обоих направлениях. Второй закон термодинамики, его формулировки Все процессы, происходящие в окружающем нас мире, можно разделить на три группы:
Второй закон термодинамики определяет:
Второй закон термодинамики, также как и первый, был установлен как постулат, обоснованный большим опытом, накопленным человечеством. Он формулируется по-разному. В качестве одной из формулировок принят постулат Клаузиуса (1850): - теплота не может переходить сама собой от менее нагретого тела к более нагретому; - невозможен процесс, единственным результатом которого является превращение теплоты в работу; - невозможно построить такую периодически действующую машину (вечный двигатель второго рода), все действия которой сводились бы к производству работы и соответствующему охлаждению теплового источника. В теории интегралов доказывается, что если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение является полным дифференциалом некоторой функции от параметров, определяющих состояние системы. Такой функцией является энтропия S, введенная Клаузиусом (1850). Математической записью второго закона термодинамикидля обратимых процессов является: 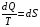 . .Цикл Карно Сущность ограничений, налагаемых вторым законом на превращение теплоты в работу, можно пояснить на примере действия идеальной машины (машина работает без трения и без потерь тепла, а под рабочим телом подразумевается идеальный газ), работающей по принципу обратимого цикла С. Карно (1824 г). Рассматриваемый цикл состоит из четырех процессов: 1) изотермического расширения; 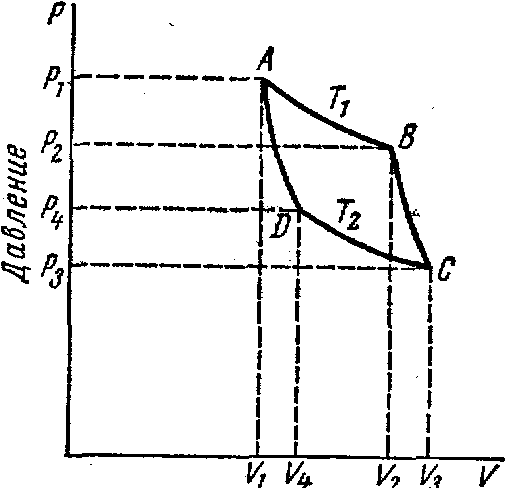 2) адиабатического расширения; 3) изотермического сжатия; 4) адиабатического сжатия газа. Все процессы проводятся обратимо, в результате чего газ возвращается в исходное состояние. Пусть количество газа равно 1-ому молю. Начальное состояние характеризуется температурой Т1, давлением p1, объемом V1 (точка А на рис.). В первом процессе газ изотермически и обратимо расширяется от объема V1 до объема V2. Допустим, что теплоотдатчик так велик, что его температура заметно не изменяется. В таком процессе газ производит работу расширения А1 цели ком за счет поглощения теплоты Q1. Тогда 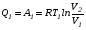 . .Прекратив в точке В подачу тепла, дадим газу адиабатически расшириться. Работа А2, совершаемая при таком расширении, происходит целиком за счет уменьшения внутренней энергии газа, т. е. понижения его температуры. Последняя падает от Т1 до Т2. Объем газа в точке С будет 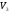 . Изменение внутренней энергии в этих условиях . Изменение внутренней энергии в этих условиях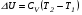 . .Работа в этом процессе в точности равна убыли внутренней энер гии 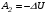 , откуда , откуда 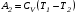 . .От точки С до точки D проводим изотермическое сжатие (теплота отводится в холодильник). При изотермическом сжатии внутренняя энергия газа не изменяется, ибо температура Т2 постоянна. Вся работа А3, затрачиваемая на сжатие, переходит в теплоту Q2, которая и отводится в холодильник. Таким образом, 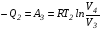 . .Последний процесс - адиабатическое сжатие газа - проведем следующим образом: отсоединим газ от теплоприемника и сожмем его до объема 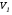 , т. е. вернем , т. е. вернем газ в исходное состояние. В этом процессе внутренняя энергия газа возрастет на величину, равную затрачен ной работе сжатия А4: 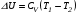 ; ; 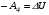 , ,т.е. 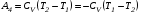 . .Так как процесс в целом является круговым, то внутренняя энер гия газа в конечном состоянии равна таковой в начальном состоянии, и общее количество теплоты, полученное газом, равно общему количеству произведенной им работы 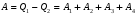 . . А2 и А4 равны по абсолютному значению, но противоположны по знаку. Учитывая это, получим: 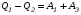 . Подставив вместо А1 и А3 соответствующие им значения, получим: . Подставив вместо А1 и А3 соответствующие им значения, получим: 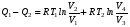 или или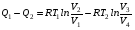 . . Используя уравнение адиабаты 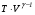 = соnst, где = соnst, где 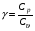 , можно доказать, что , можно доказать, что 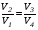 , ,тогда 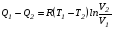 . .Разделив левую и правую части этого равенства на уравнение (2.1), будем иметь: 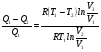 ; ; 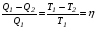 , ,где η – коэффициент полезного действия (К.П.Д.) тепловой машины. Отсюда видно, что коэффициент полезного действия цикла 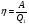 зависит только от разности температур нагревателя и холодильника. Так как Т2<Т1, то зависит только от разности температур нагревателя и холодильника. Так как Т2<Т1, то 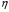 <1. Следовательно, даже в идеальном случае существует предел превращения теплоты в работу. <1. Следовательно, даже в идеальном случае существует предел превращения теплоты в работу.Можно доказать, что тепловая машина, работающая по любому реальному циклу, будет иметь коэффициент полезного действия меньше, чем работающая по циклу Карно. |
