Физическая химия (1-15 вопросы). Дисциплина Физическая химия
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
рБудем считать, что поршень движется без трения. Зная, что сила, под действием которой смещается поршень, будет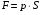 . .Тогда работа будет равна: 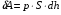 . .Так как произведение 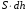 - это изменение объема - это изменение объема 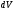 , то , то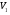 до до 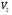 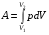 . .Четыре частных случая: 1) Изобарный процесс. р=const. Тогда интегрирование приводит к выражению: p p 0  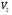 E FF ДНF 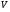 C Gт. е. работа изобарного расширения газа равна произведению давления на увеличение объема.На графике р - V эта работа выражается площадью прямоугольника 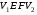 . . Для 1-го моля воспользуемся уравнением Клапейрона - Менделеева 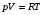 . Тогда можно записать: . Тогда можно записать: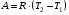 . .2) Изотермический процесс. Т=const. Из уравнения Клапейрона - Менделеева 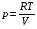 Подставив которое в выражение 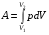 , получим: , получим: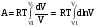 . .В результате интегрирования получим: 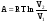 . .На графике р-V эта работа выражается площадьюV1EF/V2. Зная из закона Бойля-Мариотта что 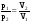 , получим: , получим: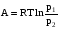 . .3) Адиабатное расширение происходит при одновременном изменении температуры и давления, оно отвечает условию: dQ=0. Газ не получает теплоту, поэтому работа расширения газа происходит за счет внутренней энергии. При этом газ должен охлаждаться. Внутренняя энергия зависит только от температуры. 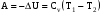 . .На графике p-Vэто площадьV1EF//V2.. 4) Изохорный процесс. V= const, dV = 0, А = 0. Работа расширения идеального газа. Учитывая выведенное раннее разделение полной работы процесса на работу расширения и полезную работу (см. 1.6 и 1.10), математическое выражение первого закона термодинамики (2.3) можно представить в виде: q = dU + W’+ pdV. (2.5) Равенство (2.5) может служить основой для расчётов тепловых эффектов (теплот) любых процессов. Для упрощения будем считать, что рассматриваемая система не производит других видов работы, кроме работы расширения, т. е. W’ = 0. Тогда уравнение первого закона термодинамики приобретёт вид: q = dU + pdV. (2.6) При изобарном процесе (р = const) давление можно ввести под знак дифференциала и, следовательно, рdV = d (рV). Таким образом, правая часть равенства (2.6) состоит из суммы полных дифференциалов, которая, как известно из математики, также является полным дифференциалом некоторой функции Н – энтальпии: q = dU + d (pV) = d (U + pV) = dH. (2.7) Таким образом, теплота изобарного процесса оказывается равной приращению функции состояния энтальпии (Н), что позволяет перейти от бесконечно малого приращения к конечному. 2 2 qр = qp = dH = H2 – H1 = H. (2.8) 1 1 Энтальпия является функцией состояния и связана с внутренней энергией уравнением: Н = U + pV. (2.9) Как следует из равенства (2.8) приращение энтальпии Н равно теплоте изобарного процесса, т. е. для определения теплоты изобарного процесса достаточно знать значения энтальпии системы в её начальном и конечном состоянии. Наиболее простой путь определения энтальпии основан на измерении теплоёмкости тел при постоянном давлении. Действительно, теплоёмкость есть отношение количества сообщённой телу теплоты к приращению температуры тела: C = 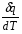 . (2.10 ) . (2.10 )Для случая Р = const имеем: Cp = 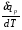 = = 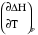 . (2.11) . (2.11)Состояние тела может быть однозначно задано двумя параметрами, например, давлением и температурой. Следовательно, функция состояния Н = f (Р, T). Н зависит от двух переменных, и её полный дифференциал имеет вид: dH = 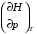 dp + dp + 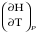 dT. (2.12) dT. (2.12)Для изобарных процессов первый член правой части равен нулю, т. к. dp = 0, а второй, согласно (2.11) содержит величину изобарной теплоёмкости (Ср). Отсюда, сделав соответствующую замену, и интегрируя уравнение: dH = Cp dT получаем: qP = H = Cp(T2 – T1). (2.13) При изохорном процессе V = const, dV = 0 и равенство (2.6) примет вид: qv = dU. (2.14) После интегрирования уравнения (2.14) от состояния “1” до состояния “2” получаем для конечного процесса: qv = U2 – U1 = U. (2.15) Т. е. теплота изохорного процесса равна приращению внутренней энергии. Аналогично энтальпии, внутренняя энергия может быть найдена по теплоёмкостям, измеренным при постоянном объёме. Вывод уравнений аналогичен вышеприведённому. dU = 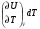 + + 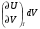 , ,Cv = 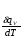 = = 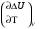 , (2.16) , (2.16)2 dU = Cv dT, 1 Тогда согласно (2,14) qV = U = CV(T2 – T1). (2.17) 2. Теплоемкость. Виды теплоемкости. Связь между средней и истинной теплоемкостью. Теплоемкость при постоянном давлении и объеме и связь между ними. Температурная зависимость теплоемкости от температуры. Теплоемкость Теплоемкостью называется количество теплоты, необходимое для нагревания данной массы вещества на один градус. Различают удельную и мольную теплоемкости. Удельной теплоемкостью называется количество теплоты, необходимое для нагревания 1 г вещества на один градус, а мольной теплоемкостью - 1 моля вещества на один градус. Различают истинную и среднюю теплоемкости. Истинной мольной теплоемкостью называют отношение бесконечно малого количества теплоты, которое нужно подвести к 1 молю вещества, к бесконечно малому приращению температуры, которое при этом наблюдается: 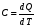 где С- мольная теплоемкость, Дж /моль·град. Средней мольной теплоемкостью в пределах температур от Т1 до Т2 называют отношение количества теплоты, подведенное к 1 молю вещества, к разности температур: 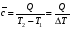 Связь между истинной и средней теплоемкостью: 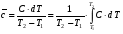 Атомной теплоемкостью называется количество теплоты, необходимое для нагревания 1 кг-атома вещества на 1градус [Дж/кг- атом·град]. Иногда теплоемкость относят к единице объема, тогда она называется объемной. Все перечисленные теплоёмкости связаны друг с другом соотношениями: Смол = Суд·М (для любых веществ), Сат = Суд ·А (для металлов), Соб = Смол/22,4 (для газов), Соб = Суд ·, (для жидкостей и твердых тел), где М –молярная масса, кг/кмоль; А – атомная масса, кг/кг-атом; -плотность вещества, кг/м 3. Теплоемкость при постоянном давлении и объеме и связь между ними. Теплоёмкость не является функцией состояния, она определяется характером процесса. В зависимости от условий проведения процесса различают изохорную (Сv) и изобарную (Ср) теплоёмкости. Для идеального газа: Сν = 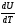 ; Ср = ; Ср = 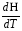 . .Для других систем используются частные производные: Сν = 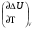 ; Ср = ; Ср = 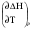 . .Связь между Ср и Сv определяется уравнением Р. Майера. Ср - Сν = R. где R – универсальная газовая постоянная. В теплотехнике широко применяется отношение теплоемкостей k = Ср/Сν, которое носит название коэффициента Пуассона (показателя адиабаты). Температурная зависимость теплоемкости от температуры. Температура значительно влияет на величину теплоёмкости и это влияние различно в различных температурных интервалах. Температурную теплоёмкость можно схематично рассмотреть на графике. C=aT3 Cν=3 Cp=5 C=Const C=6,2+6,4 C=α+βT+γT2 T 00K Tкомн Tпл Tкип Теплоемкость C Рис. Зависимость теплоёмкости от температуры. Ткомн – стандартная температура, 298 К. I область. (0К–298К) зависимость описывается уравнением Дебая: С = аТ3 При Т0=298К теплоёмкость определяется правилом Дюлонга-Пти: Атомная теплоёмкость элементов в твёрдом состоянии есть величина приблизительно одинаковая для всех элементов и в среднем равная Сат = 6,2 6,4 кал/ г-атомград. или Сат = 25,9 26,7 Дж/г-атомград. Для молекул Нейманом и Коппом сформулировано правило аддитивности: молярная теплоёмкость равна сумме теплоёмкости атомов, входящих в состав вещества. См = Сат. См = М·Суд = n·(25,9 26,7) Дж/ моль·град. II область: (298 К – Тпл) Зависимость теплоёмкости от температуры выражается степенным рядом: Ср = а + вТ + сТ2; Ср = а + вТ + с’ Т-2; Ср = а + вТ + сТ2 + dТ3. где а, в, d, с, с’ – эмпирические температурные коэффициенты теплоёмкости. III область: (Тпл-Ткип) Для жидкого состояния теплоёмкость характеризуется в целом величиной меньшей, чем для твёрдого состояния и остаётся величиной постоянной во всем интервале температур. IV область: (выше Ткип) В этом случае теплоёмкость газообразного состояния вещества также остаётся величиной постоянной и ещё меньшей, чем в жидком состоянии. Для одноатомных металлов в газообразном состоянии теплоёмкость определяется величинами: Сv = 3 кал / г-атомград = 12,54 Дж/ г-атомград, Ср = 5 кал / г-атомград = 20,9 Дж/ г-атомград. 3. Закон Гесса и следствия из него. Применение первого закона термодинамики к химическим процессам. Связь между qp и qv. Расчет тепловых эффектов химических реакций по теплотам образования и теплотам сгорания веществ (на примере реакции). Закон Гесса В 1836 г. Г. И. Гесс открыл основной закон термохимии, который является частным случаем первого закона термодинамики применительно к химическим реакциям, протекающим в изохорных или изобарных условиях. Закон Гесса устанавливает: если из данных исходных веществ можно получить заданные конечные вещества различными путями, то суммарная теплота на одном каком-нибудь пути равна суммарной теплоте процесса на другом пути, т.е. тепловой эффект химических реакций зависит только от начального и конечного состояния системы, но не зависит от пути перехода. Из закона Гесса выводится ряд следствий: I следствие: Тепловой эффект разложения какого-либо соединения равен по величине, но противоположен по знаку тепловому эффекту образования этого соединения. Н разл. = - Н обр. 6Сграфит + 3Н2 (газ) = С6Н6 (жид.) + 49 кДж Теплотой разложения химического соединения называется тепловой эффект разложения одного моля сложного вещества на простые вещества в их устойчивых соединениях при стандартных условиях С6Н6 6С + 3Н2 - 49 кДж II следствие: Тепловой эффект химической реакции равен разности алгебраических сумм теплот образования продуктов реакции и исходных веществ. Так для реакции общего типа: аА + bB сС + dД Тепловой эффект рассчитывается по уравнению: Нхр = [с Нобр. (С) + d Нобр. (D)] - [a Нобр. (A) + b Нобр. (B)]. Если энтальпия (теплота образования) измеряется при стандартных условиях: Р = 101 325 Па и Т = 25 0С = 298 0К, то обозначается Н0298. III следствие: Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных веществ и продуктов реакции. Для вышеуказанной реакции общего типа тепловой эффект равен: Нхр = [а Нсгор. (А) + в Нсгор. (В)] - [с Нсгор. (С) + d Нсгор. (D)]. 2С6Н6 + 15О2 12 СО2 + 6Н2О С6Н6 + 15/2 О2 6 СО2 + 3Н2О + Нсгор. Теплоту сгорания с точностью до (0,01 %) можно определить калориметрическим методом или рассчитать по формуле Д. П. Коновалова: Qсг. = 204,2 n + 44m + x, где n – число атомов кислорода необходимых для полного сгорания 1 моля вещества; m – число молей воды; x – термическая характеристика, является функцией связей или групп атомов. IV следствие: Если две реакции имеют одинаковое начальное состояние, но различное конечное, то разность их тепловых эффектов равна тепловому эффекту перехода из одного конечного состояния в другое. С + 1/2 О2 СО - Н1 С + О2 СО2 - Н Для СО + 1/2 О2 СО2 - Н2 Н2 = Н - Н1 V следствие: Если две реакции из различных начальных состояний переходят к одному конечному состоянию, то разность их тепловых эффектов равна тепловому эффекту перехода одного начального состояния в другое. С + О2 СО2 - Н СО + 1/2 О2 СО2 - Н2 С + 1/2 О2 СО - Н1 Н1 = Н - Н2 Применение первого закона термодинамики к химическим процессам. С + О2 СО + ½ О2 СО2  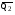 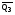 Рис. Применение закона Гесса к вычислению теплового эффекта образования окиси углерода Закон Гесса незаменим для расчета тех тепловых эффектов, которые не могут быть измерены калориметрическим путем. Например, при реакции С + О2в качестве конечного продукта образуется СО2, а при неполном сгорании – СО и СО2. Вследствие протекания реакции в двух направлениях прямое определение теплоты образования СО неосуществимо. Для нахождения этого теплового эффекта можно воспользоваться законом Гесса. Образование двуокиси углерода может быть осуществлено двумя путями (рис.). 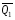 и и 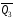 легко определяются опытным путем, а легко определяются опытным путем, а 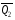 - тепловой эффект образования СО – находят при помощи закона Гесса - тепловой эффект образования СО – находят при помощи закона Гесса 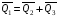 , ,откуда 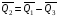 . .Связь между qp и qv. Согласно принятой в термодинамике системе знаков отрицательному значению Qυ соответствует выделение теплоты (экзотермические реакции), а положительному – поглощение (эндотермические реакции). В термохимии, в силу исторических традиций, часто применяется термохимическая система знаков для теплоты реакции (и теплоты растворения). Положительной считается теплота, выделившаяся в результате реакции, а отрицательной – поглощенная теплота. Будем обозначать термохимическую теплоту 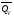 при условии, что при условии, что 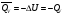 . .Стехиометрические уравнения химической реакции, содержащие в правой части тепловой эффект 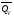 (или (или 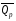 при р = const), называются термохимическими. при р = const), называются термохимическими.Кроме указания на агрегатное или модификационное состояние участников реакции, должны указываться условия проведения реакции, от которых также зависит тепловой эффект реакции. В частности, тепловой эффект 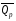 больше теплового эффекта больше теплового эффекта 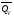 на величину работы расширения А = рΔu = Δ νRT газообразных участников реакции: на величину работы расширения А = рΔu = Δ νRT газообразных участников реакции: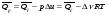 , ,где Δν- прирост числа молей газообразных веществ, рассчитанный по стехиометрическому уравнению. Расчет тепловых эффектов химических реакций по теплотам образования и теплотам сгорания веществ (на примере реакции). Измерение тепловых эффектов возможно при соблюдении двух условий: 1) когда в системе протекает только одна реакция; 2) реакция протекает до конца достаточно быстро, так что теплота за время ее измерения не успевает рассеиваться в окружающую среду. При расчетах тепловых эффектов химических реакций на основе закона Гесса особое значение имеют два вида тепловых эффектов – теплота образования и теплота сгорания. Теплотой образования называется тепловой эффект реакции образования 1 моль данного соединения из простых веществ, отвечающих наиболее устойчивому состоянию элементов при данной температуре. Например, теплота образования СаСО3 равна тепловому эффекту реакции образования карбоната кальция в данной его кристаллической модификации из металлического кальция, углерода (графит) и газообразного кислорода: 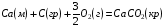 . .Теплоту образования относят к одному молю соединения при температуре 250С и называют стандартной теплотой образования 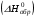 . Тепловой эффект любой химической реакции можно легко рассчитать, если известны теплоты образования всех веществ, участвующих в реакции. Из закона Гесса следует, что тепловой эффект реакции равен разности между теплотами образования всех веществ, указанных в правой части уравнения, и теплотами образования всех веществ, указанных в левой части уравнения реакции, взятых с соответствующими стехиометрическими коэффициентами. . Тепловой эффект любой химической реакции можно легко рассчитать, если известны теплоты образования всех веществ, участвующих в реакции. Из закона Гесса следует, что тепловой эффект реакции равен разности между теплотами образования всех веществ, указанных в правой части уравнения, и теплотами образования всех веществ, указанных в левой части уравнения реакции, взятых с соответствующими стехиометрическими коэффициентами.Например, дана реакция bB + dD = gG + rR +  дж. дж.Обозначим теплоты образования соответственно через 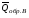 , , 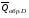 , , 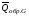 , , 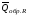 . .Тепловой эффект реакции 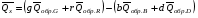 , ,или в общем случае 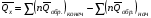 ; ;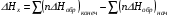 . .Теплотой сгорания называется тепловой эффект реакции окисления 1 моль данного соединения кислородом с образованием высших окислов соответствующих элементов. Для органических соединений теплотой сгорания называется тепловой эффект реакции полного сгорания данного соединения до углекислого газа, водяных паров и других продуктов. Отнесенная к 250С, теплота сгорания называется стандартной теплотой сгорания 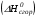 . .Если известны теплоты сгорания всех веществ, участвующих в реакции, то можно рассчитать тепловой эффект самой реакции. Из закона Гесса следует, что тепловой эффект реакции равен разности между теплотами сгорания веществ, указанных в левой части уравнения, и теплотами сгорания веществ, указанных в правой части уравнения, взятых с соответствующими стехиометрическими коэффициентами. Для реакции bB + dD = gG + rR + 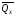 , если теплоты сгорания обозначим соответственно , если теплоты сгорания обозначим соответственно 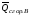 , , 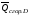 , , 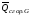 , , 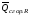 , ,тепловой эффект 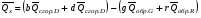 . .В общем виде 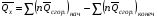 ; ;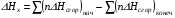 . .Заметим, что в обоих случаях теплоты образования и сгорания должны определяться в одинаковых условиях – или в изобарных, или изохорных. Изобарные и изохорные стандартные теплоты образования и сгорания многих соединений можно найти в справочниках. Для приближенного расчета тепловых эффектов существует целый ряд эмпирических закономерностей. Например, для расчета теплот сгорания органических веществ применяется приближенная формула, предложенная Д. П. Коноваловым 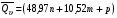 ккал/моль, ккал/моль,где n – число атомов кислорода, требующихся для полного сгорания данного вещества; m – число молей образующейся жидкой воды; р - поправочная величина, названная Коноваловым термической характеристикой. Постоянный коэффициент 48,97 выражает теплоту полного сгорания угля в расчете на один грамм-атом кислорода, а коэффициент 10,52 – теплоту конденсации образующихся водяных паров. Для соединения, имеющего эмпирическую формулу СхНуОz, 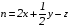 и и 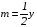 . .Для всех предельных органических соединений р = 0. Для непредельных соединений р ≠ 0. Значение этой величины является постоянным для всех членов данного гомологического ряда и растет с повышением непредельности; например, для соединений ацетиленового ряда р = 51. |
