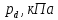Гидромеханика Курсовая работа. Гидромеханика. Курсовая работа Курсовая работа допущена к защите защищена с оценкой 202 г. Руководитель
 Скачать 4.6 Mb. Скачать 4.6 Mb.
|
|
2. Исходные данные и принятые положения: Диаметр понтона:D= 8 м. Длина понтона: L=44 м. Плотность воды: р = 1,025 т/мз Скорость набегающего потока жидкости: Vо = 12 м/с Жидкость безграничная и идеальная. Примем, что понтон - часть цилиндра бесконечного размаха, т.е. понтон обтекается таким же образом, как и цилиндр бесконечного размаха. Используем в задаче декартову систему координат с центром в точке пересечения осей понтона. При этом оси Y и X лежат в продольно вертикальной плоскости симметрии понтона, ось Y направлена вертикально, X ось - горизонтальна. Ось Z - горизонтальна и направлена перпендикулярно диаметральной плоскости понтона. Также будем использовать цилиндрическую систему координат, которая определяется величинами rо - расстояние от начала координат до рассматриваемой точки, θ - угол между зафиксированным, горизонтально направленным лучом и отрезком, соединяющим точку и начало координат. 3. Определение потенциала скоростей и функции тока: Потенциал скорости потока, который набегает на цилиндр, можно представить в виде суммы потенциалов скоростей равномерного потока и диполя, ось которого совпадает с осью цилиндра. Функцию тока также можно представить в виде суммы функций тока равномерного потока и диполя: φ = 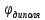 + +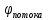 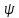 = = 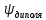 + +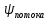 Потенциал скоростей и функцию тока в цилиндрической системе координат, можно выразить в следующем виде: φ = ( 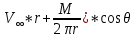 (4.1) (4.1)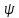 = ( = ( 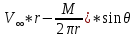 (4.2) (4.2)где 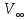 - скорость потока на бесконечном удалении от цилиндра - скорость потока на бесконечном удалении от цилиндра М - момент диполя, определяемый по формуле М = 2*π* 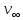 * *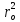 ro- радиус цилиндра, равный ro = D/2 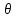 - угол между радиус-вектором, соединяющим рассматриваемую точку, и началом координат, с горизонтально направленным, зафиксированным лучом. - угол между радиус-вектором, соединяющим рассматриваемую точку, и началом координат, с горизонтально направленным, зафиксированным лучом.Подставив (4.3) в (4.1), (4.2), получим: φ = 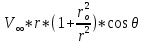 (4.4) (4.4)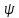 = = 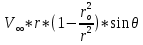 (4.5) (4.5)4. Определение значений скорости потока: Скорость потока можно представить, как сумма радиальной Vr и окружной 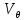 скоростей: скоростей:V = 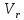 + +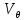 (4.6) (4.6)Или скорость потока можно представить так: V = 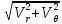 (4.7) (4.7)Определим составляющие формулы (4.7): 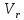 = = 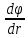 = = 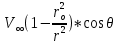 (4.8) (4.8)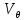 = = 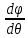 * * 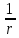 = = 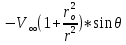 (4.9) (4.9)5. Построение картины линий течения тока для поперечного сечения цилиндра: В общем случае, уравнение семейства линий тока имеет вид: 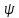 = C (4.10) = C (4.10)где С - константа, описывающая местоположение всех точек определенной линии тока в пространстве. В данном случае, уравнение линии тока для поперечного сечения цилиндра имеет следующий вид: 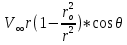 = C (4.11) = C (4.11)По условию задачи промежуток между двумя соседними линиями тока одинаков и равен: 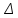 C = C = 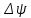 = = 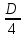 * *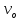 (4.12) (4.12)Подставляя данные значения в (4.11), получим 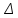 C = C = 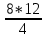 = 24 м^2/с = 24 м^2/сЗададим начальное значение величины С= 0, и будем изменять эту величину с шагом 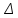 C = 24 м^2/с. C = 24 м^2/с.В уравнении функции тока (4.11) имеются 2 переменные 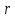 и и 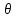 . Чтобы построить линии тока, будем задавать переменную . Чтобы построить линии тока, будем задавать переменную 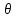 с шагом в 10 градусов. Для построения линии тока, необходимо разрешить уравнение (4.11) относительно переменной с шагом в 10 градусов. Для построения линии тока, необходимо разрешить уравнение (4.11) относительно переменной 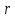 . В итоге получим: . В итоге получим: 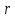 = = 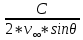 + + 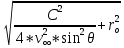 (4.13) (4.13)Так как линии тока симметричны относительно осей oY и оХ, будем считать координаты точек линий тока лишь для первого квадранта. Координаты представлены в таблице №1. Таблица№1
По найденным координатам построим картину линий тока (рис.4.2) 6. Определение давления на поверхности цилиндра. Построение эпюры гидродинамических давлений на поверхности цилиндра. Гидродинамическое давление в условиях данной задачи определяется формулой: 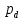 = = 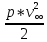 * (1-4* * (1-4*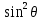 ) (4.14) ) (4.14)где 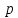 - плотность жидкости - плотность жидкостиТак как гидродинамическое давление симметрично относительно осей оY и оХ, то рассчитаем его лишь для первого квадранта. Результаты расчётов представлены в таблице №2. Таблица №2
По данным таблицы №2 построим эпюру гидродинамических давлений на поверхности цилиндра (рис.4.3). 7. Построение эпюры скоростей в точках оси oY. В точках оси оY угол 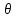 = ±90°, следовательно, sin = ±90°, следовательно, sin 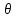 = ±1, a cos = ±1, a cos 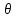 = 0. С учётом этого и выражений (4.7),(4.8),(4.9) выражение скорости в точках оси оY примет вид: = 0. С учётом этого и выражений (4.7),(4.8),(4.9) выражение скорости в точках оси оY примет вид:Vr = 0 (так как cos 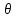 = 0) = 0)V = 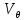 = = 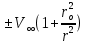 (4.15) (4.15)Результаты расчетов скоростей представим в таблице №3: Таблица №3
По данным таблицы №3 построим эпюру скоростей (рис.4.4). |