Гидромеханика Курсовая работа. Гидромеханика. Курсовая работа Курсовая работа допущена к защите защищена с оценкой 202 г. Руководитель
 Скачать 4.6 Mb. Скачать 4.6 Mb.
|
|
Картина линий тока 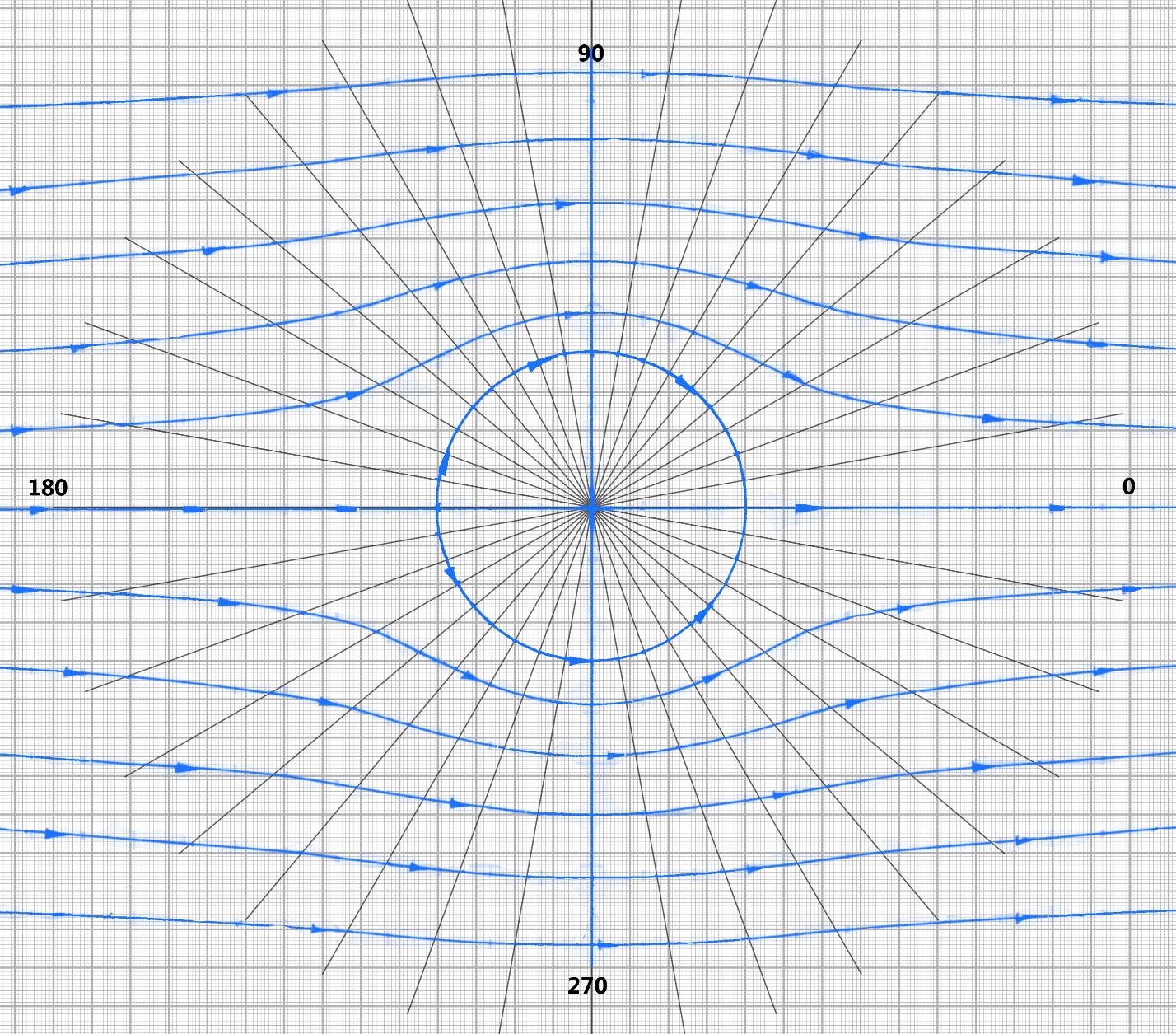 Рис. 4.2 Эпюра гидродинамических давлений 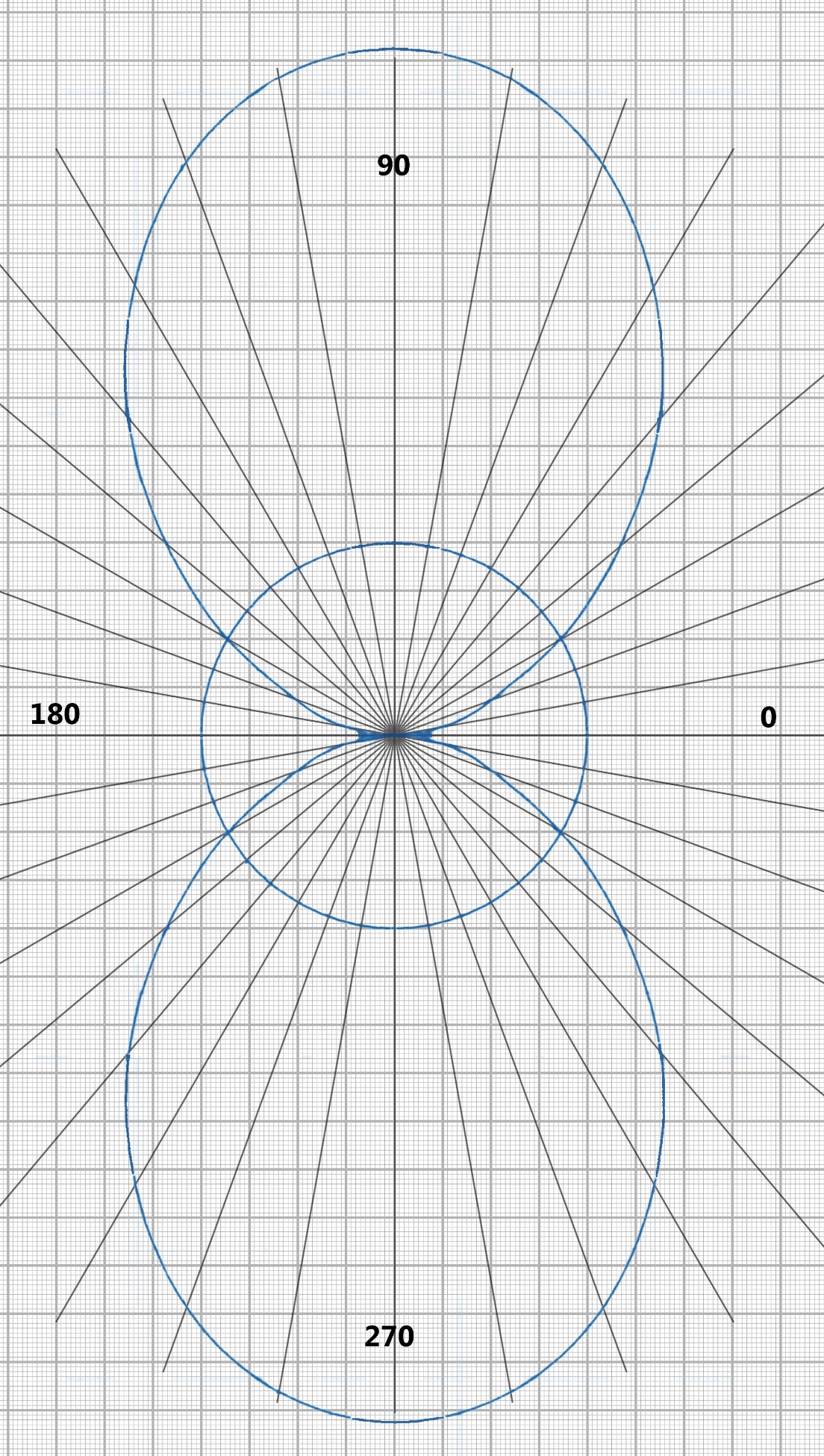 Рис. 4.3 Эпюра скоростей 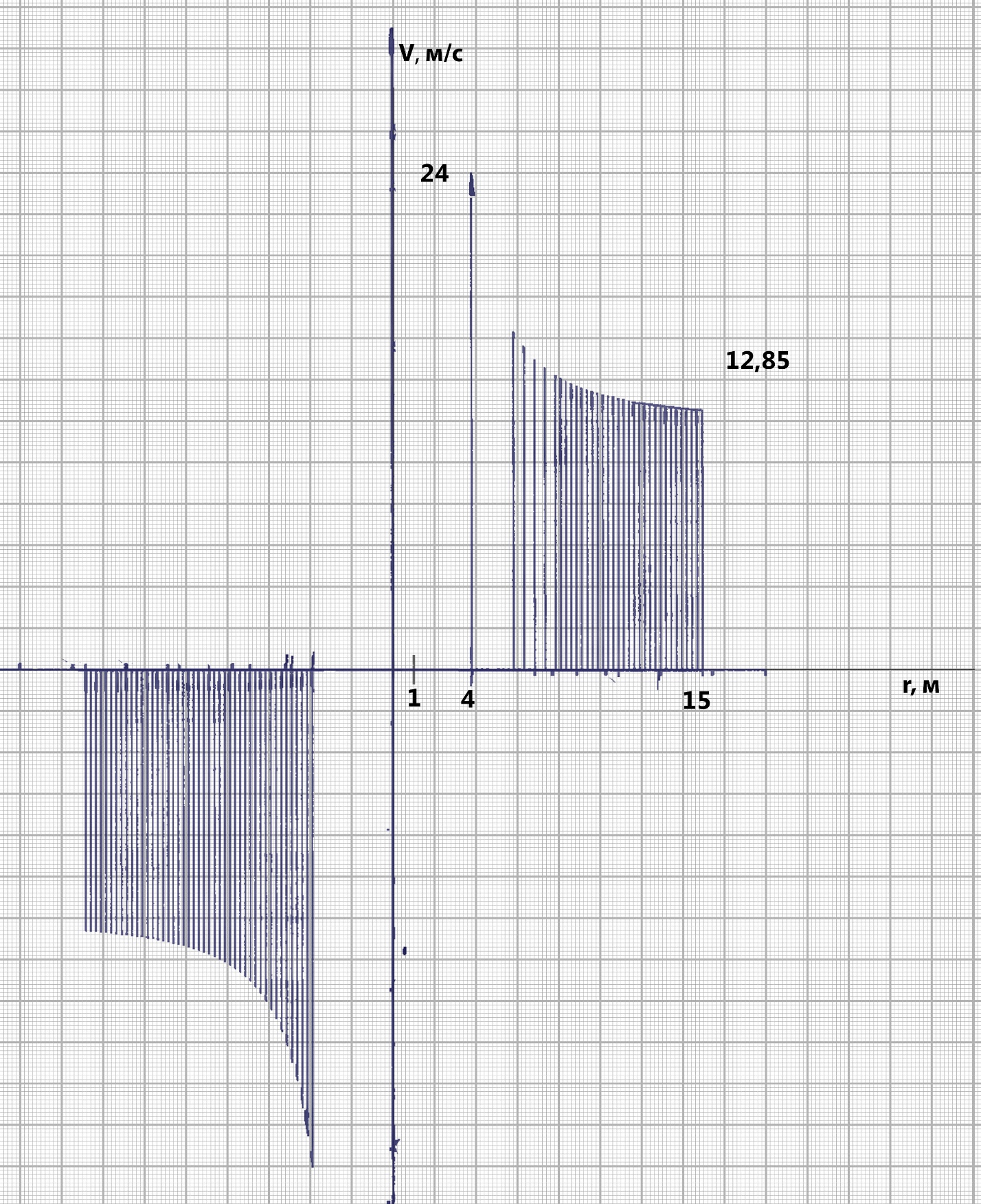 Рис. 4.4 Задача 5 1. Содержание задачи. На описанное в задаче № 4 течение наложить плоский вихрь интенсивностью I (см. рис. 5.1). Построить эпюру гидродинамических давлений на поверхности цилиндра и график изменения скорости потока вдоль оси Оу. Определить положение критических точек и найти действующую на цилиндр подъёмную силу. 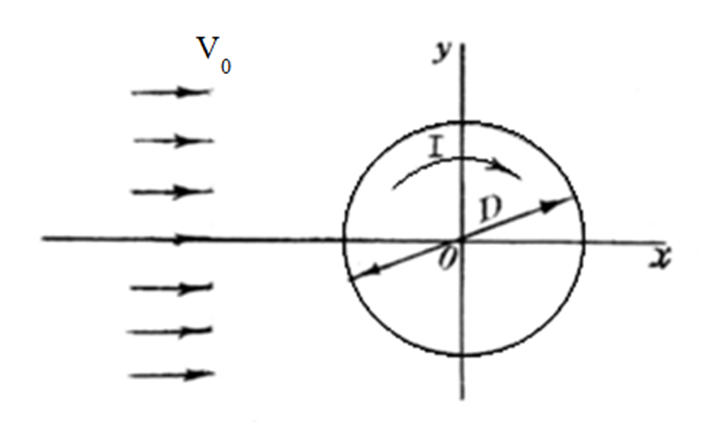 Рис.5.1 2. Исходные данные. Диаметр понтона: D= 8 м. Длина понтона: L=44 м. Плотность воды: р = 1,025 т/ м^3 Скорость набегающего потока жидкости: 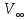 = 12 м/с = 12 м/с Интенсивность вихря определяется из выражения 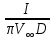 = -0,9 м2/с = -0,9 м2/сВ задаче используется цилиндрическая система координат, с началом координат, расположенным на оси понтона, осью oZ, совпадающей также с осью понтона, и определяемая величинами r - расстоянием от начала координат до рассматриваемой точки, 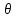 - углом между осью отсчета, направленной по направлению потока и отрезком, соединяющим точку и начало координат. Подъемную силу Ry действующую на цилиндр, можно определить по формуле Жуковского, полагая, что наш цилиндр - часть цилиндра бесконечной длины. - углом между осью отсчета, направленной по направлению потока и отрезком, соединяющим точку и начало координат. Подъемную силу Ry действующую на цилиндр, можно определить по формуле Жуковского, полагая, что наш цилиндр - часть цилиндра бесконечной длины.3. Определение давления на поверхности цилиндра. Построение эпюры гидродинамических давлений на поверхности цилиндра. Воспользуемся формулой для гидродинамического давления на поверхности кругового цилиндра при циркуляционном обтекании: pд = 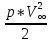 *(1 - *(1 -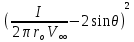 ) (5.1) ) (5.1),где p - плотность жидкости; 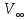 - скорость потока жидкости на бесконечном удалении от понтона; - скорость потока жидкости на бесконечном удалении от понтона; ro - радиус понтона, равный половине диаметра понтона, т.е. ro =D/2 = 8/2 = 4 м 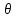 - угол между радиус-вектором, соединяющим рассматриваемую точку на поверхности понтона и начало системы координат, и осью оХ; - угол между радиус-вектором, соединяющим рассматриваемую точку на поверхности понтона и начало системы координат, и осью оХ;I - интенсивность вихря, равная I = 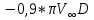 = -271.29 м^2/с (5.2) = -271.29 м^2/с (5.2)Распределение гидродинамического давления будет симметричным относительно оси oY, поэтому рассчитаем его для первого и четвертого квадрантов. Результаты расчетов представлены в таблице 1. Таблица №1
Эпюра распределения гидродинамического давления по поверхности цилиндра представлена на рисунке 5.2 4. Построение эпюры скоростей в точках оси oY. Полная скорость (V) определяется двумя составляющими - радиальной скоростью 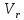 и окружной скоростью и окружной скоростью 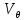 , формулы для которых соответственно имеют вид: , формулы для которых соответственно имеют вид:V = 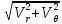 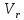 = = 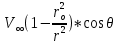 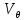 = = 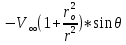 + + 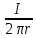 В точках оси oY 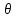 = ±90° и cos = ±90° и cos 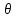 = 0, следовательно Vr=0 = 0, следовательно Vr=0Тогда выражение для нахождения полной скорости приобретает вид: V = 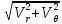 = = 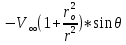 + + 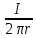 (5.3) (5.3)Следовательно, если в 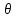 = 90°, то скорость определяем по формуле = 90°, то скорость определяем по формулеV = 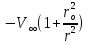 + + 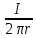 (5.4) (5.4)Если же 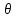 = -90°, то пользуемся следующей формулой = -90°, то пользуемся следующей формулойV = 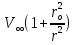 + + 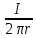 (5.5) (5.5)Подставляя различные значения r в формулы (5.4) и (5.5), получим соответствующие значения скорости в точках оси oY. Результаты запишем в таблицу 2. Таблица №2
Эпюра скоростей изображена на рисунке 5.3 5. Определение положений критических точек на поверхности цилиндра. Критические точки определим из условий, что скорость в них равна 0(V=0) и r=r0. Подставляя эти условия в уравнение скорости (5.3), получим: 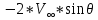 + + 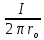 = 0 или = 0 или 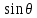 = = 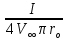 Следовательно: sin 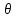 = -0,34 (5.6) = -0,34 (5.6)Откуда: 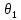 = arcsin (-0,55) = -19.88° = arcsin (-0,55) = -19.88°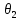 = π – arcsin(-0,55)= -160,12° = π – arcsin(-0,55)= -160,12°6. Определение подъемной силы, действующей на цилиндр. Подъемную силу, действующую на цилиндр, определим по формуле Жуковского: 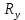 = -pIL = -pIL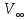 Где I- интенсивность вихря; L - длина понтона; p - плотность жидкости;  - скорость потока жидкости; - скорость потока жидкости; Ry = -1.025 * (-271.29) * 44 * 12 = 146822.14 кН = 146,8 МН Ответ:  = arcsin (-0,55) = -19.88° = arcsin (-0,55) = -19.88° = π – arcsin (-0,55) = -160,12° = π – arcsin (-0,55) = -160,12°Ry = 146,8 МН Эпюра гидродинамических давлений 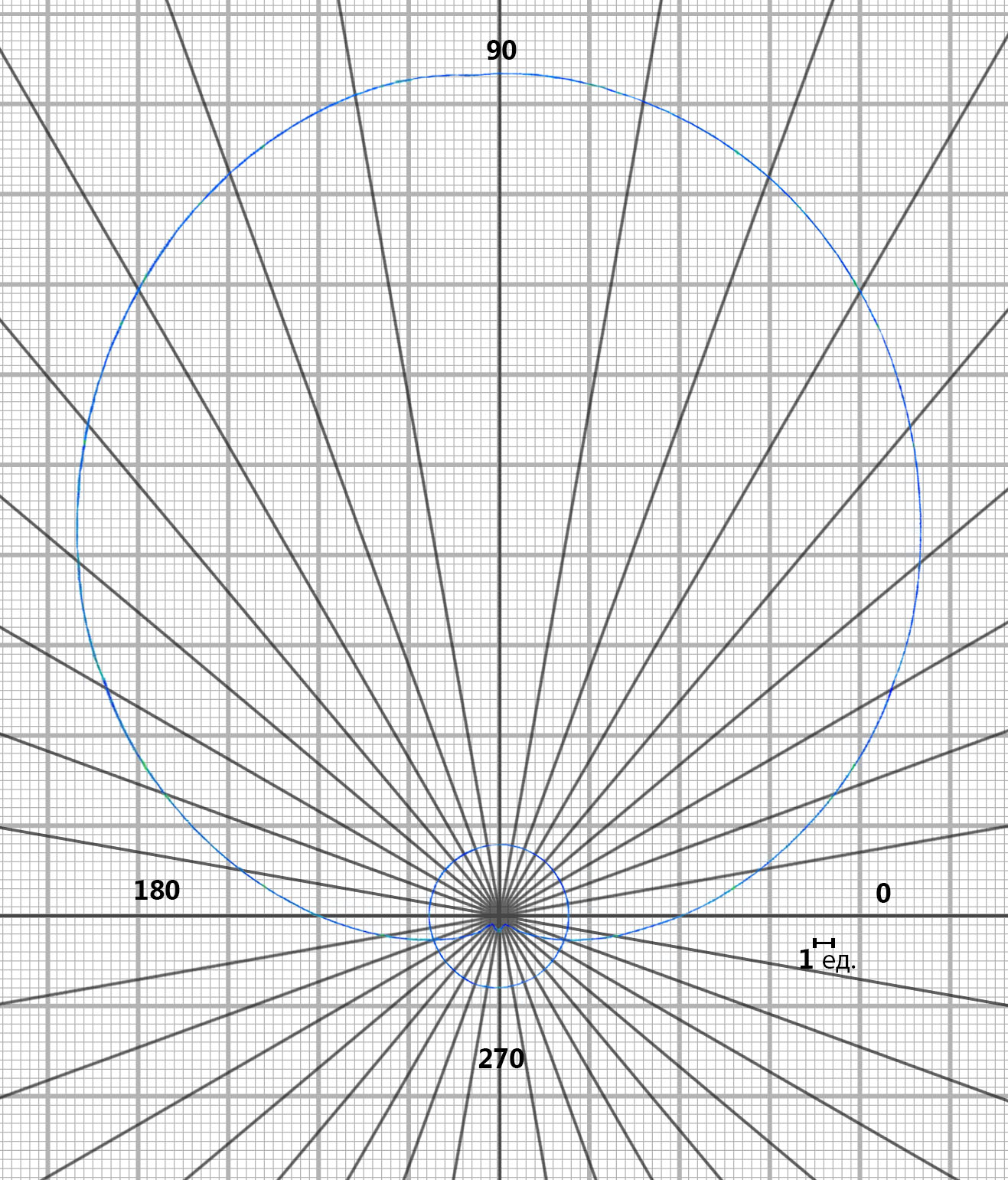 Рис. 5.2 Эпюра скоростей 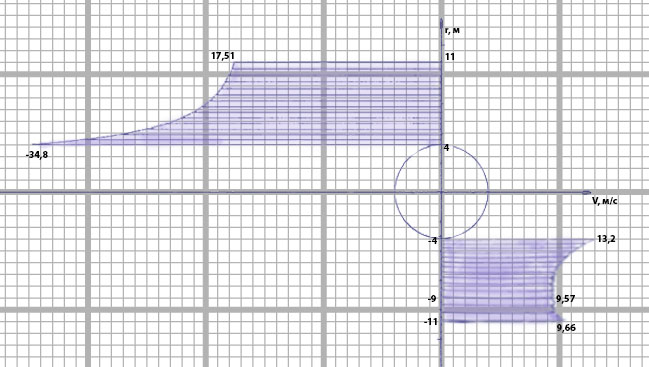 Рис. 5.3 Задача №6 1. Содержание задачи Закреплённый на дне водоёма глубиной Н понтон освобождается от удерживающих его связей и всплывает. Найти зависимость скорости его всплытия от времени Vo(t), определить время всплытия до момента соприкосновения его со свободной поверхностью и скорость в этот момент. 2. Исходные данные и принятые положения Длина понтона: L = 44 м. Диаметр понтона: D = 8 м. Глубина водоема: Н= 30 м. Плотность воды: р = 1025 кг/м^3 Ускорение свободного падения: g = 9,81 м/сек^2 В работе приняты следующие допущения: 1. Жидкость безгранична. 2. Жидкость считаем идеальной. 3. Понтон является частью цилиндра бесконечного размаха. В работе принята декартова система координат с началом отсчета в верхней точке понтона в момент его отрыва от грунта (причём с понтоном система координат не связана). При этом ось Z направлена вдоль оси понтона, ось X горизонтальна, а ось Y направлена вертикально вверх (см. рис. 6.1). 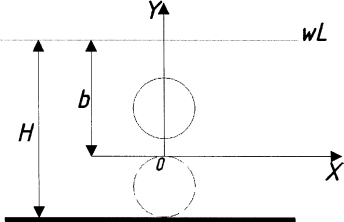 Рис. 6.1 3. Составление уравнения движения понтона. Введем новую величину - b: расстояние от верхней точки понтона, лежащего на дне цилиндра, до свободной поверхности. b=H-D (6.1) где Н - глубина водоёма, D - диаметр понтона, b= 30 – 8 = 22 м. Таким образом, начало координат будет расположено на расстоянии 22 м. от свободной поверхности воды. Понтон всплывает вертикально вверх, так как силы, действующие на его боковые стороны, взаимно уравновешиваются в силу его симметрии. Следовательно, все силы, действующие на цилиндр во время его подъема, будут направлены вдоль оси Y. Составим уравнение движения цилиндра, учитывая, что положительное направление оси Y - вертикально вверх. 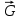 + + 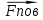 = m* = m* 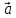 (6.2) (6.2)где 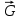 - сила тяжести, действующая на понтон. - сила тяжести, действующая на понтон.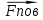 - поверхностная сила, действующая на понтон - поверхностная сила, действующая на понтонm — масса понтона 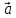 - ускорение понтона - ускорение понтонаТакже следует учесть, что 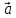 = = 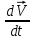 (6.3) (6.3)Поверхностную силу, действующую на понтон, можно разложить на две составляющие: 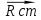 - гидростатическая сила (сила, действующая на понтон, находящийся в состоянии покоя), и - гидростатическая сила (сила, действующая на понтон, находящийся в состоянии покоя), и 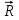 - гидродинамическая сила. - гидродинамическая сила.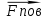 = = 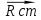 + + 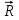 (6.4) (6.4)Но и гидродинамическую силу R, действующую на понтон, можно разложить на две составляющие: Rи - инерционная гидродинамическая сила, и Rо - гидродинамическая сила, действующая на понтон при его равномерном движении вертикально вверх. В проекции на ось Y уравнение будет иметь вид: -G +Rст +Rи -Rо = m*(dV/dt) (6.5) Запишем выражение для определения гидростатической силы: Rст = γ*V (6.6) где γ - удельный вес воды V- объем понтона Удельный вес воды определим по следующей формуле: γ = p*g (6.7) где р - плотность воды g - ускорение свободного падения тела Подставляя (6.7) в (6.6), получим Rcт = p * g * V (6.8) По условию, масса понтона составляет 5% массы воды в объеме, ограниченном наружной поверхностью понтона. Следовательно, m = 0.05*p*V (6.9) Тогда, если учесть, что G = m*g, то получим: G = 0.05 * p * V * g (6.10) Инерционная гидродинамическая сила равна: Rи = Rиу = 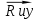 *L (6.11) *L (6.11)где 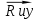 - удельная инерционная гидродинамическая сила, приходящаяся на единицу размаха, определяемая по формуле: - удельная инерционная гидродинамическая сила, приходящаяся на единицу размаха, определяемая по формуле: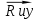 = - = - 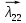 * *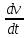 (6.12) (6.12)где 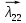 - присоединенная масса, приходящаяся на 1 погонный метр размаха понтона L - присоединенная масса, приходящаяся на 1 погонный метр размаха понтона L Присоединенную массу ( 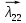 ) определим по следующей формуле ) определим по следующей формуле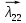 = = 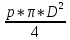 (6.13) (6.13)Подставляя (6.13) и (6.12) в (6.11), получим Rи = - 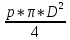 * L* * L*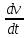 (6.14) (6.14)Понтон находится в безграничной идеальной жидкости, и гидродинамическая сила (Rо), действующая на понтон равна 0, согласно парадоксу Даламбера Rо = 0 (6.15) Перепишем уравнение движения цилиндра. Подставив (6.8), (6.9), (6.10), (6.14) и (6.15) в (6.5), получим 0.05 * р * V * g + p*g * V — р * V * (dv/dt) = 0.05 * р *V *(dv/dt) Поделив полученное выражение на произведение p* V, получим: -0.05 * g + g - (dv/dt) = 0.05 *(dv/dt) Преобразуем это выражение 0.95 * g = 1.05 * (dv/dt) Или dv = 8.87 * dt Решим полученное дифференциальное уравнение с разделяющимися переменными: 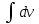 = 8,87* = 8,87*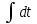 v = 8.87 * t + С Постоянную С определим из следующего условия: при t = 0; v = 0 => С = 0 Таким образом, получим: v(t) = 8.87*t (6.16) Выражение (6.16) представляет собой зависимость скорости всплытия понтона от времени Учитывая, что скорость - производная пути по времени, а понтон перемещается вдоль оси Y, получим: dy/dt = 8.87 * t Преобразуем это выражение: dy = 8.87 * t * dt Решим полученное дифференциальное уравнение с разделяющимися переменными: 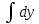 = 8,87* = 8,87*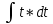 y= 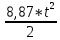 + С + СПостоянную С определим из следующего условия: при t = 0; у = 0 => С = О Таким образом, получим: y(t) = 4.435 * 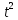 (6.17) (6.17) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
