Гидромеханика Курсовая работа. Гидромеханика. Курсовая работа Курсовая работа допущена к защите защищена с оценкой 202 г. Руководитель
 Скачать 4.6 Mb. Скачать 4.6 Mb.
|
|
4. Определение времени всплытия до момента соприкосновения понтона со свободной поверхностью Вычислим время всплытия понтона с момента отрыва его от дна до момента касания верхней точки понтона свободной поверхности. t = 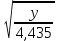 (6.18) (6.18)Мы приняли в начале задачи, что b = 22 м. - путь понтона от дна до свободной поверхности. Подставляя значение (b) вместо (у) в формулу (6.18), получим: t = 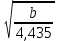 = 2.27 с. = 2.27 с.5. Определение скорости в момент соприкосновения понтона со свободной поверхностью Найдем скорость понтона в момент касания его верхней гранью свободной поверхности. v = 8.87*2.27 = 20.1 м/с Ответ: 1. Зависимость скорости от времени: v(t) = 8.87 * t 2. Время всплытия равно 2.27 с. 3. Скорость в момент всплытия равна 20.1 м/с. Задача №7 1. Содержание задачи Закреплённый на дне водоёма глубиной Н понтон освобождается от удерживающих его связей и всплывает. Найти зависимость скорости его всплытия от времени Vo(t), определить время всплытия до момента соприкосновения его со свободной поверхностью и скорость в этот момент, пренебрегая инерционной гидродинамической силой. 2. Исходные данные и принятые положения Длина понтона: L = 44 м. Диаметр понтона: D = 8 м. Глубина водоема: Н= 30 м. Плотность воды: р = 1025 кг/м^3 Ускорение свободного падения: g = 9,81 м/сек^2 В работе приняты следующие допущения: 1. Жидкость безгранична. 2. Жидкость считаем идеальной. 3. Понтон является частью цилиндра бесконечного размаха. 4. Инерционной гидродинамической силой пренебречь. В работе принята декартова система координат с началом отсчета в верхней точке понтона в момент его отрыва от грунта (причём с понтоном система координат не связана). При этом ось Z направлена вдоль оси понтона, ось X горизонтальна, а ось Y направлена вертикально вверх (см. рис. 7.1). 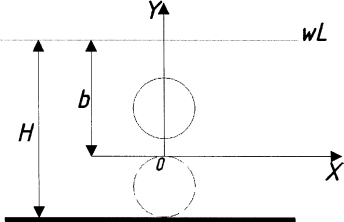 Рис 7.1 3. Составление уравнения движения понтона. Введем новую величину - b: расстояние от верхней точки понтона, лежащего на дне цилиндра, до свободной поверхности. b=H-D (7.1) где Н - глубина водоёма, D - диаметр понтона, b= 30 – 8 = 22 м. Таким образом, начало координат будет расположено на расстоянии 22 м. от свободной поверхности воды. Понтон всплывает вертикально вверх, так как силы, действующие на его боковые стороны, взаимно уравновешиваются в силу его симметрии. Следовательно, все силы, действующие на цилиндр во время его подъема, будут направлены вдоль оси Y. Составим уравнение движения цилиндра, учитывая, что положительное направление оси Y - вертикально вверх. 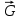 + + 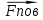 = m* = m* 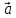 (7.2) (7.2)где 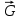 - сила тяжести, действующая на понтон. - сила тяжести, действующая на понтон.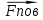 - поверхностная сила, действующая на понтон - поверхностная сила, действующая на понтонm — масса понтона 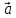 - ускорение понтона - ускорение понтонаТакже следует учесть, что 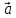 = = 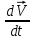 (7.3) (7.3)Поверхностную силу, действующую на понтон, можно разложить на две составляющие: 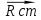 - гидростатическая сила (сила, действующая на понтон, находящийся в состоянии покоя), и - гидростатическая сила (сила, действующая на понтон, находящийся в состоянии покоя), и 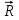 - гидродинамическая сила. - гидродинамическая сила.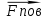 = = 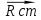 + + 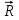 (7.4) (7.4)Но и гидродинамическую силу R, действующую на понтон, можно разложить на две составляющие: Rи - инерционная гидродинамическая сила, и Rо - гидродинамическая сила, действующая на понтон при его равномерном движении вертикально вверх. В проекции на ось Y уравнение будет иметь вид: -G +Rст +Rи -Rо = m*(dV/dt) (7.5) Запишем выражение для определения гидростатической силы: Rст = γ*V (7.6) где γ - удельный вес воды V- объем понтона Удельный вес воды определим по следующей формуле: γ = p*g (7.7) где р - плотность воды g - ускорение свободного падения тела Подставляя (7.7) в (7.6), получим Rcт = p * g * V (7.8) По условию, масса понтона составляет 5% массы воды в объеме, ограниченном наружной поверхностью понтона. Следовательно, m = 0.05*p*V (7.9) Тогда, если учесть, что G = m*g, то получим: G = 0.05 * p * V * g (7.10) Инерционная гидродинамическая сила равна нулю по условию: Rи = 0 (7.11) Понтон находится в безграничной идеальной жидкости, и гидродинамическая сила (Rо), действующая на понтон равна 0, согласно парадоксу Даламбера Rо = 0 (7.12) Перепишем уравнение движения цилиндра. Подставив (7.8) - (7.12) в (7.5), получим 0.05 * р * V * g + p*g * V = 0.05 * р *V *(dv/dt) Поделив полученное выражение на произведение p* V, получим: -0.05 * g + g = 0.05 *(dv/dt) Преобразуем это выражение 0.95 * g = 0.05 * (dv/dt) Или dv = 186.4 * dt Решим полученное дифференциальное уравнение с разделяющимися переменными: 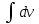 = 186.4 * = 186.4 *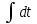 v = 186.4 * t + С Постоянную С определим из следующего условия: при t = 0; v = 0 => С = 0 Таким образом, получим: v(t) = 186.4 *t (7.13) Выражение (7.13) представляет собой зависимость скорости всплытия понтона от времени Учитывая, что скорость - производная пути по времени, а понтон перемещается вдоль оси Y, получим: dy/dt = 186.4 * t Преобразуем это выражение: dy = 186.4 * t * dt Решим полученное дифференциальное уравнение с разделяющимися переменными: 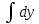 = 186.4 * = 186.4 *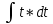 y=  + С + СПостоянную С определим из следующего условия: при t = 0; у = 0 => С = О Таким образом, получим: y(t) = 93,2 * 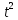 (7.14) (7.14)4. Определение времени всплытия до момента соприкосновения понтона со свободной поверхностью Вычислим время всплытия понтона с момента отрыва его от дна до момента касания верхней точки понтона свободной поверхности. t = 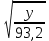 (6.18) (6.18)Мы приняли в начале задачи, что b = 22 м. - путь понтона от дна до свободной поверхности. Подставляя значение (b) вместо (у) в формулу (6.18), получим: t = 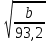 = 0.49 с. = 0.49 с.5. Определение скорости в момент соприкосновения понтона со свободной поверхностью Найдем скорость понтона в момент касания его верхней гранью свободной поверхности. v = 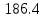 *0.49 = 91.5 м/с *0.49 = 91.5 м/сСравним результаты:
Вычислим ошибку в определении времени всплытия понтона и его скорости на финише, вызванную неучетом в расчете инерционной гидродинамической силы. t1/t2 = 2,27/0,49 = 4.6 v2/v1 = 91,5/20,1 = 4.6 Из-за неучёта инерционной гидродинамической силы время всплытия понтона уменьшилось в 4,6 раза, а скорость понтона на финише увеличилось в 4,6 раза. Список источников и литературы 1. Горянский Г.С. Гидромеханика: Учебно-методическое пособие по курсовой работе для студентов, обучающихся по направлению подготовки "Кораблестроение, океанотехника и системотехника объектов морской инфраструктуры" (профиль под-готовки "Кораблестроение"). - Калининград, ФГБОУ ВПО "КГТУ", 2015 г. - 26 с. 2. Ачкинадзе А.Ш. Гидромеханика: учебник / А.Ш. Ачкинадзе, А.Р. Бесядов-ский, В.В. Васильева, Н.В. Корнев, Ю.И. Фадеев. - СПб.: Морвест, 2007. - 552 с. 3. Овсянников М.К. Основы гидромеханики: учебник / Овсянников М.К., Орлова Е.Г. Емельянов П.С. – М.: РКонсульт, 2003 г. – 160 с. 4. Золотов С.С. Задачник по гидромеханике для судостроителей: учебн. посо-бие / С.С.Золотов, В.Б.Амфилохиев, Ю.И.Фаддеев. – Л.: Судостроение, 1984. – 232 с. 5. Бронштейн И.Н. Справочник по математике для инженеров и учащихся ВТУзов / И.Н, Бронштейн, К.А. Семендяев. - Москва: Наука, 1964. - 608 с. |
