Гидромеханика Курсовая работа. Гидромеханика. Курсовая работа Курсовая работа допущена к защите защищена с оценкой 202 г. Руководитель
 Скачать 4.6 Mb. Скачать 4.6 Mb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Факультет судостроения и энергетики Кафедра кораблестроения Курсовая работа Курсовая работа допущена к защите защищена с оценкой «___» ________202__г. Руководитель Руководитель ____________ __________ КУРСОВАЯ РАБОТА по дисциплине «Гидромеханика» КР.ГМХ.260302. ПЗ Нормоконтролёр Курсовую работу «_____» ____________2021 г. выполнил студент _________________________ «____» ________2021 г. Калининград, 2021 г. ОГЛАВЛЕНИЕ Стр. Общие положения 3 Задача №1 4 Задача №2 7 Задача №3 11 Задача №4 14 Задача №5 22 Задача №6 28 Задача №7 33 Список источников и литературы 38 Общие положения. Отчетная курсовая работа выполнена в соответствии с заданием, приведенным в приложении. Номер варианта задания - 20. В работе рассматривается цилиндрический понтон с плоскими, перпендикулярными его оси торцами, который плавает в морской воде с плотностью ρ=1,025 т/м3. Длина понтона L=44,0 м, диаметр понтона D = 8 м, глубина водоема H = 30,0 м, скорость понтона V0 = 12,0 м/с, интенсивность вихря на понтоне I = -0,9 м2/с. Понтон разделен поперечными водонепроницаемыми переборками на 3 равных по длине отсека. Масса пустого понтона m0 составляет 5% массы воды в объеме, ограниченном наружной поверхностью понтона. Объем конструкций понтона, включая обшивку, полагается пренебрежимо малым. Во всех случаях, кроме задачи № 1, дифферент понтона равен нулю. В задаче № 1 он определяется в ходе её решения. Состав входящих в работу задач и их решения приведены ниже. Задача №1 1. Содержание задачи. Понтон плавает таким образом, что один из его торцов полностью выступает из воды, а другой - касается её поверхности своей верхней кромкой (рис 1). Определить объемное водоизмещение понтона и силы избыточного гидростатического давления на погруженный торец Rт и на подводную часть цилиндрической поверхности Rц. При определении искомых величин принять, что понтон покоится на акватории без течений и ветра, т.е. решается гидростатическая задача. 2. Исходные данные и принятые положения: Длина понтона, L, м 44,0 Диаметр понтона, D, м 8 Положение понтона в воде см. рис. 1 Плотность воды, р, т/м^3 1,025 Ускорение свободного падения, g, м/сек^3 9,81 В работе принята декартова система координат с началом на свободной поверхности (см. рис 1). При этом оси X и Z лежат в продольно-вертикальной плоскости симметрии подводной части понтона (в диаметральной плоскости): ось X горизонтальна, а ось Z направлена вертикально. Ось Y перпендикулярна диаметральной плоскости (ДП). Ось симметрии понтона обозначена как ось 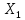 а перпендикуляр к ней в ДП - как ось а перпендикуляр к ней в ДП - как ось 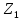 (см. рис 1). (см. рис 1).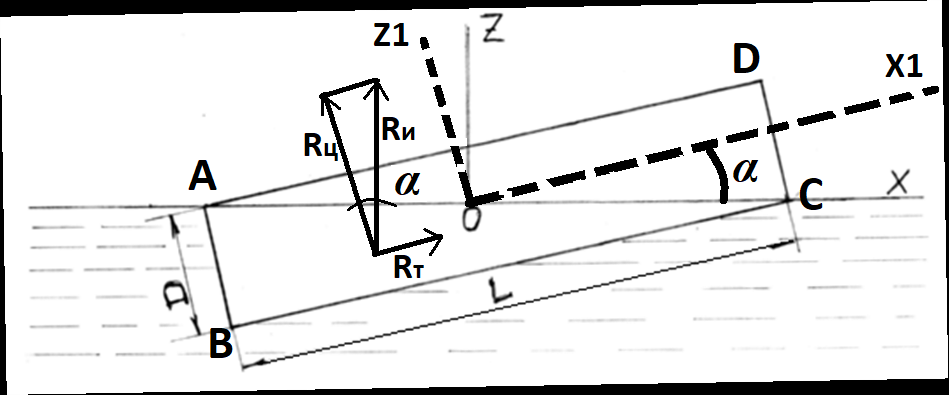 Рис.1 3. Определение объемного водоизмещения V. Объемное водоизмещение (объем подводной части) понтона V при описанной в п. 1 его посадке будет равно половине полного объема понтона Vn, т.е. V = 0,5*Vn = 0,5* 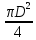 *L (1.1) *L (1.1)или V = 1105,28 м^3. (1.2) 4. Определение силы от избыточных давлений, действующей на всю смоченную поверхность понтона. В соответствии с п.1 задача решается в гидростатической постановке. В таком случае, как известно [1, п. 2.1] результирующая сила от избыточных давлений Rи, действующая на подводную часть тела (в нашем случае понтона), равна по модулю произведению удельного веса воды γ=10,055 Н/м^3 (при данных плотности и ускорении свободного падения) на объемное водоизмещение V: Rи= γ *V = 11113,5 Н, (1.3) направлена вертикально вверх по оси Oz (рис.1) и проходит через центр подводного объема понтона. Понтон в целом и его подводная часть, в частности, имеют продольно-вертикальную плоскость симметрии: диаметральную плоскость 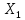 O O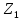 . .Следовательно, результирующая сила, от избыточных давлений Rилежит в диаметральной плоскости (ДП). 5. Определение сил избыточного давления, действующих на погруженный торец (сила Rт) и на подводную часть цилиндрической поверхности понтона (сила Rц). Ввиду симметрии понтона силы Rти Rц будут, как и результирующая сила Rи, лежать в диаметральной плоскости. При этом сила Rтбудет параллельна оси понтона Ох1 а сила Rц - перпендикулярна этой оси. Эти силы можно представить как катеты треугольника с гипотенузой, равной результирующей силе Rи. Так как один из катетов - сила Rцперпендикулярна оси понтона (оси Ох1), а гипотенуза - сила Rиперпендикулярна свободной поверхности водоема, (изображенной на рис. 1 как ось Ох), угол «α» между этими силами равен углу наклона оси понтона к поверхности воды, т.е. равен а = arctg (D/L) = 10.3°, (1.4) где D - диаметр понтона, a L - его длина. В соответствии с рис. 1 силы-катеты Rти Rцмогут быть выражены через известную гипотенузу Rи и найденный угол «α» по формулам: Rт = Rи * sin а = 2000,43 Н (1.5) и Rц = Rи * cos а = 10891,23 кН. (1.6) Ответы: V = 1105,28 м^3 Rт = 2000,43 Н, Rц = 10891,23 Н. Задача № 2. 1. Содержание задачи. Осадка понтона равна D/2. Найти силу избыточного гидростатического давления, действующую на участок наружной обшивки отсека понтона, ограниченный по его поперечному сечению центральными углами, равными 30° и 60°, отсчитывая их по часовой стрелке от ватерлинии (рис. 2).  Рис.2 2. Исходные данные и принятые положения. Длина понтона, L, м 44 Диаметр понтона, D, м 8 Радиус понтона, R=D/2, м 4 Положение понтона в воде см. рис.2 Плотность воды, р, т/м^3 1,025 Ускорение свободного падения, g, м/сек^2 9,81 Угол к поверхности от точки А, α, ° 30 Угол к поверхности от точки В, β, ° 60 В задаче принята декартова система координат со следующими осями: ось X направлена горизонтально (по поверхности жидкости), ось h направлена вертикально вниз, а ось Y направлена перпендикулярно плоскости чертежа («на нас»). 3. Решение. Силу избыточного гидростатического давления, действующую на участок наружной обшивки отсека понтона S, можно выразить через следующую формулу: Rи = 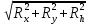 (2.1) (2.1)где Rx, Ry, Rh - проекции вектора Rи на соответствующие координатные оси. Эти проекции можно выразить в следующем виде: Rx= - γ * Sx* hcx Ry = - γ *Sy* hcy (2.2) Rh = - γ *Vтд где Sx и Sy - площади проекций поверхности понтона S на плоскости перпендикулярные координатным осям оХ и oY соответственно; γ = p * g - удельный вес воды; hcx и hcy — заглубления центров тяжестей Sx и Sy соответственно; Vтд - объем тела давления; Так как рассматриваемая поверхность перпендикулярна плоскости xOh, очевидно проекция поверхности на эту плоскость = 0, то есть Sy=0, а, следовательно, и Ry = 0. 3.1 Определение значения проекции вектора Rи на ось X(Rx): Определим значение Sx (см. рис. 2): Sx = CE*L/3=(OE-OC)*L/3 (2.3) По рисунку определяем, что: ОЕ = OB * cos(90 - β) (2.4) ОС = ОА* cos(90 - α) Учитывая, что OB=OA=R, и подставляя (2.4) в (2.3) получим: Sx = R * (cos(90 - β) — cos(90 - α))*L/3 (2.5) Подставляя необходимые исходные данные в (2.5), получаем: Sх = 21,47 м^2 Определим значение hcx: Hcx =OJ=CE/2+OC= (R*(cos(90 - β) - cos(90 - α)))/2+R* cos(90 - α) (2.6) Подставляя необходимые исходные данные в (2.6) получаем: hcx = 2,73 м Определим значение Rx: Rx= - γ * Sx* hcx = - р * g * Sx * hcx Rx = -589,4 kH 3.2 Определение значения проекции вектора Rи на ось h(Rh): Для того, чтобы найти значение Rh необходимо узнать величину объема тела давления (см. 2.2) Vтд = 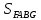 * *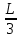 (2.7) (2.7)где L/3 - длина отсека. 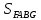 можно представить в следующем виде: можно представить в следующем виде: 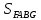 = = 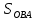 + + 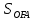 - - 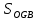 (2.8) (2.8)Фигура ОBА представляет собой сектор окружности. Следовательно, выражение для определения площади этой фигуры будет иметь вид: 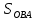 =π* =π*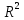 * * , где n - угол сектора. , где n - угол сектора.В нашем случае: 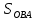 =π* =π*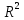 * *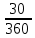 =( π* =( π*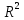 )/12 (2.9) )/12 (2.9)Фигура OFA является прямоугольным треугольником. Его площадь равна: 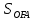 =1/2 * OF * FA (2.10) =1/2 * OF * FA (2.10)Из рисунка определяем: OF = ОА*cos α = R*cos α (2.11) FA = OA*sin α = R* sin α Подставляя (2.11) в (2.10), получаем: 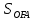 = ½* = ½* 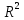 * cos α * sin α=( * cos α * sin α=(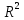 *sin α )/4 (2.12) *sin α )/4 (2.12)Фигура OGB также является прямоугольным треугольником. Его площадь равна: 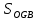 =1/2*OG*GB (2.13) =1/2*OG*GB (2.13)Из рисунка определяем: 0G = OB * cos β = R * cos β (2.14) GB = ОB * sin β = R * sin β Подставляя (2.13) в (2.14), получаем: 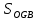 = ½* = ½* 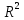 * cos β * sin β =( * cos β * sin β =(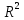 *sin2 β)/4 (2.15) *sin2 β)/4 (2.15)Поставим (2.9), (2.12), и (2.15) в (2.8) и получим: 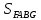 = ( π* = ( π*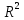 )/12 + ( )/12 + (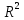 *sin2 α)/4 - ( *sin2 α)/4 - (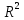 *sin2 β)/4 *sin2 β)/4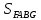 = 4,18 m^2 (2.16) = 4,18 m^2 (2.16)Подставляя (2.16) в (2.7), получим: Vтд = 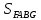 * *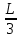 Vтд = 61.3 m^3 Определим значение Rh: Rh = - γ *Vтд = - р * g*Vтд Rh = -616,4 kH 3.3 Определение значения силы избыточного гидростатического давления Rи: Подставив найденные значения Rh и Rx в (2.1), и, учитывая, что Ry =0, получим: Rи = 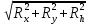 Rи = 852,8 кН Ответ: Rи = 852,8 кН Задача №3 1. Содержание задачи. Определить вертикальное усилие, необходимое для подъема понтона с илистого грунта, если все его отсеки затоплены забортной водой и с ней сообщаются, ось понтона находится на глубине, равной D, а днище соприкасается с грунтом на участке шириной а = D/4 (рис. 3). 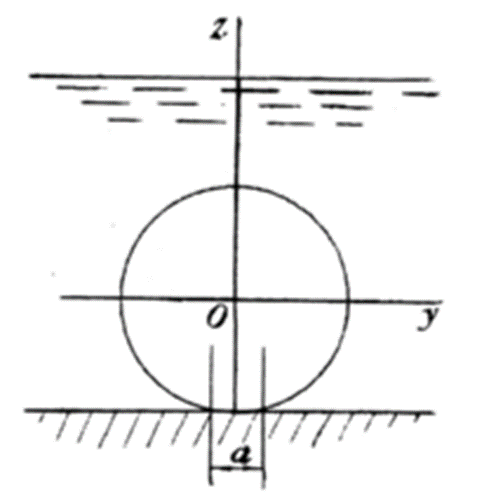 Рис. 3 2. Исходные данные и принятые положения. Длина понтона, L, м 44 Диаметр понтона, D, м 8 Глубина водоема, Н, м 30 Плотность воды, р, т/м 1,025 Ускорение свободного падения, g, м/сек 9,81 3. Решение. 3.1 Уравнение равновесия. При нахождении понтона на дне, его уравнение равновесия будет иметь вид: F - G + N - Rгид = 0 F- сила поднятия понтона, (искомая сила отрыва); Rгид - гидростатическая сила; N - сила реакции опоры; G - сила тяжести понтона; В момент отрыва понтона от дна сила реакции опоры N будет равна 0, а искомая сила F примет свое максимальное значение. В таком случае уравнение равновесия преобразуется и будет иметь следующий вид: F = Rгид + G (3.1) 3.2 Определение силы тяжести понтона G Для того, чтобы определить силу тяжести, действующую на понтон, воспользуемся следующей формулой: G = m* g (3.2) Масса понтона m составляет 5% массы воды в объеме, ограниченном наружной поверхностью понтона. m = М * 0.05 (3.3) где m - масса понтона; М - масса воды, заполнившей понтон; М = р* V (3.4) ,где р - плотность воды; V - объем понтона. Так как понтон имеет цилиндрическую форму, его объем равен: V = 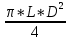 V = 2210,5 м^3 (3.5) Подставляя (3.5) в (3.4) получаем: М= 2265,8 т (3.6) Определим массу понтона, подставив (3.6) в (3.3) m = М*0.05 = 113,3 т (3.7) Подставив (3.7) в (3.2), определим силу тяжести G G=m*g=1111,4 кН (3.8) 3.3 Определение гидростатической силы Rгид Если пренебречь толщиной стенок понтона, то можно считать, что площадь внутренней поверхности равна площади внешней поверхности понтона. Понтон полностью затоплен водой и происходит обмен с забортной водой, значит, на все участки обшивки понтона, кроме тех, которые соприкасаются с дном, действуют равные давления воды с внешней и внутренней сторон. Следовательно, и результирующие гидростатические силы от этих давлений равны нулю на все поверхности понтона, кроме площадки касания с грунтом. На этом участке с внутренней стороны будет действовать гидростатическая сила: Rгид =pa*S (3.9) где ра - абсолютное давление на участок понтона, погруженный в грунт; S - площадь участка понтона, погруженного в грунт. Воспользуемся основным законом гидростатики и получим: pа = pо + γ*Н (3.10) где ро - атмосферное давление (101,3 кПа при н.у.) γ - удельный вес жидкости; Н — глубина затопления поверхности. Тогда гидростатическая сила, действующая на участок понтона, погруженный в грунт, определяется следующим образом: Rгид = pа * S = (pо + γ H) * S = (рo + р * g * Н) * D/4 * L Rгид = 3,54 * 10^4 кН (3.11) 3.4 Определение силы поднятия понтона (F) Подставляя (3.8) и (3.11) в (3.1) определим искомую силу: F = G + Rгид F =36571,6 кН Ответ: F = 3,65 * 10^4 кН Задача №4 1. Содержание задачи. Рассматривая понтон как цилиндр, находящийся в безграничной идеальной жидкости (рис.4.1), однородный поток, который набегает на него перпендикулярно оси симметрии понтона со скоростью Vо, построить картину линий тока течения для поперечного сечения цилиндра, пренебрегая влиянием конечности его размаха. Найти также распределение гидродинамического давления по цилиндру и построить эпюру скоростей в точках оси OY. При построении линий тока течения промежутки между соседними линиями тока следует выбирать из условия: 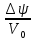 = =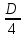 , ,где  - разность значений функции тока - разность значений функции тока 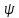 на соседних линиях тока. на соседних линиях тока.Ориентировочные размеры картины линий тока: ±2D относительно оси OY и ±1,5D относительно оси ОХ. Плотность жидкости следует принять равной плотности воды. 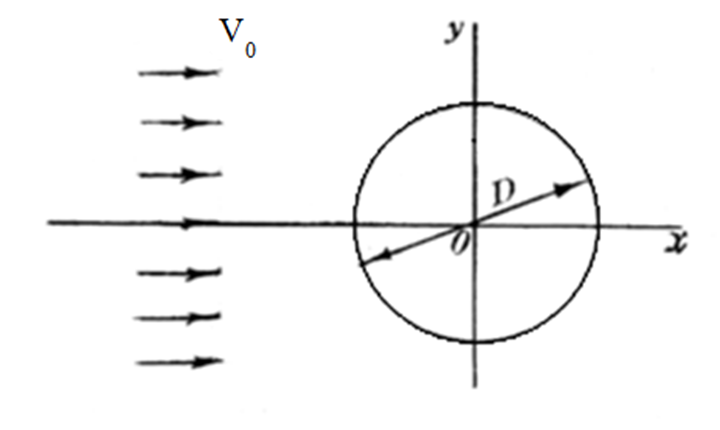 Рис. 4.1 |
