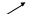Производная функция и ее применение. Методика изучения темы «Производная функция и ее применение» в а. Курсовая работа Методика обучения учащихся исследованию функций с помощью производной

• Название: Курсовая работа Методика обучения учащихся исследованию функций с помощью производной
• Анкор: Производная функция и ее применение
• Дата: 22.06.2021
• Размер: 0.74 Mb.
• Имя файла: Методика изучения темы «Производная функция и ее применение» в а.doc
• Тип: Курсовая; #220201
• страница: 2 из 3

§2. Применение общей схемы к исследованию функций

Теоретический материал, который требуется для изучения исследований функций с помощью производной уже известен учащимся. В данной теме фактически систематизируются знания учащихся, относящиеся к вопросам нахождения промежутков возрастания (убывания) и экстремумов, показывается общий метод получения результатов. Таким образом, изучение этой темы завершает рассмотрение теоретических вопросов, связанных с исследованием функций. Все положения, которые нужно отразить в решении задания на исследование, имеют теоретические обоснования, общие методы решения.

В ходе изучения этой темы учащиеся должны научиться проводить исследование функций по общей схеме и строить их графики. Построения графика функции необходимо начинать с исследования функции, которое состоит в том, что для данной функции:

1. 
   находят ее область определения;
   
2. 
   выясняют, является ли функция четной или нечетной, является ли периодической;
   
3. 
   точки пересечения графика с осями координат;
   
4. 
   промежутки знакопостоянства;
   
5. 
   промежутки возрастания и убывания;
   
6. 
   точки экстремума и значения в этих точках;
   
7. 
   исследуют поведение функции в окрестности «особых» точек и при больших по модулю ;
   

На основании такого исследования строится график функции.

Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции и ее критические точки, а затем выясняют, какие из них являются точками экстремума.

Пример 1. Исследуем функцию и построим ее график.

Проведем исследование по указанной схеме.

1) , так как - многочлен.

2) Функция не является ни четной, ни нечетной

3) График пересекается с осью ординат в точке чтобы найти точки пересечения с осью абсцисс, надо решить уравнение , один из корней легко найти . Другие корни (если они есть) могут быть найдены только приближенно. Промежутки знакопостоянства не находим.

4) Найдем производную функции :



, поэтому критических точек, для которых не существует, нет.

Заметим, что , если , т.е. при значениях аргумента, равных 0,-1 и 1. Рассматриваемая функция имеет три критические точки.

Составляем таблицу:

	+		−		−		+
		max				min

В первой строке этой таблицы указаны в порядке возрастания критические точки функции и ограниченные ими промежутки. В третьей строке записаны выводы о ходе изменения данной функции. Критическая точка равная 0 функции не является точкой экстремума [2].

Строим график функции (рис.1). Строить его удобно по промежуткам, которые указаны в таблице.

Пример 2. Исследовать функцию

1)

2) Функция четная, исследование ее можно проводить на промежутке .

3) Найдем точки пересечения графика функции с осями координат, т.е. решим уравнение . Пусть тогда уравнение примет вид: или , т.е. или , не имеет решения. Получили две точки пересечения с осью абсцисс . График пересекает ось ординат в точке .

4) Найдем производную функции

5) Найдем критические точки функции:

а) , если , , или , или

б) определена на всей

6) Определим знак производной на промежутках, найдем значения в точках -1, 0, 1. Полученные данные занесем в таблицу и построим график [2].

	−		+		−		+
		Min		max		min

Построим график данной функции (рис. 2):

Приведем примеры заданий для самостоятельной работы по исследованию функций.

Исследуйте функцию и постройте ее график:

1)

2)

3)

4)

5)

После изучения данной темы учащимся предлагается контрольная работа.

Контрольная работа по теме «Производная и ее применение»

I вариант

1. Дана функция . Найдите:

а) промежутки возрастания и убывания функции;

б) точки экстремума;

в) наибольшее и наименьшее значения функции на отрезке .

2. Постройте график функции .

3. Составьте уравнение касательной к графику функции в точке с абсциссой .

4. В какой точке касательная к графику функции параллельна прямой ?

5. Найдите наибольшее и наименьшее значения функции на отрезке .

II вариант

1. Дана функция . Найдите:

а) промежутки возрастания и убывания функции;

б) точки экстремума;

в) наибольшее и наименьшее значения функции на отрезке .

2. Постройте график функции .

3. Составьте уравнение касательной к графику функции в точке с абсциссой .

4. В какой точке касательная к графику функции параллельна прямой ?

5. Найдите наибольшее и наименьшее значения функции на отрезке [10].

§3. Типичные ошибки учащихся при исследовании функций

При проведении исследования функций учащиеся часто допускают ошибки. Большое число ошибок допускается при построении графиков функции с использованием производной.

а) Пусть требуется исследовать с помощью производной функцию и построить ее график. Результаты исследования функции оформим в виде таблицы (таб. 1).

Таблица 1

				0
	+	0	−	0	+		−
				0
		Max		min		max

Покажем ошибочные эскизы графиков, которые учащиеся изображают по данной таблице (рис. 3,4,5,6)



Рис.4


Рис.3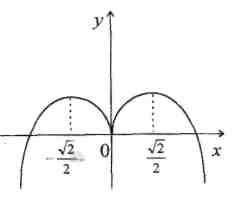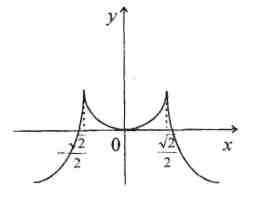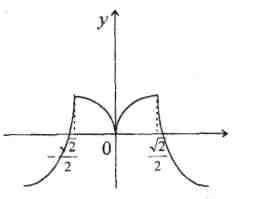





Рис.5

Рис.6


На каждом из этих рисунков допущены грубые математические ошибки и происходят они из-за того, что учащиеся используют из таблицы лишь сведения о том, где функция возрастает и где убывает, и совершенно не берут во внимание существование производной функции в критических точках. В таблице 1 отмечено, что в точках, производная функции существует, а это означает, что в точках с этими абсциссами можно провести касательную. Тот факт, что производная функции в этих точках равна нулю, означает, что в точках с этими абсциссами касательные к кривой должны быть параллельны оси Ox. Анализ рисунков 3,4,5,6 показывает, что указанное выше требование нарушено, а именно, на рисунке 3 нельзя провести касательную к кривой с абсциссой ; на рисунках 4 и 5 – в точках с абсциссами ; на рисунке 6 – в точках с абсциссами .

Правильный график функции 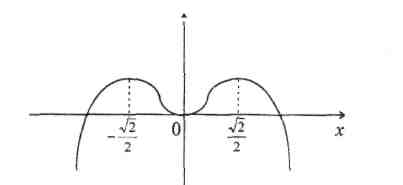показан на рисунке 7.



Рис.7



б) При исследовании функции на монотонность учащиеся очень часто не учитывают точек, в которых функция неопределенна. Приведем пример такой ошибки.

Исследовать функцию на монотонность.

Часто учащиеся поступают так: ; находят точки, в которых производная равна нулю: ; затем, множество всех действительных чисел разбивают точкой на два промежутка находят знаки производной на каждом промежутке и делают затем ошибочный вывод о монотонности функции на каждом из этих двух промежутков.

Поступать же надо было так. Множество всех действительных чисел следовало бы разбить на промежутки точками, в которых функция не определена и точками в которых производная равна либо нулю, либо равна бесконечности, либо не существует. В данном случае мы получим три промежутка: . Знак производной функции на каждом из них отмечен на рисунке 8.



Рис.8



Ответ должен быть записан в следующем виде:

на промежутке функция возрастает;

на промежутке функция убывает;

на промежутке функция возрастает.

По поводу записи ответа отметим следующее: если функция непрерывна в каком-либо из концов промежутка возрастания (убывания), то его можно присоединить к этому промежутку. Так, в нашем случае, в точке функция непрерывна, а значит промежутки могли бы быть записаны так: .

в) Ряд ошибок связан с решением текстовых задач на экстремум. Проанализируем эти ошибки.

Очень часто учащиеся в процессе решения задач на экстремум при исследовании полученной функции на наибольшее (наименьшее) значение делают такой вывод: «Функция на промежутке имеет один максимум, тогда максимальное значение и будет наибольшим». Такое утверждение содержит ошибки, разберем суть этих ошибок.

Н
а рисунке 9 показан график такой функции, которая на промежутке имеет одну точку максимума, но максимальное значение не является

наибольшим; наибольшее значение функция достигает в точке .

У
Рис.9
чащиеся были бы почти правы, если бы они записали вывод в таком виде: «Функция на промежутке имеет один экстремум, который максимум, тогда максимальное значение будет и наибольшим на данном промежутке». Этому утверждению соответствует рисунок 10.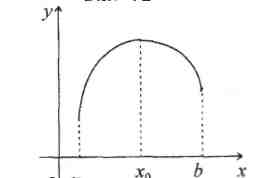




Рис.10


Но и последнее утверждение содержит ошибку. На рисунке 9 показан график функции, которая на отрезке 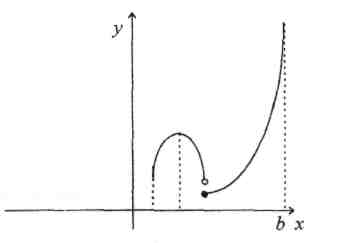имеет одну точку экстремума, которая является точкой максимума, но максимальное значение не является на этом промежутке наибольшим; наибольшее значение достигается при .



Рис.11



Обобщая проведенные рассуждения, вывод, сделанный учащимися, должен быть таким: «Непрерывная функция имеет на промежутке одну точку экстремума, которая является точкой максимума, тогда это максимальное значение и будет наибольшим на указанном промежутке».

Приведенных в работе примеров типичных ошибок, допускаемых учащимися при изучении Алгебры и начал анализа, вполне достаточно, чтобы показать учителю насколько важно учить учеников, а им самим учиться, рефлексивно- оценочной деятельности, которая позволит устранить и предупредить подобного рода ошибки [5].