Применение производной к исследованию функций на монотонность и экстремумы
 Скачать 469.24 Kb.
|
|
МКОУ «Дибгашинская СОШ им. С. Рабаданова» План- конспект открытого урока по алгебре в 10 кл. Тема «Применение производной к исследованию функций на монотонность и экстремумы» Провела учительница математики - Маммаева Аминат Алиевна. 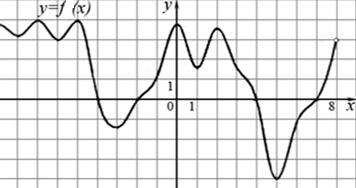 Дата проведения Тема «Применение производной к исследованию функций на монотонность и экстремумы» Тип урока: урок формирования новых знаний, обретения новых умений и навыков Дидактическая цель: создать условия для активизации познавательной деятельности с помощью технологии проблемного обучения и активизации обучения. Цели по содержанию: Образовательная: формирование навыков прикладного использования аппарата производной; выявление уровня овладения учащимися комплексом знаний и умений по исследованию функции; Дать представление о связи свойств функции с её производной, учить чтению и анализу графиков функций. Развивающая: Развитие способности к самостоятельному планированию и организации работы; навыков применение информационных технологий; умений обобщать и конкретизировать знания при исследовании функции; навыков частично-поисковой деятельности Воспитательная: Воспитание познавательного интереса к математике; самостоятельности, способности к коллективной работе; информационной культуры и культуры общения. Необходимое оборудование и материалы: Доска, мультимедийная разработка урока, бланки листов для проведения контроля, звуковое сопровождение, проектор, презентация. Методы обучения: частично-поисковый. Формы организации работы: фронтальная, групповая, коллективная Структура урока: Мотивационно-ориентировочная часть Изучение нового материала. Рефлексивно-оценочная часть Ход урока Оргмомент - Ребята, здравствуйте, садитесь! - Сегодня у нас необычный урок, к нам приехали гости, посмотрите на них и улыбнитесь. Посмотрите друг на друга и тоже улыбнитесь, ведь веселому человеку легче добиться успеха. А успех нам необходим. Я бы хотела познакомить вас с тем, что нам предстоит сегодня выполнить: Проверка домашнего задания Устная работа Обсуждение проблемной ситуации. Изучение нового материала (исследовательская работа) Закрепление Итог урока Домашнее задание. Откроем тетради, запишем число и тему сегодняшнего урока. Тема урока «Применение производной для исследования функций на монотонность и экстремумы» Для чего нужно исследование функций? (Для построения графиков). Это мы умели и раньше до изучения темы производная. При исследовании функций и построении их графиков широко используются производные, т. к. это облегчает этот процесс. Выдающийся русский математик и кораблестроитель академик Алексей Николаевич Крылов (1863-1945г.) однажды заметил, человек обращается к математике « не затем, чтобы любоваться неисчислимыми сокровищами, ему, прежде всего, нужно ознакомиться со столетиями испытанными инструментами и научиться ими правильно и искусно владеть». С одним из таких инструментов мы уже знакомы – это производная. Мы сегодня сформируем начальное представление о приложениях производной в математике и в жизни, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями её производной; и рассмотрим применение производной для решения задач В8, В14 из материалов ЕГЭ. Актуализация опорных знаний учащихся Проверка домашнего задания(Выяснить есть у учащихся вопросы ) Блиц-опрос теоретический Учащиеся поднимают руку, если согласны с утверждением, и не поднимают – если не согласны. В точке возрастания функции её производная больше нуля. (Верно). Если производная функции в некоторой точке равна нулю, то это критическая точка. Производная произведения равна произведению производных. (Неверно). Наибольшее и наименьшее значения функции на некотором отрезке наблюдаются или в стационарных точках, или на концах отрезка. (Верно). Любая точка экстремума является критической точкой. (Верно). 3 Задания классу: (на интерактивной доске.) А)Составьте уравнение касательной к графику функции 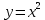 в точке с абсциссой х=1. Какие у вас получились уравнения касательных?()а) у =6х-9 б) у = - х + 2 в) у = 2х – 1 г) у = - 5х - 1 (Ответ в)) Б) Классу. Материальная точка движется прямолинейно по закону x(t)=3t2+2t+27, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=2c. (14м/с) Карточки(В то время как уч класса выполняют задание трём ученикам ) Укажите количество промежутков монотонности функции (10)На графике функции найдите промежутки убывания и в ответе укажите сумму длин этих промежутков (12)  На графике найдите промежутки возрастания и в ответе укажите сумму длин этих промежутков (11) 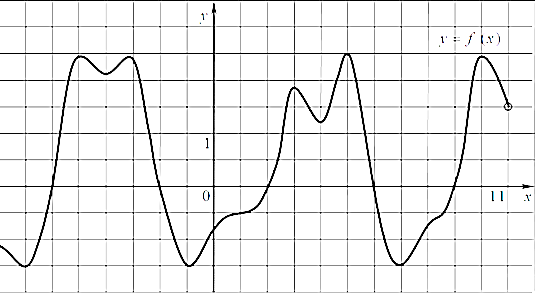 Изучение нового материала. а) Постановка проблемы
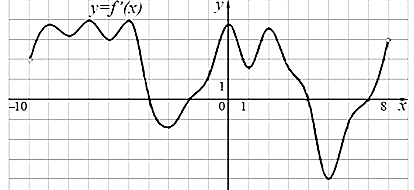
(По результатам работы на данном этапе урока учащиеся констатируют: задание для них является невыполнимым). б) Включение в деятельность - Перед нами возникает проблема (задача). Мы не можем ответить на данные вопросы. -Что же делать, как нам выполнить это задание? (нам нужно разработать правило, с помощью которого мы сможем указать промежутки возрастания и убывания, а также узнать, что такое точки экстремума и как их определять, используя график производной функции). в) Предварительная работа (Слайд) (Изучим следующие утверждения) 1) Если функция f(x) во всех точках открытого промежутка Х имеет положительную производную т.е. выполняется неравенство f’(x)≥0, то функция y = f(x) возрастает на промежутке Х. 2) Если во всех точках открытого промежутка Х выполняется неравенство f’(x)≤0, то функция y = f(x) убывает на промежутке Х. - Рассмотрим пример: 1. Найдите интервалы возрастания и убывания функции: f(x)=  .Данная функция определена и имеет производную на всей числовой прямой. Так какf ‘ (x)=  то f’(x)>0 (решая методом интервалов неравенства, получим) на интервалах (-∞;1) и (2;+∞) и f’(x)<0 на интервале (1;2).Ответ: (-∞;1) и (2;+∞) интервалы возрастания, (1;2) интервал убывания. Вывод: Промежутки, на которых функция возрастает или убывает, называются её промежутками монотонности. И обратно: В любой точке х из области определения убывающей дифференцируемой функции:f ’ (x) ≤ 0. Первичное закрепление 2.Для закрепления по вариантам: Выберите верные утверждения: Вариант 1 (слайд)После исследования на монотонность функции  получилось, что:Выберите: 1) функция возрастает на промежутке  2) функция убывает на промежутке 3) функция убывает на промежутке  4) функция возрастает на промежутке Верные ответы: 1; 3; Вариант2 Выберите верные утверждения: После исследования на монотонность функции  получилось, что:Выберите несколько из 6 вариантов ответа: 1) функция убывает на промежутке  2) функция возрастает на промежутке 3) функция возрастает на промежутке  Верные ответы: 2; 4; 5; 4) функция возрастает на промежутке  5) функция убывает на промежутке 6) функция убывает на промежутке 3. Классу(слайд)  + +++    + Красной отмечаны промежутки, в которых f’(x)>0, а остальные? Сколько промежутков возрастания у этой функции? Найдите длину большего промежутка убывания этой функции. 4.Точки в которых производная равна нуль или не существует, называются критическими точками этой функции. Назовите по заданному рисунку точки(абсциссы) у которых производная равна нулю. И ещё в этих точках касательная параллельна оси абсцисс. Дать определение точек максимума и минимума. №1(Задание №7 ЕГЭ проф. математика) По графику функции y=f ´(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько промежутков возрастания у этой функции? Найдите длину промежутка убывания этой функции.   №2Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции №3 Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество точек графика этой функции, в которых касательная параллельна оси ОХ.  Закрепить правило (алгоритм), с помощью которого можно исследовать функции на монотонность и экстремумы по её производной. Для этого решить №296(а; б), №299(а; б)В ходе обсуждения выводов учащихся, необходимо отметить, что для того, чтобы исследовать функцию на монотонность и экстремумы, необязательно строить график производной, достаточно определить знаки производной на промежутках, на которые стационарные и критические точки разбивают область определения функции. Фактически составляется алгоритм исследования непрерывной функции на монотонность и экстремумы:
Рефлексивно-оценочная часть Итог урока: Сегодня мы закрепили умения исследовать функции с помощью производных и строить их графики; «читать» графики функций. Данные умения и знания пригодятся вам в жизни и в вашей профессиональной деятельности. Отмечаются позитивные моменты урока, и, обязательно, надо отметить то, что каждый ученик на уроке занимался исследовательской деятельностью, создавая свой интеллектуальный продукт. Домашнее задание §24, пункт 1, 2, выучить формулировки теорем и алгоритм исследование функции на монотонность и экстремумы, №296(в; г), 297(в; г), 299(в; г) Спасибо за урок! |
