Курсовая работа Объем многогранников. Объем многогранников .. Курсовая работа Научный руководитель доцент, к п. н. Кузина Наталья Георгиевна Ульяновск, 2014 Содержание
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ульяновский государственный педагогический университет имени И. Н. Ульянова» Кафедра методики преподавания математики и информатики Выполнила студентка 2 курса физико-математического факультета группы МИ-12 Кирькина Анна Александровна Объем многогранников Курсовая работа Научный руководитель доцент, к.п.н. Кузина Наталья Георгиевна Ульяновск, 2014 Содержание Введение……………………………………………………………………………3 Глава 1. Многогранники и круглые тела…………………………………………6 §1. Историческая справка……………………………………………………6 §2. Понятие многогранника. Виды многогранников………………………8 §3. Свойства многогранников и круглых тел……………………………...13 §4. Теорема Эйлера………………………………………………………….13 Глава 2. Объемы многогранников и круглых тел……………………………….14 §1. Объем геометрических фигур…………………………………………..14 §2. Различные подходы к определению объема многогранников………..17 §3. Объем многогранника в евклидовом пространстве…………………...19 §4. Принцип Кавальери……………………………………………………...21 Глава 3. Тематические задачи…………………………………………………….23 §1. Объем цилиндра…………………………………………………………23 §2. Объем призмы…………………………………………………………..25 §3. Объем параллелепипеда…………………………………………………26 §4. Объем пирамиды………………………………………………………...27 §5. Объем шара………………………………………………………………28 Заключение………………………………………………………………………..30 Литература…………………………………………………………………………31 Введение. Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности - от двухлетнего ребёнка, играющего деревянными кубиками, до зрелого математика. Особый интерес к многоугольникам и многогранникам связан с красотой и совершенством формы. Они довольно часто встречаются в природе. Достаточно вспомнить форму снежинок, граней кристаллов, ячеек в пчелиных сотах. Эта тема выбрана потому, что понятие многогранника является одним из центральных в курсе стереометрии. Многогранники интересны и сами по себе. Они имеют красивые формы. Формы многогранников находят широкое применение в конструировании сложных и красивых многогранных поверхностей, которые используются в реальных архитектурных проектах. Идёт это с глубокой древности. Пирамида - это норма тектоники - внутреннего устройства каменных зданий прошлого. (В частности пирамида Хеопса, имеют форму многогранников). Силуэты каменных церквей и соборов, как правило, вписываются в форму пирамиды. «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не случайно говорят, что пирамида Хеопса - немой трактат по геометрии, а греческая архитектура - внешнее выражение геометрии Евклида. «Прошли века, но роль геометрии не изменилась. Она по-прежнему остаётся грамматикой архитектора» - это высказывание принадлежит великому французскому архитектору Ле Корбюзье. (1887-1965). Поэтому захотелось больше узнать о многогранниках. Для продуктивной деятельности в современном информационном мире требуется достаточно прочная базовая математическая подготовка, поэтому изучение темы «Объемы многогранников» очень актуально, так как они необходимы для изучения смежных дисциплин, для продолжения образования. Тема «Объемы » - одна из центральных тем в курсе стереометрии средней школы. Проблема организации уроков по изучению объемов многогранников одна из самых актуальных, так как она занимает значительную часть в курсе стереометрии. Во всяком подлинно геометрическом предложении, будь то аксиома, теорема или определение, неразрывно присутствуют эти два элемента: наглядная картина и строгая формулировка, строгий логический вывод. Там, где нет ни одной из двух сторон, нет и подлинной геометрии. Именно при изучении многогранников и их объемов решение данной задачи выступает наиболее ярко, и их рассмотрению должно быть уделено больше внимания, потому что многогранники дают особенно богатый материал для развития пространственных представлений, для развития того соединения живого пространственного воображения со строгой логикой, которая составляет сущность геометрии. Объект исследования - процесс обучения стереометрии в средней школе. Предмет исследования - изучение объемов многогранников в курсе стереометрии. Основная цель исследования - разработать методические рекомендации по изучению темы «Объемы многогранников» в курсе стереометрии. Гипотеза исследования : Если на уроках геометрии использовать такие формы подачи нового материала, как лабораторные работы, решение на уроках задач, направленных на развитие различных процессов мышления, привлечение учащихся к факультативным занятиям, использование на уроках наглядных пособий и моделирование фигур, то формирование пространственных представлений учащихся 7-9 классов будет проходить более эффективно. Для достижения поставленной цели необходимо решить следующие задачи: изучить психологическую, педагогическую и методическую литературу по данной проблеме; выявить и описать условия развития пространственного представления учащихся 7-9 классов; определить наиболее эффективные методы и средства для формирования и развития пространственных представлений, а также виды учебных задач, используемые в практике учителей для развития пространственных представлений; предложить модели уроков, программу факультатива и лабораторных работ на которых при изучении теории и решении практических задач основной упор ставится на визуальное восприятие учеником материала; разработать методические рекомендации и систему упражнений, способствующую развитию пространственных представлений у школьников. Глава 1. Многогранники и круглые тела. §1. Историческая справка. Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал ее богатства. В процессе практической деятельности он накапливал геометрические сведения. Материальные потребности побуждали людей изготовлять орудия труда, обтесывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Конечно, десятки и сотни тысяч раз натягивали люди свои луки, изготовляли разные предметы с прямыми ребрами и т. п., пока постепенно дошли до отвлеченного понятия прямой линии. Примерно то же можно сказать о других основных геометрических понятиях. Практическая деятельность человека служила основой длительного процесса выработки отвлеченных понятий, открытия простейших геометрических зависимостей и соотношений. Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI – V вв. до н. э. в Древней Греции в геометрии начался новый этап развития, что объясняется высоким уровнем, которого достигла общественно-политическая и культурная жизнь в греческих государствах. Произведения, содержащие систематическое изложение геометрии, появились в Греции еще в V до н. э., но они были вытеснены “Началами” Евклида. Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в “Началах” Евклида. Конечно, изложенная в “Началах” наука геометрия не могла быть создана одним ученым. Известно, что Евклид в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др. Ценой больших усилий, исходя из отдельных геометрических сведений, накопленных тысячелетиями в практической деятельности людей, эти великие ученые сумели на протяжении 3 – 4 столетий привести геометрическую науку к высокой ступени совершенства. Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени. На протяжении двух тысячелетий геометрия изучалась в том объеме, порядке и стиле, как она была изложена в “Началах” Евклида. Многие учебники элементарной геометрии во всем мире представляли (а многие и поныне представляют) собой лишь переработку книги Евклида. “Начала” на протяжении веков были настольной книгой величайших ученых. В XVII в. Декарт, благодаря методу координат, сделал возможным изучение свойств геометрических фигур с помощью алгебры. С этого времени начала развиваться аналитическая геометрия. В XVII – XVIII вв. зарождается и разрабатывается дифференциальная геометрия, изучающая свойства фигур с помощью методов математического анализа. В XVIII – XIX вв. развитие военного дела и архитектуры привело к разработке методов точного изображения пространственных фигур на плоском чертеже, в связи с чем появляются начертательная геометрия, научные основы которой заложил французский математик Г. Монж, и проективная геометрия, основы которой были созданы в трудах французских математиков Д. Дезарга и Б. Паскаля (XVII в.). В ее создании важнейшую роль сыграл другой французский математик — Ж.-В. Понселе (XIX в.). Коренной перелом в геометрии впервые произвел в первой половине ХIХ в. великий русский математик Николай Иванович Лобачевский, который создал новую, неевклидову геометрию, называемую ныне геометрией Лобачевского. Открытие Лобачевского было началом нового периода в развитии геометрии. За ним последовали новые открытия немецкого математика Б. Римана и др. В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники. §2. Понятие многогранника. Виды многогранников. Многогранником называется геометрическое тело, поверхность которого состоит из частей плоскостей, ограниченных многоугольниками. Гранями многогранника называются части плоскостей, ограничивающие многогранник. Для краткости говорят, что гранями многогранника служат многоугольники, которые ограничивают многогранник. Ребрами многогранника называются общие стороны смежных многоугольников. Вершинами многогранника называются вершины многогранных углов, образованных его гранями, сходящимися в одной точке. Диагональю многогранника называется отрезок прямой, проходящей через две вершины многогранника, не лежащие на одной грани. Будем рассматривать только выпуклые многогранники, т. е. такие, все грани которых лежат по одну сторону от каждой из его граней, неограниченно продолженной. Призма. Призмой называется многогранник, две грани которого параллельны, а остальные грани пересекаются по параллельным прямым. Построение призмы. Возьмем какой-нибудь многоугольник ABCDE и через его вершины проведем прямые, параллельные между собой, не лежащие в плоскости этого многоугольника. На одной из параллельных прямых возьмем произвольную точку М и проведем через нее плоскость, параллельную плоскости многоугольника ABCDE. Затем через каждые две параллельные прямые, исходящие из двух соседних вершин многоугольника, проведем плоскости. Полученное геометрическое тело, ограниченное всеми построенными плоскостями, и будет призмой. Действительно, две грани построенного тела параллельны, а остальные грани пересекаются по параллельным прямым (Рис.1 ). Две грани призмы, параллельные между собой, называются ее основаниями, остальные грани называются боковыми гранями. 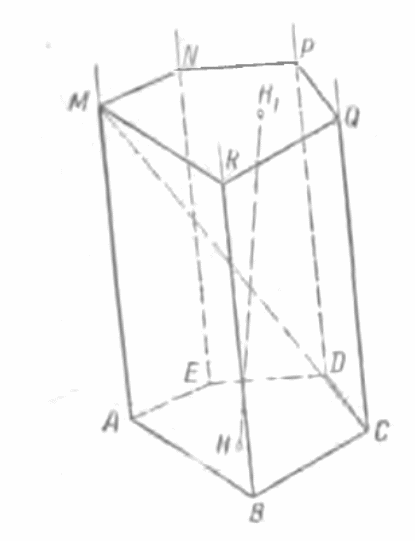 Рис. 1. Боковыми ребрами призмы называются ребра, по которым пересекаются ее боковые грани (AM, BR, CQ, . . .). Высотой призмы называется отрезок прямой, перпендикулярный к плоскостям ее оснований, заключенный между ними (НH1на Рис. 1). Виды призм. Призма называется треугольной, четырехугольной и т. д. в зависимости от того, какой многоугольник служит основанием призмы. Призма называется прямой, если ее боковые ребра перпендикулярны к плоскостям ее оснований. В противном случае призма называется наклонной. В прямой призме высота равна боковому ребру и боковыми гранями служат прямоугольники. Прямая призма, основаниями которой служат правильные многоугольники, называется правильной призмой. Параллелепипед. Параллелепипедом называется призма, основаниями которой служат параллелограммы.(Рис.2). Виды параллелепипедов. Параллелепипед, боковые ребра которого перпендикулярны к плоскостям оснований, называется прямым. В противном случае параллелепипед называется наклонным. В прямом параллелепипеде все боковые грани — прямоугольники. Прямоугольным параллелепипедом называется прямой параллелепипед, основания которого — прямоугольники. В прямоугольном параллелепипеде все грани—прямоугольники. Длины трех ребер прямоугольного параллелепипеда, сходящихся в одной вершине, называются его измерениями. Кубом называется прямоугольный параллелепипед, все три измерения которого равны между собой. Теорема 1. В параллелепипеде противоположные грани равны и параллельны. Дано: ABCDА1B1C1D1—параллелепипед (Рис. 2). Требуется доказать , что, например, грани АА1В1В и DD1C1C параллельны и равны. Доказательство. Так как все шесть граней параллелепипеда— параллелограммы, то AA1= DD1, А1В1 = D1C1, AA1//DD1и A1B1 //D1C1 . Следовательно, грани АА1В1В и DD1C1C параллельныв силу того, что две пересекающиеся прямые АА1и А1В1одной плоскости параллельны двум пересекающимся прямым DD1и D1C1 другой. (Если две пересекающиеся прямые, лежащие на одной плоскости, соответственно параллельны двум прямым, лежащим на другой плоскости, то эти плоскости параллельны.) Эти грани и равны, как двапараллелограмма, у которых, кроме указанного равенствасторон, и ∠АА1В1 = ∠DD1C1(углы, с соответственно параллельнымииодинаково направленными сторонами.) Теорема 2. Диагонали параллелепипеда пересекаются в одной точке и делятся в ней пополам. Дано: АС1, BD1, DB1и СА1—диагонали параллелепипеда ABCDA1 B1 C1 D1(Рис. 3). Требуется доказать, что АС1 , BD1 , DB1и СА1пересекаются в одной точке и делятся в этой точке пополам. Доказательство. Соединим точки А1с В и D1с С. Полученная фигура А1D1СВ —параллелограмм, так как стороны A1D1и ВС равны и параллельны. Диагонали А1С и BD1 параллелепипеда служат диагоналями полученного параллелограмма, следовательно, в точке пересечения О они делятся пополам. Точно так же, взяв одну из этих двух диагоналей, например диагональ BD1, и третью диагональ, например АС1, докажем, что они, являясь диагоналями параллелограмма AD1C1B, делятся в точке пересечения пополам. Следовательно, диагональ АС1проходит через ту же точку О—середину диагонали BD1. Наконец, так как DB1(четвертая диагональ) и АС1служат диагоналями параллелограмма ADC1 B1, то они, делясь в точке пересечения пополам, проходят через ту же точку О — середину диагонали АС1. Итак, все четыре диагонали параллелепипеда пересекаются в одной точке и делятся в этой точке пополам. 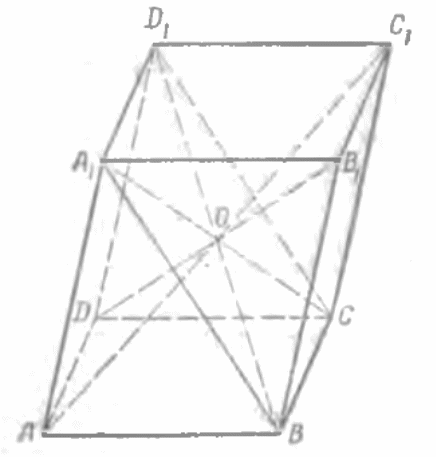 Рис. 3.  Рис.2. Пирамида. Пирамидой называется многогранник, ограниченный гранями многогранного угла и плоскостью, пересекающей все его грани (Рис. 4). Основанием пирамиды называется многоугольник, полученный в секущей плоскости (ABCDEF). В зависимости от числа сторон основания пирамиды могут быть треугольными, четырехугольными, пятиугольными и т. д. Треугольная пирамида обладает той особенностью, что каждую грань можно принять за основание пирамиды. Боковыми гранями пирамиды называются треугольники с общей вершиной S, называемой вершиной пирамиды. Боковыми ребрами пирамиды называются ребра, по которым пересекаются боковые грани, т. е. ребра SA, SB, . . ., выходящие из вершины пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания. Правильной пирамидой называется пирамида, основанием которой служит правильный многоугольник, и высота которой проходит через центр этого многоугольника. Все боковые ребра правильной пирамиды равны (как наклонные, основания которых равно удалены от основания перпендикуляра); все боковые грани — равные равнобедренные треугольники (как имеющие по три соответственно равные стороны). Апофемой правильной пирамиды называется высота боковой грани, опущенная из вершины пирамиды. Правильная треугольная пирамида, боковое ребро которой равно стороне основания, носит название тетраэдра. 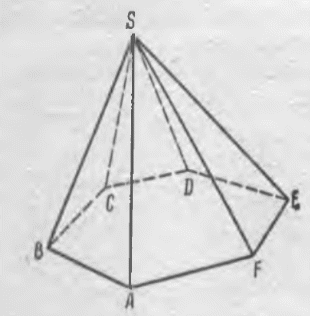 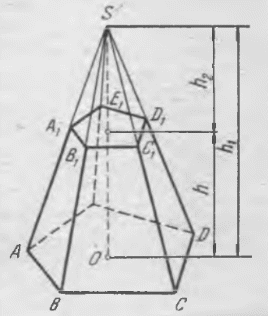 Рис. 4. Рис.5. Усеченной пирамидой (ABCDEA1B1С1D1E1) называется часть пирамиды (SABCDE), заключенная между ее основанием и секущей плоскостью, параллельной основанию (Рис. 5). Основаниями усеченной пирамиды называются ее параллельные грани (ABCDE и A1В1C1D1Е1). Нижним основанием называется основание исходной пирамиды (ABCDE); верхним основанием называется многоугольник, лежащий на секущей плоскости (A1B1C1D1E1). Высотой усеченной пирамиды, называется перпендикуляр, опущенный из какой-нибудь точки верхнего основания на нижнее. Правильной усеченной пирамидой называется такая усеченная пирамида, у которой основания — правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна к плоскости оснований. §3. Свойства многогранников и круглых тел. 1.Два равных многогранника имеют один и тот же объем, независимо от их расположения в пространстве. 2. Объем многогранника, представляющего собой сумму двух смежных многогранников, равен сумме объемов этих многогранников. 3. Если из двух многогранников первый содержится целиком внутри второго, то объем первого многогранника не превосходит объема второго. Многогранники, имеющие равные объемы, называются равновеликими. За единицу объема принимается объем куба, ребро которого равно единице длины (мм, см, дм, м и т.п.). §4. Теорема Эйлера. Пусть е – число вершин,f – число граней, k – число ребер данного многогранника. Число е + f – k называется эйлеровой характеристикой многогранника. Имеет место следующая замечательная теорема. Теорема 1. Эйлерова характеристика всякого многогранника нулевого рода равна двум, т. е. е + f – k = 2. Доказательство этой теоремы следует из теоремы: эйлерова характеристика всякой односвязной многогранный поверхности равна единице, т.е. е + f – k = 1. В самом деле, пусть Ф – данный многогранник, имеющий е вершин, f граней, k ребер. Если отбросить одну из граней этого многогранника, то согласно теореме: каждая из двух многогранных поверхностей, на которые произвольный разрез делит многогранник нулевого рода, односвязна получим односвязную многогранную поверхность, имеющую е вершин, (f – 1) граней и k ребер. В силу теоремы 1 имеем: е + (f - 1) – k = 1, или е + f – k = 2. Впервые это свойство установил Эйлер, его именем и названа теорема. |
