Курсовая работа Объем многогранников. Объем многогранников .. Курсовая работа Научный руководитель доцент, к п. н. Кузина Наталья Георгиевна Ульяновск, 2014 Содержание

• Название: Курсовая работа Научный руководитель доцент, к п. н. Кузина Наталья Георгиевна Ульяновск, 2014 Содержание
• Анкор: Курсовая работа Объем многогранников
• Дата: 16.08.2022
• Размер: 0.71 Mb.
• Имя файла: Объем многогранников ..docx
• Тип: Курсовая; #646895
• страница: 3 из 3

§2. Объем призмы.

1. 
   Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы.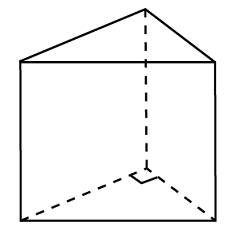
   

Решение:

Объем призмы вычисляется по следующей формуле: V=S_o∙H (H – высота, в данном случае и боковое ребро прямой призмы).

При этом в основании – прямоугольный треугольник, площадь которого находится как полупроизведение катетов:

S_o=1/2∙ 4∙ 6=12;

Тогда V=12∙ 5=60.

Ответ: 60.

2. 
   В сосуд, имеющий форму правильной треугольной призмы, налили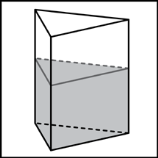
   

1300 см³  воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 28 см. Найдите объем детали. Ответ выразите в см³.

Решение: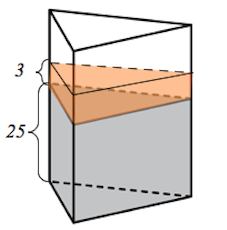

Объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен объему прямой призмы с высотой 3 и основанием, равным основанию исходной призмы. То есть объем вытесненной жидкости составляет 3/25 объема жидкости.

Итак, объем детали есть 3/25∙1300 = 156 см³.

3. 
   Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 19,5. Найдите объем исходной призмы.
   

Решение: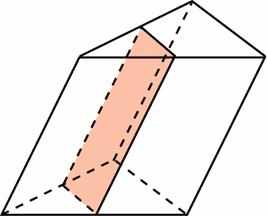

Так как плоскость проведена через среднюю линию основания, то площадь основания отсеченной  призмы меньше площади основания исходной в 4 раза  (основания (как треугольники)) подобны друг другу с коэффициентом подобия 2, значит площади находятся в отношении 

2² = 4).

Высоты призм совпадают.

Поэтому объем исходной призмы в 4 раза больше объема отсеченной призмы, то есть равен 19,5∙4 = 48.

Ответ: 78.

§3. Объем параллелепипеда.

1. 
   Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6. Найдите объем параллелепипеда.
   

Решение:

Высота прямоугольного параллелепипеда равна высоте цилиндра,

то есть 6. Раз основание цилиндра вписано в основание прямоугольного параллелепипеда, то в основании параллелепипеда – квадрат. И поскольку радиус основания цилиндра равен 6, то  стороны основания прямоугольного  параллелепипеда равны 12.

Итак, V = 6∙12∙12 = 864.

Ответ: 864.

2. 
   Площадь грани прямоугольного параллелепипеда равна 21. Ребро, перпендикулярное этой грани, равно 3. Найдите объем параллелепипеда.
   

Решение:

Объем V прямоугольного параллелепипеда (прямой призмы) равен V=S_o∙H (H – высота призмы, в данном случае ребро, перпендикулярное грани, площадь которой известна ).

Поэтому, V = 21∙3 = 63.

Ответ: 63.

§4. Объем пирамиды.

1. 
   Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?
   

Решение:

Так как объем пирамиды вычисляется по формуле V = (S_o∙H)/3, то при увеличении

высоты в 2 раза (только высоты) мы получим вдвое больший объем пирамиды.

Ответ: 2.

2. 
   От треугольной призмы, объем которой равен 129, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
   

Решение:

Объем призмы есть S_o∙ H, объем пирамиды есть (S_o∙ H)/3 (основания и высоты одинаковы). То есть объем отсеченной пирамиды есть 1/3объема призмы, а именно 129/3=43. Тогда объем оставшейся части равен 129-43=86.

Ответ: 86.

§4. Объем шара.

1. 
   Площадь большого круга шара равна 1. Найдите площадь поверхности шара.
   

Решение:

Радиус большого круга – радиус шара. Поэтому 1=πR²;

Площадь поверхности шара вычисляется по формуле S=4π R².

Поэтому S=4∙1=4.

Ответ: 4.

2. 
   Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 28 раз?
   

Решение:

Площадь поверхности шара вычисляется по формуле S=4πR².

Увеличение радиуса R в 28 раз влечет за собой увеличение объема шара в 28², то есть в 784 раза.

Ответ: 784.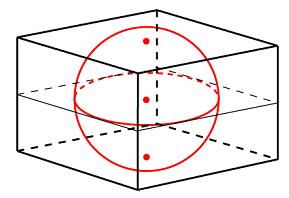

3. 
   Объем прямоугольного параллелепипеда, описанного около сферы, равен 10648. Найдите радиус сферы.
   

Решение: Прямоугольный параллелепипед, описанный вокруг сферы, является кубом. Поэтому 10648=a³, где a –

ребро куба. Откуда a=22.

При этом радиус сферы есть a/2.

Значит радиус сферы есть R=a/2=11.

Ответ: 11.

Заключение.

Трудно переоценить значение темы «Многогранники» не только в самой геометрии, но и других науках, в повседневной жизни. Без знания закономерностей, связанных с этими геометрическими телами, невозможно было бы дальнейшее изучение геометрии, развитие архитектуры, астрономии, физики.

В ходе выполнения работы, познакомились с происхождением терминов, связанных с многогранниками. Рассматривая уже знакомые свойства, изучали новые, ранее неизвестные, но весьма полезные при решении задач.

Работа носит исследовательский характер. Ее можно использовать в качестве дополнительного материала при изучении темы «Объем многогранников». Все изложенные факты иллюстрируются рисунками, чертежами, которые облегчают их понимание и запоминание.

Литература.

1. 
   Александров П. С., Маркушевич А. И., Хинчин А. Я Энциклопедия элементарной математики – М.: Наука, 1966
   
2. 
   Андреев П. П., Шувалова Э. З. Геометрия – М.: Наука, 1966
   
3. 
   Аргунов Б. И., Балк М. Б. Элементарная геометрия – М.: Просвещение, 1998
   
4. 
   Атанасян Л. С., Бутузов В. Ф. Геометрия 10-11- М.: Просвещение, 1993
   
5. 
   Атанасян Л. С., Базылев В. Т. Геометрия Ч. 2 – М.,2011
   
6. 
   Атанасян Л. С. Геометрия Ч.1 – М.: Просвещение, 1973
   
7. 
   Гусев В. А., Литвиненко В. Н., Мордкович А. Г. Практикум по элементарной математике (геометрия) – М.: Просвещение, 1992
   
8. 
   Ляпин М. П. Сборник задач по элементарной математике
   

( с решениями) – Издательство Казанского Университета, 1975

9. 
   Сабитов И. Х., М. Берже Геометрия Т. 1 – М.: Мир, 1984
   
10. 
    http://www.egemaximum.ru
    
11. 
    http://www.reshuege.ru
    
12. 
    http://www.referatbank.ru