Курсовая работа Объем многогранников. Объем многогранников .. Курсовая работа Научный руководитель доцент, к п. н. Кузина Наталья Георгиевна Ульяновск, 2014 Содержание
 Скачать 0.71 Mb.
|
|
Глава 2. Объемы многогранников и круглых тел. §1. Объем геометрических фигур. 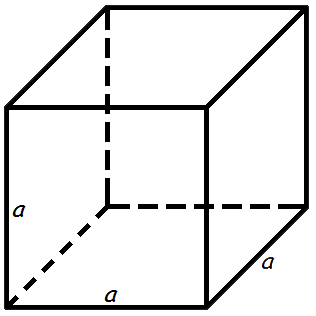 Объем куба. Объем куба равен кубу длины его грани.Формула объема куба: V = a3, где V- объем куба, а - длина грани куба. Объем призмы. Объем призмы равен произведению площади основания призмы, на высоту. 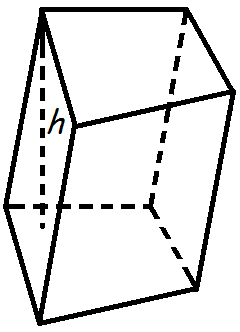 Формула объема призмы: V = Sо h, где V - объем призмы, Sо - площадь основания призмы, h - высота призмы. Объем параллелепипеда. Объем параллелепипеда равен произведению площади основания на высоту. 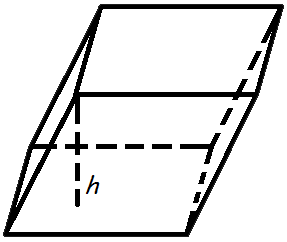 Формула объема параллелепипеда: V = Sо · h, где V - объем параллелепипеда, Sо - площадь основания, H - длина высоты. Объем прямоугольного параллелепипеда. Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. Формула объема прямоугольного параллелепипеда: 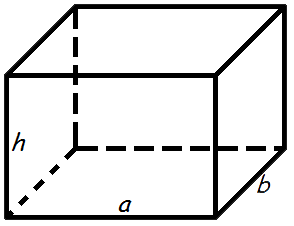 V = a · b · h, где V - объем прямоугольного параллелепипеда, а- длина, b- ширина, h - высота.
Формула объема пирамиды: где V - объем пирамиды, 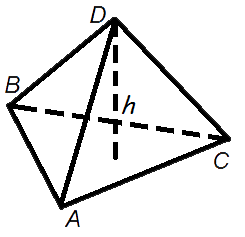 Sо - площадь основания пирамиды, h - длина высоты пирамиды. Объем цилиндра. Объем цилиндра равен произведению площади его основания на высоту. 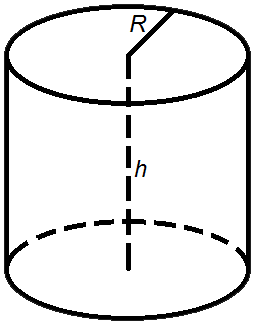 Формулы объема цилиндра:V = π R2 h V = Sо h, где V - объем цилиндра, Sо - площадь основания цилиндра, R - радиус цилиндра, h - высота цилиндра, π = 3,141592
Формулы объема конуса:
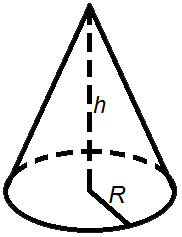 где,V - объем конуса, Sо - площадь основания конуса, R - радиус основания конуса, h- высота конуса, π = 3,141592 Объем шара. Объем шара равен четырем третьим от его радиуса в кубе умноженного на число пи.
, где 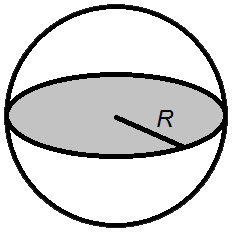 V - объем шара, R - радиус шара, π = 3.141592 . §2. Различные подходы к определению объема многогранников. Задача определения объемов тел относится к глубокой древности. Она возникла в связи с практической деятельностью людей. Говоря простым языком, объем - это часть пространства, занимаемая телом. Точнее: объем - некоторая физическая, а именно геометрическая величина, характеризующая то свойство тел, что они трехмерны или занимают часть пространства. С понятием величины много раз можно встретиться в физике и в геометрии. Прежде всего, величины можно измерять, получая при этом именованные числа. Считается, что величина, или именованное число, которое ее выражает, - это одно и то же. Тогда: 1) величина не может принимать отрицательных значений; 2) если тело (или носитель величины) разбито на части, то сумма величин частей равна величине целого. Величины одного рода можно складывать; 3) для двух величин одного рода существует отношение - отвлеченное число, которое не зависит от способа измерения величин . Рассмотрим конкретный пример. Представим себе два сосуда: один в форме куба, а второй произвольной формы . Пусть оба сосуда доверху наполняются жидкостью. Допустим, выяснилось, что для наполнения первого сосуда понадобилось m кг жидкости, а для наполнения второго сосуда понадобилось n кг жидкости. Естественно считать, что второй сосуд в раз больше первого. Число, указывающее, во сколько раз второй сосуд больше первого, мы будем называть объемом второго сосуда. Первый сосуд является единицей измерения. Из этого определения понятия объема получаются следующие его свойства: · Во-первых, так как для заполнения каждого сосуда требуется определенное количество жидкости, то каждый сосуд имеет определенный (положительный)объем. · Во-вторых, для заполнения равных сосудов потребуется одно и то же количество жидкости. Поэтому равные сосуды имеют равные объемы. · В-третьих, если данный сосуд разделить на две части, то количество жидкости, необходимое для заполнения всего сосуда, состоит из количества жидкости, необходимой для заполнения его частей. Поэтому объем всего сосуда равен сумме объемов его частей. По данному определению для того, чтобы узнать объем сосуда, надо заполнить его жидкостью. В жизни, однако, требуется решать обратную задачу. Требуется узнать количество жидкости, необходимой для заполнения сосуда, не производя самого заполнения. Если знать объем сосуда, то количество жидкости можно получить, умножая объем сосуда на количество жидкости, необходимой для заполнения единицы объема. Тело можно называть простым, если его можно разбить на конечное число тетраэдров, то есть треугольных пирамид. В частности, такие тела как призма, пирамида, вообще выпуклый многогранник, являются простыми. Рассмотрим другое определение объема многогранников. Число, характеризующее величину внутренней области многогранника, называется объемом многогранника. Смежными многогранниками называются такие многогранники, которые имеют одну или несколько общих граней, причем остальные точки каждого из многогранников расположены вне другого. Существуют два подхода к определению объема: 1 подход. Понятие объема вводится аксиоматически. Объем - это положительная величина, численное значение которой обладает следующими свойствами: - равные тела имеют равные объемы; - если тело разбито на части, являющиеся простыми телами, то объем этого тела равен сумме объемов его частей; - объем куба, ребро которого равно единице длины, равен единице. 2 подход. Понятие вводится конструктивно. Считается, что каждое из рассматриваемых тел имеет объем, который можно измерить с помощью выбранной единицы измерения объемов. За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см. называют кубическим сантиметром и обозначают см3. §3. Объем многогранника в евклидовом пространстве. 1.Понятие объема многогранника в евклидовой геометрии вводится таким же путем, как и понятие площади многоугольника. По аналогии с теорией площадей многоугольников вводится понятие суммы двух многогранников: F = F1 + F2. Разложение многогранника F на сумму многогранников F1 и F2производится с помощью какой – либо многогранной поверхности G, причем F1∩F2 = G, а FUF2 = F. Под многогранной поверхностью понимается связная часть поверхности какого – либо многогранника, образованную некоторыми из его граней. Если обозначить М - множество всех многогранников евклидова пространства, то можно сказать, что установлено измерение объемов многогранников, если определено отображение V : М →  *+ ,удовлетворяющее следующим аксиомам: если многогранникиF и F’ равны, то V(F) = V(F’); если F = F1 + F2, то V(F) = V(F1) + V(F2); V(P0) = 1, где P0 - куб, ребро которого равно единичному отрезку. Положительное число V(F) называется мерой или объемом многогранника F. По аналогии с теорией измерения площадей можно доказать следующие теоремы. Теорема 1. В евклидовом пространстве существует хотя бы одно отображение V : M → *+ , удовлетворяющее аксиомам 1,2 и 3 измерения объемов многогранников.Теорема 2. Если выбран единичный отрезок, то существует не более одного отображения V : М → *+ , удовлетворяющее аксиомам 1,2 и 3 измерения объемов многогранников.Теорема 3. Если V : М → *+ - отображение, удовлетворяющее аксиомам 1,2 и 3 измерения объемов многогранников, то V(P) = xyz, где P – прямоугольный параллелепипед с измерениями x,y,z.С помощью этой теоремы так же можно вывести формулы для вычисления объемов простейших многогранников – прямой и наклонной призм, пирамид и других многогранников. 2. Два многогранника называются равновеликими, если их объемы равны. Ясно, что равновеликость есть отношение эквивалентности на множестве М всех многогранников. Два многогранника F и F’называются равносоставленными, если их можно разложить на одно и то же число соответственно равных многогранников. Два равносоставленных многогранника являются, очевидно, и равновеликими. Но в отличие от теории площадей обратное утверждение, вообще говоря, неверно: не любые два равновеликих многогранника будут и равносоставленными. Немецкий математик М. Ден в 1900 г. Доказал следующую теорему. Теорема 4. Пусть α1,α2, …, αr – меры двухгранных углов многогранника Р, а β1, β2, …, βs – меры двухгранных углов многогранника Р’. Если многогранники Р и Р’ равносоставлены, то существуют такие целые положительные числа m1, m2, …, mr и n1,n2, …, ns и такое целое (положительное, отрицательное или равное нулю) число c, что m1α1 + m2α2 + … αr mr - (n1β1 + n2β2 +… nsβs) = πc. (1) Эта теорема выражает необходимые условия равносоставленности двух равновеликих многогранников. В 1965 г. французский математик Сидлер доказал, что условия Дена являются достаточными. Существуют равновеликие многогранники, для которых условие (1) не выполняется. В 1901 г. Ден также доказал, что для куба и равновеликого ему правильного тетраэдра условие (1) не выполняется, поэтому они не равносоставлены. Более того, можно доказать, что равновеликие тетраэдры, вообще говоря, не равносоставлены. Вследствие этого применение теории пределов (в той или иной форме) при изменении объема пирамиды является неизбежным. §4. Принцип Кавальери. Для нахождения объемов тел в ряде случаев удобно пользоваться теоремой, получившей название принцип Кавальери. Этот принцип был сформулирован итальянским математиком Кавальери в его книге «Геометрия, изложенная новым способом при помощи неделимых частей непрерывных величин», вышедшей в 1635 г. Кавальери занимался вопросом нахождения отношения объемов двух тел, «суммируя все плоские сечения», которые образуются в обоих телах рядом параллельных плоскостей, и впервые высказал во всей общности предложение, которое носит название принципа Кавальери : если два тела могут быть помещены в такое положение, при котором любая плоскость, параллельная какой-нибудь данной плоскости и пересекающая оба тела, дает в сечении с ними равновеликие фигуры, то объемы таких тел одинаковы. Глава 3.Тематические задачи . §1. Объем цилиндра. 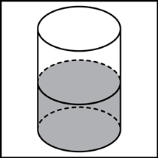 В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см .Решение: Объем вытесненной жидкости равен объему погруженной детали в жидкость. Первоначально жидкость занимала объем V = So∙12. И так как объем жидкости по условию равен 1200 см3  , то1200 = So∙12; So=100. Тогда объем вытесненной жидкости (а значит и детали) есть V det = So ∙10 = 100∙10 = 1000 см3 . Ответ: 1000. В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,4 раза. Чему равен объем детали? Ответ выразите в литрах. 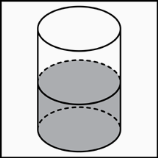 Решение:Объем вытесненной жидкости – и есть объем детали. Объем вытесненной жидкости равен 1,4 исходного объема (если допустить, что первоначальная высота столбика жидкости равна H, то новая высота столбика – 2,4 H , то есть разница – 1,4 H), поэтому объем детали равен 1,4 от исходного объема, то есть 1,4 ∙10 = 14 литрам. Ответ: 14. 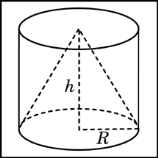 Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27.Решение: Объем конуса есть So∙H/3 объем же цилиндра есть So∙H , поэтому объем данного цилиндра втрое больше объема конуса и он равен 27∙3 , то есть 81. Ответ: 81. 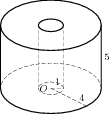 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите 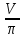 . Решение: V = π∙42∙5 - π∙12∙5 = 40π - 5π = 75π. 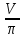= 75.Ответ: 75. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажит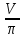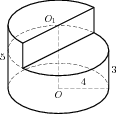е . Решение: V = π∙42∙3 + (π∙42∙2)/2 = 48π +16π = 64π. 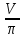= 64.Ответ: 64. |