КУРСОВАЯ РАБОТА по аэромеханике самолета DС-9. Курсовая Работа_DC-9-30. Курсовая работа по аэромеханике
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
2 РАСЧЕТ КРИТИЧЕСКОГО ЧИСЛА МАХА САМОЛЕТАКритическое число Маха – есть такое число Маха набегающего потока, при котором где-либо на профиле (теле) возникает скачок уплотнения. За расчетное критическое число Маха самолета принимается самое минимальное значение критического числа Маха отдельных агрегатов самолета (крыло, фюзеляж, оперение и др.). 2.1 Расчет критического числа Маха крыла и оперения Критическое число Маха крыла будем определять из уравнения: 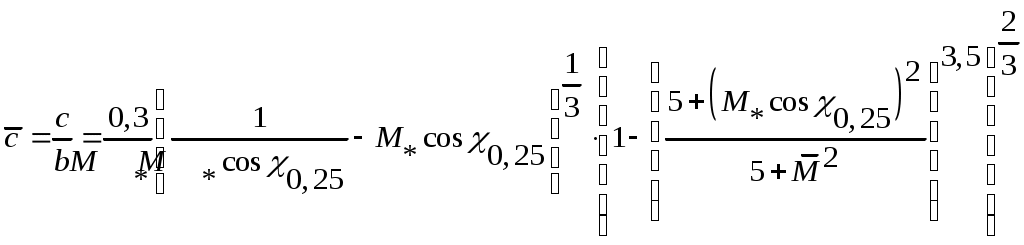 (2.1) (2.1)где где  Выбираем Для крылаПодставляя различные числа Маха в уравнение (2.1) добиваемся того, чтобы относительная толщина профиля была равна заданной:  тогда критическое число Маха для крыла Для вертикального оперения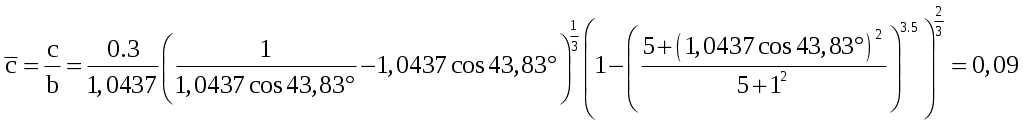 При Тогда Для горизонтального оперения 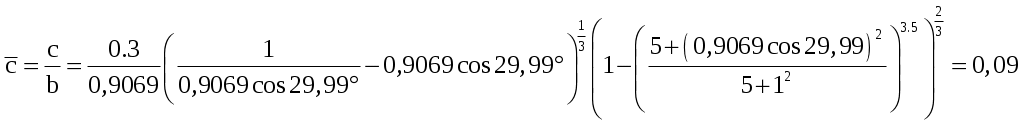 тогда для горизонтального оперения 2.2 Расчет критического числа Маха для фюзеляжа и мотогондолы Критическое число Маха для фюзеляжа с параболической формой носовой части определяем по формуле где Удлинение носовой части фюзеляжа определим из соотношения где Тогда Расчет критического числа Маха мотогондолы ведется аналогично фюзеляжу с эллиптической формой носовой части, с заменой удлинения носовой части фюзеляжа на удлинение носовой части мотогондолы. где где Тогда 2.3 Оценка числа Маха За критическое число Маха всего самолёта Получили: Наименьшим числом Маха является число Маха крыла. Принимаем критическое число Маха самолёта 2.4 Определение расчетной скорости самолета Для скоростных самолётов с ТРД за расчётную скорость принимают скорость полёта, соответствующую критическому числу Маха самолёта где На высоте 12000м, 3 Расчет полетной докритической поляры 3.1 Уравнение докритической поляры Докритическую поляру самолета будем строить для расчетной высоты полета H=12000 м и расчетной скорости Уравнение докритической поляры имеет вид cxa=cxamin+A(cya-cyaисх)2, где A – коэффициент отвала поляры определяется по формуле: A=1/π·λэф, где λэф эффективное удлинение крыла определяется как 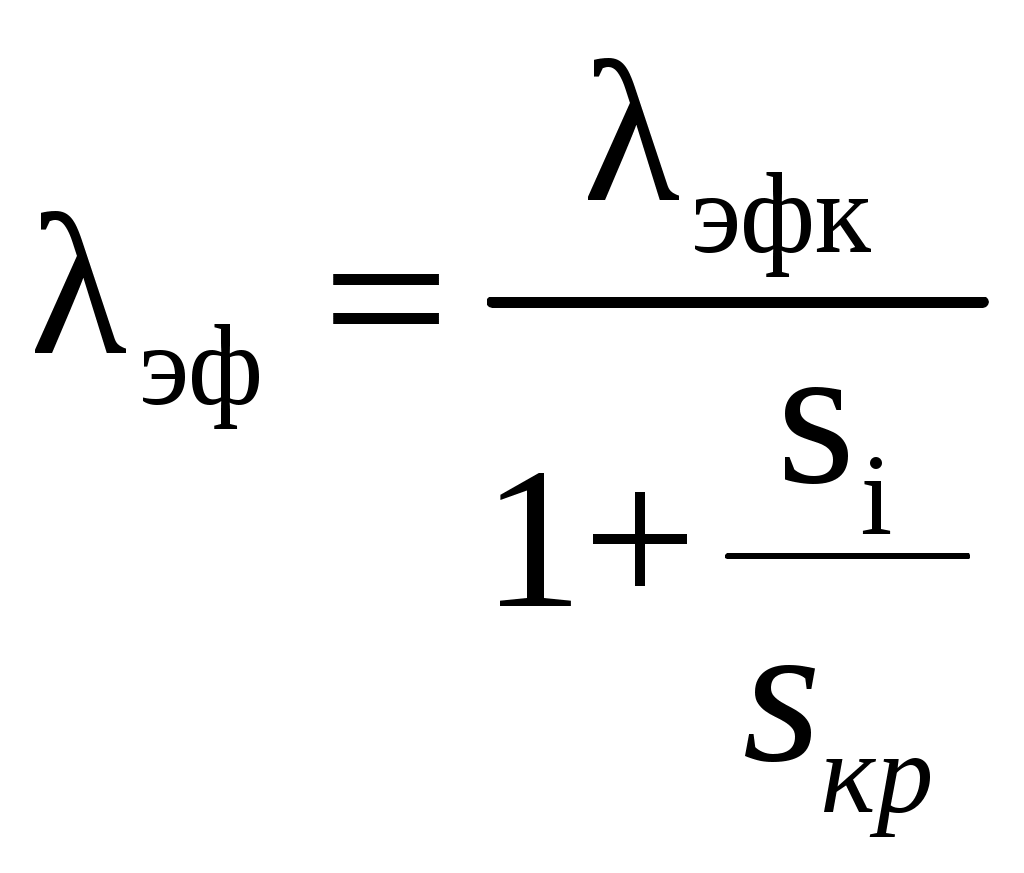 , , где si – площадь крыла, занятая фюзеляжем; λэфк – эффективное удлинение крыла, определяемое в зависимости от удлинения крыла λ, сужения крыла η и стреловидности крыла по передней кромке где 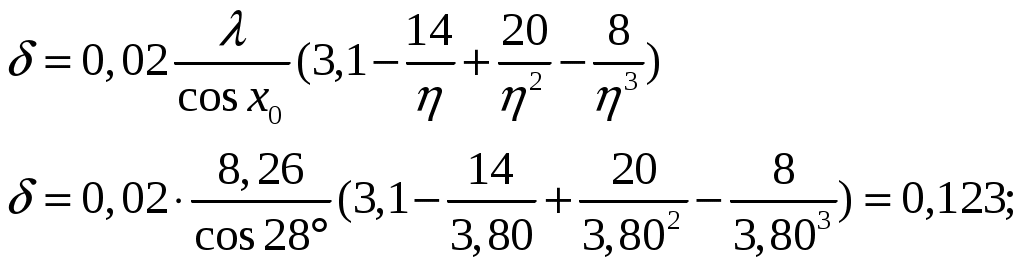 (3.2) (3.2)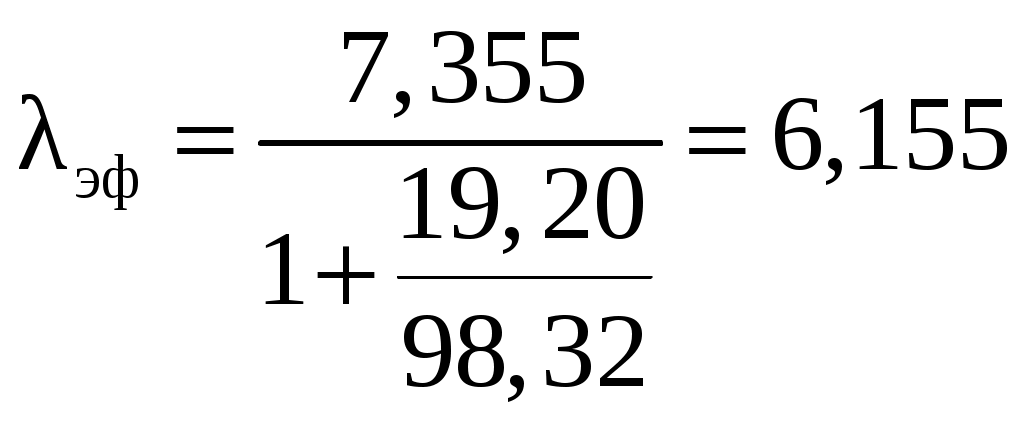 ; ;3.2 Определение коэффициента минимального лобового сопротивления Минимальное сопротивление самолета определяется по формуле: 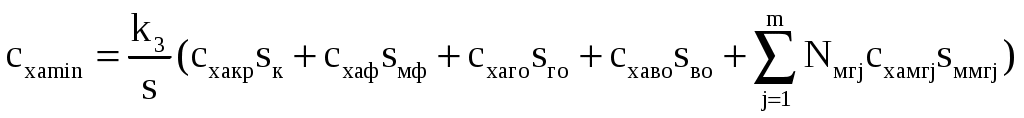 ; (3.4) ; (3.4)где к3 – коэффициент запаса, учитывающий неучтенные данные методикой факторы и принимаемый равным 1,05; сxaкр, cxaф, сxaго, сxaво, сxaмг – коэффициенты минимального лобового сопротивления крыла, фюзеляжа, горизонтального, вертикального оперения и одной мотогондолы соответственно; m – количество типов мотогондол на самолете; Nмгj – количество мотогондол двигателя данного типа; s, sк, sмф, sго, sво, sммгj – площадь крыла, площадь консолей крыла, характерные площади фюзеляжа, горизонтального, вертикального оперения и одной мотогондолы данного типа. 3.2.1 Определение коэффициента минимального лобового сопротивления для крыла Крыло самолета заменяем эквивалентной плоской пластиной размахом, равным размаху крыла самолета l=28.5м и средней хордой bср: bср= Определяем число Рейнольдса для крыла: где vрасч – расчетная скорость, м/с; bср – средняя хорда крыла, м; υ(h) – кинематическая вязкость воздуха на расчетной высоте полета, м2/с. υ(h)=4.574 Т.к. Коэффициент профильного сопротивления крыла подсчитывается как сxaр=k1·cf·ηc·ηм, где к1 – коэффициент, учитывающий долю поверхности крыла, закрытой мотогондолой, определяется по формуле: sк –площадь консолей крыла; cf – коэффициент сопротивления трения плоской пластины в несжимаемом потоке; ηс и ηм – коэффициенты, учитывающие влияние на профильное сопротивление толщины профиля и числа M∞, соответственно. к1=2. Для турбулентного пограничного слоя 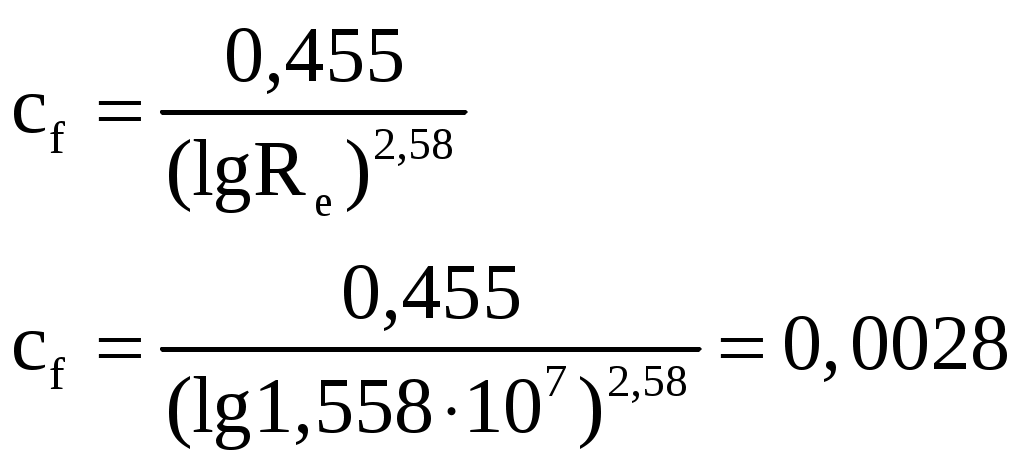 ; (3.6) ; (3.6)коэффициент ηс зависит от относительной толщины профиля и положения точки перехода коэффициент ηм определяем по рис. 3.5. [1]: ηм=0.97; Сxaр=2·0.0028·1.456·0.97=0.0079. Коэффициент минимального лобового сопротивления крыла учитывает взаимное влияние крыла и фюзеляжа и наличие щелей: где кинт – коэффициент интерференции между крылом и фюзеляжем, зависит от положения крыла относительно фюзеляжа. Для схемы, низкоплан kинт=0.75. Sпф=19.20м2, lз=16.24м, lэ=7.34м, lпр=0, lи=14.67м; 3.2.2 Определение коэффициента минимального лобового сопротивления горизонтального оперения Расчет минимального лобового сопротивления горизонтального и вертикального оперения производим так же, как для крыла. bсрГО= сxaрго=k1·cf·ηc·ηм, где k1=2; ηc=1.25; ηм=0.97; сxaрго=2·0.003·1.25·0.97=0.0073 где кинт=0,75; Sпф=0; 3.2.3 Определение коэффициента минимального лобового сопротивления для вертикального оперения bср= сxaрво=k1·cf·ηc·ηм, где k1=2; ηc=1.25; ηм=0.97; сxaрво=2·0.0027·1.25·0.97=0.0066 где кинт=0,375; Sпф=0; 3.2.4 Определение коэффициента минимального лобового сопротивления фюзеляжа и мотогондол Для фюзеляжа с заострённой носовой и кормовой частью при докритических скоростях основной составляющей сопротивления является сопротивление трения . Коэффициент сопротивления асимметричного фюзеляжа (мотогондолы) или эквивалентного тела вращения определяем по аналогии с сопротивлением трения плоской пластины: где ηλ – коэффициент, учитывающий отличие формы фюзеляжа от плоской пластины; ηм – коэффициент, учитывающий сжимаемость потока; Fом – омываемая поверхность фюзеляжа; sмф – площадь миделя фюзеляжа. Коэффициент Сопротивления мотогондол двигателя определяется также как и для фюзеляжа 2 Определим коэффициент минимального лобового сопротивления всего самолёта: 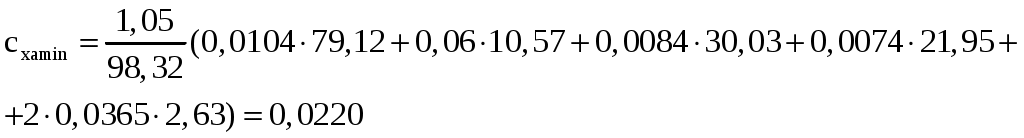 Таким образом, уравнение докритической поляры (рисунок 1) будет иметь вид: cxa=0,022+0,052·(сya-0,336)2 (3.9) Расчет координат оформим в виде таблицы (таблица1).
Таблица 1- Координаты точек докритической поляры 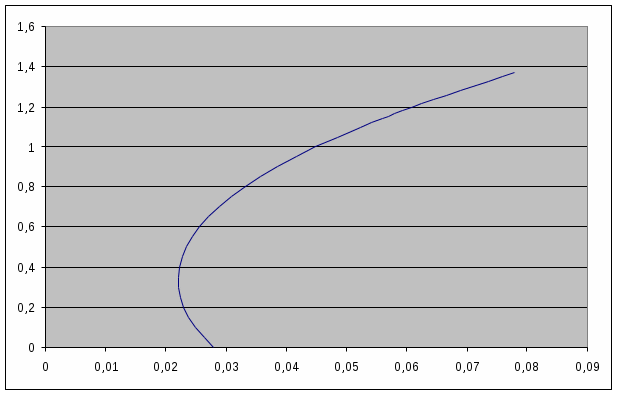 Рисунок 1 – Докритическая поляра 4 Расчёт закритических поляр самолёта При числах Маха больше критического Общее сопротивление самолёта является суммой сопротивлений, соответствующих докритическим скоростям полёта и волновых; Каждому числу М Волновое сопротивление Будем считать, что индуктивно-волновое сопротивление создаёт только крыло, при его определении коэффициент подъёмной силы берётся в диапазоне от 0 до 0,6 с шагом 0,1 Остальные элементы создают только пассивное волновое сопротивление и при их расчёте принимается Значения Коэффициент пассивного волнового сопротивления самолёта при где S, SГО, SВО, Sмф, SМГо - площади крыла, горизонтального и вертикального оперения, миделя фюзеляжа и мотогондол двигателей j-того типа соответственно. Определяем коэффициенты волнового сопротивления крыла, горизонтального и вертикального оперения с помощью формул, исходя из условия: Если 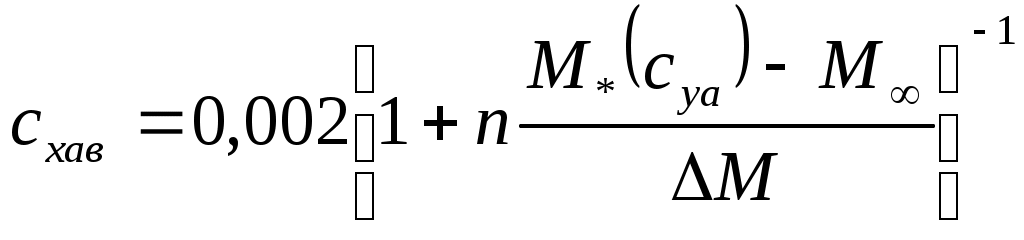 (4.4) (4.4)Если 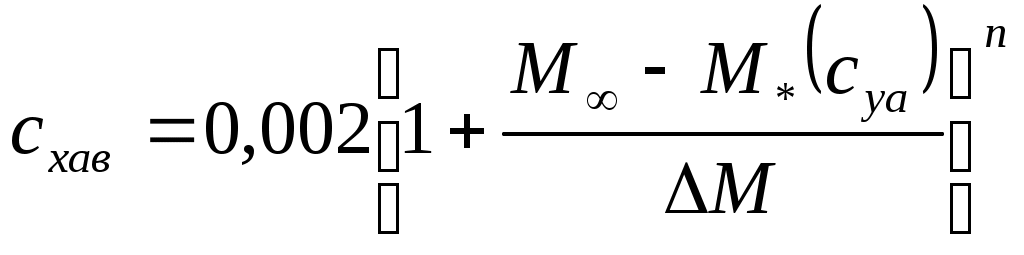 (4.5) (4.5)где М и n эмпирические константы равные М=0,05 и n=2,5. Коэффициент пассивного волнового сопротивления фюзеляжа вычисляется по формуле: 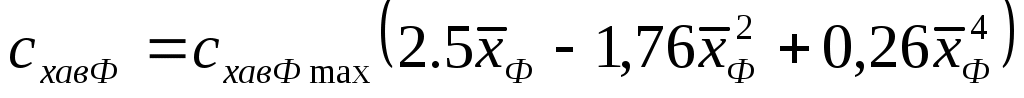 (4.6) (4.6)где максимальный коэффициент волнового сопротивления фюзеляжа 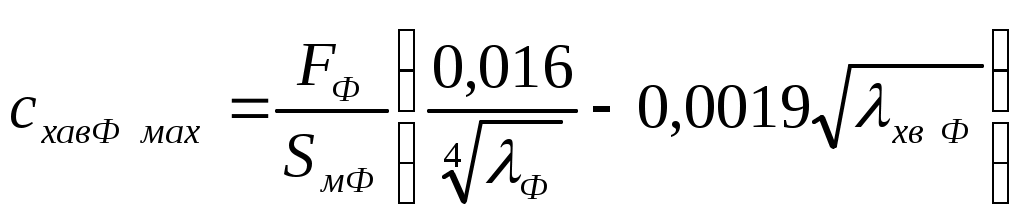 (4.7) (4.7)где Коэффициент волнового сопротивления мотогондол рассчитывается также, как и Имеем критические числа Маха, определённые в разделе 2: С помощью формулы (2.1) определим критические числа Маха для крыла с различным
Таблица 2 - Критические числа Маха для крыла Для каждого из чисел Маха ряда: 0,7;0,75; 0,8; 0,85; 0,9; 0,95 рассчитаем зависимость коэффициента подъёмной силы от коэффициента силы лобового сопротивления, и результаты оформим в виде таблицы (таблица 4). Закритические поляры представлены на рисунке 2. Для
Для
Для
Для
Для
Для
Таблица 3 – Координаты закритических поляр 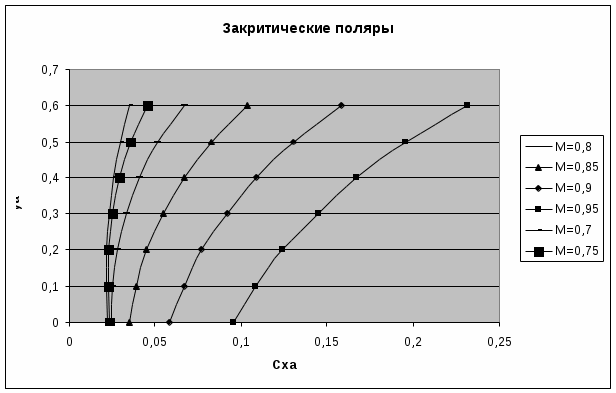 Рисунок 2 – Закритические поляры |
