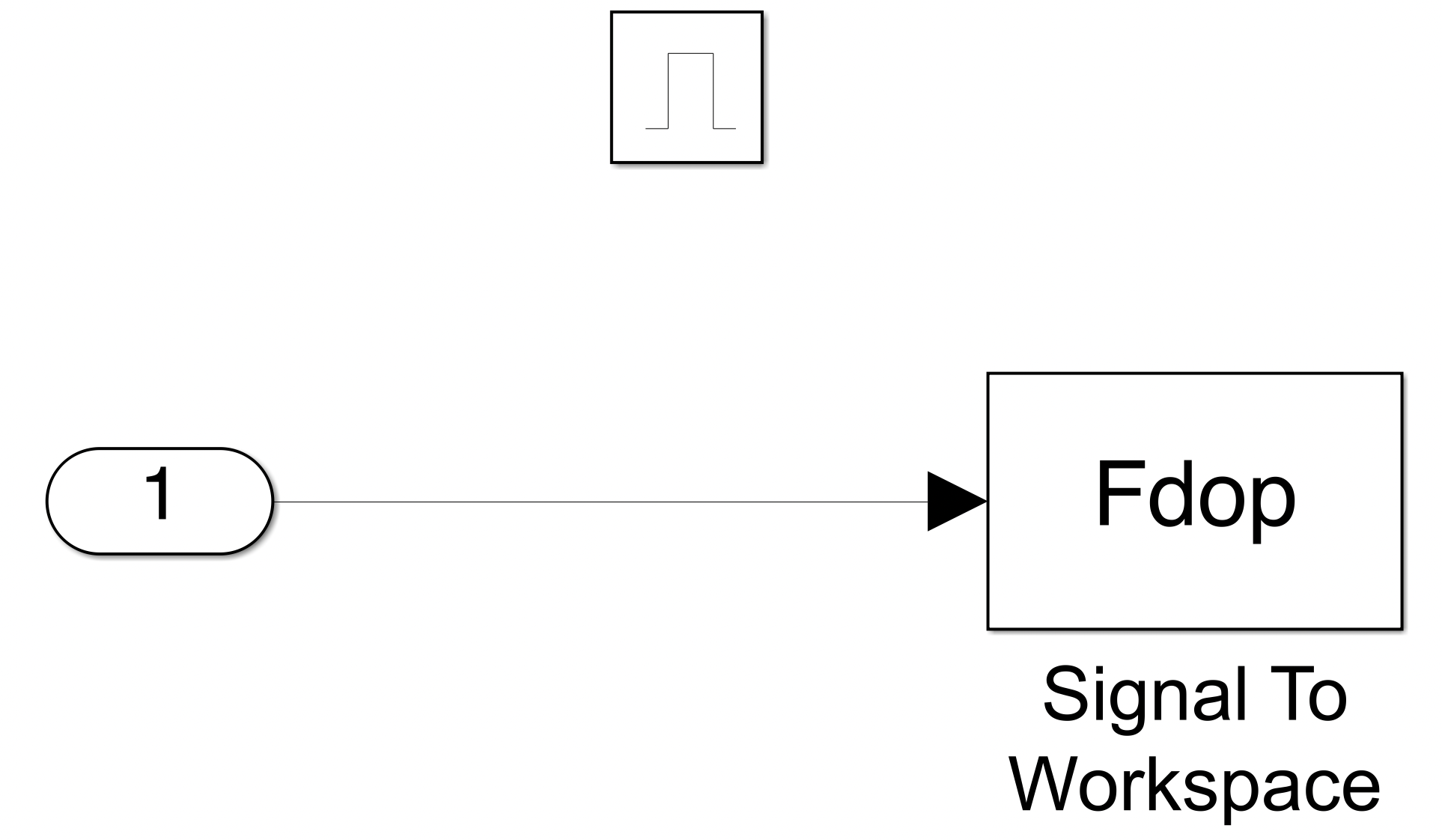
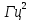Флуктуационные ошибки оценки доплеровской частоты эхо-сигнала подводного объекта. Курсовая работа по дисциплине Алгоритмы оценки параметров и классификации объектов Первая часть курсовой работы Флуктуационные ошибки оценки доплеровской частоты эхосигнала подводного объекта
 Скачать 2.29 Mb. Скачать 2.29 Mb.
|
|
МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный морской технический университет» (СПбГМТУ) кафедра морских информационных систем и технологий Курсовая работа по дисциплине: «Алгоритмы оценки параметров и классификации объектов» Первая часть курсовой работы – «Флуктуационные ошибки оценки доплеровской частоты эхо-сигнала подводного объекта» Вторая часть курсовой работы – «Исследование классификационной способности признаков при распознавании объектов» 2 вариант
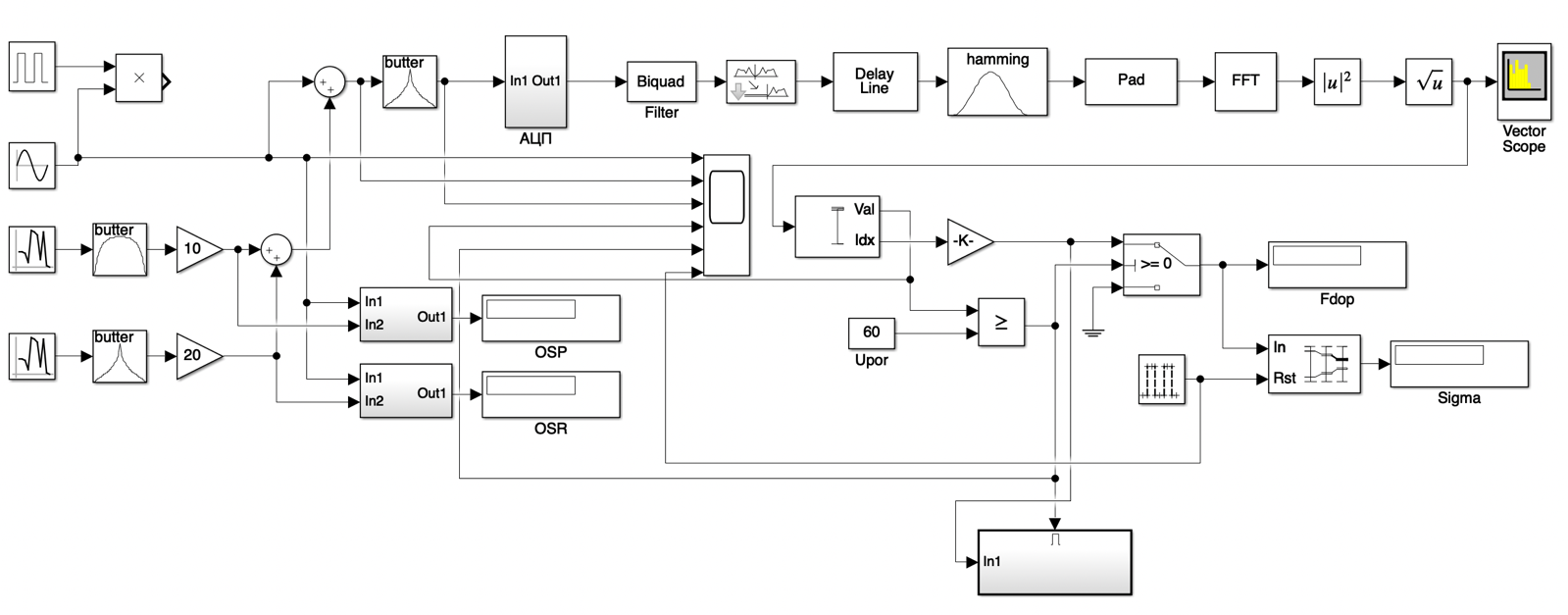
Санкт-Петербург 2021 Содержани Часть 1. Флуктуационные ошибки оценки доплеровской частоты эхо-сигнала подводного объекта 3 2.Расчет параметров гидроаккустической системы в среде Mathcad. 4 3.Simulink-модель системы 9 4.Модельный эксперимент по оценке доплеровской частоты эхо-сигнала в заданной сигнально-помеховой ситуации 10 5. Определение смещенности оценки 14 6. Определение эффективности оценки 15 7. Определение состоятельности оценки 16 Вывод по 1 части 17 Часть 2. Исследование классификационной способности признаков при распознавании объектов 17 1.Исходные данные 17 2.Построение гистограмм распределения признаков x и y объектов w1 и w2 18 3.Построение плотности распределения вероятностей признаков x и y объектов w1 и w2 20 4.Построение диаграммы рассеяния признаков х и у объектов w1 и w2 25 6.Определение порогов классификации по каждому признаку 29 7.Определение частных вероятностей правильной классификации объекта 31 8.Определение наилучшего признака для классификации объекта 31 Вывод по 2 части 31 Список литературы 32 Приложение 1 33 Приложение 2 35 Часть 1. Флуктуационные ошибки оценки доплеровской частоты эхо-сигнала подводного объекта 3 2. Расчет параметров гидроаккустической системы в среде Mathcad. 4 3. Simulink-модель системы 7 4. Модельный эксперимент по оценке доплеровской частоты эхо-сигнала в заданной сигнально-помеховой ситуации 8 5. Определение смещенности оценки 10 6. Определение эффективности оценки 11 7. Определение состоятельности оценки 12 Вывод по 1 части 13 Часть 2. Исследование классификационной способности признаков при распознавании объектов 14 1. Исходные данные 14 2. Построение гистограмм распределения признаков x и y объектов w1 и w2 14 3. Построение плотности распределения вероятностей признаков x и y объектов w1 и w2 16 4. Построение диаграммы рассеяния признаков х и у объектов w1 и w2 21 6. Определение порогов классификации по каждому признаку 25 7. Определение частных вероятностей правильной классификации объекта 27 8. Определение наилучшего признака для классификации объекта 27 Вывод по 2 части 27 Список литературы 28 Приложение 1 28 Приложение 2 30 Часть 1. Флуктуационные ошибки оценки доплеровской частоты эхо-сигнала подводного объектаИсходные данные: 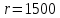 – максимальная дальность обнаружения объекта; – максимальная дальность обнаружения объекта; 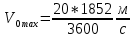 – максимальная скорость объекта; – максимальная скорость объекта;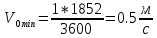 – минимальная скорость объекта; – минимальная скорость объекта;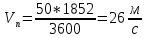 – скорость носителя ГАС; – скорость носителя ГАС;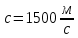 – средняя скорость звука в воде; – средняя скорость звука в воде;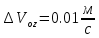 – аппаратная точность оценки скорости объекта; – аппаратная точность оценки скорости объекта;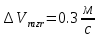 – разрешающая способность по скорости; – разрешающая способность по скорости;Мешающие помехи – ходовые (широкополосные) и ревербирационные; 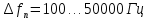 – частотная полоса широкополосных помех; – частотная полоса широкополосных помех;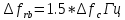 – частотная полоса ревербирационной помехи; – частотная полоса ревербирационной помехи;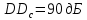 – динамический диапазон эхо-сигналов; – динамический диапазон эхо-сигналов;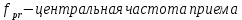 ; ;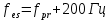 – частота эхо-сигнала при моделировании; – частота эхо-сигнала при моделировании;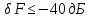 – уровни подавления боковых максимумов спектра сигнала; – уровни подавления боковых максимумов спектра сигнала;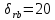 – минимальный уровень подавления реверберации; – минимальный уровень подавления реверберации;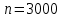 – количество опытов измерений; – количество опытов измерений;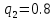 – заданное отношение сигнал/реверберационная помеха; – заданное отношение сигнал/реверберационная помеха;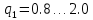 – заданное отношение сигнал/широкополосная c шагом 0.2; – заданное отношение сигнал/широкополосная c шагом 0.2;Расчет параметров гидроаккустической системы в среде Mathcad.Частота излучаемого сигнала: 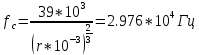 Разрешающая способность по частоте: 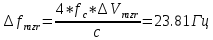 Примем разрешающую способность равной 20 Гц для дальнейших расчетов. Длительность излучаемого сигнала: 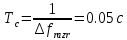 Частотная полоса излучаемого сигнала: 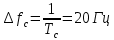 Цикл излучения: 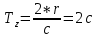 При моделировании ГАС примем цикл излучения равным 0.2 с, однако будем использовать синусоидальный непрерывный сигнал в целях уменьшения реального времени моделирования. Центральная частота приёма: 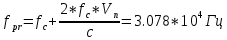 Частота эхо-сигнала при этом 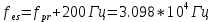 . .Частотная полоса реверберационной помехи: 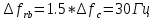 Доплеровская полоса: 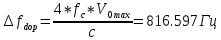 Частотная режекции режекторного фильтра: 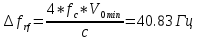 Частотная полоса приемного тракта: 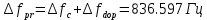 В Приложении 1 представлен фрагмент программы расчета в Mathcad. Частоту дискретизации выберем исходя из следующих условий: 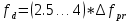 ; ;Ограниченность одной зоной Найквиста частотной полосы приема 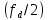 ; ;Частоту дискретизации примем равной 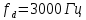 . .Уровень боковых лепестков спектра при использовании Окна Хэмминга значительно уменьшается, что в свою очередь увеличивает динамический диапазон спектрального анализа и ухудшает разрешающую способность в 1.36 раз. Для компенсации этого эффекта необходимо увеличить длительность излучаемого сигнала в 1.36 раз. Новая длительность сигнала: 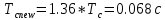 Длина линии задержки: 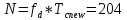 Требуемая точность оценки цифрового анализатора спектра: 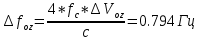 Примем требуемую точность оценки равной 0.75. Число точек БПФ: 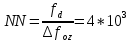 Число точек БПФ должно быть кратно степени 2, дополняем до 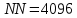 . .Тогда точность оценки, Гц 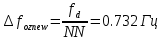  Рисунок 1 - Режекторный фильтр для борьбы с реверберационной помехой. Д 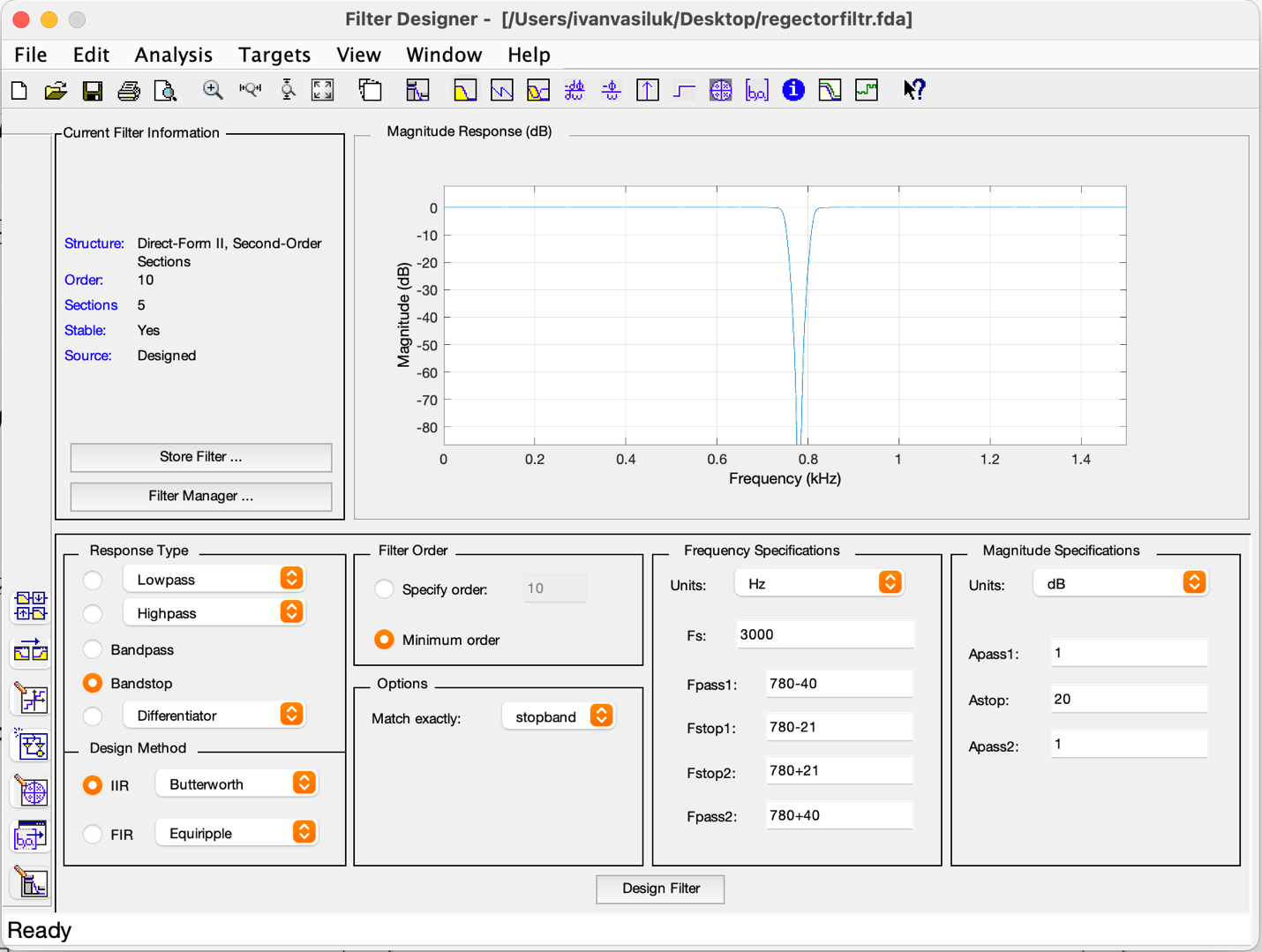 ля борьбы с реверберационной помехой построим режекторный фильтр. S |
| ОСП широкополосная q1 | Мат. ожидание |
| 0.8 | 980.6387 |
| 1.0 | 980.6631 |
| 1.2 | 980.6631 |
| 1.4 | 980.6631 |
| 1.6 | 980.6761 |
| 1.8 | 980.6729 |
| 2.0 | 980.6842 |
Все средние значения (мат. ожидания) оценок варьируются в пределах 99%, что означает менее 1% смещения, а значит все наши оценки в заданном интервале ОСП широкополосной – несмещенные.
6. Определение эффективности оценки
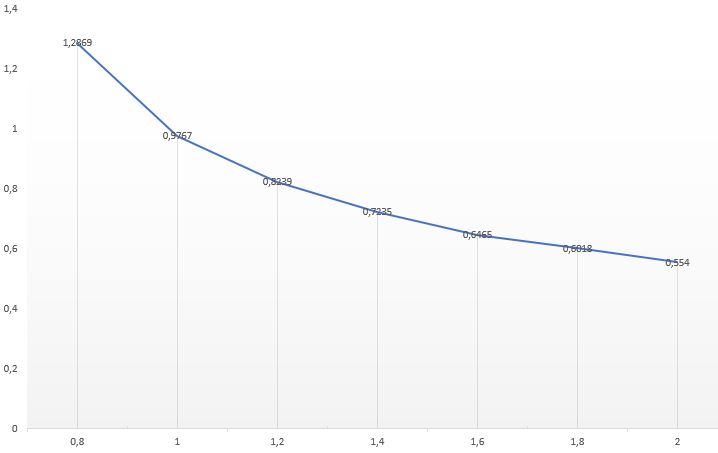
Эффективность оценки определяется величиной дисперсии несмещенных оценок. Так как все наши оценки несмещённые рассчитаем дисперсию (рассмотрим относительно СКО) для q1 от 0.8 до 2.0.
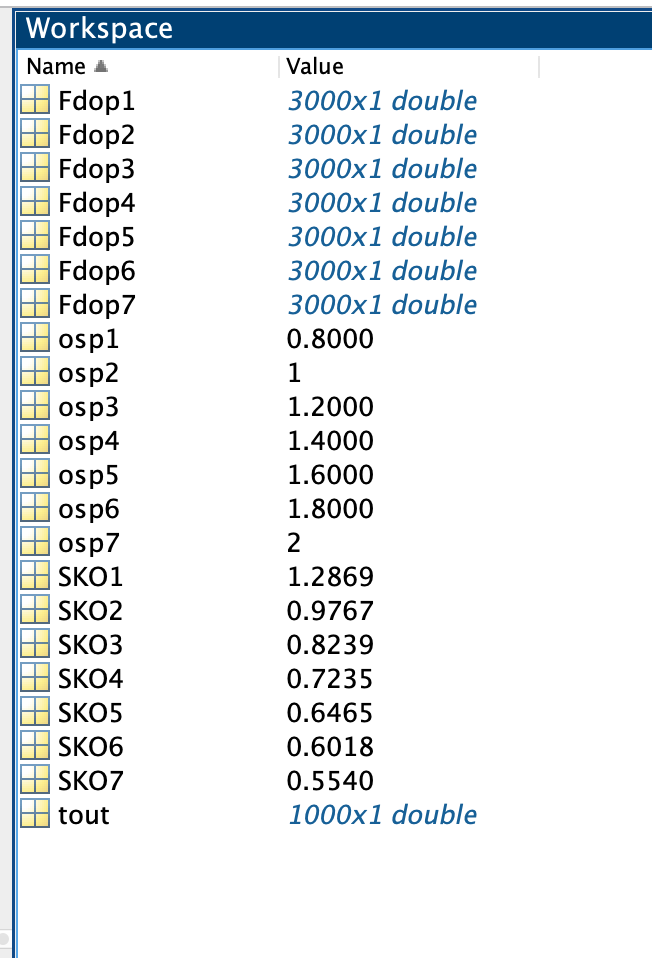
Таблица 2 – Оценка СКО для каждого q1
| ОСП широкополосная q1 | СКО |
| 0.8 | 1.2869 |
| 1.0 | 0.9767 |
| 1.2 | 0.8239 |
| 1.4 | 0.7235 |
| 1.6 | 0.6465 |
| 1.8 | 0.6018 |
| 2.0 | 0.5540 |
При q1=2.0 дисперсия наименьшая, а значит оценка fдоп наиболее эффективна при q1.
Расчет СКО ведется при помощи команды std в программе Matlab по общему количеству значений массива выходных оценок.
7. Определение состоятельности оценки
Т
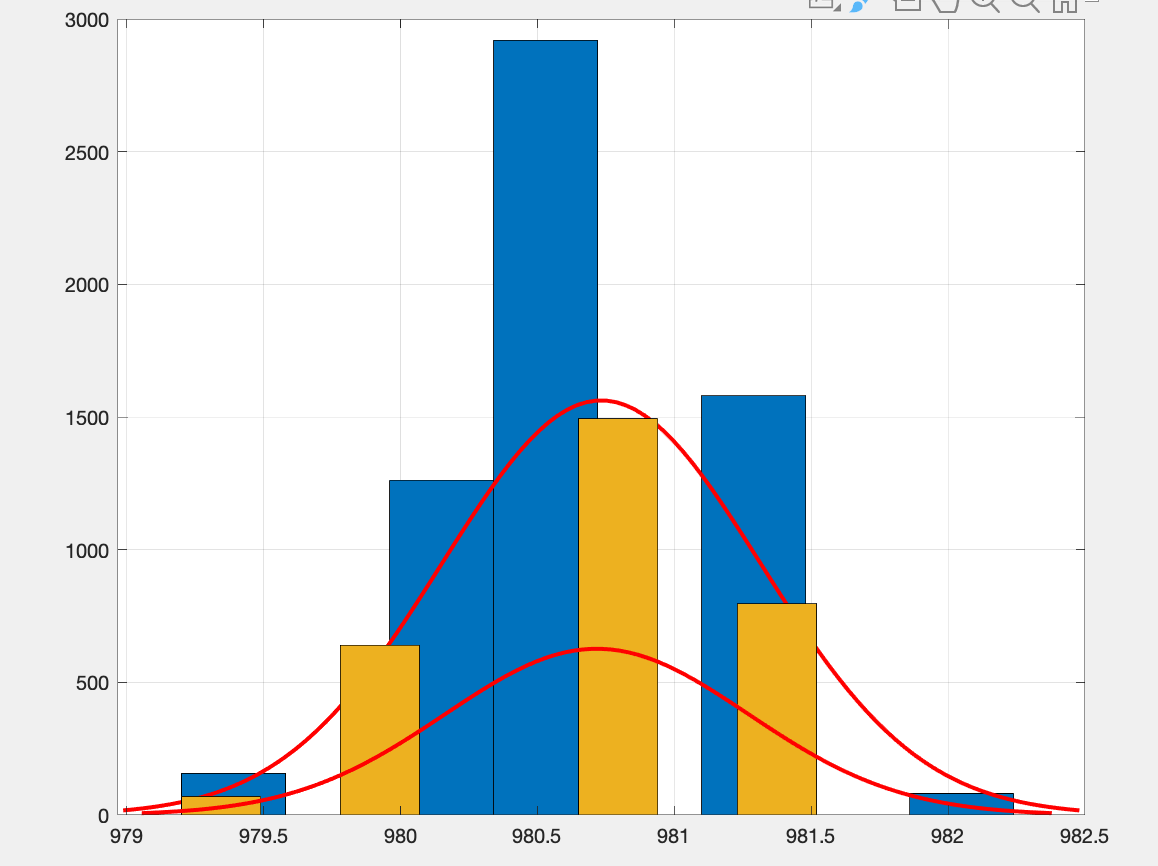
ак как при ОСП широкополосной равной 2.0 оценка наиболее эффективна, то будем оценивать состоятельность при данном значении. На рисунке 10 представлен график распределения оценок доплеровских частот для q1=2.0 при длине выборки 3000 и 6000, а также 1.1 и 2.2 модельных секунд. Для состоятельной оценки плотность вероятности оценки должна теснее концентрироваться относительно истинного значения параметра при увеличении количества отсчетов.
Рисунок 10 - Плотность распределения оценки для q1=2.0. (голубой 6000 отчётов, синий 3000)
Однако, на графике видно, что оценка является не состоятельной, так как отклоняется от истинного значения, а не концентрируется относительно него. При 3000 отсчетов СКО составляет 0.7321, а при 6000 – 0.7928.
Вывод по 1 части
Оценка
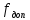 является несмещенной для всего интервала исследования, если брать погрешность в 10%.
является несмещенной для всего интервала исследования, если брать погрешность в 10%.Оценка
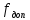 наиболее эффективна при q1=2.0.
наиболее эффективна при q1=2.0.Оценка
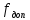 является не состоятельной
является не состоятельной Все оценки являются несмещенными, при этом самой эффективной является при q1=2.0, q2=0.8. Однако при увеличении выборки происходит отклонение от истинного значения, что говорит о не состоятельности оценки.
Часть 2. Исследование классификационной способности признаков при распознавании объектов
Исходные данные
Объекты классификации: w1 и w2;
Классификационные признаки: x и y;
Длина выборки каждого признака: N=100;
Выборочные значения признаков x и y объектов w1 и w2 в виде mat-файлов данных;
Вероятность ложной классификации – 0.05.
Построение гистограмм распределения признаков x и y объектов w1 и w2

Рисунок 11 - Гистограмма распределения признака х1 объекта w1.
Г
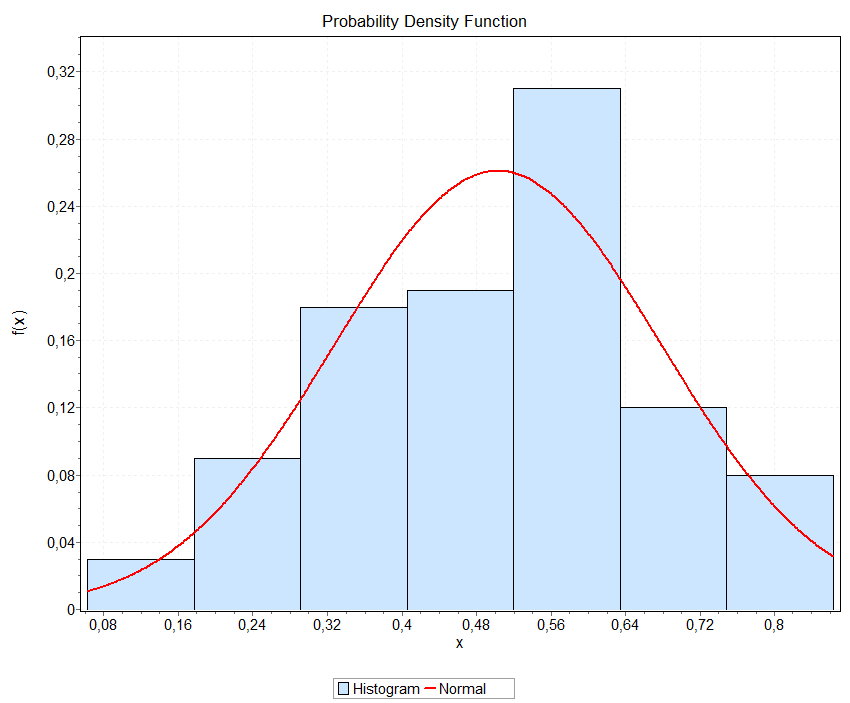
истограммы распределений классификационных признаков x1, x2, y1 и y2 были получены с помощью программы EasyFit 5.5

Рисунок 12 - Гистограмма распределения признака x2 объекта w2.
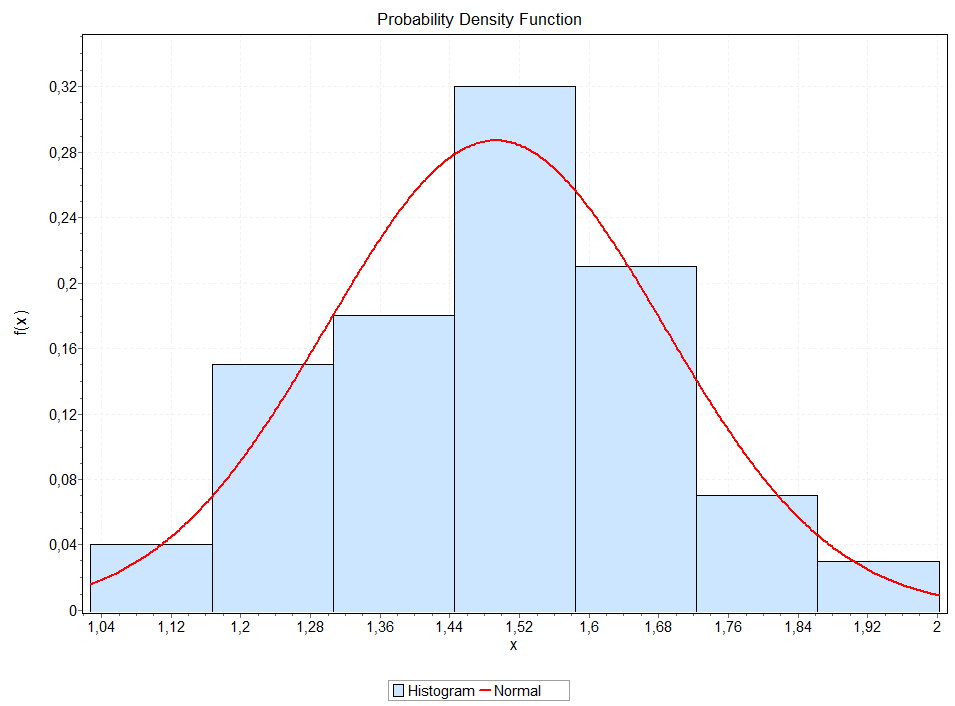
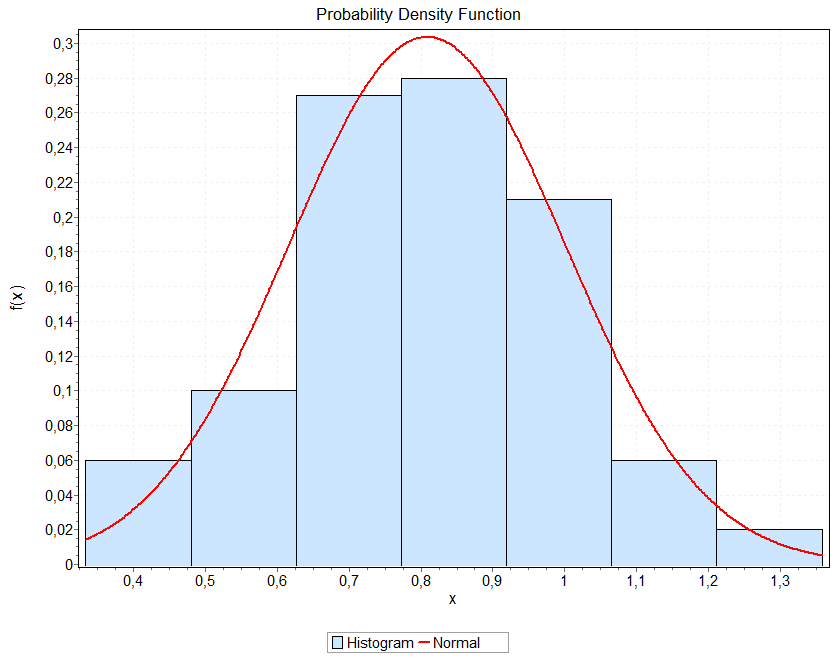

Рисунок 13 - Гистограмма распределения признака y1 объекта w1.

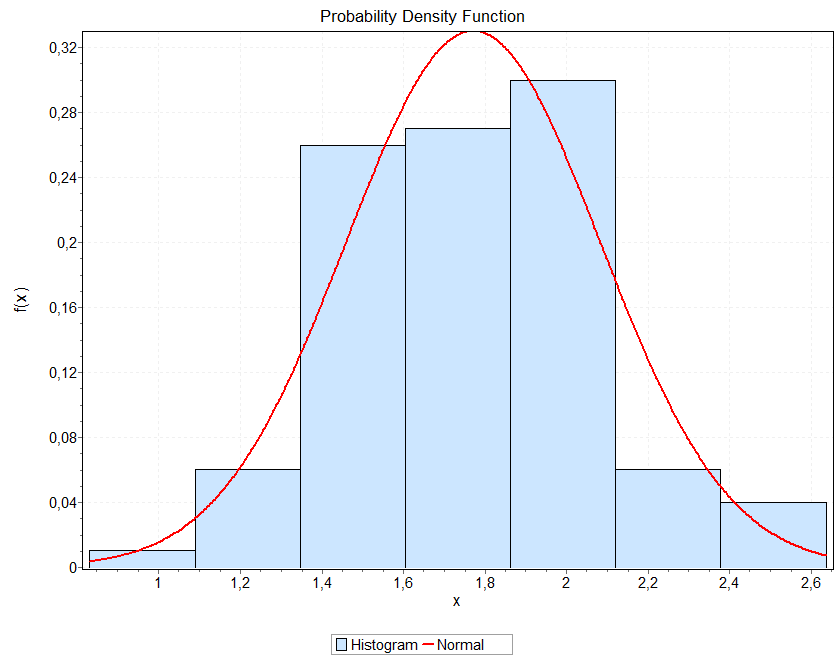
Рисунок 14 - Гистограмма распределения признака y2 объекта w2.
Построение плотности распределения вероятностей признаков x и y объектов w1 и w2
Графики плотностей распределения вероятностей классификационных признаков x1, x2, y1 и y2 были получены с помощью программы Matlab.

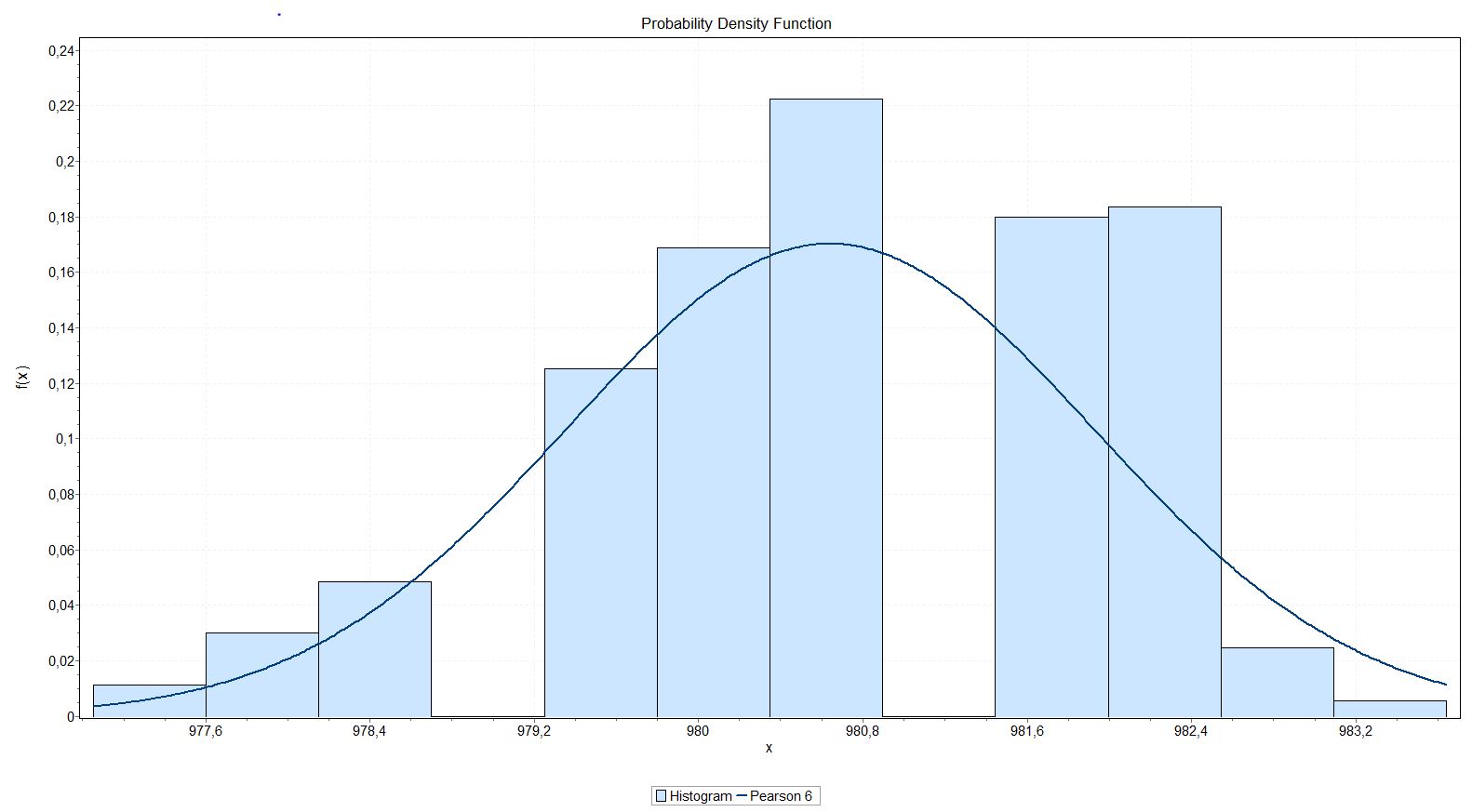
Рисунок 15 - График плотностей распределения вероятностей классификационных признаков x1, x2.
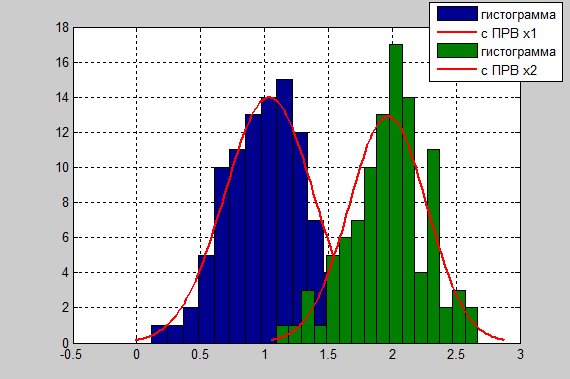

Рисунок 16 - График плотностей распределения вероятностей классификационных признаков y1, y2.
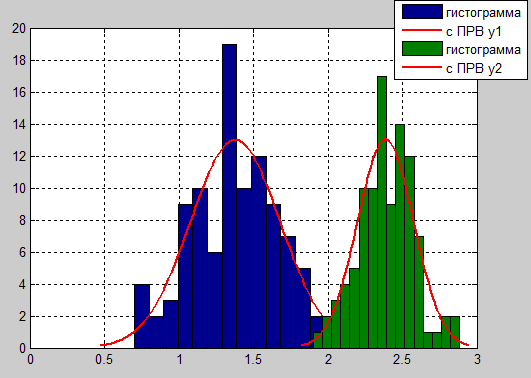
Определение законов распределения
Уровень значимости для данного раздела принимаем равным 0.05
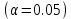 и точечные оценки распределения (m и σ) признаков х и у объектов w1 и w2.
и точечные оценки распределения (m и σ) признаков х и у объектов w1 и w2.Для выявления законов распределений классификационных признаков объектов воспользуемся критерием Колмогорова-Смирнова, поскольку он чувствителен не только к различию в положении двух распределений, например, к различиям средних, но также чувствителен и к форме распределения. Кроме того, критерий Колмогорова-Смирнова рекомендуют применять при малых объемах выборки
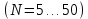 , и в случае сравнения эмпирической и теоретической функций распределения.
, и в случае сравнения эмпирической и теоретической функций распределения.В соответствии с критерием Колмогорова-Смирнова находится максимальная по модулю разность между выборочной (опытной) функцией распределения
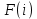 и теоретической
и теоретической 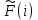 :
: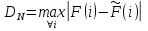
Величина
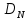 , рассчитанная по данным выборки, сравнивается с критическим значением
, рассчитанная по данным выборки, сравнивается с критическим значением 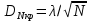 , где
, где 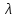 - значения статистики Колмогорова-Смирнова (эти значения табулированы), соответствующие заданному уровню значимости
- значения статистики Колмогорова-Смирнова (эти значения табулированы), соответствующие заданному уровню значимости 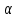 (т.е. вероятности отклонения проверяемой гипотезы, принято
(т.е. вероятности отклонения проверяемой гипотезы, принято 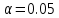 ), а
), а 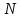 - размер выборки.
- размер выборки. Если
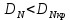 , то принимается гипотеза о соответствии закона распределения исследуемой выборки теоретическому закону распределения.
, то принимается гипотеза о соответствии закона распределения исследуемой выборки теоретическому закону распределения. Результаты оценки законов распределений классификационных признаков x1, x2, y1 и y2 были получены с помощью программы EasyFit 5.5 и приведены на рисунках 18, 20, 21, 22.
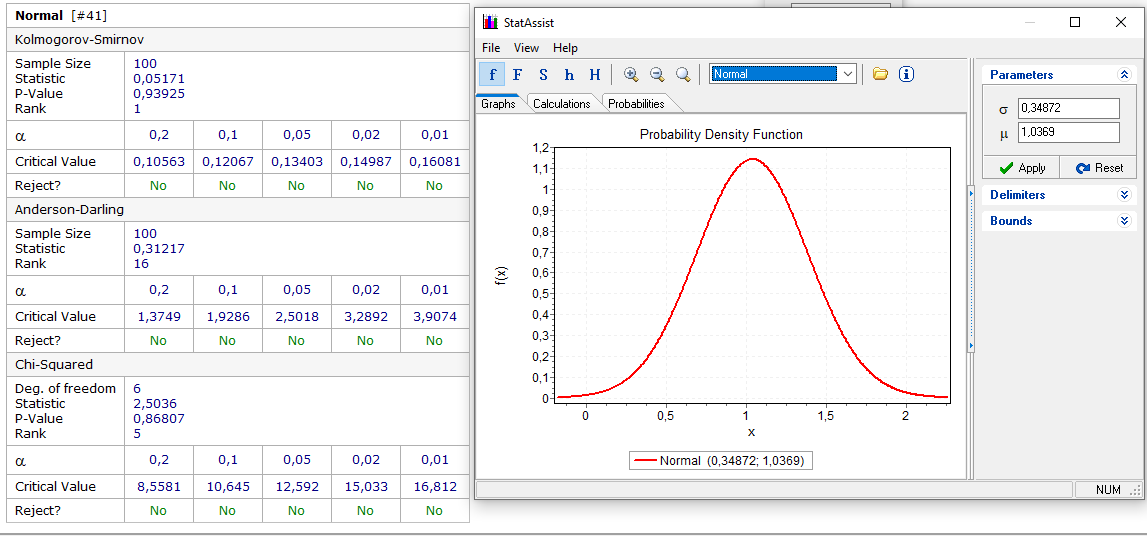
Рисунок 17 - Определение закона распределения признака х1.
По критерию согласия Колмогорова-Смирнова с уровнем значимости
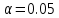 гипотеза о нормальности распределения случайной величины x1 не отбрасывается.
гипотеза о нормальности распределения случайной величины x1 не отбрасывается.Точечные оценки (мат. ожидание и СКО) определим также с помощью программы EasyFit в разделе Calculations:
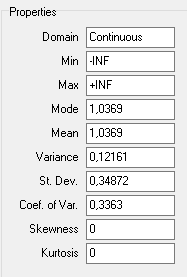
Рисунок 18 - Расчёт мат.ожидания (mean) и дисперсии (St. Dev.)
Мат. ожидание для признака х1:
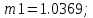
СКО для признака x1:
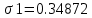 .
.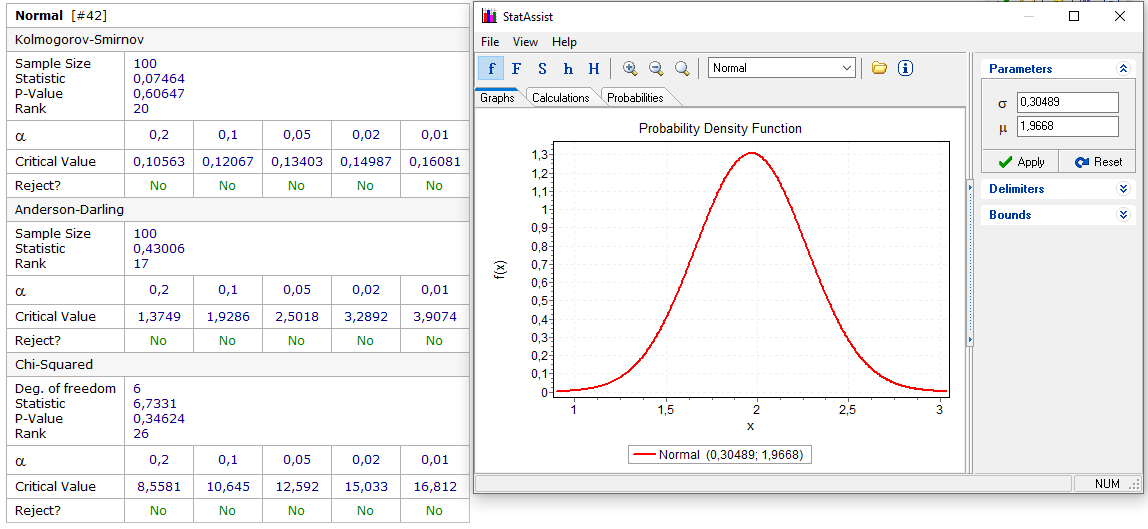
Рисунок 19 - Определение закона распределения признака х2.
По критерию согласия Колмогорова-Смирнова с уровнем значимости
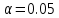 гипотеза о нормальности распределения случайной величины x2 не отбрасывается.
гипотеза о нормальности распределения случайной величины x2 не отбрасывается.Мат. ожидание для признака х2:
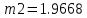 ;
;СКО для признака x2:
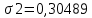 ;
;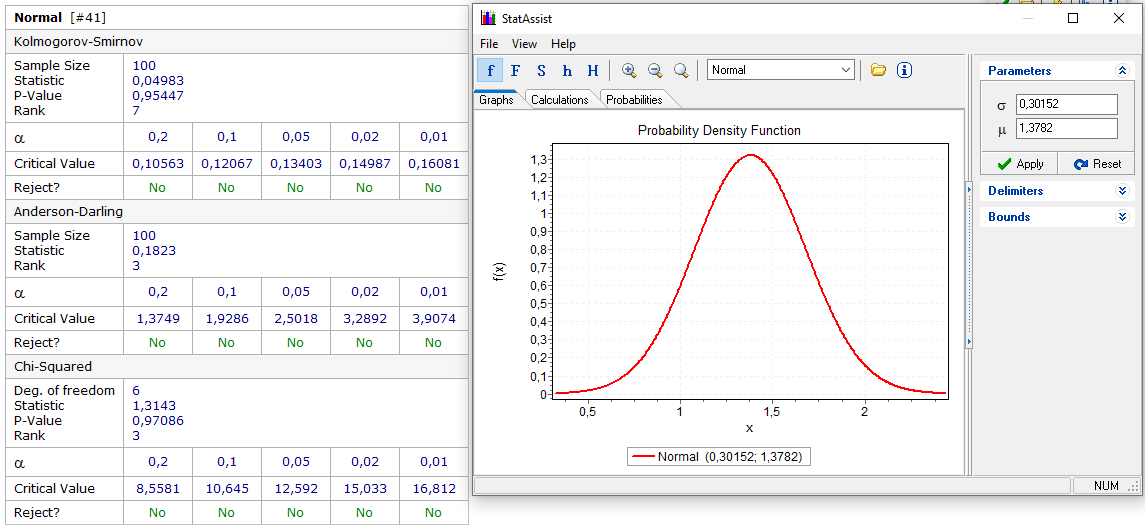
Рисунок 20 - Определение закона распределения признака y1.
По критерию согласия Колмогорова-Смирнова с уровнем значимости
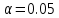 гипотеза о нормальности распределения случайной величины у1 не отбрасывается.
гипотеза о нормальности распределения случайной величины у1 не отбрасывается.Мат. ожидание для признака y1:
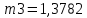 ;
;СКО для признака y1
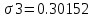 ;
;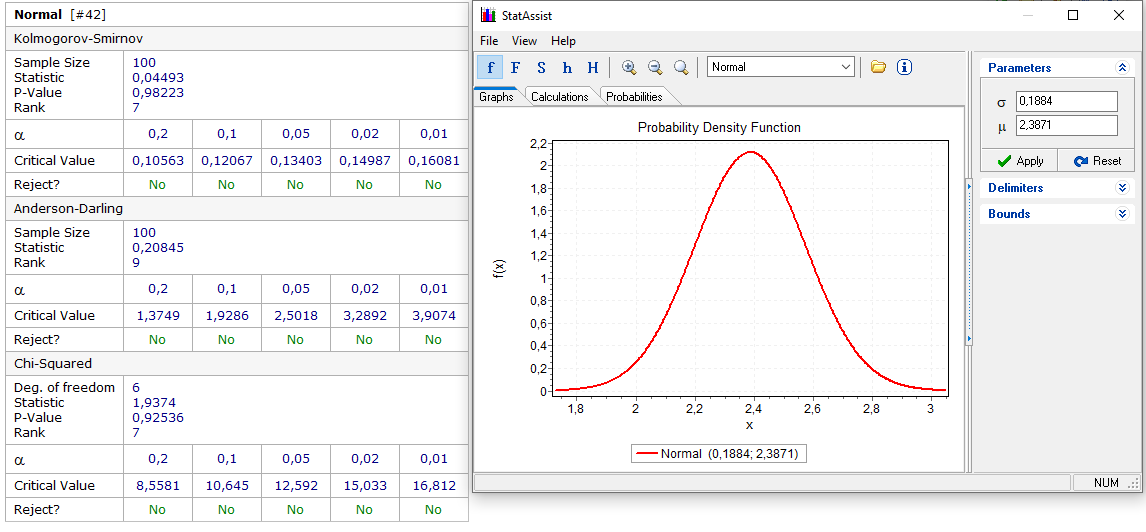
Рисунок 21 - Определение закона распределения признака y2.
По критерию согласия Колмогорова-Смирнова с уровнем значимости
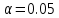 гипотеза о нормальности распределения случайной величины у2 не отбрасывается.
гипотеза о нормальности распределения случайной величины у2 не отбрасывается. Мат. ожидание для признака y2 m4 =2.3871;
СКО для признака y2 σ4=0.1884.
Построение диаграммы рассеяния признаков х и у объектов w1 и w2
Классификационные признаки могут быть использованы в целях распознавания объекта лишь при условии, если они удовлетворяют определенным критериям.
Признаки должны быть независимыми и информативными (значимыми!).
Свойства объекта (классификационные признаки) могут быть зависимыми друг от друга, и степень этой зависимости бывает различной. В некоторых случаях появление одного признака неизбежно вызывает появление другого. Если обнаруживается взаимная зависимость некоторых признаков, то в выявленную совокупность признаков для классификации целей такие признаки не включаются как не имеющие самостоятельного идентификационного значения. Если парные коэффициенты взаимной корреляции небольшие (взаимная зависимость признаков мала), то в выявленную совокупность включатся все признаки.
Для оценки парной корреляции между нормально распределенными классификационными признаками
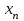 и
и 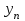 используется классический коэффициент корреляции Пирсона:
используется классический коэффициент корреляции Пирсона: 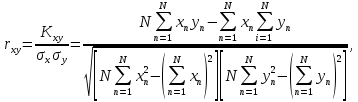
где
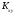 – ковариация признаков;
– ковариация признаков; 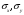 – СКВО оценок признаков
– СКВО оценок признаков  и
и 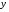
Будем считать, что x1 и y1 – два признака одного объекта;
| x1y1=[x1, y1]; x2y2=[x2, y2]; R=corrcoef(x1y1); R=corrcoef(x2y2); | - объединение массивов в матрицу 2х100 - оценка коэффициента корреляции |
При анализе зависимостей между парами признаком используется следующая интерпретация значений коэффициента корреляции:
Таблица 3 – Значения корреляции
| Коэфф. корр. | Интерпретация |
| 0…0.19 | очень слабая корреляция |
| 0.2…0.49 | слабая корреляция |
| 0.5…0.69 | средняя корреляция |
| 0.7…0.89 | сильная корреляция |
| 0.9…1 | очень сильная корреляция |
Коэффициент корреляции между признаками x1 и y1:
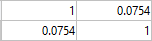
Где, 1 – коэффициент автокорреляции каждого признака, 0.0754 – коэффициент парной корреляции двух признаков. Используя таблицу интерпретаций значений коэффициента, устанавливаем, что между признаками x1 и y1 – очень слабая корреляция.
Коэффициент корреляции между признаками x2 и y2:

Между признаками x2 и у2 – очень слабая корреляция.
З
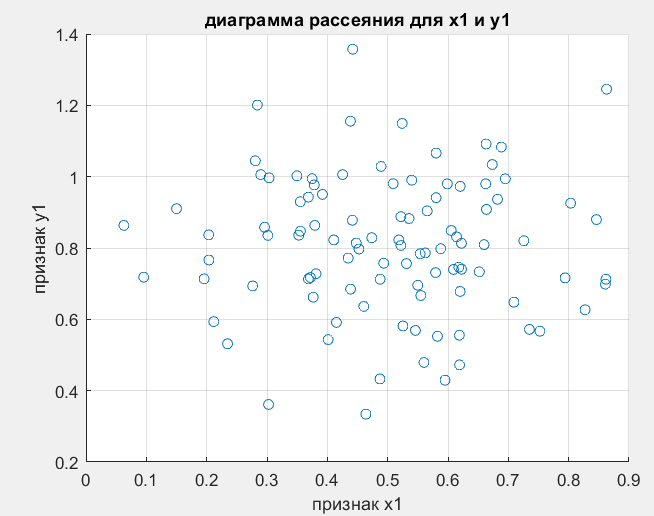
рительно проверить гипотезу о наличии или отсутствии определенной парной взаимосвязи между классификационными признаками можно с помощью диаграмм рассеяния. Чем теснее группируются выборки признаков вокруг воображаемой кривой зависимости величин, тем строже эта зависимость между признаками. На рисунках 23 и 24 представлены диаграммы рассеяния признаков.
Рисунок 22 - Диаграмма рассеяния для х1 и у1
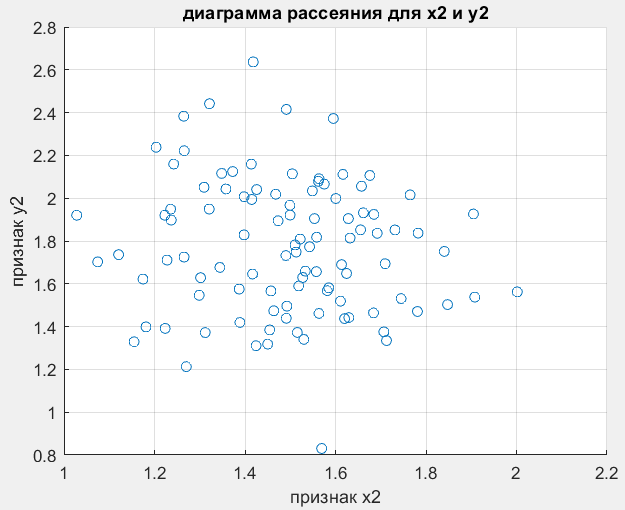
Рисунок 23 - Диаграмма рассеяния для х2 и у2.
Диаграммы рассеяния подтверждают очень слабую корреляцию между этими признаками, так как точки не сгруппированы, а сильно разбросаны.
Определение информативности признаков х и у объектов w1 и w2
С точки зрения минимизации затрат для оценки значимости классификационных признаков наиболее удобными являются информационные меры, показывающие не абсолютное значение риска потерь, а сравнительную ценность признаков. Смысл информационных мер состоит в количественной оценке «разнесённости» распределений значений признаков различных классов целей
Наиболее удобной мерой является Махаланобисово расстояние, представляющее собой дистанционную меру, которая базируется на евклидовых расстояниях между нормализованными значениями оценок классификационных признаков двух классов объектов, с учетом корреляции соответствующих переменных. Мера Махаланобиса вычисляется по формуле
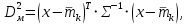
где
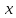 - оценки классификационного признака исследуемого класса цели,
- оценки классификационного признака исследуемого класса цели, 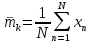 - выборочное среднее оценок признака
- выборочное среднее оценок признака 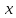 для эталонного класса
для эталонного класса 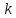 ,
, 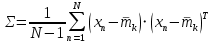 - ковариационная матрица,
- ковариационная матрица, 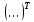 - знак транспонирования.
- знак транспонирования. 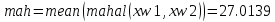 - расчет расстояния Махаланобиса в Matlab для признаков x1 и x2.
- расчет расстояния Махаланобиса в Matlab для признаков x1 и x2.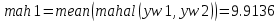 - расчет расстояния Махаланобиса в Matlab для признаков y1 и y2.
- расчет расстояния Махаланобиса в Matlab для признаков y1 и y2.Признаки x1 и x2 являются более информативными, так как они больше разнесены, что показывает Махаланобисово расстрояние.
Определение порогов классификации по каждому признаку
Необходимо подобрать порог для эффективного обнаружения объекта w1. Изображение двух плотностей распределения признаков с выставленным порогом представлено на рисунке 24.
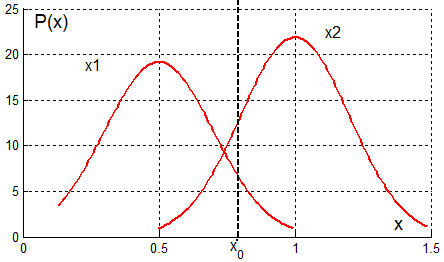
Рисунок 24 - Визуализация двух плотностей распределения признаков, где x0 - пороговое значение, x1 и x2 – два признака одного объекта.
При выборе порога классификации будем исходить из условия, что вероятность ложной тревоги не должна превышать 5%, нахождение производится посредством Matlab:
% Расчет вероятности правильной классификации
% поиск порога x0, ВЛК = 0.05
x0 = 1.41; % порог
px1 = find(xw1 <= x0); %поиск значений xw1
px2 = find(xw2 < x0); %поиск значений xw2
N1 = size(px1, 1); %определение числа значений xw1
N2 = size(px2, 1); %определение числа значений xw2
VLK1 = N2/N %определение ВЛК по xw2
VPK1 = N1/N %определение ВПК по xw1
% поиск порога y0, ВЛК = 0.05
y0 = 2.0; % порог
py1 = find(yw1 <= y0); %поиск значений yw1
py2 = find(yw2 < y0); %поиск значений yw2
N11 = size(py1, 1); %число значений yw1
N22 = size(py2, 1); %число значений yw2
VLK2 = N22/N %определение ВЛК по yw2
VPK2 = N11/N %определение ВПК по yw1
Пороговый коэффициент для признаков х равен 1.8, при этом вероятность правильной классификации 0.95
Пороговый коэффициент для признаков y равен 1.12, при этом вероятность правильной классификации 0.8.
Определение частных вероятностей правильной классификации объекта
Вероятность правильной классификации для признаков х равна 0.95.
Вероятность правильной классификации для признаков у равна 0.8.
Определение наилучшего признака для классификации объекта
Вероятность правильной классификации для признаков x выше, они информативнее, значит наилучшими признаками для классификации объекта являются признаки у.
Вывод по 2 части
В данной части курсовой работы были построены гистограммы и плотности для признаков (х) и (у) объектов (w1) и (w2), определены законы распределения.
Выяснено, что плотности распределения для каждого признака подчиняются нормальному закону по критерию Колмогорова-Смирнова.
Определено, что признаки (x) являются более информативными.
ВПК по признакам x выше.
Признаки (x) являются наилучшими для классификации объекта.
Все расчёты и построения приведены в приложении 2.
Список литературы
Свердлин Г.М. Гидроакустические преобразователи и антенны 1988.
Конспекты лекций по дисциплине «Преобразователи и антенны перспективных ГАС»
Исаков В.Н. Статистическая теория радиотехнических систем.
Сейдж Э.П., Мелс Дж. теория оценивания и ее применение в связи и управлении. – М.: Связь, 1976
Сосулин Ю.Г. теория обнаружения и оценивания стохастических сигналов М.: Сов.Радио, 1978 г.
Richard O. Duda, Peter E. Hart, David G. Stork. Pattern Classification (Second Editor). A Wiley-Interscience Publication, 2001.–p.654
Приложение 1


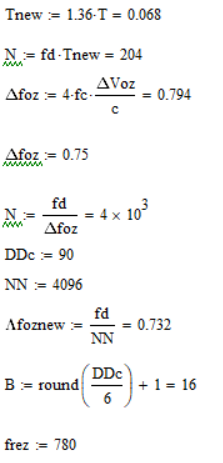
Приложение 2
close all;
% по массивам выборок для параметров xw1 xw2 yw1 yw2
x1=xw1;
x2=xw2;
y1=yw1;
y2=yw2;
m1 = mean(x1); % МО признака x1
sigma1 = std(x2); % СКО признака x1
m3 = mean(y1); % МО признака y1
sigma3 = std(y1); % СКО признака y1
m2 = mean(x2); % МО признака x2
sigma2 = std(x2); % СКО признака x2
m4 = mean(y2); % МО признака y2
sigma4 = std(y2); % СКО признака y2
N = 100; % размерность признаков
7
figure
plot(x1, '-b')
grid on
hold on
plot(x2, '-r')
grid on
legend('признак x1','признак x2')
figure
plot(y1, '-b')
grid on
hold on
plot(y2, '-r')
grid on
legend('признак y1','признак y2')
% гистограмма распределения
k = round(1+3.322*log(N)); % количество интервалов распределения
figure;
grid on
hold on
histfit(x2, k); %гистограмма и ПРВ
histfit(x1, k);
legend('гистограмма и ПРВ x2','','гистограмма и ПРВ x1','');
figure;
grid on
hold on
histfit(y2, k); %гистограмма и ПРВ
histfit(y1, k);
legend('гистограмма и ПРВ y2','','гистограмма и ПРВ y1','');
% корреляция
x1y2=[x1,y1];
x2y2=[x2,y2];
R=corrcoef(x1,y1); %коэффициент парной корреляции); %1 - автокорреляция, 0.1.. - между собой
% нормальное распределение - корреляция практически отсутствует
R1=corrcoef(x2,y2);
% диаграмма рассеяния
figure;
scatter(x1,y1); %построение диаграмм рассеяния
grid on;
title('диаграмма рассеяния для x1 и y1')
xlabel('признак x1');
ylabel('признак y1');
figure;
scatter(x2,y2); %построение диаграмм рассеяния
grid on;
title('диаграмма рассеяния для x2 и y2')
xlabel('признак x2');
ylabel('признак y2');
%информативность признака
%мера Махаланобиса
mah=mean(mahal(x1,x2));
mah1=mean(mahal(y1,y2));
%расчет вероятности правильной классификации
%поиск порога х0, вероятность ложной классификации 0.1
x0=0.95;
a=find(x2>x0);
N1=size(a);
VLK=N1(1,1)/N %вероятность ложной классификации для x
%расчет ВПК
b=find(x1>=x0);
N2=size(b);
VPK=N2(1,1)/N %вероятность правильной классификации для x
y0=2.0;
a1=find(y2>y0);
N3=size(a1);
VLK1=N3(1,1)/N %вероятность ложной классификации для у
% расчет ВПК
b1=find(y1>=y0);
N4=size(b1);
VPK1=N4(1,1)/N %вероятность правильной классификации для у