9305_АникинаАА. Курсовая работа по дисциплине архитектура эвм вариант 3 студентка группы 9305 Аникина Анна Проверил
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
2.2.3. Выбор форматов данных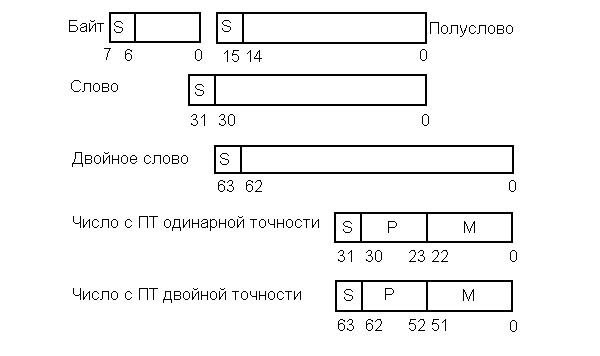 Рис. 1. Основные используемые типы данных Проектируемый процессор поддерживает знаковые и беззнаковые целые числа, числа с плавающей точкой различной разрядности. Целые числа Целые числа могут занимать байт, слово или двойное слово. Они могут быть знаковыми и беззнаковыми. В знаковых целых самый старший бит байта, слова или двойного слова, занимаемого числом, отводится для индикации знака числа. Нуль соответствует плюсу, 1 — минусу. Таким образом, возможный диапазон представляемых значений для знаковых целых составляет: от –128 до 127 для байта, от –231 до 231 для слов, от –263 до 263 для двойных слов. Беззнаковые целые могут принимать значения: от 0 до 255 для байт, от 0 до 232-1 для слов, от 0 до 264-1 для двойных слов. Числа с плавающей точкой Числа можно представить в виде: 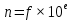 , где , где 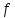 – мантисса, а – мантисса, а 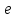 – экспонента (положительное или отрицательное целое число). Такое представление чисел в компьютере называется представление числа с плавающей точкой. – экспонента (положительное или отрицательное целое число). Такое представление чисел в компьютере называется представление числа с плавающей точкой. Область значений определяется по числу разрядов в экспоненте, а точность – по числу разрядов в мантиссе. Числа с плавающей точкой могут быть 32-разрядные (одинарной точности) и 64-разрядные (двойной точности). Оба формата представления чисел с плавающей точкой начинаются со знакового бита: 0 соответствует положительному числу, 1 – отрицательному. Затем следует смещенная экспонента. Для формата одинарной точности смещение равно 127, а для формата двойной точности – 1023. Минимальная (0) и максимальная (255 и 2047) экспоненты не используются для нормализованных чисел. Область значений экспоненты для формата одинарной точности : от -126 до 127, для формата двойной точности: от -1022 до 1023. Нормализованная мантисса начинается с двойной точки, за которой следует 1 бит, а затем – остаток мантиссы. Мантисса состоит из неявного бита, который всегда равен 1, и неявной двойной точки, за которыми идут 23 или 52 произвольных бита. Если все 23 или 52 бита мантиссы равны 0, то мантисса имеет значение 1,0. Иначе, если все биты равны 1, то числовое значение мантиссы немного меньше, чем 2,0. Существуют проблемы, связанные с числами с плавающей точкой: потеря значимости переполнение неинициализированные числа Поэтому помимо нормализованных чисел предусмотрено еще 4 типа чисел.  Рис. 2. Числовые типы Потеря значимости: Для решения данной проблемы были введены ненормализованные числа. Они имеют экспоненту 0 и мантиссу, представленную следующими 23 или 52 битами. Неявный 1 бит слева от двоичной точки превращается в 0. Ненормализованные числа отличаются от нормализованных тем, что у последних не может быть нулевой экспоненты. Самое маленькое нормализованное число с одинарной точностью содержит 1 в экспоненте и 0 в мантиссе и представляет 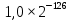 . . Самое большое ненормализованное число содержит 0 в экспоненте и все единицы в мантиссе и представляет примерно 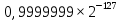 . (Оно почти равно cамому маленькому нормализованному числу). Это число содержит 23 бита значимости, а все нормализованные числа с одинарной точностью – 24 бита. . (Оно почти равно cамому маленькому нормализованному числу). Это число содержит 23 бита значимости, а все нормализованные числа с одинарной точностью – 24 бита.Самое маленькое ненулевое ненормализованное число с одинарной точностью содержит 1 в крайнем правом бите, а все остальные равны 0. Значение таким образом равно 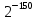 ( ( 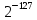 -экспонента, -экспонента, 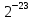 – мантисса). Таким образом, идет постепенное исчезновение значимых разрядов. – мантисса). Таким образом, идет постепенное исчезновение значимых разрядов. В такой схеме присутствует два нуля, положительный и отрицательный (имеют мантиссу и экспоненту = 0, различие по знаковому биту). Переполнение: Для решения этой проблемы существует специальное представление бесконечности: с экспонентой, содержащей все 1, и мантиссой, равной 0. Это число подчиняется обычным математическим правилам для бесконечности. Для не определенного результата (например, бесконечность делить на бесконечность) существует специальный формат – не число (NaN). У такого формата экспонента содержит одни 1, а мантисса – любой ненулевой набор битов. |
