Курсовая работа по дисциплине Цифровые системы управления в мехатронике АлФахри Ф. Ф. А. М
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
5.2. Синтез регулятора положения в системе с астатизмом первого порядкаОпределяем параметры желаемой передаточной функции ЭП. Коэффициент передачи по скорости: 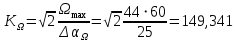 с– 1. с– 1.Коэффициент передачи по ускорению: 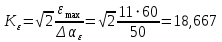 с– 2. с– 2.Значение базовой частоты будет равно: 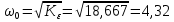 с– 1. с– 1.Рассчитываем постоянные времени: 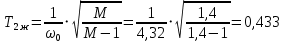 с; с;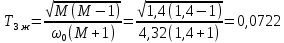 с. с.Рассчитываем протяжённость среднечастотного участка желаемой ЛАЧХ:  . .Частоту, соответствующую максимальному запасу по фазе определяем по формуле: 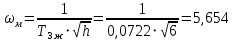 с– 1. с– 1.По условию обеспечения максимального запаса по фазе находим постоянную времени 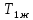 : :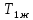 1/ 1/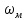 = 1/5,654 = 0,176 с. = 1/5,654 = 0,176 с.Принимаем 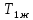 = 2 с. = 2 с.С учётом проведённых расчётов желаемая передаточная функция ЭП с астатизмом первого порядка запишется как: 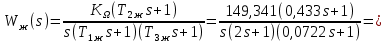  Составляем программу для определения передаточной функции регулятора положения ЭП с астатизмом первого порядка. Передаточную функцию неизменяемой части принимаем по примеру 5.1. num1=[64.66 149.341]; den1=[0.1444 2.0722 1 0]; sys1=tf(num1,den1); num2=[0.001981 0.5151 37.86 616.2]; den2=[9.405e-11 1.681e-07 6.828e-05 0.01025 0.6805 23.37 281.4 0]; sys2=tf(num2,den2); sys3=sys1/sys2 sys3 = 6.081e-09 s^8 + 1.088e-05 s^7 + 0.00444 s^6 + 0.673 s^5 + 45.53 s^4 + 1613 s^3 + 2.169e04 s^2 + 4.202e04 s ------------------------------------------------------------------ 0.0002861 s^6 + 0.07849 s^5 + 6.536 s^4 + 167.9 s^3 + 1315 s^2 + 616.2 s Составляем программу для определения ЛАЧХ регулятора положения, изображенную на рис. 5.2.1: num=[ 6.081e-09 1.088e-05 0.00444 0.673 45.53 1613 2.169e04 4.202e04 0]; den=[0.0002861 0.07849 6.536 167.9 1315 616.2 0]; bode(num,den) Переходим к анализу полученных графиков. Низкочастотный участок ЛАЧХ РП проходит параллельно оси частот, постепенно изменяя наклон к среднечастотному участку в пределах от 0 до –20 дБ/дек и далее к 0 дБ/дек. Высокочастотный участок ЛАЧХ с увеличением частоты изменяет свой наклон также в пределах от 20 до 40 дБ/дек. Полученные ЛАЧХ следует аппроксимировать пятью асимптотами и придать регулятору положения свойства интегро-дифференцирующего регулятора.  Рис. 5.2.1. ЛАЧХ регулятора положения Рассчитаем параметры передаточной функции. Находим коэффициент передачи Крп. Из графика рис. 5.2.1 имеем:  дБ, дБ,откуда 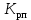 = 68,4. Частоты сопряжения 1 = 0,406 с– 1; 2 = 5,07 с– 1; 3 = 158 с– 1; 4 = 1000 с– 1 и постоянные времени: = 68,4. Частоты сопряжения 1 = 0,406 с– 1; 2 = 5,07 с– 1; 3 = 158 с– 1; 4 = 1000 с– 1 и постоянные времени: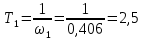 с; с;  с; с;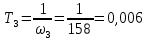 с; с; 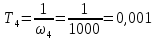 с. с.С учётом полученных значений передаточная функция синтезированного регулятора положения принимает вид: 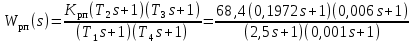 . .Переходим к построению и моделированию ССДМ ЭП, показанной на рис. 5.2.2. Для формирования линейно возрастающих воздействий 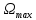 и и 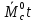 используются блоки Ramp и Ramp1. используются блоки Ramp и Ramp1.
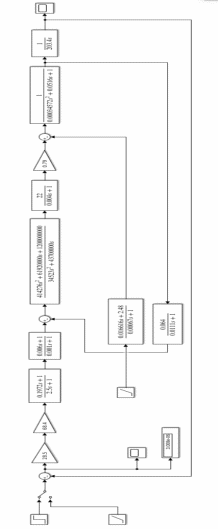 Результаты моделирования показаны на рис. 5.2.3 – 5.2.5. α(t), рад 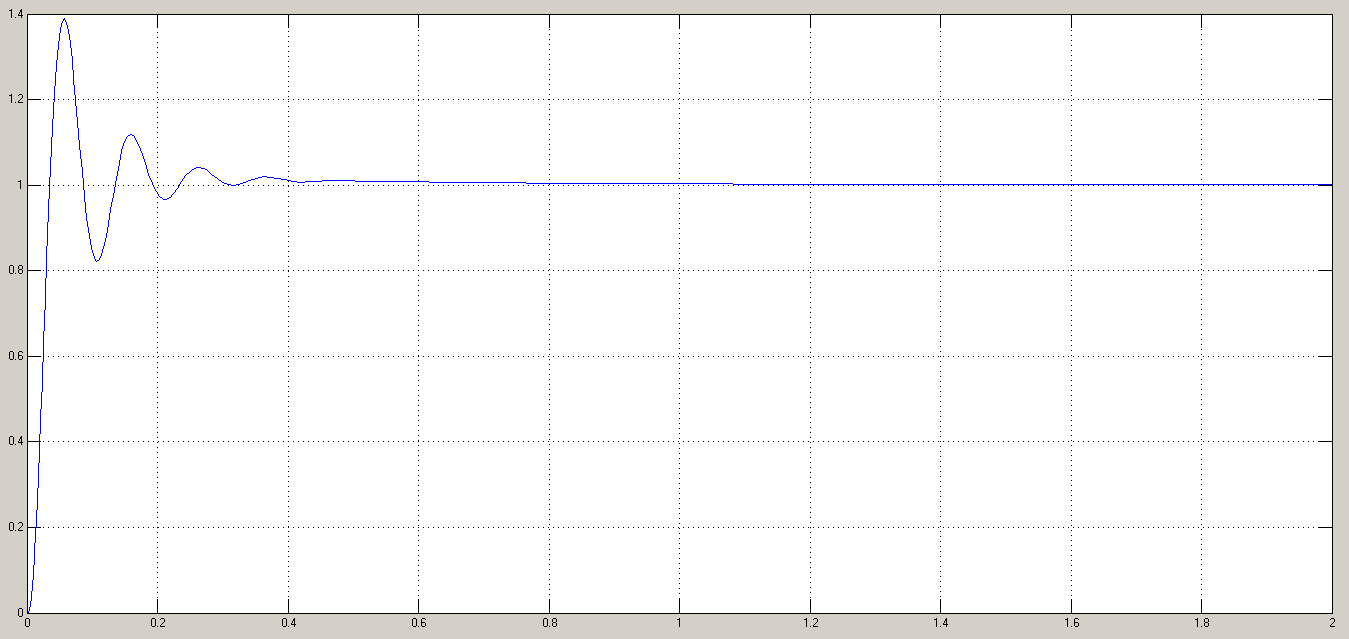 t, c t, cРис. 5.2.3. Переходная характеристика системы по задающему воздействию 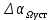 , рад , рад t, c t, cРис. 5.2.4. График ошибки системы при линейно возрастающем задающем воздействии 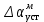 , рад , рад t, c t, cРис. 5.2.5. График моментной составляющей ошибки системы при линейно возрастающем моменте сопротивления Анализ графика (рис. 5.2.3) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие 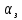 примерно за 1 с, с перерегулированием примерно за 1 с, с перерегулированием 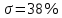 и числом колебаний N = 3, что соответствует заданному показателю колебательности. и числом колебаний N = 3, что соответствует заданному показателю колебательности.Поскольку система включает интегрирующее звено на выходе, то очевидно, что статическая ошибка будет равна нулю. На рис. 5.2.4 представлена характеристика ЭП при линейно возрастающем задающем воздействии. В данном случае ошибка по скорости 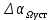 составляет 10,67 мин. составляет 10,67 мин.На рис. 5.2.5 показан график ошибки, полученный при линейно возрастающем моменте сопротивления Мс. Из графика следует, что влияние возмущающего воздействия сказывается на динамической точности ЭП, а моментная составляющая ошибки 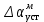 составляет 0,46 мин по истечении 4 с. При ступенчатом возмущающем воздействии моментная составляющая установившейся ошибки составляет 0,46 мин по истечении 4 с. При ступенчатом возмущающем воздействии моментная составляющая установившейся ошибки 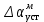 будет равна нулю. будет равна нулю.6. Аналитический способ синтеза регулятора положения6.1. Программная реализации регулятора положения для электропривода с астатизмом второго порядка. Моделирование контураположенияНачальные данные: – максимальная угловая скорость нагрузки Ωmax = 44 град/с; – максимальное угловое ускорение нагрузки εmax = 11 град/с2; – ошибка по скорости = 25 мин; – ошибка по ускорению = 50 мин ( 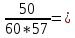 ; ;– передаточное число редуктора i1 = 203; – показатель колебательности М = 1,4; – коэффициент передачи вращающегося трансформатора Kвт = 28,5В/рад. Определяем параметры желаемой передаточной функции ЭП. Коэффициент передачи по ускорению будет равен: 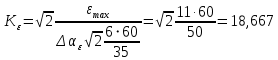 с– 2. с– 2. Значение базовой частоты определится по формуле (5.4) и будет равно: 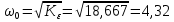 с– 1. с– 1.По выражениям (5.7) рассчитываем постоянные времени: 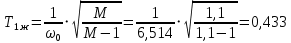 с; с;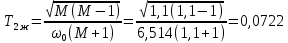 с. с.С учётом проведённых расчётов запишем желаемую передаточную функцию ЭП с астатизмом второго порядка: 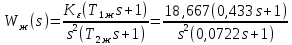 . (6.2) . (6.2)Передаточная функция неизменяемой части: 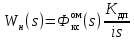 . .Так как контур скорости настроен на оптимум по модулю, то передаточная функция замкнутого контура может быть записана в виде: 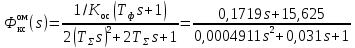 . . Тогда 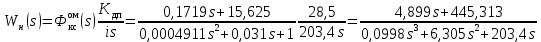 . .Для определения передаточной функции регулятора положения составляем следующую программу: num1=[18.667*0.433 18.667]; den1=[0.0722 1 0 0]; sys1=tf(num1, den1); num2=[4.899 445.313]; den2=[0.0998 6.305 203.4 0]; sys2=tf(num2, den2); sys3=sys1/sys2 sys3 = 0.8067 s^4 + 52.83 s^3 + 1762 s^2 + 3797 s ------------------------------------------ 0.3537 s^4 + 37.05 s^3 + 445.3 s^2 Полученную передаточную функцию регулятора положения можно упростить: num=[ 0.8067 52.83 1762 3797 0]; den=[0.3537 37.05 445.3 0 0]; sys=tf(num, den); minreal(sys) ans = 2.281 s^3 + 149.4 s^2 + 4982 s + 1.074e04 ----------------------------------------- s^3 + 104.7 s^2 + 1259 s Для определения передаточной функции цифрового регулятора положения 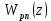 с применением формулы трапеций составим программу: с применением формулы трапеций составим программу:num=[2.281 149.4 4982 1.074e04]; den=[1 104.7 1259 0]; fs=1000; [numd, dend]=bilinear(num, den, fs) numd = 2.2390 -6.5704 6.4285 -2.0971 dend = 1.0000 -2.8993 2.7999 -0.9005 Коэффициенты матриц векторно-матричной формы записи уравнений цифрового регулятора скорости получим с применением программы: num=[2.2390 -6.5704 6.4285 -2.0971]; den=[1.0000 -2.8993 2.7999 -0.9005]; [A, B, C, D]=tf2ss(num, den) A = 2.8993 -2.7999 0.9005 1.0000 0 0 0 1.0000 0 B = 1 0 0 C = -0.0789 0.1595 -0.0809 D = 2.2390 Переходим к построению и моделированию ССДМ ЭП, показанной на рис. 6.1.1.
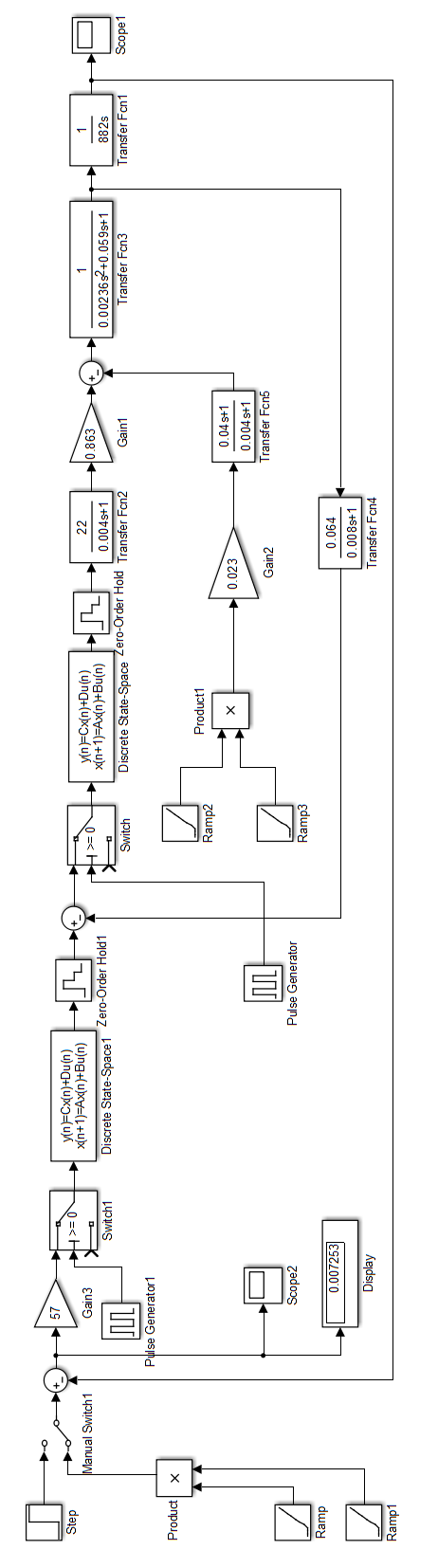 Для формирования квадратично возрастающих воздействий 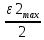 и и  используются, соотвтетственно, блоки Ramp, Ramp1 и Ramp2, Ramp3. Результаты моделирования показаны на рис. 6.1.2-6.1.4. используются, соотвтетственно, блоки Ramp, Ramp1 и Ramp2, Ramp3. Результаты моделирования показаны на рис. 6.1.2-6.1.4. α(t), рад 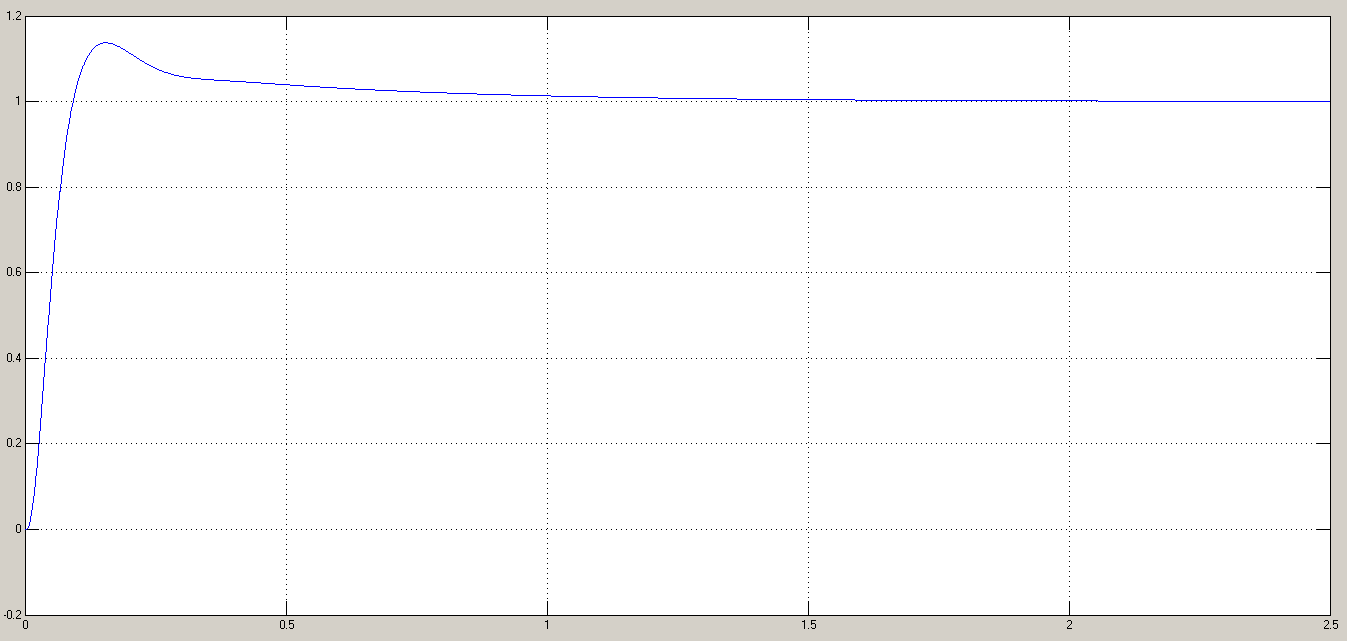 t, c t, cРис. 6.1.2. Переходная характеристика системы по задающему воздействию 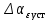 , рад , рад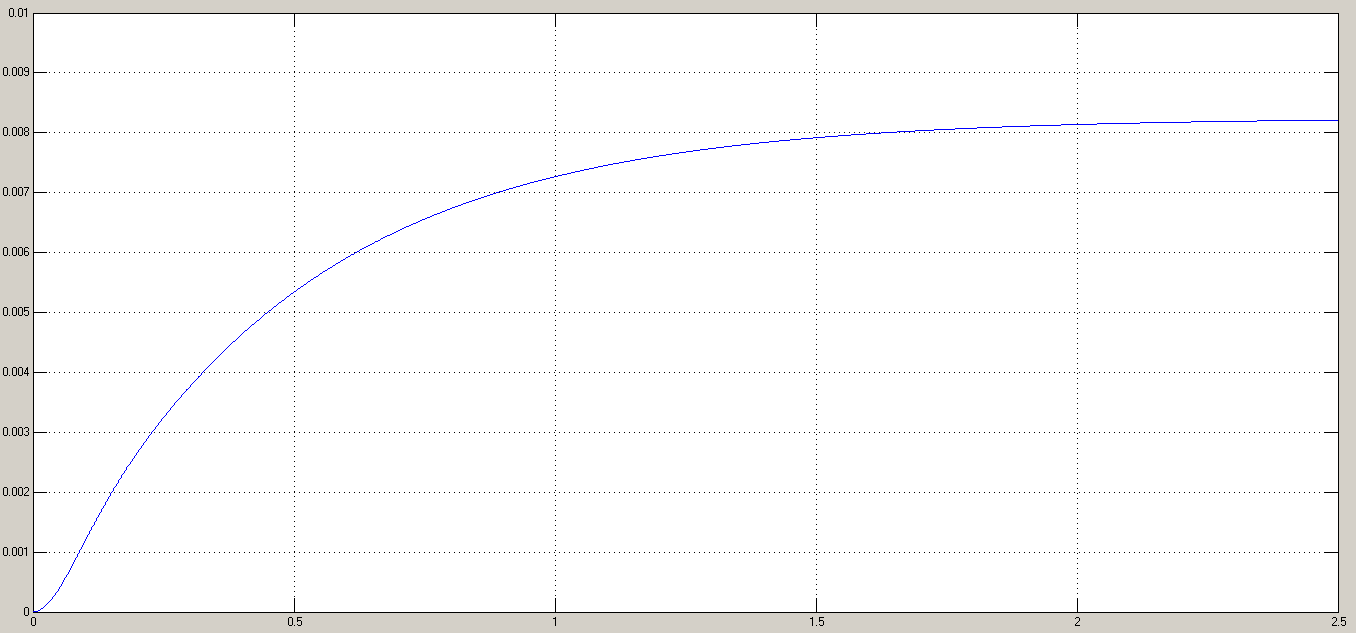 t, c t, cРис. 6.1.3. График ошибки системы при квадратично возрастающем задающем воздействии  , рад , рад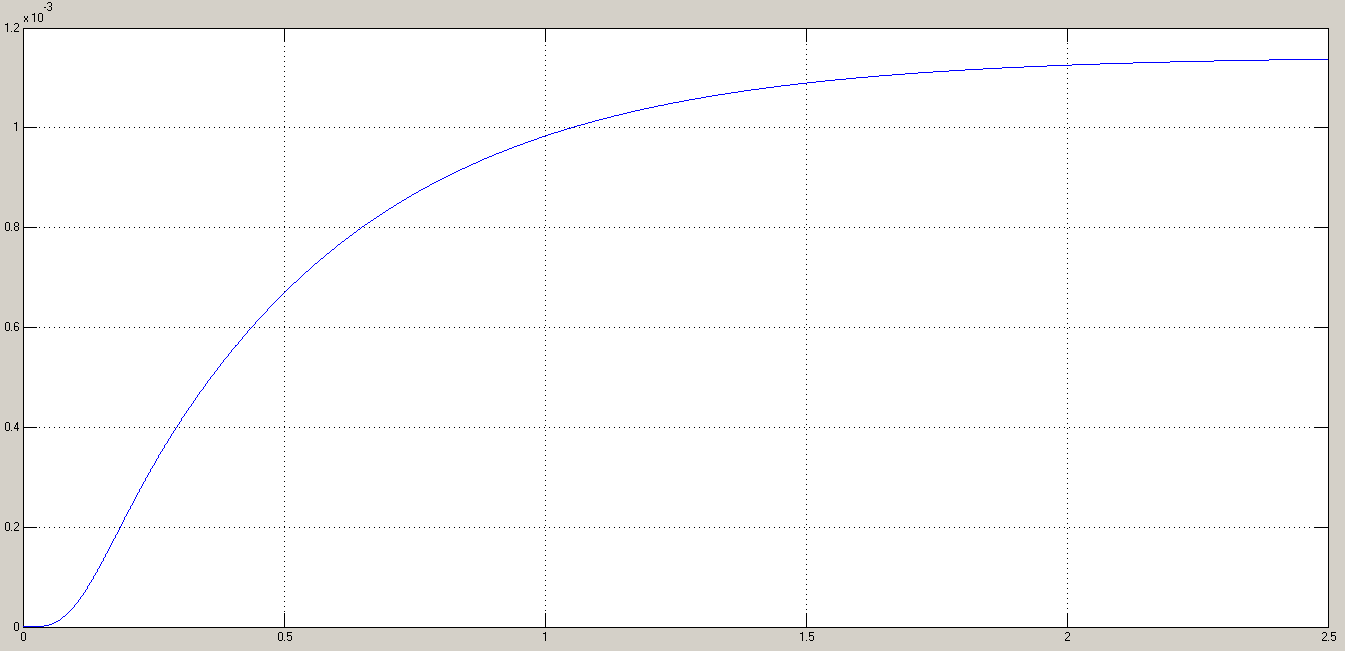 t, c t, cРис. 6.1.4. График моментной составляющей ошибки системы при квадратично возрастающем моменте сопротивления Анализ графика (рис. 6.1.2) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие 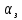 примерно за 4,0 с с перерегулированием примерно за 4,0 с с перерегулированием 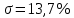 и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1. и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1.Поскольку контур положения содержит ПИД-регулятор положения, очевидно, что при ступенчатом и линейно возрастающем задающем воздействии статическая ошибка и ошибка по скорости будут равны нулю. На рис. 6.1.3 представлена характеристика при отработке типового задающего воздействия 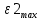 /2. Установившаяся ошибка системы /2. Установившаяся ошибка системы 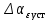 составляет около 28 мин. Моментная составляющая ошибки составляет около 28 мин. Моментная составляющая ошибки 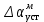 при отработке квадратично возрастающего момента сопротивления при отработке квадратично возрастающего момента сопротивления  составляет 3,8 мин по истечении 2,5 с (рис. 6.1.4). составляет 3,8 мин по истечении 2,5 с (рис. 6.1.4).ЗаключениеВ данной курсовой работе были получены следующие результаты: В 1 главе осуществили выбор двигателя, расчет параметров его передаточной функции в зависимости от соотношения постоянных времени. Произвели выбор дросселей, тиристоров и определи его передаточную функцию. Выбрали тахогенератор, и рассчитали элементы RC-фильтра. Во 2 главе вычислили установившиеся ошибки нескорректированного контура скорости. Для подтверждения расчетов установившихся ошибок использовали приёмы моделирования с получением графиков угловой скорости. В 3 главе произвели синтез пропорционально-интегрально-дифференциального регулятора скорости (ПИД-регулятора), рассчитали параметры передаточной функции и RC-элементов электрической схемы. Для подтверждения правильности синтеза ПИД-регулятора проводили моделирование оптимизированного контура скорости во временной и частотной областях. В 4 главе провели дискретную аппроксимацию передаточной функции ПИД-регулятора скорости в z-форме с применением формулы трапеций. В 5 главе произвели синтез аналоговых регуляторов положения графоаналитическим методом для систем с астатизмом первого и второго порядка. Провели анализ результатов моделирования с целью сравнения полученных показателей качества переходных процессов и установившихся ошибок с системой исходных данных, приведённой в 1 главе. В 6 главе произвели синтез регуляторов положения для систем с астатизмом второго порядка аналитическим способом. |
