Курсовая работа по дисциплине Цифровые системы управления в мехатронике АлФахри Ф. Ф. А. М
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
2. Исследование нескорректированного контура скорости2.1. Определение суммарной установившейся ошибки электропривода с двигателем типа 2ПН90LYXL4.Определяем установившуюся ошибку относительно задающего воздействия по формуле: 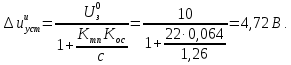 Определяем установившуюся ошибку относительно момента сопротивления по формуле: 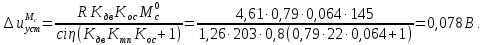 Определяем суммарную установившуюся ошибку электропривода с двигателем типа 2ПН90LYXL4: 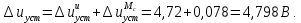 2.2. Моделирование нескорректированного замкнутого контура скорости с двигателем типа 2ПН90LYXL4. Оценка качества переходных процессов. Определение установившиеся ошибки относительно задающего воздействия и момента сопротивления. ССДМ ЭП в среде MatLab представлена на рис. 2.2.1. 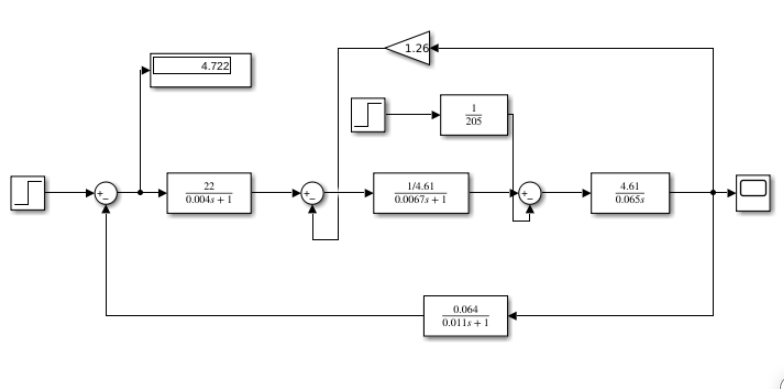 Рис. 2.2.1. ССДМ нескорректированного контура скорости На рис. 2.2.2 представлена зависимость угловой скорости от времени нескорректированного контура скорости. Наброс момента 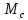 производился через 0,5 с после пуска системы «преобразователь – двигатель». производился через 0,5 с после пуска системы «преобразователь – двигатель». Из графика видно, что установившееся значение скорости двигателя без нагрузки составляет 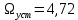 рад/с. За счет влияния рад/с. За счет влияния 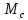 угловая скорость уменьшилась примерно на 3,4 рад/c. угловая скорость уменьшилась примерно на 3,4 рад/c.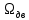 , рад/с , рад/с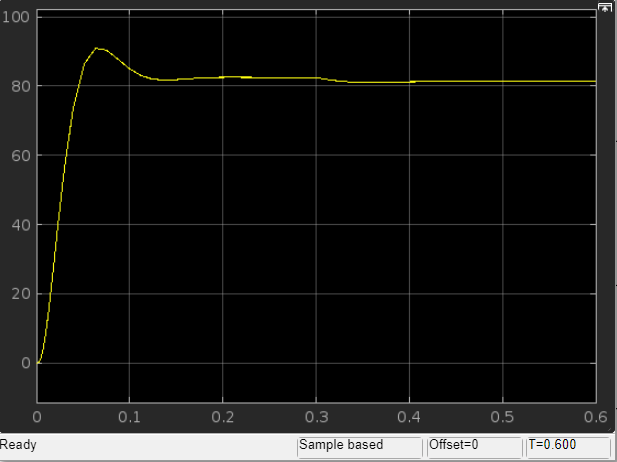 t, c t, cРис. 2.2.2. Зависимость угловой скорости от времени нескорректированного контура скорости График характеризует колебательную систему с перерегулированием около 16 % и числом колебаний N = 1 и. Время протекания переходного процесса составляет 0,4 с. Наличие колебаний обусловлено комплексно-сопряженными корнями характеристического уравнения замкнутой системы. Установившиеся ошибки по задающему воздействию и по моменту сопротивления, которые составили: 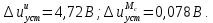 Таким образом, суммарная установившаяся ошибка электропривода с двигателем типа 2ПН90LYXL4: 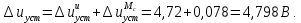 Результаты моделирования подтверждают правильность расчетов, проведенных в примере 2.1а. 3. Оптимизация контура скорости 3.1. Расчёт параметров и электрической схемы аналогового ПИД-регулятора. Выбор RC-элементов и операционного усилителя. 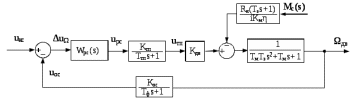 Поскольку, 4Тэ меньше, чем Тм, то передаточную функцию регулятора скорости представим в виде: 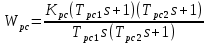 где постоянные времени 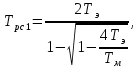 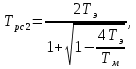  коэффициент передачи 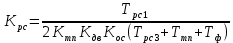 На основании схемы, представленной на рис. 3.9, постоянные времени и коэффициент передачи ПИД-регулятора скорости определяются по формулам: 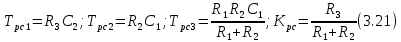 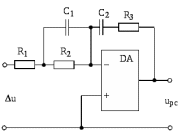 Рис. 3.9. Электрическая схема ПИД-регулятора скорости Заметим, что в формулах (3.21) число неизвестных 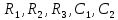 превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему. превышает число уравнений. Поэтому в инженерной практике прибегают к способу, когда значении емкостей назначаются из стандартного ряда 1; 10; 22; 33; 47; 100 мкФ. Тогда порядок расчета сводится к следующему.Задаемся емкостью 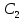 и рассчитываем и рассчитываем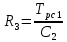 . .Задаемся емкостью 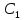 и рассчитываем и рассчитываем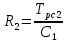 . .Согласно формуле 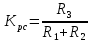 сопротивление сопротивление  . .Переходим к расчету номинальных значений RC-элементов. Постоянные времени РС:  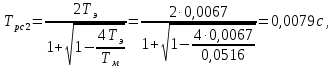 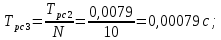 Коэффициент передачи регулятора скорости: 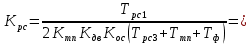 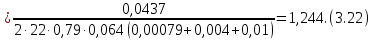 Задаем 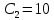 мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда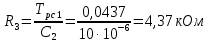 Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем  кОм. кОм.Задаем  мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда мкФ и по табл. П6 выбираем конденсатор Panasonic серии NHG. Тогда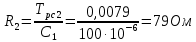 Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем 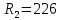 Ом. Ом.Рассчитываем сопротивление:  Приводим сопротивление к номинальному значению по ряду Е192 (см. табл. П5) и принимаем 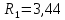 4 кОм. 4 кОм.По полученным номинальным значениям сопротивлений РС пересчитываем коэффициент передачи 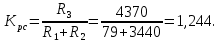 Полученное значение не отличается от величины коэффициента передачи 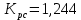 , поэтому подстройки резистора , поэтому подстройки резистора 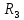 не требуется. не требуется.3.2. Проведение моделирования КС с аналоговым ПИД-регулятором скорости. Получение графиков переходных функций по задающему воздействию и по моменту сопротивления нагрузки 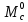 . Построение графиков ЛЧХ разомкнутого КС. Проведение анализа результатов моделирования. . Построение графиков ЛЧХ разомкнутого КС. Проведение анализа результатов моделирования. Для моделирования построим ССДМ КС в системе Simulink, представленную на рис. 3.10.  Рис. 3.10. Структурная схема динамической модели контура скорости в системе Simulink В блоке Step задаём воздействие, равное входному напряжению суммирующего усилителя КС  В, а в блоке Step 1 значение момента сопротивления нагрузки В, а в блоке Step 1 значение момента сопротивления нагрузки 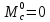 . На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию. . На рис. 3.11 изображен график переходной характеристики контура скорости по управляющему воздействию.Для построения переходной характеристики по моменту сопротивления нагрузки Мс устанавливаем соответственно в блоке Step входное воздействие 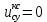 В, а в блоке Step 1 – момент сопротивления В, а в блоке Step 1 – момент сопротивления 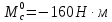 .. Полученная зависимость представлена на рис. 3.12. .. Полученная зависимость представлена на рис. 3.12. Ω(t), рад/с 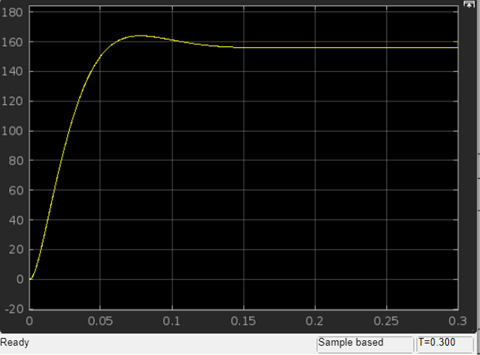 t,c t,cРис. 3.11. График зависимости угловой скорости от времени скорректированного контура скорости по сигналу задания Ω(t), рад/с 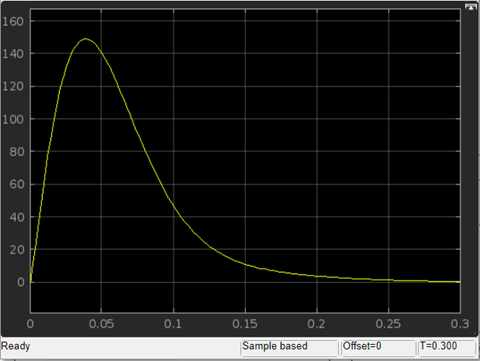 t, c t, cРис. 3.12. График зависимости угловой скорости от времени скорректированного контура скорости по моменту сопротивления Переходим к анализу полученных графиков. По графику на рис. 3.11 определяем перерегулирование: 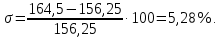 Перерегулирование, полученное в результате моделирования, отличается от требуемого значения 4,3 %. Такое изменение обусловлено влиянием малой постоянной времени Тф. Если принять Тф = 0, то перерегулирование будет равно 4,3 %, а передаточная функция ТГ представится безынерционным звеном: Wос(s) = Кос. При этом суммарную малую постоянную времени КС следует рассчитывать по формуле: 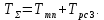 Время нарастания 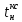 определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет: определяется в первой точке пересечения графика переходной функции и установившегося значения угловой скорости Ωуст и составляет: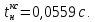 Проверяем соответствие полученного значения требованиям настройки на ОМ: 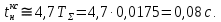 Из анализа графика на рис. 3.12 следует, что при воздействии неизменного по величине момента сопротивления Мс моментная составляющая ошибки ΔΩм примерно через 0,4 с становится равной нулю. Это говорит о том, что искусственная механическая характеристика стала абсолютно жёсткой. Увеличение точности обусловлено наличием в структуре регулятора скорости интегральной составляющей. Далее переходим к построению ЛЧХ: num1=[0.0004 0.064 1.244]; den1=[0.000034 0.0437 0]; sys1=tf(num1,den1) num2=[22]; den2=[0.004 1]; sys2=tf(num2,den2) num3=[0.79];[ den3=[0.00034 0.0516 1]; sys3=tf(num3,den3) num4=[0.064]; den4=[0.011 1]; sys4=tf(num4,den4) sys5=sys1*sys2*sys3*sys4 sys5 = 0.0004449 s^2 + 0.07119 s + 1.384 --------------------------------------------------------------------------------------- 5.086e-13 s^6 + 9.043e-10 s^5 + 3.615e-07 s^4 + 5.287e-05 s^3 + 0.002944 s^2 + 0.0437 s num = [0.0004449 0.07119 1.384]; den = [5.086e-13 9.043e-10 3.615e-07 5.287e-05 0.002944 0.0437 0]; bode(num, den) Результаты моделирования представлены на рис. 3.12. Из анализа графиков видно, что запасы устойчивости по фазе и амплитуде составляют Lз = 16,8 дБ (Gain Margin) и 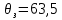 (Phase Margin) соответственно. (Phase Margin) соответственно.Значение фазы 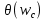 соответствует частоте среза ωс, т. е. точке пересечения графика ЛАЧХ с линией 0 дБ. соответствует частоте среза ωс, т. е. точке пересечения графика ЛАЧХ с линией 0 дБ.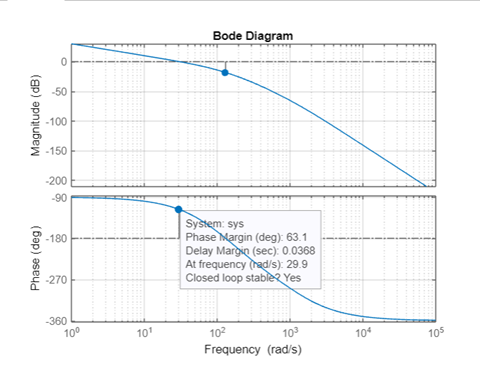 Рис. 3.12. Логарифмические частотные характеристики контура скорости Вывод: результаты моделирования подтверждают правильность расчёта параметров РС и позволяют сделать вывод о том, что КС настроен на ОМ. 5. Синтез аналогового регулятора положения (графоаналитический метод) 5.1. Синтез регулятора положения в системе с астатизмом второго порядка максимальная угловая скорость нагрузки Ωmax = 44 град/с; максимальное угловое ускорение нагрузки εmax = 11 град/с2; яшибка по скорости = 25 мин; ошибка по ускорению = 50 мин передаточное число редуктора i1 = 203; показатель колебательности М = 1,4; коэффициент передачи вращающегося трансформатора Kвт = 28,5В/рад. Моментная составляющая ошибки 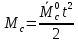 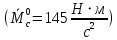 . . Определяем параметры желаемой передаточной функции ЭП. Коэффициент передачи по ускорению будет равен: 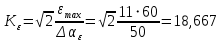 с– 2. с– 2. Значение базовой частоты определится по формуле: 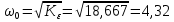 с– 1. с– 1. По выражениям рассчитываем постоянные времени: 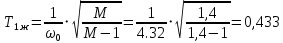 с; с; 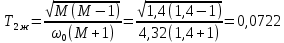 с. с.С учётом проведённых расчётов запишем желаемую передаточную функцию ЭП с астатизмом второго порядка: 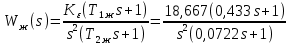 . (5.13) . (5.13)Передаточная функция неизменяемой части: 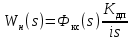 . .Данные для определения передаточной функции 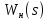 примем по примеру 3.2 и составим программу: примем по примеру 3.2 и составим программу:num1=[0.0004 0.064 1.244]; den1=[0.000034 0.0437 0]; sys1=tf(num1,den1) num2=[22]; den2=[0.004 1]; sys2=tf(num2,den2) num3=[0.79]; den3=[0.00034 0.0516 1]; sys3=tf(num3,den3) sys4=sys1*sys2*sys3; num5=[0.064]; den5=[0.01 1]; sys5=tf(num5,den5); sys6=feedback(sys4,sys5); num7=[28.5]; den7=[203.4 0]; sys7=tf(num7,den7); sys8=sys6*sys7 sys8 = 0.001981 s^3 + 0.5151 s^2 + 37.86 s + 616.2 ------------------------------------------------------------ 9.405e-11 s^7 + 1.681e-07 s^6 + 6.828e-05 s^5 + 0.01025 s^4 + 0.6805 s^3 + 23.37 s^2 + 281.4 s В приведенной программе оператор feedback осуществляет операцию замыкания отрицательной обратной связи контура скорости согласно уравнению: 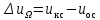 . .Для определения передаточной функции регулятора положения составляем следующую программу: num1=[18.667*0.433 18.667]; den1=[0.0722 1 0 0]; sys1=tf(num1, den1); num2=[0.001981 0.5151 37.86 616.2]; den2=[9.405e-11 1.681e-07 6.828e-05 0.01025 0.6805 23.37 281.4 0]; sys2=tf(num2, den2); sys3=sys1/sys2 sys3 = 7.602e-10 s^8 + 1.36e-06 s^7 + 0.000555 s^6 + 0.08412 s^5 + 5.692 s^4 + 201.6 s^3 + 2711 s^2 + 5253 s ------------------------------------------------------------------------------ 0.000143 s^6 + 0.03917 s^5 + 3.249 s^4 + 82.35 s^3 + 616.2 s^2 Составляем программу для определения ЛАЧХ регулятора положения, изображенную на рис. 5.2: num=[7.602e-10 1.36e-06 0.000555 0.08412 5.692 201.6 2711 5253 0]; den=[0.000143 0.03917 3.249 82.35 616.2 0 0]; bode(num, den) 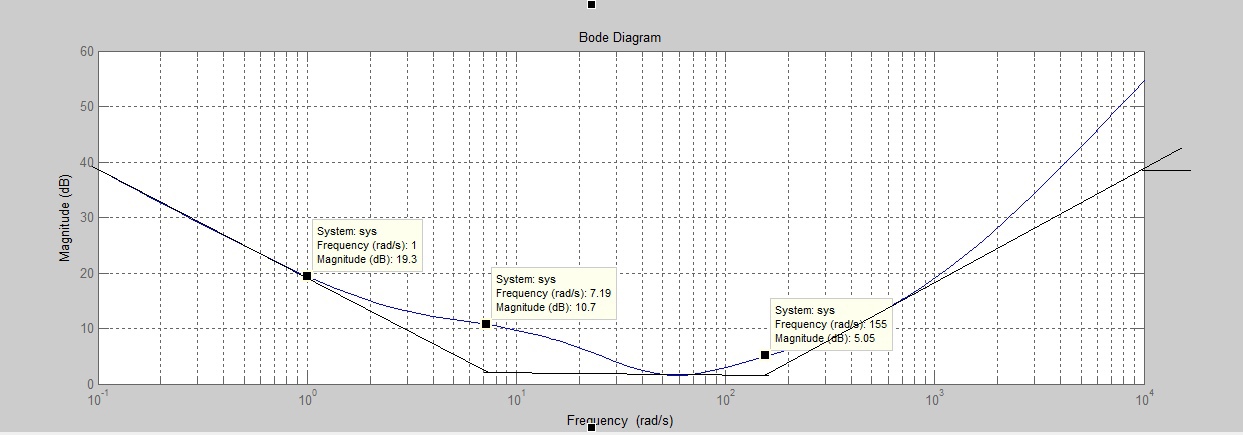 Рис. 5.2. ЛАЧХ регулятора положения Переходим к анализу полученного графика. Низкочастотный участок ЛАЧХ регулятора положения проходит под наклоном –20 дБ/дек, постепенно изменяя наклон к среднечастотному участку до 0 дБ/дек. Высокочастотный участок полученной ЛАЧХ ( 100 с– 1) аппроксимируем двумя асимптотами с наклоном 20 дБ/дек и 0 дБ/дек. Таким образом, проведённый анализ показывает, что ЛАЧХ следует аппроксимировать четырьмя асимптотами и придать регулятору положения свойства ПИД-регулятора. Рассчитаем параметры передаточной функции регулятора положения. На частоте = 1 находим: 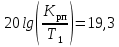 дБ, дБ,откуда  = 9,2257 с– 1. = 9,2257 с– 1.По графику, представленному на рис. 5.2, определяем частоты сопряжения 1 = 7,19 с– 1; 2 = 155 с– 1; 3 = 10000 с– 1 и рассчитываем постоянные времени: 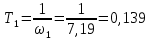 с; с; 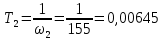 с; с; 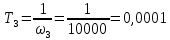 с. с.Подставляя значение Т1, получаем коэффициент передачи регулятора положения: 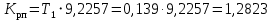 . .С учётом полученных значений передаточная функция синтезированного регулятора положения принимает вид: 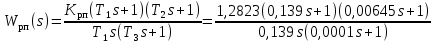 . .Для построения динамической модели ЭП представим передаточную функцию РП (ПИД-регулятора) в виде произведения:  . .
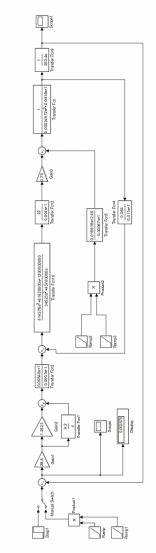 Результаты моделирования показаны на рис. 5.1.3-5.1.5. α(t), рад 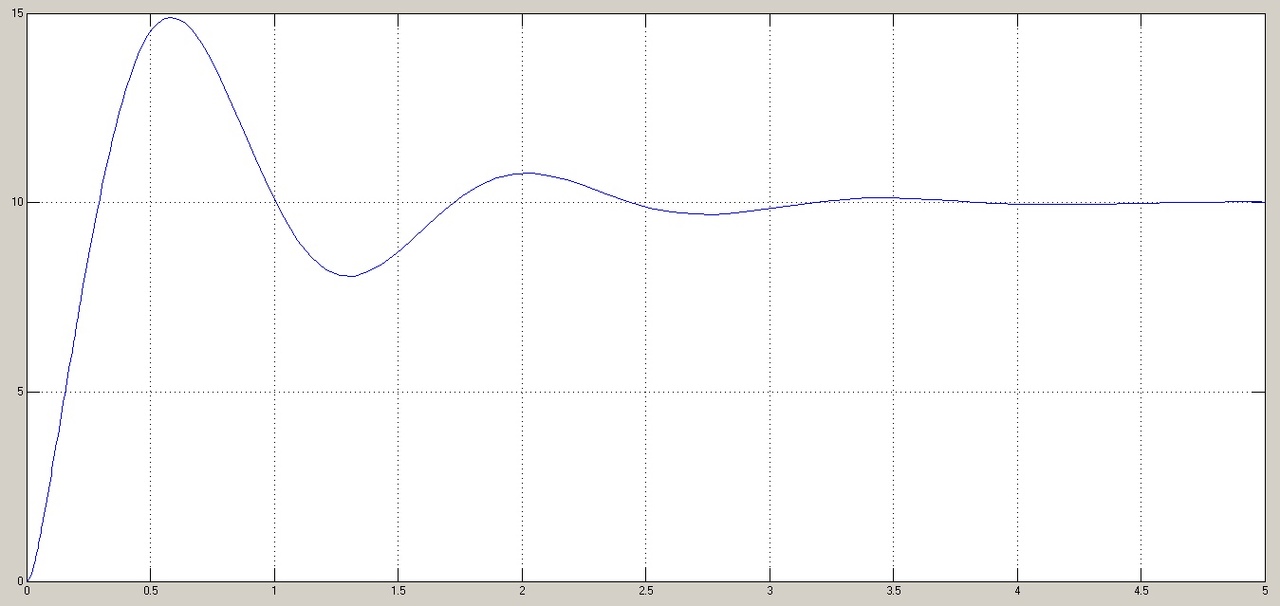 t, c t, cРис. 5.1.3. Переходная характеристика системы по задающему воздействию 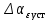 , рад , рад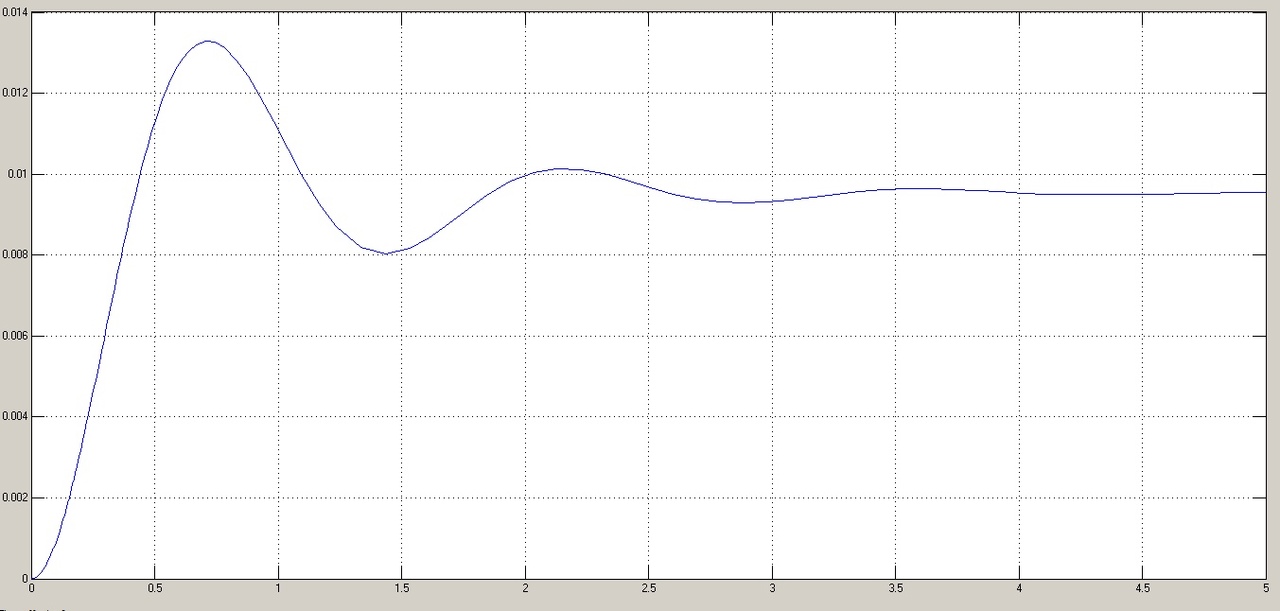 t, c t, cРис. 5.1.4. График ошибки системы при квадратично возрастающем задающем воздействии  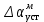 , рад , рад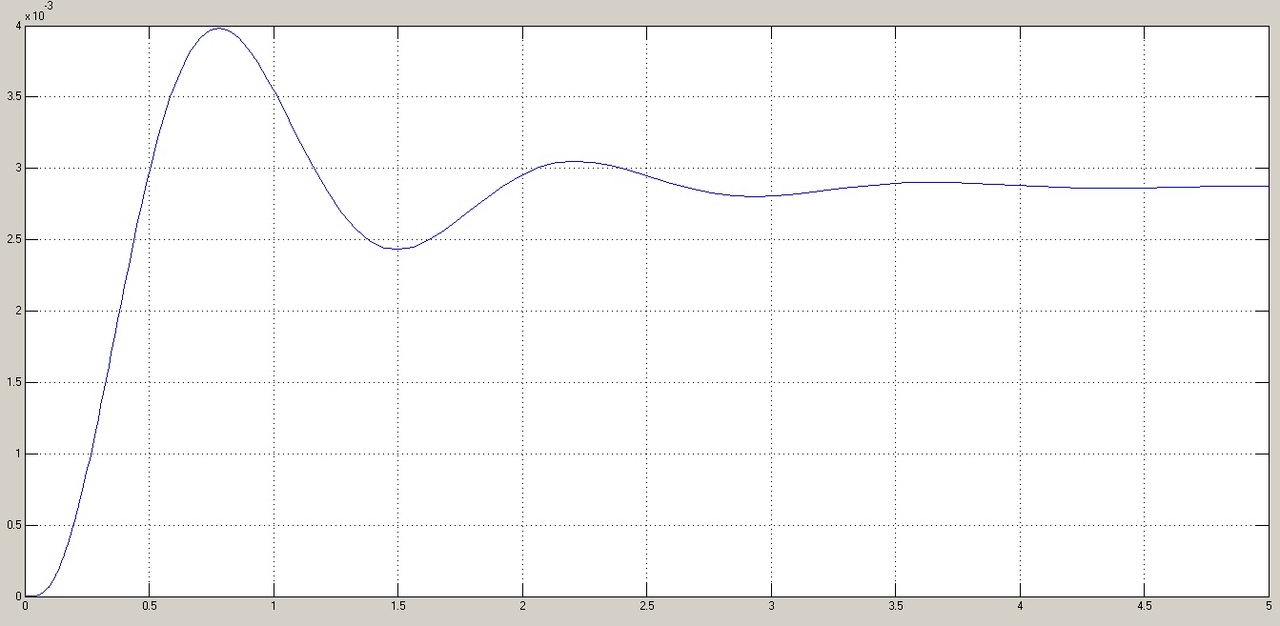 t, c t, cРис. 5.1.5. График моментной составляющей ошибки системы при квадратично возрастающем моменте сопротивления Анализ графика (рис. 5.1.3) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие  примерно за 2,0 с с перерегулированием примерно за 2,0 с с перерегулированием  и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1. и числом колебаний N < 1, что соответствует заданному показателю колебательности М = 1,1.Поскольку контур положения содержит ПИД-регулятор положения, очевидно, что при ступенчатом и линейно возрастающем задающем воздействии статическая ошибка и ошибка по скорости будут равны нулю. На рис. 5.1.4 представлена характеристика при отработке типового задающего воздействия 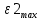 /2. Установившаяся ошибка системы /2. Установившаяся ошибка системы 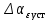 составляет примерно 25,44 мин. Моментная составляющая ошибки составляет примерно 25,44 мин. Моментная составляющая ошибки 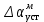 при отработке квадратично возрастающего момента сопротивления при отработке квадратично возрастающего момента сопротивления  составляет 3,3 мин по истечении 2,5 с (рис. 5.1.5). составляет 3,3 мин по истечении 2,5 с (рис. 5.1.5). |
