Курсовая. Курсовая работа по дисциплине Физические основы получения информации
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
4-5K, что вполне соответствует эксперименту). За это открытие в 1998 году Лафлину, Штермеру и Тсуи была вручена нобелевская премия по физике. В настоящее время проблема двумерной электронной жидкости по прежнему актуальна в современной физике. 3.5 Измерение ЭДС Холла Датчик ЭДС Холла – это элемент автоматики, радиоэлектроники и измерительной техники, используемый в качестве измерительного преобразователя, действие которого основано на эффекте Холла. Представляет собой тонкую прямоугольную пластину (площадь – несколько мм2), или пленку, изготовленную из полупроводника (Si, Ge, InSb, InAs), имеет четыре электрода для подвода тока и съема ЭДС Холла. Чтобы избежать механических повреждений, пластинки Холла ЭДС датчика монтируют (а пленку напыляют в вакууме) на прочной подложке из диэлектрика (слюды, керамики). Для получения наибольшего эффекта толщина пластины (пленки) делается возможно меньшей. Датчики ЭДС Холла применяют для бесконтактного измерения магнитных полей (от 10-6 до 105 Э). При измерении слабых магнитных полей пользуются Холла ЭДС датчиками, вмонтированными в зазоре ферро– или ферримагнитного стержня (концентратора), что позволяет значительно повысить чувствительность датчика. Так как в полупроводниках концентрация носителей зарядов (а, следовательно, и коэффициент Холла) может зависеть от температуры, то в случае точных измерений необходимо либо термостатировать Холла ЭДС датчик, либо применять сильнолегированные полупроводники (последнее снижает чувствительность датчика). 4 Магнитное поле катушек Гельмгольца Получение однородного магнитного поля в определенном объеме это задача, часто встречающаяся в постановке физического эксперимента. В зависимости от требуемой величины магнитной индукции B, размеров рабочей области, мощности установки, веса и конструктивных требований эта проблема решается разными способами. Магнитное поле может быть создано с помощью катушек с током, электромагнитов и постоянных магнитов. Постоянные магниты не требуют энергии, но не дают возможности эффективно и просто управлять величиной магнитного поля. Величина получаемой магнитной индукции для них определяется остаточной намагниченностью материала магнита и для разных материалов может иметь разные значения до величин порядка тесла (максимально – 1.38 Тл для магнитов Nd-Fe-B). Постоянные магниты широко применяются в приборах электронной техники, где требуется неизменное поле определенной величины. В лабораторной практике, где энергозатраты не являются главным критерием, а важно удобство управления, более распространены первые два метода – магнитное поле создается с помощью катушек с током и электромагнитов. Рассмотрим особенности этих методов получения магнитного поля. Для получения относительно слабых полей, модуль вектора магнитной индукции которых не превышает 0.1 Тл (В ≤ 0,1Тл) чаще всего применяют катушки с током, при этом поле высокой степени однородности (В = const) можно получить, используя соленоид или катушки Гельмгольца. При указанных величинах магнитной индукции (В) магнитное поле может быть получено сравнительно небольшими токами, которые легко генерируются лабораторными средствами. Поля средней величины ( 0.1 ≤ В ≤ 1 Тл) получить предыдущим способом труднее, поскольку требуемые при этом токи пропорционально возрастают, а рассеиваемая тепловая мощность и мощность источников питания растет как квадрат тока, что порождает ряд технических проблем. Для получения таких полей в лабораторной практике широко используются электромагниты, т.е. катушки с током, одетые на ферромагнитный сердечник, чаще всего из железа. Относительная магнитная проницаемость железа может достигать величины нескольких тысяч (у чистого железа до 20000). Таким образом, сравнительно малым током можно вызвать большую намагниченность сердечника и получить в зазоре электромагнита магнитное поле с величиной индукции на несколько порядков большей, чем она была бы в такой же катушке без сердечника. Физическим ограничением для получения сильных полей данным методом является величина магнитной индукции насыщения магнетика, достигая которую, магнетик перестает вносить дальнейший вклад в величину магнитного поля (для железа индукция насыщения равна 2.18 Тл). По этой причине для получения сильных магнитных полей порядка десятков тесла применение магнитных сердечников теряет смысл, поскольку такие поля намного превосходят намагниченность насыщения всех известных ферромагнетиков. Поэтому для получения сильных полей используются только катушки с током. Проблемы мощности решаются либо применением кратковременного, импульсного, режима работы, либо использованием сверхпроводящих катушек. Подобно постоянным магнитам, сверхпроводящие магниты после возбуждения поля теоретически не требуют энергии. Однако значительная мощность должна тратиться на охлаждение обмоток, поскольку известные в настоящее время и пригодные к изготовлению катушек материалы обладают сверхпроводимостью только при низких, криогенных температурах. Например, сверхпроводящие магниты Большого адронного коллайдера дают индукцию до 8.5 Тл при температуре жидкого гелия. В настоящее время сверхпроводящие магниты позволяют получить поля свыше 20 Тл. Катушками Гельмгольца называется система из двух одинаковых тонких катушек, расположенных соосно на расстоянии, равном их радиусу. В пространстве между катушками с электрическим током получается магнитное поле высокой однородности, причем, в отличие от магнитного поля соленоида, доступ в рабочую область открыт со всех сторон. Платой за это удобство является проигрыш в величине поля при том же токе и числе витков. Магнитную индукцию в центре одного витка (ток идет только по одной катушке) системы можно рассчитать по формуле: 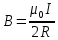 (25) (25)5 Измерение магнитного поля соленоидов Все магнитометры функционально можно разделить на две группы - магнитометры для измерения внешних магнитных полей или иначе, полей, создаваемых объектами и магнитометры для исследования магнитных свойств вещества. Несмотря на то, что магнитометры, входящие в первую и вторую группы функционально различны, и конструктивно отличаются друг от друга, в них могут быть применены одни и те же физические явления. В связи с этим рассмотрим классификацию магнитометров, исходя из законов, лежащих в основе их работы. Их можно разделить на пять основных групп: Феррозондовые; Магнитоиндуктивные; Магниторезисторные; Квантовые; На основе эффекта Холла. Датчик Холла. Для проведения регулярных измерений необходим простой в эксплуатации и дешевый прибор. Для измерения индукции магнитного поля широкое применение нашли датчики на основе эффекта Холла, один из которых используется в настоящей работе для исследования магнитного поля соленоидов. Для понимания эффекта Холла рассмотрим проводник в форме призмы, шириной b и толщиной d, рис. 11. Пусть электрический ток I (традиционно – это движение положительных зарядов) от источника питания И.П. направлен вдоль оси Z, от контакта 1 к контакту 2. При этом верхняя грань C и нижняя грань D, соответственно вверху и внизу призмы, симметричны по отношению к току и представляют равные эквипотенциальные поверхности. Поэтому разность потенциалов между ними равна нулю, т.е. вольтметр V показывает ноль. При включении магнитного поля B, вектор индукции которого направлен параллельно оси Y , траектория движения зарядов изменится, т.е. заряды начнут отклоняться в сторону верхней грани призмы под действием силы Лоренца. В результате на нижней грани проводника сконцентрируются отрицательные заряды, а на противоположной верхней, симметрично расположенной стороне сконцентрируются положительные заряды. Между этими зарядами, как между обкладками пластин плоского конденсатора, возникнет электрическое поле напряженностью Е, которое принято называть электрическим полем Холла. Это поле, в свою очередь, воздействует на каждый заряд q с силой Кулона. 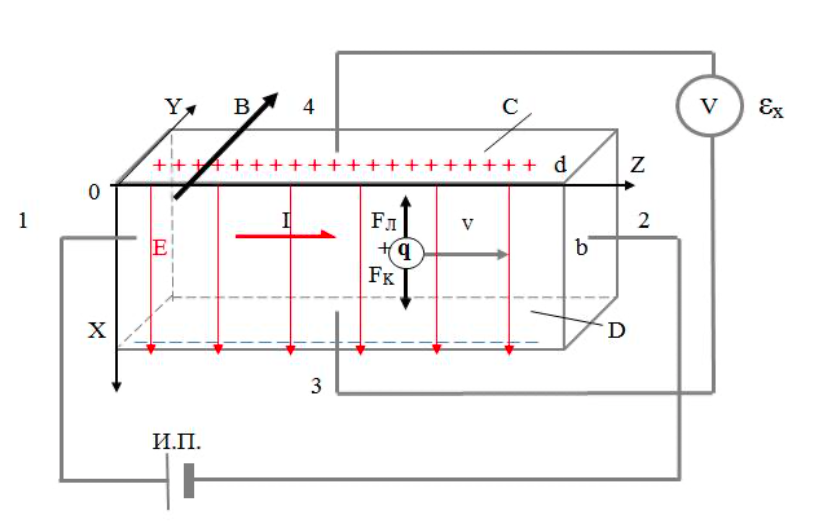 Рисунок 11 - Проводник в форме призмы Рисунок 11 - Проводник в форме призмы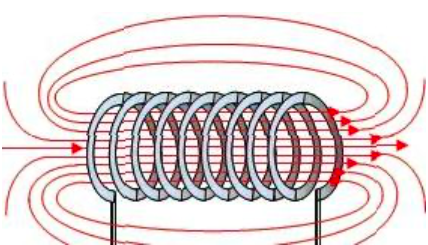 Соленоид. Рассмотри магнитное поле соленоида. Упрощенная схема соленоида, а также распределение поля вокруг соленоида показаны на рис. 12. Соленоид представляет собой обмотку из проводника с низким удельным сопротивлением, намотанную на жесткий каркас – катушку (на рисунке не показана). Обмотка может состоять из нескольких слоев намотанного провода. Конфигурация поля соленоида зависит от соотношения диаметра соленоида к его длине. Принято считать соленоид длинным, при его длине, превышающей его диаметр более, чем в десять раз. В таком соленоиде внутри обмотки поле однородно, а величина индукции в средней части соленоида в два раза выше, чем на торцах. Такой соленоид тождественен постоянному магниту в виде цилиндра. Соленоид. Рассмотри магнитное поле соленоида. Упрощенная схема соленоида, а также распределение поля вокруг соленоида показаны на рис. 12. Соленоид представляет собой обмотку из проводника с низким удельным сопротивлением, намотанную на жесткий каркас – катушку (на рисунке не показана). Обмотка может состоять из нескольких слоев намотанного провода. Конфигурация поля соленоида зависит от соотношения диаметра соленоида к его длине. Принято считать соленоид длинным, при его длине, превышающей его диаметр более, чем в десять раз. В таком соленоиде внутри обмотки поле однородно, а величина индукции в средней части соленоида в два раза выше, чем на торцах. Такой соленоид тождественен постоянному магниту в виде цилиндра.Рисунок 12 - Упрощенная схема соленоида 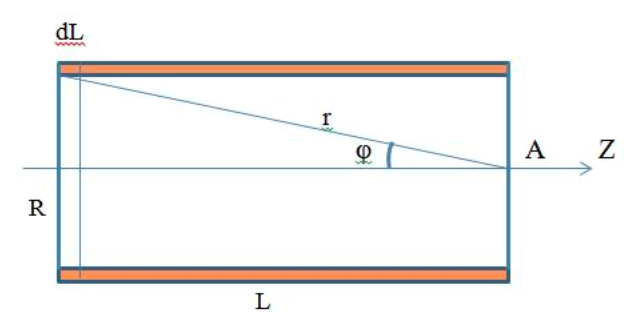 Для вывода расчетной формулы индукции магнитного поля соленоида рассмотрим рис. 13. На рисунке изображена схема соленоида с числом витков N, длиной L и радиуса R. Для упрощения вывода формулы примем толщину обмотки намного меньшей, например, в десять раз, чем его радиус. На конце обмотки выделим малый элемент обмотки длиной dL. Для вывода расчетной формулы индукции магнитного поля соленоида рассмотрим рис. 13. На рисунке изображена схема соленоида с числом витков N, длиной L и радиуса R. Для упрощения вывода формулы примем толщину обмотки намного меньшей, например, в десять раз, чем его радиус. На конце обмотки выделим малый элемент обмотки длиной dL. Рисунок 13 - Схема соленоида В соответствии с законом Био – Саварра – Лапласа индукция магнитного поля контура с током в точке А, которая находится на расстоянии L от плоскости контура, на его оси равна: 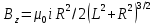 (26) (26)Где μ - магнитная постоянная, равная 4π 10-7 Гн/м, i - сила тока в контуре, R - радиус контура, L2+R2=r2 - квадратрадиус вектора, φ - угол между осью контура с током и направлением радиус - вектора в рассматриваемую точку. Перейдем от бесконечно тонкого контура с током к элементарному соленоиду длиной dL. На малой длине dL содержится N dL / L витков, по которым течет круговой ток величиной: 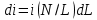 (27) (27)Тогда индукция магнитного поля в точке А для малого элемента обмотки (элементарного соленоида) будет равна: 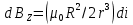 (28) (28)Обозначим отношение число витков, приходящихся на один метр длины соленоида N / L символом n. Учитывая, что dL Sin φ = r dφ, рис. 14 (элемент обмотки dL показан в укрупненном виде), где dφ – бесконечно малое приращение угла и заменив dL = rdφ/Sinφ и R=r Sinφ получим: 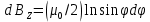 (29) (29)Интегрируя это выражение от φ до π / 2 по всей длине соленоида, рис. 13, что соответствует выполнению принципа суперпозиции полей элементарных соленоидов, получим величину магнитной индукции всего соленоида на его торце: 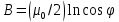 (30) (30)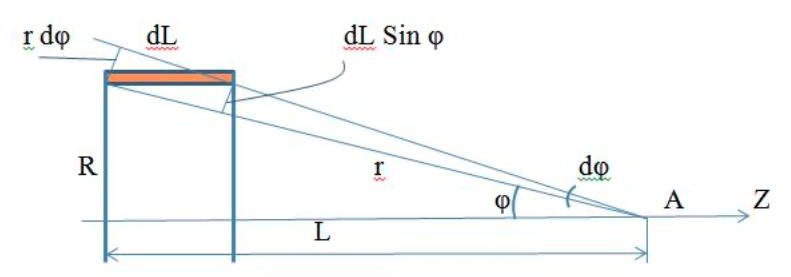 Рисунок 14 - Укрупненный вид элемента обмотки dL Из уравнения (30) видно, что при L ˃˃ R индукция магнитного поля на торце длинного соленоида равна: 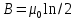 (31) (31)Для определения величины магнитной индукции за пределами соленоида, на его оси, например, в точке А рассмотрим рис. 15. Мысленно увеличим длину соленоида на величину z до точки А. Тогда соленоид будет состоять из двух соленоидов С 1 и С 2. Поле соленоида С 1 в точке А в соответствии с принципом суперпозиции полей, будет равно разности полей удлиненного соленоида С 1 + С 2 и соленоида С 2, т.е. B = (μ0 In/2) (Cosφ1 -Cosφ2 ) 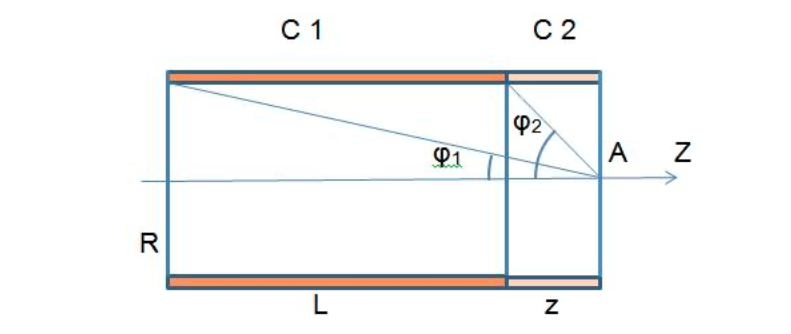 Рисунок 15 - Схема соленоида Заменив косинусы на соответствующие им выражения, получим формулу для расчета индукции магнитного поля в любой точке на оси как внутри, так и вне соленоида: 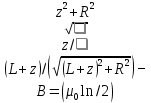 (32) (32)Из уравнения видно, что при L ˃˃ R в центре соленоида на его оси при z = - L / 2 магнитная индукция равна: 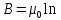 (33) (33)Сравнение двух уравнений (31) и (33) показывает, что поле в центре длинного соленоида на его оси в два раза больше чем на его торце. Единица измерения магнитной индукции является Тесла [Тл]. Тесла – это магнитная индукция такого однородного магнитного поля, в котором на проводник длиной 1 метр, при протекании через него тока в 1 Ампер действует сила Ампера в 1 Ньютон. ЗАКЛЮЧЕНИЕ Теория эффекта Холла достаточно разработана и даже обобщена на случай зонной структуры твердого тела, и вплоть до 1980 года казалось, что никаких открытий в этой области физики твердого тела не предвидится. Однако в 1980 году немецкий физик Клаус фон Клитцинг с соавторами (Klaus von Klitzing, G.Dorda, M.Pepper), измеряя Э.Д.С. Холла и магнитосопротивление в поперечном магнитном поле в гетероструктурах, обнаружили, что в сильных полях ( |

