|
|
Курсовая. Курсовая работа по дисциплине Физические основы получения информации
3.2 Эффект Холла в различных средах
 Эффект Холла в полупроводниках. Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлежности полупроводника к n- или p-типу, так как в полупроводниках n-типа знак носителей тока отрицательный, полупроводниках p-типа – положительный. Эффект Холла в полупроводниках. Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлежности полупроводника к n- или p-типу, так как в полупроводниках n-типа знак носителей тока отрицательный, полупроводниках p-типа – положительный.
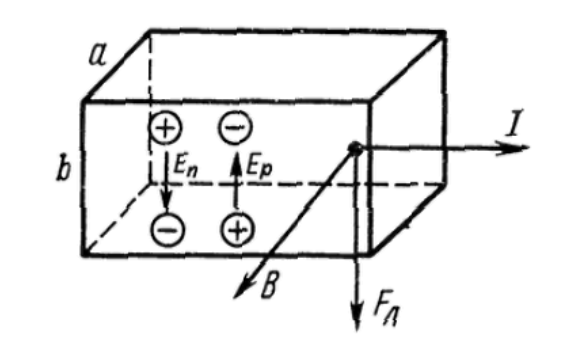
Рисунок 5 - Эффект Холла для образца с положительными и отрицательными носителями
Направление магнитной силы (силы Лоренца) изменяется на противоположное как при изменении направления движения заряда, так и при изменении его знака. Следовательно, при одинаковом направлении тока и поля магнитная сила, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней (рис. 5) грани ниже, чем нижней, а в случае отрицательных носителей — выше. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей тока.
Коэффициент Холла (для изотропных полупроводников) выражается через парциальные проводимости э и д и концентрации электронов nэ и дырок nд:
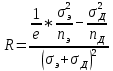 (13) (13)
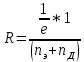 (14) (14)
Эффект Холла в ферромагнетиках. В ферромагнетиках на электроны проводимости действует не только внешнее, но и внутреннее магнитное поле. Это приводит к особому ферромагнитному или «аномальному» эффекту Холла. Экспериментально обнаружено, Ex=(RB+RаM)j, где R — обыкновенный, a Ra — необыкновенный (аномальный) коэффициент Холла. Между Ra и удельным электросопротивлением ферромагнетиков установлена корреляция. При исследовании эффекта Холла в ферромагнетиках обычно рассматривается удельное холловское сопротивление:
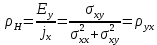 (15) (15)
Вклад в эффект Холла, пропорциональный намагниченности, получил название ферромагнитного, спонтанного или аномального эффекта Холла (АЭХ). Этот вклад существует в парамагнетиках, в ферромагнетиках выше температуры Кюри, ферри- и антиферромагнетиках, в Кондо-системах. Поэтому название «аномальный эффект Холла» является наиболее общим.
В настоящее время достаточно полно разработана теория этого явления. В этом большая заслуга отечественных ученых и, в частности, сотрудников кафедры магнетизма физического факультета МГУ, принадлежащих к школе профессора Е. И. Кондорского.
Математическое описание явлений переноса связано с установлением уравнения баланса для функции распределения, описывающей вероятность нахождения частицы в любом заданном состоянии. Уравнение баланса представляет собой сумму двух членов: полевого члена, обусловленного ускорением под действием поля, и столкновительного члена, который ограничивает это ускорение. Наиболее удобной методикой, позволяющей получить необходимые уравнения для функции распределения электронов, является метод матрицы плотности, в котором уравнение движения в обычной квантовомеханической форме после некоторого анализа могут быть сведены к кинетическим уравнениям.
Одночастичный гамильтониан электронов проводимости кристаллического ферромагнетика в нерелятивистском приближении может быть записан в виде:
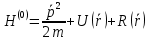 (16) (16)
Где U (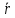 ) - периодический потенциал, создаваемый как обменным взаимодействием, так и кристаллической решеткой; R( ) - периодический потенциал, создаваемый как обменным взаимодействием, так и кристаллической решеткой; R(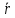 ) - потенциал рассеяния, связанный с любыми нарушениями периодичности (примеси, тепловые колебания токов, магнитные неоднородности). Если первый член гамильтониана характеризует действие силы Лоренца, то последующие свидетельствуют о том, что имеется АЭХ, пропорциональный магнитному моменту, и приводят к созданию асимметрии при рассеянии электронов проводимости, приводящей к холловскому закручиванию в отсутствии внешнего магнитного поля. Этим двум требованиям удовлетворяет спин-орбитальное взаимодействие. К возможным типам СОВ можно отнести собственное и несобственное. Собственное спин-орбитальное взаимодействие есть взаимодействие спина самого электрона с магнитным полем, которое создается при движении электрона по орбите. Несобственное СОВ является взаимодействием орбиты i-го электрона проводимости со спином другого j -го (локализованного или коллективизированного) электрона. ) - потенциал рассеяния, связанный с любыми нарушениями периодичности (примеси, тепловые колебания токов, магнитные неоднородности). Если первый член гамильтониана характеризует действие силы Лоренца, то последующие свидетельствуют о том, что имеется АЭХ, пропорциональный магнитному моменту, и приводят к созданию асимметрии при рассеянии электронов проводимости, приводящей к холловскому закручиванию в отсутствии внешнего магнитного поля. Этим двум требованиям удовлетворяет спин-орбитальное взаимодействие. К возможным типам СОВ можно отнести собственное и несобственное. Собственное спин-орбитальное взаимодействие есть взаимодействие спина самого электрона с магнитным полем, которое создается при движении электрона по орбите. Несобственное СОВ является взаимодействием орбиты i-го электрона проводимости со спином другого j -го (локализованного или коллективизированного) электрона.
Аналогично двум моделям в теории магнетизма в теории аномального эффекта Холла существуют две модели. Первая модель соответствует зонной теории магнетизма, и в ней предполагается, что носителями АЭХ являются намагниченные электроны проводимости, холловское закручивание которых связано с действием собственного спин- орбитального взаимодействия. В рамках этой теории носителями АЭФ могут быть либо намагниченные d -подобные электроны проводимости, либо слабонамагниченные s -подобные электроны. Но поскольку парциальная намагниченность s -подобных электронов много меньше намагниченности d -электронов, то рассматривается АЭХ только за счет намагниченности d -подобных электронов.
Вторая модель предполагает, что электроны, обеспечивающие магнитный момент материла, локализованы, и их подмагничивающим действием на электроны проводимости можно пренебречь. Ненамагниченные электроны проводимости являются носителями АЭХ в этом случае. Зависимость аномальной холловской проводимости от намагниченности появляется либо за счет несобственного СОВ (взаимодействие орбиты электрона проводимости со спином локализованного электрона), либо при рассеянии на магнитных неоднородностях и за счет собственно СОВ магнитных электронов внутри иона.
В рамках первой модели была решена задача о вычислении аномальной холловской электропроводности для газа блоховских намагниченных электронов при наличии малой концентрации примесей. Под влиянием СОВ при рассеянии электрона на примесном центре возникает асимметрия в вероятности рассеяния, приводящая к холловскому закручиванию. Это «ассиметричное рассеяние» (scew scattering) в низшем порядке по потенциалу рассеяния приводит к зависимости R
λρ , а в следующем – к зависимости R
λρ 2 . Поэтому ss при низких температурах при асимметричном рассеянии носителей тока для аномального коэффициента Холла имеем:
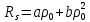 (17) (17)
Значительная температурная зависимость аномального эффекта Холла заставила рассмотреть и другие возможные механизмы рассеяния, в частности на колебаниях кристаллической решетки (фононах) и на магнитных неоднородностях (магнонах). Было показано, что в первой модели основным механизмом рассеяния, определяющим температурную зависимость, является рассеяние на фононах. Для температур выше дебаевской было получено, что Rs
λρ 2 .В модели II основным механизмом рассеяния является рассеяние на магнитных неоднородностях, которое приводит к следующей зависимости Rs
ρM, где ρM - магнитный вклад в сопротивление проводника, который при T < Tc монотонно увеличивается с повышением температуры, а при T > Tc, ρM =const.
3.3 Побочные явления эффекта Холла
Точность данных, полученных при исследовании гальваномагнитных эффектов, зависит не только от тщательного анализа результатов измерений, но и от правильного учета влияния «побочные» явлений. Так, «побочные» явления вносят вклад в измеряемое суммарное напряжение на поперечных холловских контактах:
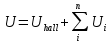 (18) (18)
 Где Uhall - ЭДС Холла, Ui - ЭДС побочных эффектов. Где Uhall - ЭДС Холла, Ui - ЭДС побочных эффектов.
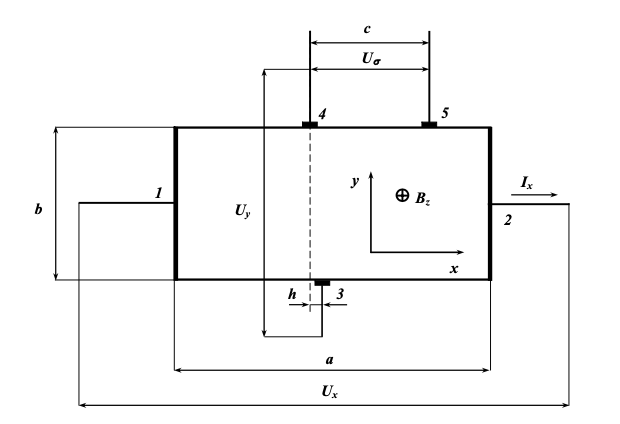
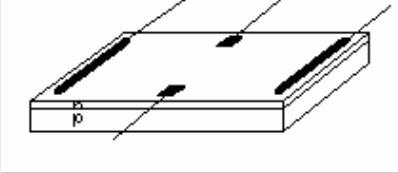
Рисунок 6 - Величины, измеряемы при исследовании эффекта Холла
Рассмотрим величины, непосредственно измеряемые при исследовании эффекта Холла в режиме ЭДС Холла на примере образца, представленного на рис. 6.
Остановимся на восьми основных источниках побочных эффектов. К ним относятся:
- ЭДС асимметрии холловских контактов UA , обусловленная падением напряжения при протекании первичного тока Ix через участок образца сопротивлением Rh , заключенного между сдвинутыми на расстояние h контактами Холла (рис. 6).
- ЭДС магниторезистивного эффекта U M ;
- термоЭДС (UT ), возникающая в холловской цепи на контактах подводящий провод-образец при различии температур в поперечном направлении между холловскими контактами;
- ЭДС Эттинсгаузена UE - термо- ЭДС в цепи холловских контактов, связанная с разностью температур на холловских гранях образца, обусловленная тем, что носители, скорость которых в скрещенных полях Ex и Bz отличается от средней, отклоняются к холловским граням, причем «быстрые» носители отдают энергию решетке образца и нагревают одну холловскую грань образца, а «медленные» пополняют свою энергию за счет охлаждения решетки на другой холловской грани;
- ЭДС Нернста-Эттинсгаузена U NE , отличающаяся от U E тем, что поток носителей обусловлен не электрическим полем Ex , а тепловым 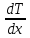 , причем носители, движущиеся от «горячего» токового электрода к «холодному», имеют большую энергию по сравнению с носителями, движущимися в обратном направлении; , причем носители, движущиеся от «горячего» токового электрода к «холодному», имеют большую энергию по сравнению с носителями, движущимися в обратном направлении;
- ЭДС Пельте-Нернста-Эттинсгаузена U PNE , отличающаяся от U NE тем, что температурное поле 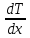 обусловлено эффектом Пельтье – выделением или поглощением теплоты при прохождении тока силы Ix через контакт токового электрода с образцом; обусловлено эффектом Пельтье – выделением или поглощением теплоты при прохождении тока силы Ix через контакт токового электрода с образцом;
- ЭДС Риги-Ледюка URL , отличающаяся от UNE тем, что в данном случаем подразумевается термомагнитный эффект – аналог эффекта Холла, в котором продольное температурное поле 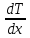 приводит кпоявлению поперечного температурного поля приводит кпоявлению поперечного температурного поля 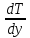 в скрещенном магнитном поле Bz ; в скрещенном магнитном поле Bz ;
- ЭДС Пельтье-Риги-Ледюка U PRL , отличающаяся от U RL тем, что температурное поле 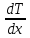 обусловлено эффектом Пельте. обусловлено эффектом Пельте.
Оценка влияния ЭДС перечисленных побочных эффектов на ЭДС Холла показывает, что самый большой вклад в измеряемую поперечную ЭДС UΣ вносят ЭДС асимметрии UA и термо-ЭДС UT . Выполняя усреднение UΣ по двум направлениям Ex и Bz , можно исключить ЭДС всех побочных явлений, кроме трех: UE , UPNE и UPRL . Поэтому для уменьшения влияния термомагнитных эффектов, необходимо принимать тщательные меры для соблюдения изотермических условий эксперимента. Термо-ЭДС может внести погрешность при измерении продольногонапряжения проводимости Uσ при наличии температурного поля 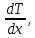 особенно в высокопроводящих образцах, когда Uσ мала. особенно в высокопроводящих образцах, когда Uσ мала.
Следует отметить, что проведенные на переходных металлах и сплавах специальные исследования показали, что U E , U PNE и U PRL составляют всего несколько процентов от ЭДС Холла. Особенно это относится к ферромагнитным металлам и сплавам.
3.4 Датчики Холла
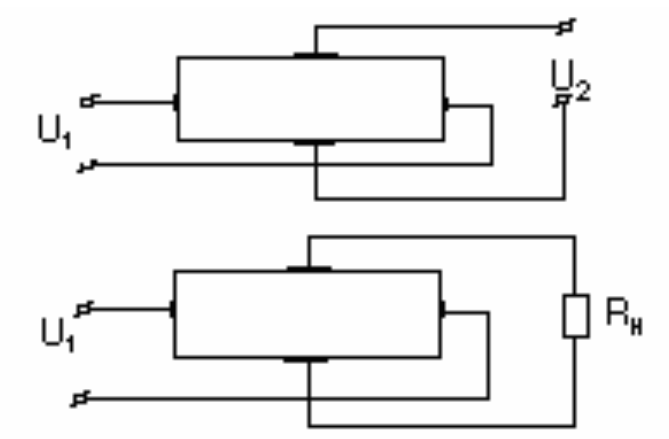 Параметры и характеристики датчиков Холла. Датчик Холла представляет собой магнитоэлектрический полупроводниковый прибор, основанный на использовании эффекта Холла, на рис. 7, а показаны схемы включения датчика Холла. Параметры и характеристики датчиков Холла. Датчик Холла представляет собой магнитоэлектрический полупроводниковый прибор, основанный на использовании эффекта Холла, на рис. 7, а показаны схемы включения датчика Холла.
Рисунок 7 - Схемы включения датчика Холла
Напряжение, подаваемое на управляющие электроды U1, называется входным напряжением датчика Холла, а сопротивление R1 между этими электродами называется входным сопротивлением. Величина этого сопротивления при отсутствии магнитного поля определяется по формуле:
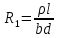 (19) (19)
Где р — удельное сопротивление полупроводника. С ростом напряженности магнитного поля входное сопротивление увеличивается. Напряжение между двумя другими (холловскими) контактами называется выходным и обозначается U2 (рис. 7). Сопротивление между холловскими контактами называется выходным и обозначается R2 . Величина его при отсутствии магнитного поля определяется выражжением:
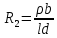 (20) (20)
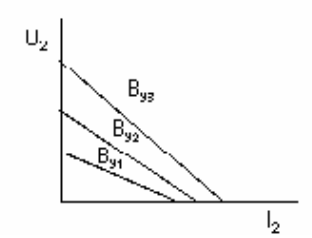 Здесь не учтена неравномерность распределения тока по сечению датчика. Выходное сопротивление, так же как и входное, с увеличением магнитного поля растет. На рис. 8 приведено семейство вольтамперных характеристик датчика для одного и того же значения входного тока и для нескольких значений индукции магнитного поля. Здесь не учтена неравномерность распределения тока по сечению датчика. Выходное сопротивление, так же как и входное, с увеличением магнитного поля растет. На рис. 8 приведено семейство вольтамперных характеристик датчика для одного и того же значения входного тока и для нескольких значений индукции магнитного поля.
Рисунок 8 - Семейство вольтамперных характеристик датчика Холла
С возрастанием поля крутизна возрастает вследствие того, что возрастает внутреннее сопротивление датчика R2. Одной из важных характеристик датчика, позволяющей оценить его эффективность, является коэффициент передачи К. Он определяется как отношение выходного напряжения к входному при заданном значении управляющего магнитного поля:
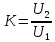 (21) (21)
Коэффициент передачи:
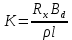 (22) (22)
Коэффициент передачи с увеличением индукции магнитного поля возрастает. Обычно датчик э.д.с. Холла работает на внешнюю нагрузку. Схема включения показана на рис. 7 (нижний рисунок). Подводимая к датчику мощность от внешнего источника тока равна:
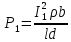 (23) (23)
Где RН — сопротивление нагрузки. Мощность, отдаваемая в нагрузку, при согласовании выходного сопротивления и нагрузки достигается максимальная мощность, отдаваемая в нагрузку. Максимальная отдаваемая мощность ограничивается предельно допустимой мощностью рассеяния на датчике. Ко-ффициент полезного действия датчика Холла определяется как отношение мощности, отдаваемой в нагрузку РН к мощности на его входе:
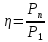 (24) (24)
К. п. д. датчика Холла обычно не превышает 20 %. Величина его не зависит от входного тока. Для увеличения э.д.с. Холла и выходной мощности необходима увеличивать входную мощность. Важной характеристикой датчика Холла является чувствительность γ. Определяется она как э. д. с., возникающая на холловских контактах при единичном управляющем токе и единичном значении магнитной индукции. Важным параметром датчика Холла является отношение, характеризующее э. д. с. Холла, приходящееся на единицу магнитной индукции. Этот параметр называется магнитной чувствительностью.
Конструкции и применение датчиков Холла. Для изготовления датчиков Холла необходимо добиваться следующих основных показателей:
а) Высокого значения Rx, когда необходимо получить высокое значение э. д. с. Холла в режиме холостого хода;
б) Высокой проводимости при заданном значении коэффициента Холла, когда датчик работает на внешнюю нагрузку, потребляющую ток, и часть э.д.с. Холла падает на внутреннем сопротивлении датчика между электродами Холла, обусловливая вредные потери;
в) Низкого температурного коэффициента, коэффициента Холла и проводимости.
Материал, из которого изготовляют датчик Холла, должен иметь максимальную подвижность носителей заряда с минимальными температурными зависимостями подвижности и концентраций носителей заряда.
Для получения наибольшего значения э. д. с. Холла необходимо выбирать материал с небольшой электропроводностью. Для этой цепи используют пленки селенида и теллурида ртути, антимонида индия и твердые растворы этих соединений. Они обладают высокой подвижностью носителей заряда даже в тонких монокристаллических пленках. Тонкопленочные датчики, полученные методом испарения из этих материалов, обладают слабой зависимостью коэффициента Холла и сопротивления от температуры и от напряженности магнитного поля, что определило их широкое применение, несмотря на сравнительно низкую э. д. с. Холла.
Для изготовления датчиков Холла применяют также монокристаллический германий и кремний, легированные мышьяком, фосфором и сурьмой. Датчики, изготовленные из этих материалов, имеют высокий коэффициент Холла и низ- кий температурный коэффициент (особенно кремниевые). Максимальная величина э.д.с. Холла достигает 1В.
Применяется для изготовления датчиков Холла антимонид индия, арсенид индия, а также сплав антимонида индия и ангимонида галлия. Датчики, изготовленные из этих материалов, имеют сильную зависимость сопротивления и коэффициента Холла от температуры и магнитного поля. Это ограничивает их применение.
Полупроводниковый слиток разрезается на пластины, которые посредством шлифовки доводятся до требуемой толщины. Далее пластины разрезают на прямоугольники нужных размеров, которые снабжают четырьмя омическими контактами. Два из них предназначены для подведения к датчику напряжения от внешнего источника. Они выполняются по всей ширине пластины, чтобы получить равномерное распределение входного тока по сечению пластины на всей ее длине. Два других электрода предназначены для регистрации э. д. с. Холла.
Эти контакты должны быть расположены строго в одном сечении, в противном случае между ними будет возникать разность потенциалов и при отсутствии магнитного поля за счет протекания тока.
Учитывая, что выходной ток очень мал, иногда выходные электроды выполняют точечными. Из теллурида и селенида ртути датчики Холла могут быть изготовлены также прессованием порошков при температуре около 500 К.
Пленочные датчики изготавливают посредством нанесения тонких пленок на подложку методом вакуумного испарения исходного материала.
Материалом подложки могут служить слюда, керамика или другие изоляционные материалы. Материал подложки должен обеспечить хорошую адгезию напыляемого материала и иметь с ним близкий температурный коэффициент линейного расширения. Контакты пленочных датчиков наносят испарением в вакууме. Для стабилизации параметров готовую пленку в течение нескольких часов подвергают термостарению при температуре 100° С. Пленочные датчики тоньше пластиночных. Их толщина определяется в основном подложкой. Преимуществом их является высокое сопротивление, что удобно при согласовании с нагрузкой.
 Получили развитие два новых прогрессивных метода изготовления датчиков Холла. Это метод диффузии, примеси я метод эпитаксиального выращивания. Оба эти метода широко применяют при изготовлении диодов и транзисторов. Посредством диффузии примеси на материале p-типа образуется p- n-переход. На диффузионном n-слое размещаются электроды, а p- n-переход служит изолирующим слоем (рис. 9). Получили развитие два новых прогрессивных метода изготовления датчиков Холла. Это метод диффузии, примеси я метод эпитаксиального выращивания. Оба эти метода широко применяют при изготовлении диодов и транзисторов. Посредством диффузии примеси на материале p-типа образуется p- n-переход. На диффузионном n-слое размещаются электроды, а p- n-переход служит изолирующим слоем (рис. 9).
Рисунок 9 - Диффузионный датчик Холла
 При эпитаксиальном выращивании подложкой может быть как монокристаллическая пластина того же материала, так и изоляционные материалы. Датчики Холла, полученные этими методами, имеют преимущества монокристаллических датчиков (высокий коэффициент Холла и хорошую стабильность) и преимущества пленочных (высокую чувствительность). Толщина рабочего слоя у них не более, чем у пленочных. Для защиты от механических и климатических воздействий изготовленный датчик покрывают синтетической смолой и приклеивают к изоляционной подложке или помещают в бронзовый корпус. Последний способствует отводу от датчика тепла. На рис. 10 приведено несколько конструктивных исполнений датчика Холла. На рис. 10, а показан датчик, выпускаемый без корпуса и подлежащий заливке компаундом после установки в воздушный зазор магнитопровода. На рис. 10, в приведен датчик с оболочкой из эпоксидной смолы. На рис. 10, б показан датчик, заключенный в ферритовую оболочку с симметричной магнитной системой. При эпитаксиальном выращивании подложкой может быть как монокристаллическая пластина того же материала, так и изоляционные материалы. Датчики Холла, полученные этими методами, имеют преимущества монокристаллических датчиков (высокий коэффициент Холла и хорошую стабильность) и преимущества пленочных (высокую чувствительность). Толщина рабочего слоя у них не более, чем у пленочных. Для защиты от механических и климатических воздействий изготовленный датчик покрывают синтетической смолой и приклеивают к изоляционной подложке или помещают в бронзовый корпус. Последний способствует отводу от датчика тепла. На рис. 10 приведено несколько конструктивных исполнений датчика Холла. На рис. 10, а показан датчик, выпускаемый без корпуса и подлежащий заливке компаундом после установки в воздушный зазор магнитопровода. На рис. 10, в приведен датчик с оболочкой из эпоксидной смолы. На рис. 10, б показан датчик, заключенный в ферритовую оболочку с симметричной магнитной системой.
Рисунок 10 - Конструкции датчиков Холла
Ферритовое основание 1 и крышка 4 имеют одинаковые размеры. Полупроводниковая пластина 6 наклеена прямо на ферритовое основание. Ферритовый стержень 3 концентрирует магнитный поток на поверхность датчика. Стенки 5 и 2 выполнены из немагнитного материала и обеспечивают необходимый зазор между ферритовым стержнем и полупроводниковой пластиной (обычно 2—3 мкм). На основе эффекта Холла можно создать ряд устройств и приборов, обладающих ценными и даже уникальными свой-ствами и занимающих важное место в измерительной технике, автоматике, радиотехнике и т. д.
Так как э. д. с. Холла пропорциональна току I и индукции магнитного поля, то при постоянной величине тока вели- чина э. д. с. будет пропорциональна только индукции магнитного поля. Это позволяет использовать датчики Холла для измерения индукции магнитных полей. Одним из приборов, в которых используется это свойство, является магнитометр, измеряющий как малые, так и большие поля (10 — 100 А/м).
Кроме того, датчики э. д. с. Холла применяют для измерения токов и мощностей. Если поддерживать постоянной напряженность магнитного поля, то э. д. с. Холла будет изменяться пропорционально величине тока, протекающего через датчик. Если датчик Холла поместить в магнитное поле, пропорциональное протекающему через нагрузку току, и на вход его подать напряжение, пропорциональное напряжению на нагрузке, то э. д. с. Холла будет пропорциональна мощности, выделяемой в нагрузке. Датчики Холла могут применяться для измерения силы, давлений, углов, перемещений и других неэлектрических величин. Если, например, датчик Холла перемещать в неоднородном магнитном поле, поддерживая входной ток постоянным, то э. д. с. Холла будет изменяться пропорционально напряженности магнитного поля, а следовательно, и местоположению датчика.
В полупроводниковом производстве эффект Холла используется для измерения подвижности и концентрации носителей полупроводникового материала. Для этой цели на специальном подготовленном образце измеряют э. д. с. Холла и по его величине судят о подвижности и концентрации носителей заряда материала, используемого для изготовления полупроводниковых приборов.
|
|
|
 Скачать 0.91 Mb.
Скачать 0.91 Mb. Эффект Холла в полупроводниках. Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлежности полупроводника к n- или p-типу, так как в полупроводниках n-типа знак носителей тока отрицательный, полупроводниках p-типа – положительный.
Эффект Холла в полупроводниках. Эффект Холла наблюдается не только в металлах, но и в полупроводниках, причем по знаку эффекта можно судить о принадлежности полупроводника к n- или p-типу, так как в полупроводниках n-типа знак носителей тока отрицательный, полупроводниках p-типа – положительный. 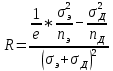 (13)
(13)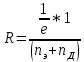 (14)
(14)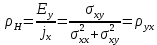 (15)
(15)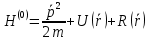 (16)
(16)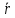 ) - периодический потенциал, создаваемый как обменным взаимодействием, так и кристаллической решеткой; R(
) - периодический потенциал, создаваемый как обменным взаимодействием, так и кристаллической решеткой; R(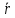 ) - потенциал рассеяния, связанный с любыми нарушениями периодичности (примеси, тепловые колебания токов, магнитные неоднородности). Если первый член гамильтониана характеризует действие силы Лоренца, то последующие свидетельствуют о том, что имеется АЭХ, пропорциональный магнитному моменту, и приводят к созданию асимметрии при рассеянии электронов проводимости, приводящей к холловскому закручиванию в отсутствии внешнего магнитного поля. Этим двум требованиям удовлетворяет спин-орбитальное взаимодействие. К возможным типам СОВ можно отнести собственное и несобственное. Собственное спин-орбитальное взаимодействие есть взаимодействие спина самого электрона с магнитным полем, которое создается при движении электрона по орбите. Несобственное СОВ является взаимодействием орбиты i-го электрона проводимости со спином другого j -го (локализованного или коллективизированного) электрона.
) - потенциал рассеяния, связанный с любыми нарушениями периодичности (примеси, тепловые колебания токов, магнитные неоднородности). Если первый член гамильтониана характеризует действие силы Лоренца, то последующие свидетельствуют о том, что имеется АЭХ, пропорциональный магнитному моменту, и приводят к созданию асимметрии при рассеянии электронов проводимости, приводящей к холловскому закручиванию в отсутствии внешнего магнитного поля. Этим двум требованиям удовлетворяет спин-орбитальное взаимодействие. К возможным типам СОВ можно отнести собственное и несобственное. Собственное спин-орбитальное взаимодействие есть взаимодействие спина самого электрона с магнитным полем, которое создается при движении электрона по орбите. Несобственное СОВ является взаимодействием орбиты i-го электрона проводимости со спином другого j -го (локализованного или коллективизированного) электрона. 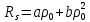 (17)
(17)
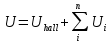 (18)
(18)
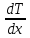 , причем носители, движущиеся от «горячего» токового электрода к «холодному», имеют большую энергию по сравнению с носителями, движущимися в обратном направлении;
, причем носители, движущиеся от «горячего» токового электрода к «холодному», имеют большую энергию по сравнению с носителями, движущимися в обратном направлении; 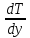 в скрещенном магнитном поле Bz ;
в скрещенном магнитном поле Bz ; 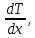 особенно в высокопроводящих образцах, когда Uσ мала.
особенно в высокопроводящих образцах, когда Uσ мала.
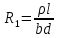 (19)
(19)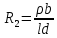 (20)
(20)
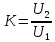 (21)
(21)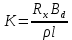 (22)
(22)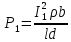 (23)
(23)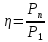 (24)
(24)
