Курсовая. Курсовая работа по дисциплине Физические основы получения информации
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
1011 (м3/кулон). Коэффициент Холла R может быть выражен через подвижность носителей заряда Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Магнитогорский государственный технический университет им. Г.И. Носова» (ФГБОУ ВО «МГТУ им. Г.И. Носова») Кафедра Физики КУРСОВАЯ РАБОТА по дисциплине: ___________Физические основы получения информации__________ на тему: __Измерительный преобразователь на основе эффекта Холла для измерения индукции магнитного поля__________________________________________________ Исполнитель: Ефремов Александр Юрьевич студент 2 курса, группы ТПРп-18-1 Руководитель: Дубский Геннадий Алексеевич, доцент, к.ф.-м.н. Работа допущена к защите "_____" _________ 20__г. __________________ (подпись) Работа защищена "_____" _________ 20__г. с оценкой __________________________ (оценка) (подпись) Магнитогорск, 2020 Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Магнитогорский государственный технический университет им. Г.И. Носова» (ФГБОУ ВО «МГТУ им. Г.И. Носова») Кафедра Физики ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Тема: _Измерительный преобразователь на основе эффекта_ _____Холла для измерения индукции магнитного поля_____ Студенту: ___________________________________________ Исходные данные: _____________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ ____________________________________________________________________________ Срок сдачи: «______» _______________ 20__г. Руководитель: ______________________ /____________________________/ (подпись) (расшифровка подписи) Задание получил: ___________________ /____________________________/ (подпись) (расшифровка подписи) Магнитогорск, 2020 СОДЕРЖАНИЕ Введение………………………………………………………………………………………….4 Измерительные преобразователи…………………………………………………………...5 1.1. Индукционное измерительное преобразование……………………………………….5 1.2. Гальваномагнитное измерительное преобразование…………………………………6 1.3. Измерение магнитной индукции гальваномагнитными преобразователями……….6 1.4. Измерение напряженности магнитного поля………………………………………….7 Намагничивающие устройства……………………………………………………………...8 Эффект Холла………………………………………………………………………………..9 3.1. Теоретические сведения по эффекту Холла…………………………………………..9 3.2. Эффект Холла в различных средах…………………………………………………...10 3.3. Побочные явления эффекта Холла…………………………………………………...13 3.4. Датчики Холла…………………………………………………………………………14 3.5. Измерение ЭДС Холла………………………………………………………………...19 Магнитное поле катушек Гельмгольца…………………………………………………...19 Измерение магнитного поля соленоидов…………………………………………………20 Заключение……………………………………………………………………………………...24 Библиографический список……………………………………………………………………25 ВВЕДЕНИЕ Из электростатики известно, что если проводник поместить во внешнее электростатическое поле, то на поверхности проводника возникнут индуцированные электрические заряды, а напряженность электрического поля в проводнике будет равна нулю. Если при этом через проводник пропускать электрический ток, то движение зарядов в проводнике будет совершенно аналогичным, как в присутствии внешнего электрического поля, так и в его отсутствии. Но, если при этом, приложить магнитное поле, то на соответствующих гранях образца будут накапливаться заряды из-за взаимодействия электрического тока через проводник и приложенного магнитного поля. То есть возникнет эффект Холла. Причем, можно подобрать такие магнитные поля и токи, которые позволят скомпенсировать индуцированный внешним электростатическим полем заряд на проводнике. Таким образом, есть принципиальная возможность построения датчика электростатического поля основанного на эффекте Холла. Конечно, предлагаемый способ требует еще тщательного изучения и проверки. В качестве предлагаемого для такого датчика материала проводника выберем медь. Это продиктовано тем, что медь обладает высокой электропроводностью и доступностью. В конце прошлого века молодой американский студент-физик Эдвин Холл сделал открытие, вписавшее его имя в учебники физики. Он проводил простой, "студенческий" опыт - изучал распространение тока в тонкой металлической пластинке, помещенной между полюсами сильного электромагнита. Студенты всех университетов проходят лабораторную практику, где на простых примерах их обучают мастерству эксперимента. Так было и в этот раз. Скромный студент и предполагать не мог, что его простенький опыт породит целую лавину исследований, часть которых будет отмечена самой почетной научной наградой - Нобелевской премией. Прибор, с которым работал Холл, состоял из двух крест-накрест расположенных электрических цепей - так перевязывают ленточкой коробки с конфетами. Цепи различались тем, что одна из них содержала электрическую батарею, и ток от нее проходил вдоль пластинки, другая, поперечная, не имела источников тока и просто соединяла края пластины. Как и следовало ожидать, в случае, когда электромагнит был выключен, приборы фиксировали течение тока лишь вдоль пластины - в цепи с батареей - и его отсутствие в "пустой" поперечной цепи. Ничего удивительного. Однако, как только включался электромагнит, в поперечной цепи как бы из ничего, сам по себе возникал электрический ток. Это было интересно, но никакого чуда тут не было - объяснение нашлось довольно быстро. На движущиеся в продольной цепи электроны действует хорошо известная еще из школьного учебника сила Лоренца, отклоняющая электроны в поперечном направлении, что и порождало небольшой ток в поперечной цепи - все элементарно просто. Более полувека, полузабытое, это явление оставалось в тылу физической науки. Откопали его в архивах специалисты по микроэлектронике. Сначала выяснилось, что если грубые измерительные приборы времен Холла заменить на современные, то открытое им явление можно использовать для подсчета числа заряженных частиц, движение которых порождает электрический ток, а это очень важно для конструкторов малошумящих транзисторов и других высокочувствительных микроэлектронных устройств, работающих с очень слабыми токами и магнитными полями. 1 Измерительные преобразователи Измерительные преобразования в магнитных полях основаны на физических эффектах, результатом которых является преобразование в электрический сигнал характеристик магнитных полей или магнитных характеристик материалов и изделий. Обычно при данном виде измерительных преобразований объект измерения или его часть помещается в постоянное или переменное магнитное поле, создаваемое за счет протекания электрического тока по проводнику, обмотке или непосредственно по объекту, а также постоянными магнитами. 1.1 Индукционное измерительное преобразование Индукционное измерительное преобразование основано на явлении электромагнитной индукции, суть которого заключается в возникновении в замкнутом проводящем контуре, пронизываемом изменяющимся во времени магнитным потоком Φ, ЭДС индукции e: 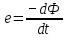 (1) (1)Электрический ток, вызываемый этой ЭДС, называется индукционным. Электромагнитная индукция открыта английским ученым М. Фарадеем в 1831 г. и независимо американским ученым Дж. Генри в 1832 г. Согласно (1) ЭДС индукции прямо пропорциональна скорости изменения магнитного потока. Знак минус в правой части выражения определяет направление индукционного тока в соответствии с правилом Ленца, согласно которому индукционный ток в контуре направлен так, что создаваемый им магнитный поток стремится препятствовать тому изменению магнитного потока, которое вызывает данный ток (следствие закона сохранения энергии). Для обмотки, имеющей w витков, вводится понятие потокосцепления Ψ=wΦ. Соответственно эдс индукции для обмотки: 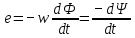 (2) (2)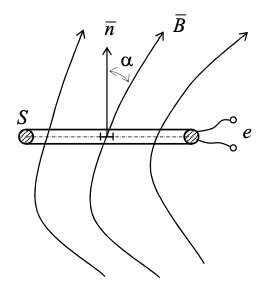 В общем случае магнитный поток Φ определяется интегрированием скалярного произведения векторов магнитной индукции В общем случае магнитный поток Φ определяется интегрированием скалярного произведения векторов магнитной индукции 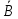 и площади элементарной площадки d и площади элементарной площадки d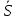 по площади поверхности S, ограниченной контуром среднего витка. Направление вектора элементарной площадки d по площади поверхности S, ограниченной контуром среднего витка. Направление вектора элементарной площадки d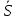 совпадает с нормалью совпадает с нормалью 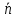 к этой площадке (рис. 1). к этой площадке (рис. 1). Рисунок 1 - Индукционная обмотка в неоднородном магнитном поле ЭДС индукции в случае гармонического магнитного поля изменяется по гармоническому закону. Амплитуда ЭДС равна произведению wScosαBmω, а фаза ЭДС отстает от фазы индукции на угол 90°. Зависимость амплитуды ЭДС индукции от параметров гармонического магнитного поля (амплитуды индукции, частоты, ориентации силовых линий относительно обмотки) и фазы ЭДС от фазы индукции магнитного поля позволяет на основе измерения ЭДС получать измерительную информацию об этих параметрах. Если поместить индукционную обмотку в постоянное магнитное поле, то при отсутствии движения обмотки не будет изменения магнитного потока через обмотку (скорость изменения магнитного потока равна нулю) и соответственно ЭДС индукции в этом случае тоже будет равна нулю. 1.2 Гальваномагнитное измерительное преобразование Гальваномагнитное измерительное преобразование основано на использовании гальваномагнитных явлений, связанных с действием магнитного поля на электрические (гальванические) свойства проводников и полупроводников, по которым протекает электрический ток. Наибольшее значение имеют поперечные гальваномагнитные явления, когда силовые линии магнитного поля перпендикулярны направлению электрического тока. К ним относятся эффект Холла и магниторезистивный эффект (эффект Гаусса). Эффект Холла заключается в возникновении в твердом проводнике с током, помещенным в поперечное магнитное поле, электрического поля, перпендикулярного направлениям тока и магнитного поля. 1.3 Измерение магнитной индукции гальваномагнитными преобразователями Преобразователи Холла выполнены в виде плоской прямоугольной пластины из полупроводникового материала с размерами a b и толщиной d . На коротких поперечных гранях пластина имеет два сплошных электрода, которые называются токовыми (управляющими или входными электродами) и через которые пропускают ток I питания преобразователя. Два других электрода (как правило, точечные), располагаются посередине продольных (широких) граней пластины и называются холловскими или выходными электродами. При пропускании тока I через токовые электроды в магнитном поле B, направленном перпендикулярно плоскости преобразователя, между выходными электродами возникает ЭДС Холла EX , которая описывается выражением вида: 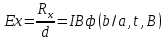 (3) (3)Где Rx - постоянная Холла, d - толщина пластины; b − длина пластины; (b / a,t, B) − поправочный коэффициент формы, в общем случае зависящий от размеров преобразователя (его формы), размеров выходных электродов, индукции измеряемого магнитного поля и т.д. Для преобразователей Холла конкретных размеров при постоянной температуре и при малых магнитных полях (десятые доли теслы) справедливо выражение: EX XIB (4) Где коэффициент X называется чувствительностью. При измерении магнитных полей управляющий ток I остается неизменным. В этом случае водят понятие магнитной чувствительности при определенном, чаще всего номинальном, управляющем токе I0. Магнитная чувствительность и номинальный ток приводятся в паспорте преобразователя Холла. В зависимости от материала пластины и конструкции преобразователя значение магнитной чувствительности изменяется от 0,06 до 0,6 В/Тл. 1.4 Измерение напряженности магнитного поля 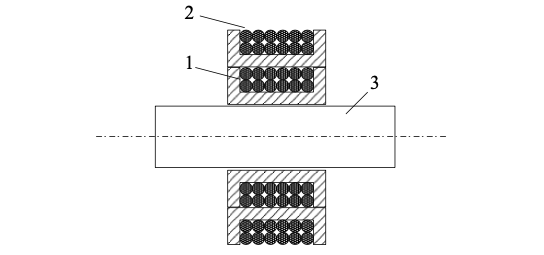 Измерение для индукционных преобразователей показаны на рис. 2. Первичный измерительный преобразователь напряженности магнитного поля состоит из катушек 1 и 2, нанесенных на соответствующие каркасы и включенных встречно, и ферримагнитного материала 3. Измерение для индукционных преобразователей показаны на рис. 2. Первичный измерительный преобразователь напряженности магнитного поля состоит из катушек 1 и 2, нанесенных на соответствующие каркасы и включенных встречно, и ферримагнитного материала 3. Рисунок 2 - Конструкция ПИП напряженности магнитного поля Выходной сигнал ПИП выражается формулой: 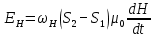 (5) (5)Где 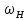 - число витков ПИП напряженности магнитного поля обмоток 1 и 2; (S2 - S1) - площадь, заключенная между этими катушками. - число витков ПИП напряженности магнитного поля обмоток 1 и 2; (S2 - S1) - площадь, заключенная между этими катушками.Гальваномагнитные преобразователи находят широкое применение для измерения напряженности магнитного поля у поверхности ферримагнитных тел. При этом преобразователь Холла должен иметь малые размеры и достаточную чувствительность: 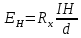 (6) (6)Где Rx - постоянная Холла; I - ток питания; d - толщина пластины, см; H - напряженность магнитного поля, А/см. Тангенциальная составляющая напряженности магнитного поля на границе ферромагнитного материала и воздуха равны. Если к исследуемой ферромагнитной пластине П перпендикулярно приложить датчик Холла Х с возможно малыми размерами (рис. 3), то измеряя тангенциальную составляющую напряженности магнитного поля в воздухе рядом с поверхностью исследуемого тела, измеряем тангенциальную 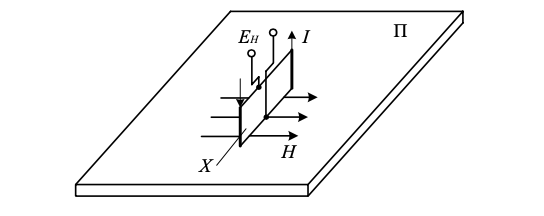 составляющую напряженности поля внутри этого тела. составляющую напряженности поля внутри этого тела. Рисунок 3 - Измерение тангенциальной составляющей напряженности магнитного поля Метод, основанный на влиянии магнитного поля на характеристики ферромагнитных материалов, реализуется в магниторезистивных и ферромодуляционных преобразователях. 2 Намагничивающие устройства При измерении магнитных характеристик изделий из ферромагнитных материалов, их необходимо помещать во внешнее магнитное поле, создаваемое с помощью устройства намагничивания, в обмотки которого подается электрический ток требуемой формы. Напряженность магнитного поля, созданную при помощи соленоида, можно определить по току, протекающему в соленоиде. Для соленоида напряженность определяется выражением: 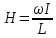 (7) (7)Где − число витков соленоида; I − намагничивающий ток протекающий по соленоиду; L − длина соленоида. Приведенная формула дает достаточно хорошие результаты для длинных катушек небольшого диаметра. При использовании в качестве намагничивающей системы катушки Гельмгольца, зависимость напряженности магнитного поля от тока выглядит следующим образом: 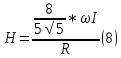 Где R − радиус катушки, м; − число витков на одной половине (на одном кольце); I − ток в обмотке, А. Для определения магнитных свойств ферромагнитных материалов также применяют пермеаметры различных конструкций. Помимо создания замкнутой магнитной цепи, что облегчает процесс намагничивания, при измерениях в пермеаметре уменьшается погрешность определения напряженности поля для образца разомкнутой формы. 3 Эффект Холла 3.1 Теоретические сведения по эффекту Холла Эффектом Холла называется появление в проводящем образце с током плотностью j, помещенном в магнитное поле B, электрического поля Ех, перпендикулярного B и j (рис.4). При этом напряженность электрического поля, называемого еще полем Холла, равна: 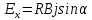 (9) (9)Где угол между векторами B и j ( <180°). Когда B j, то величина поля Холла Ех максимальна: Ex=RBj. Величина R, называемая коэффициентом Холла, является основной характеристикой эффекта Холла. Как правило, исследуемый проводящий образец имеет форму пластинки длиной l, шириной b и толщиной d. Сила тока через проводник связана с плотностью тока соотношением: 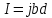 (10) (10)Магнитное поле прикладывается перпендикулярно плоскости пластинки. На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется ЭДС Холла Vx: 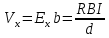 (11) (11)Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Холла эффект относится к нечетным гальваномагнитным явлениям. 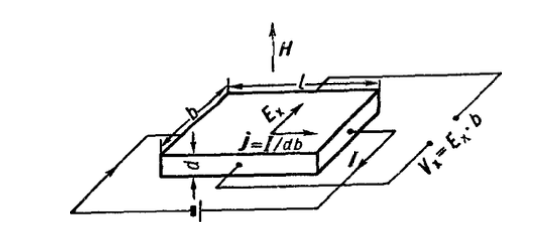 Рисунок 4 - Измерение ЭДС Холла на пластине, помещенной в магнитное поле Простейшая теория Холла эффекта объясняет появление ЭДС Холла взаимодействием носителей тока (электронов проводимости и дырок) с магнитным полем. Под действием электрического поля носители заряда приобретают направленное движение (дрейф), средняя скорость которого (дрейфовая скорость) vдр 0. Плотность тока в проводнике, где n — концентрация числа носителей, е — их заряд. При наложении магнитного поля на носители действует Лоренца сила: F=e[Bvдр] под действием которой частицы отклоняются в направлении, перпендикулярном vдр и B. В результате в обеих гранях проводника конечных размеров происходит накопление заряда и возникает электростатическое поле — поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. В условиях равновесия 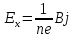 , отсюда , отсюда 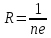 (м3/кулон). Знак R совпадает со знаком носителей тока. Для металлов, у которых концентрация носителей (электронов проводимости) близка к плотности атомов (n 1028 м), R (м3/кулон). Знак R совпадает со знаком носителей тока. Для металлов, у которых концентрация носителей (электронов проводимости) близка к плотности атомов (n 1028 м), R |

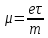 и удельную электропроводимость
и удельную электропроводимость 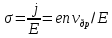 :
: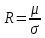 (12)
(12)