|
|
Курсовая работа по информатике. Курсовая работа. Курсовая работа по дисциплине Информатика (наименование учебной дисциплины согласно учебному плану)
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра информатики и ИКТ
КУРСОВАЯ РАБОТА
По дисциплине Информатика
(наименование учебной дисциплины согласно учебному плану)
Тема работы: Определение оптимальных сроков замены оборудования
Выполнил: студент гр. МНМ-20 Фёдорова А.В.
(шифр группы) (подпись) (Ф.И.О.)
Оценка:
Дата:
Проверил
руководитель работы: доцент Сарапулова Т.В.
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2021
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
УТВЕРЖДАЮ
Заведующий кафедрой
Маховиков А.Б.
(подпись)
«»2021 г.
Кафедра информатики и компьютерных технологий
КУРСОВАЯ РАБОТА
По дисциплине Информатика
(наименование учебной дисциплины согласно учебному плану)
ЗАДАНИЕ
студенту группы МНМ-20 Фёдорова А.В.
(шифр группы) (Ф.И.О.)
Тема работы: Определение оптимальных сроков замены оборудования средствами табличного процессора MSExcel, пакета математических расчетов MathCAD и с помощью VBA
Исходные данные к работе: Вариант №17. Разработать оптимальную стратегию замены оборудования возраста t лет в плановом периоде продолжительностью 14,9 лет, если известны: возраст оборудования на начало моделирования составляет 1,5 лет; стоимость продукции 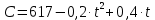 , производимой в течение года на оборудовании возраста t лет C(t); ежегодные расходы , производимой в течение года на оборудовании возраста t лет C(t); ежегодные расходы 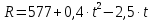 , связанные с эксплуатацией оборудования возраста t лет R(t). , связанные с эксплуатацией оборудования возраста t лет R(t).
Содержание пояснительной записки: Титульный лист, аннотация, содержание, введение, теоретические сведения для выполнения работы, расчетные формулы, решение с помощью таблиц Microsoft Excel, решение с использованием пакета MathCAD, решение в среде программирования VBA, выводы, библиографический список, приложение
Перечень графического материала: Рисунки, таблицы, формулы.
Срок сдачи законченной работы 9 апреля 20 21 г.
Задание выдал (руководитель работы) Сарапулова Т.В.
(подпись) (Ф.И.О.)
Задание принял к исполнению студент Фёдорова А.В.
(подпись) (Ф.И.О.)
Дата получения задания 18 февраля 20 21 г
Аннотация
В работе выполнен расчёт оптимальных сроков замены оборудования, в соответствии с начальным возрастом оборудования 1,5 лет и сроком моделирования 14,9 лет. Для решения задачи были использованы методы хорд и дихотомии, графические расчёты. Для получения численных значений искомых величин проведён расчёт и построены эпюры исследуемых величин средствами табличного процессора Microsoft Excel, математического пакета MathCAD, а также составлена программа в среде программирования VBA.
Работа содержит 33 страниц, 33 рисунка.
The summary
In this paper, the optimal timing of equipment replacement is calculated, in accordance with the initial age of the equipment of 1,5 years and the modeling period of 14,9 years. To solve the problem, we used chord and dichotomy methods, as well as graphical calculations. To obtain the numerical values of the desired quantities, the calculation was carried out and plots of the studied quantities were constructed using the Microsoft Excel table processor, the MathCAD mathematical package, and a program was compiled in the VBA programming environment.
The work contains 33 pages, 33 drawings.
Содержание
Введение 5
1 Реализация математической модели в среде MathCad 7
1.1 Решение задачи об определении оптимальных сроков замены оборудования в MathCad встроенными функциями 7
1.2 Решение задачи об определении оптимальных сроков замены оборудования в MathCad методом хорд 9
1.3 Решение задачи об определении оптимальных сроков замены оборудования в MathCad методом дихотомии 10
2 Решение задачи об определении оптимальных сроков замены оборудования в MS Excel 12
2.1 Графическое решение задачи об определении оптимальных сроков замены оборудования в MS Excel 12
2.2 Решение задачи об определении оптимальных сроков замены оборудования в MS Excel методом хорд 16
2.3 Решение задачи об определении оптимальных сроков замены оборудования в MS Excel методом дихотомии 16
2.4 Решение задачи об определении оптимальных сроков замены оборудования с помощью надстройки «Поиск решения» 18
3 Решение задачи об определении оптимальных сроков замены оборудования средствами Visual Basic For Applications 20
Заключение 28
Список использованной литературы 29
Приложение 1. Листинг кода 30
Введение
В период эксплуатации и хранения оборудование подвергается физическому и моральному износу. Физический износ характеризуется утратой оборудованием своих первоначальных качеств. Физический износ оборудования является причиной увеличения доли бракованных изделий, увеличения времени простоя оборудования по техническим причинам, перерасхода основных и вспомогательных материалов, простоев в связи с авариями, что в конечном итоге ведет к росту себестоимости продукции. Моральный износ оборудования бывает двух форм. Первая форма морального износа вызывает уменьшение стоимости оборудования вследствие удешевления их воспроизводства. Вторая форма морального износа наступает в том случае, если изменяется конструкция и эксплуатационные показатели новых машин, когда машина технически устарела и заменяется более совершенной.
Актуальной является задача разработка оптимальной стратегии замены оборудования. Важными величинами которой являются возраст оборудования на начало моделирования, стоимость самой продукции и ежегодные расходы. Изменение этих величин удобнее всего представить графически, для чего используются графики, называемые эпюрами. Для построения эпюр используют различные методы: хорд, дихотомии пр.
Компьютерные программы (табличный процессор Microsoft Excel, математический пакет MathCAD, среда программирования VBA и др.) будут использованы в качестве инструментов для получения необходимых нам вычислений и построения графиков, с помощью которых будет наглядно видно, как изменяются те или иные параметры.
Целью выполняемой работы является расчет оптимальных сроков замены оборудования. Разработать оптимальную стратегию замены оборудования возраста t лет в плановом периоде продолжительностью 14,9 лет, если известны: возраст оборудования на начало моделирования составляет 1,5 лет; стоимость продукции 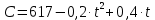 производимой в течение года на оборудовании возраста t лет C(t); ежегодные расходы производимой в течение года на оборудовании возраста t лет C(t); ежегодные расходы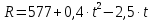 , связанные с эксплуатацией оборудования возраста t лет R(t). , связанные с эксплуатацией оборудования возраста t лет R(t).
1 Реализация математической модели в среде MathCad 1.1 Решение задачи об определении оптимальных сроков замены оборудования в MathCad встроенными функциями
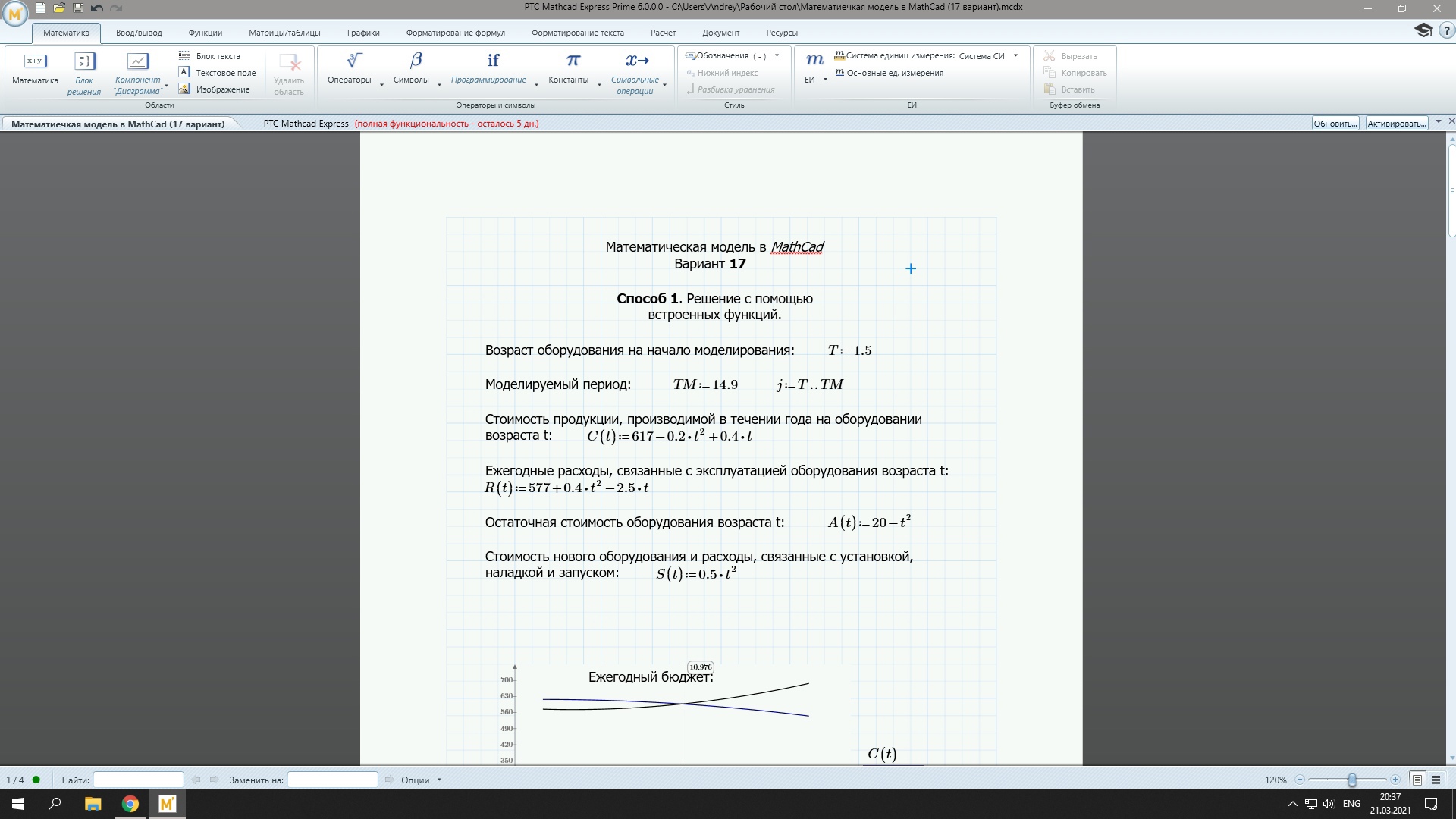
Рис 1. Ввод исходных данных в MathCad
Построим графики функций стоимости продукции, производимой ежегодно и ежегодных расходов, связанных с эксплуатацией оборудования в течение моделируемого периода, в одних координатах (рис.2).
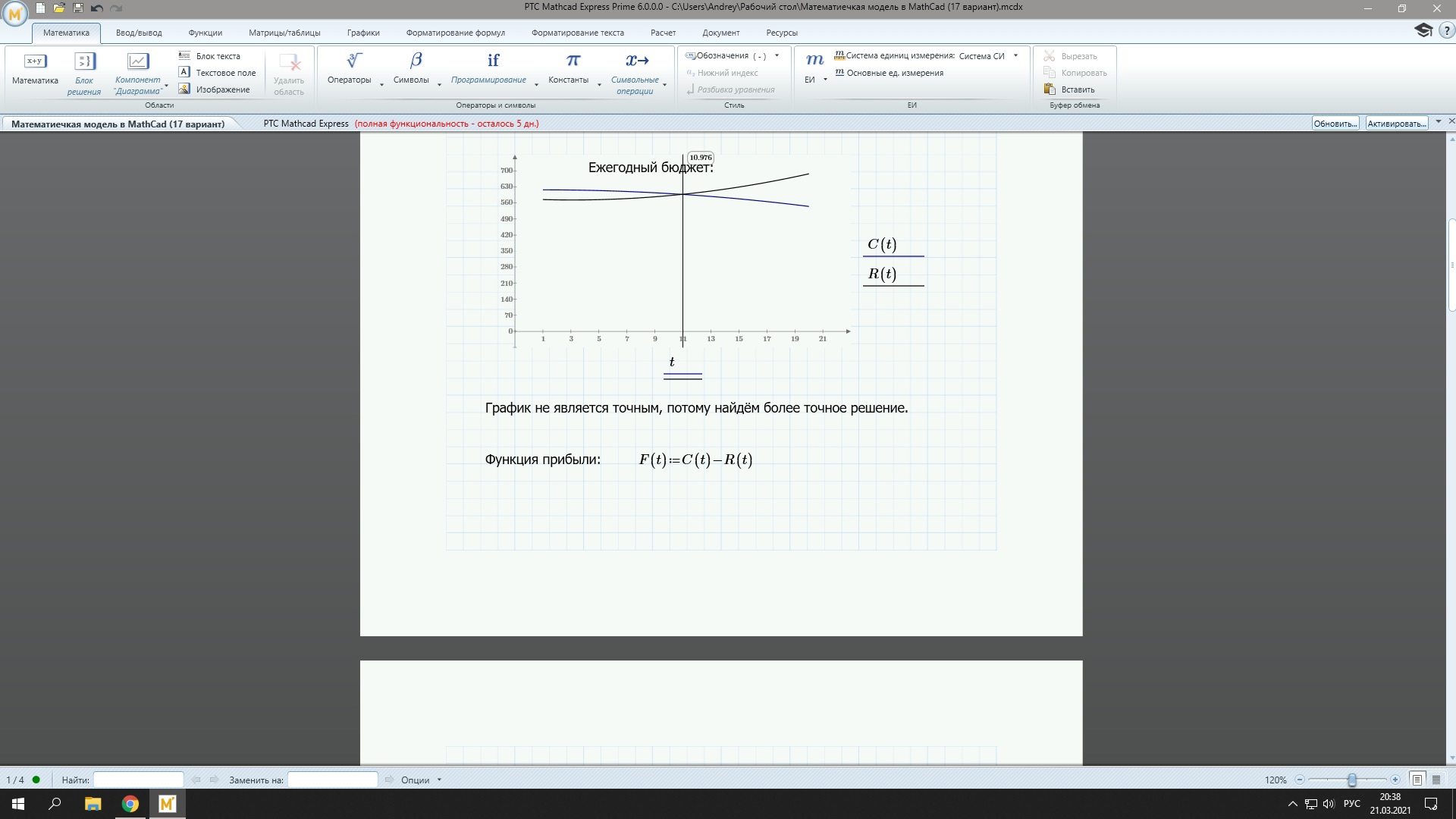
Рис.2. Изменение стоимости продукции и расходов на эксплуатацию оборудования в моделируемом периоде
На рисунке заметен момент времени, когда расходы сравняются с доходами, а затем и превысят их. Судя по графику, этот момент времени наступит примерно через 10,3 года после начала моделирования.
Графический способ сам по себе недостаточно точный. В большинстве случаев необходимо найти более точное решение. Сначала составим уравнение, отражающее цель нашей задачи:
𝐹(𝑡) = 𝐶(𝑡) − 𝑅(𝑡) (1)
Назовем ее функцией прибыли. Интересующая нас точка находится на пересечении новой функции F(t) с осью t. Именно в этой точке доходы сравняются с расходами (рис.3).
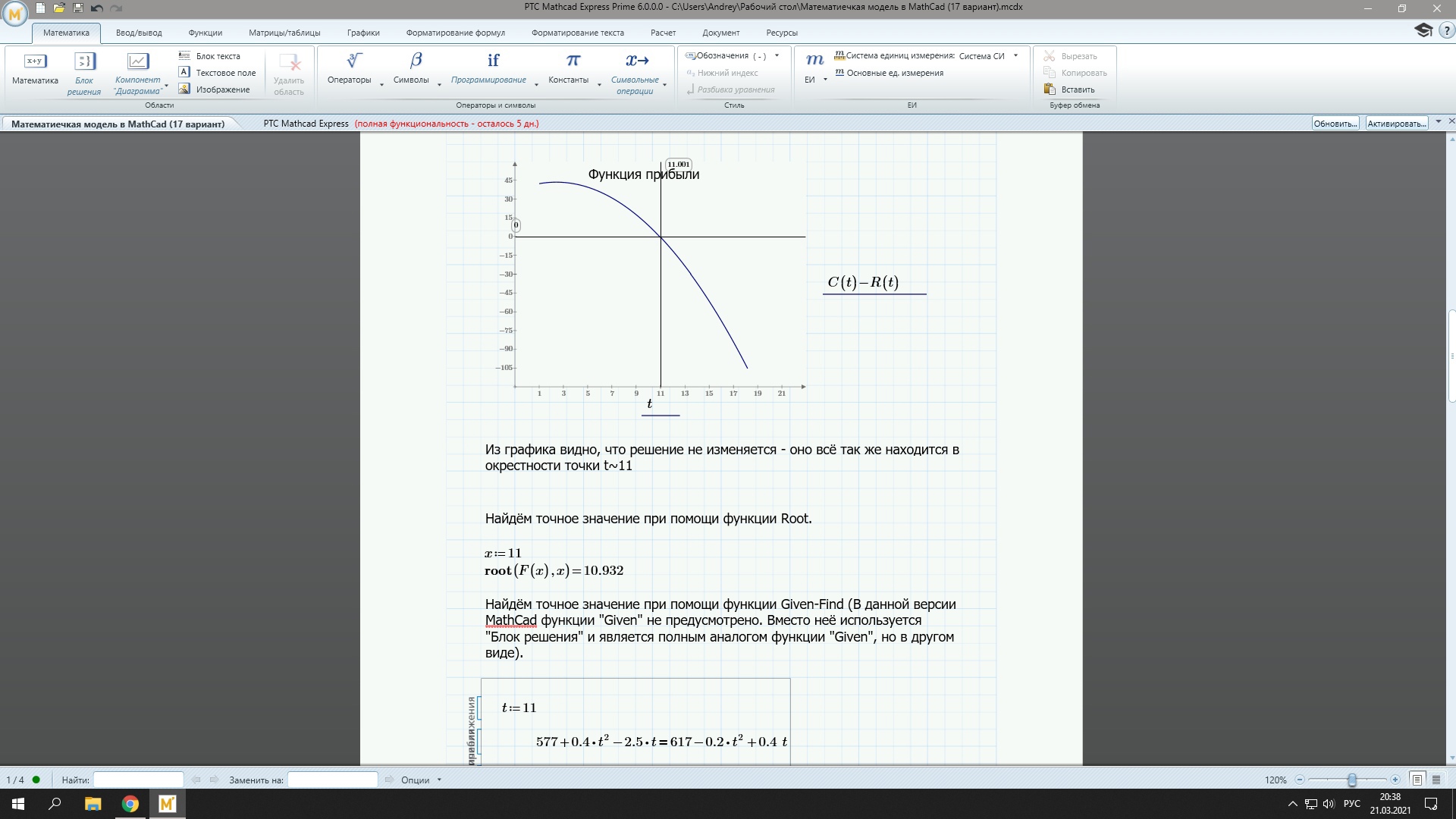
Рис.3. Функция прибыли, зависящая от срока эксплуатации оборудования
Из графика следует, что решение не изменится: его следует искать в окрестности точки t10,3. Уточним корень с помощью функции Root (рис. 4).

Рис.4. Решение задачи при помощи встроенной функции root
Для нахождения корней алгебраического уравнения воспользуемся встроенной функцией Polyroots. Ее достоинство заключается в том, что не требуется задавать приближенные к корню значения.
Также решим уравнение при помощи функции Given – Find. Она позволяет решать нелинейные уравнения, а также системы линейных и нелинейных уравнений. Для решения необходимо задать начальное приближение, достаточно близкое к точному решению. Затем следует ключевое слово given, указывающее, что далее последует уравнение или система уравнений. Завершает конструкцию ключевое слово find с аргументами в виде перечня переменных, значения которых нужно найти. В данном случае – одна переменная t. После знака равенства должно появиться решение уравнения (рис.5):
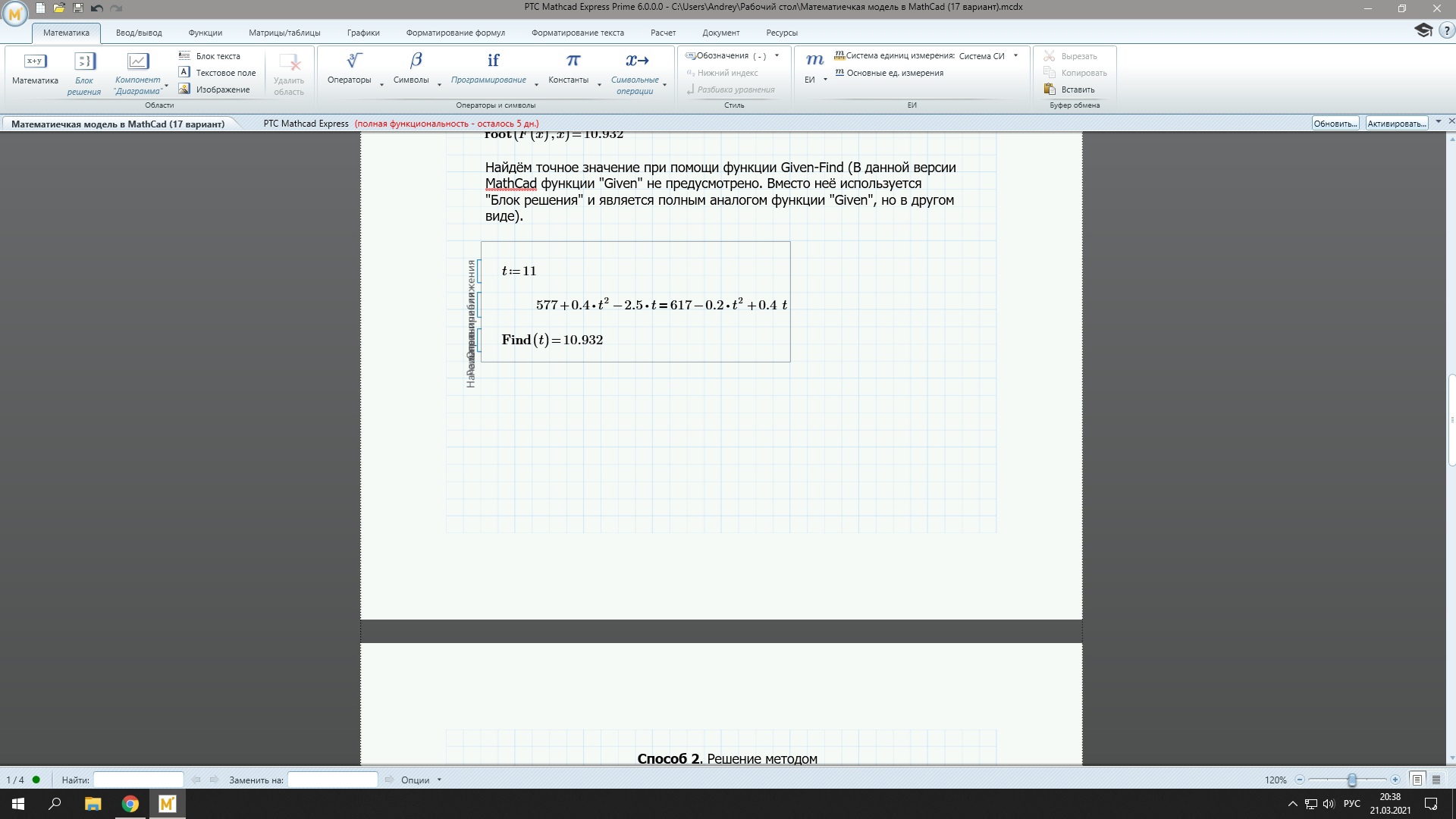
Рис.5. Решение задачи при помощи встроенной функции given – find
1.2 Решение задачи об определении оптимальных сроков замены оборудования в MathCad методом хорд
Суть метода хорд заключается в последовательном выполнении однотипных действий (итераций). Оба конца функции на интервале, Х – Х0, содержащем корень, соединяется хордой (рис. 6).
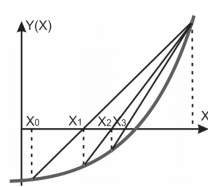
Рис.6. Графическая интерпретация метода хорд
Из подобных треугольников находится точка пересечения хорды с осью Х.
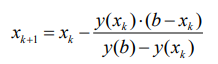 (2) (2)
Таким образом, найдена новая (по рисунку – левая граница интервала X1). Второй конец интервала (на рисунке – правый) со значением Х – неподвижный. Вновь концы функции на интервале Х - X1 соединяются хордой и итерация повторяется. Итерационный процесс завершается, когда погрешность будет меньше заданной. Погрешность в методе хорд рассчитывается по формуле:
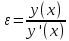 (3) (3)
Реализация метода хорд в MathCAD представлена на рисунке 7:
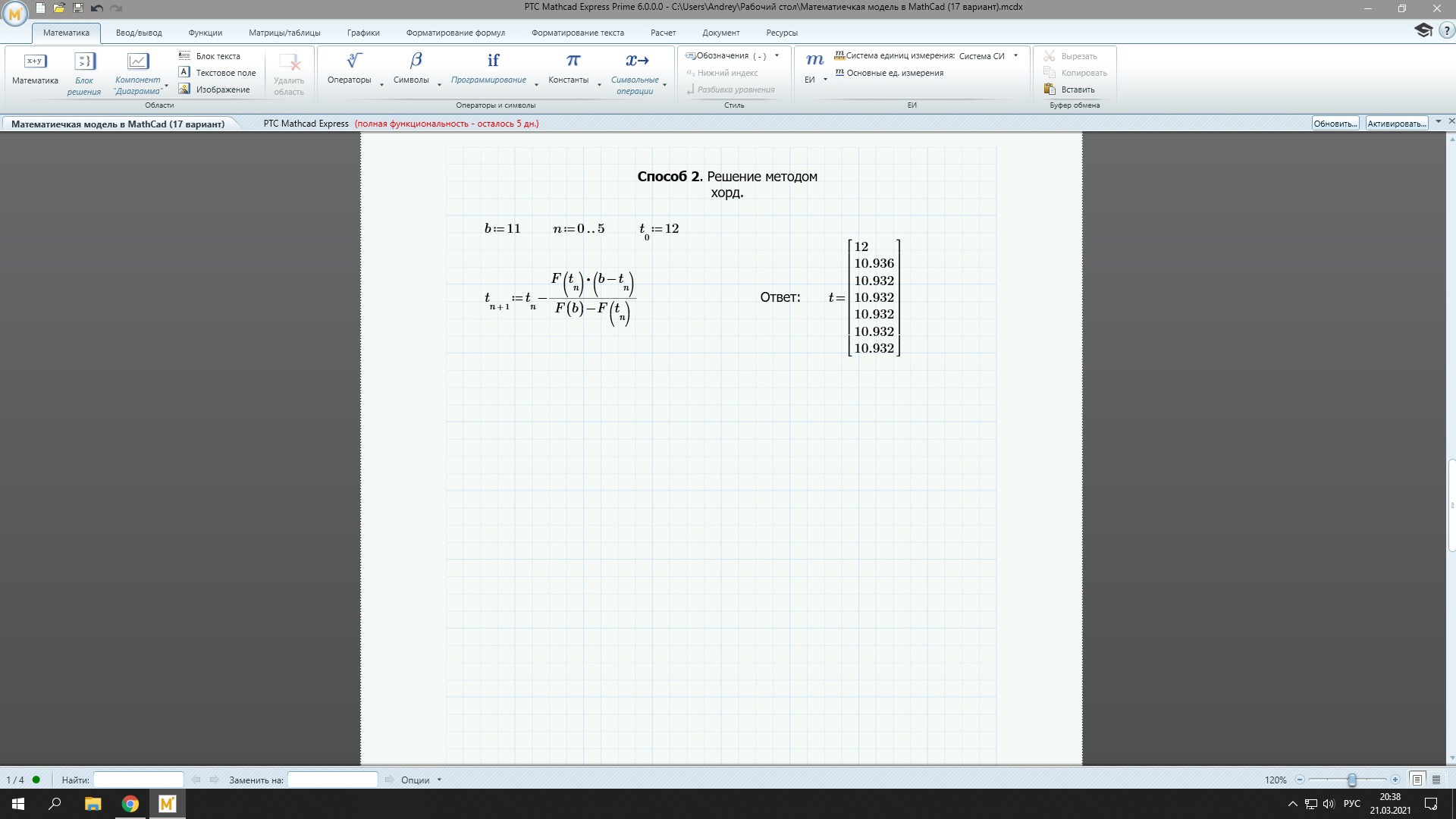
Рис.7. Решение задачи методом хорд
1.3 Решение задачи об определении оптимальных сроков замены оборудования в MathCad методом дихотомии
Метод дихотомии иначе называется методом деления отрезка пополам. Это тоже итерационный метод. Суть его следует из названия. Исходный отрезок, содержащий единственный корень, делится пополам. Далее сравниваются значение функции на середине отрезка со значениями функции на краях интервала. Очевидно, если знаки функции в середине отрезка и на одном из его краев совпадают, то корня (пересечения оси Х) там нет. Значит, можно сократить интервал в два раза, если перенести Х с того конца, где корня нет, на середину. Далее процесс повторяется до тех пор, пока длина интервала не окажется меньше заданной погрешности (рис.8).
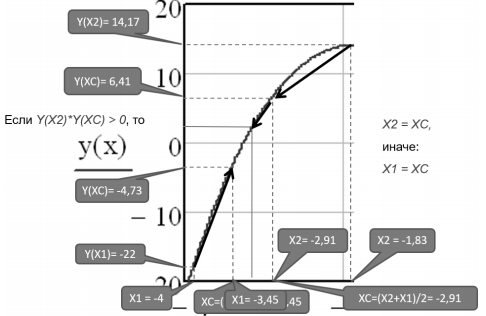
Рис.8. Графическая интерпретация метода дихотомии
В MathCAD этот метод значительно проще реализовать в виде программы (рис. 9):

Рис.9. Программа реализации метода хорд для решения задачи
Программа универсальна, осталось подставить функцию прибыли (на рисунке 10 она отсутствует), границы интервала и заданную погрешность. Результаты сходятся к значениям, полученным предыдущими способами.
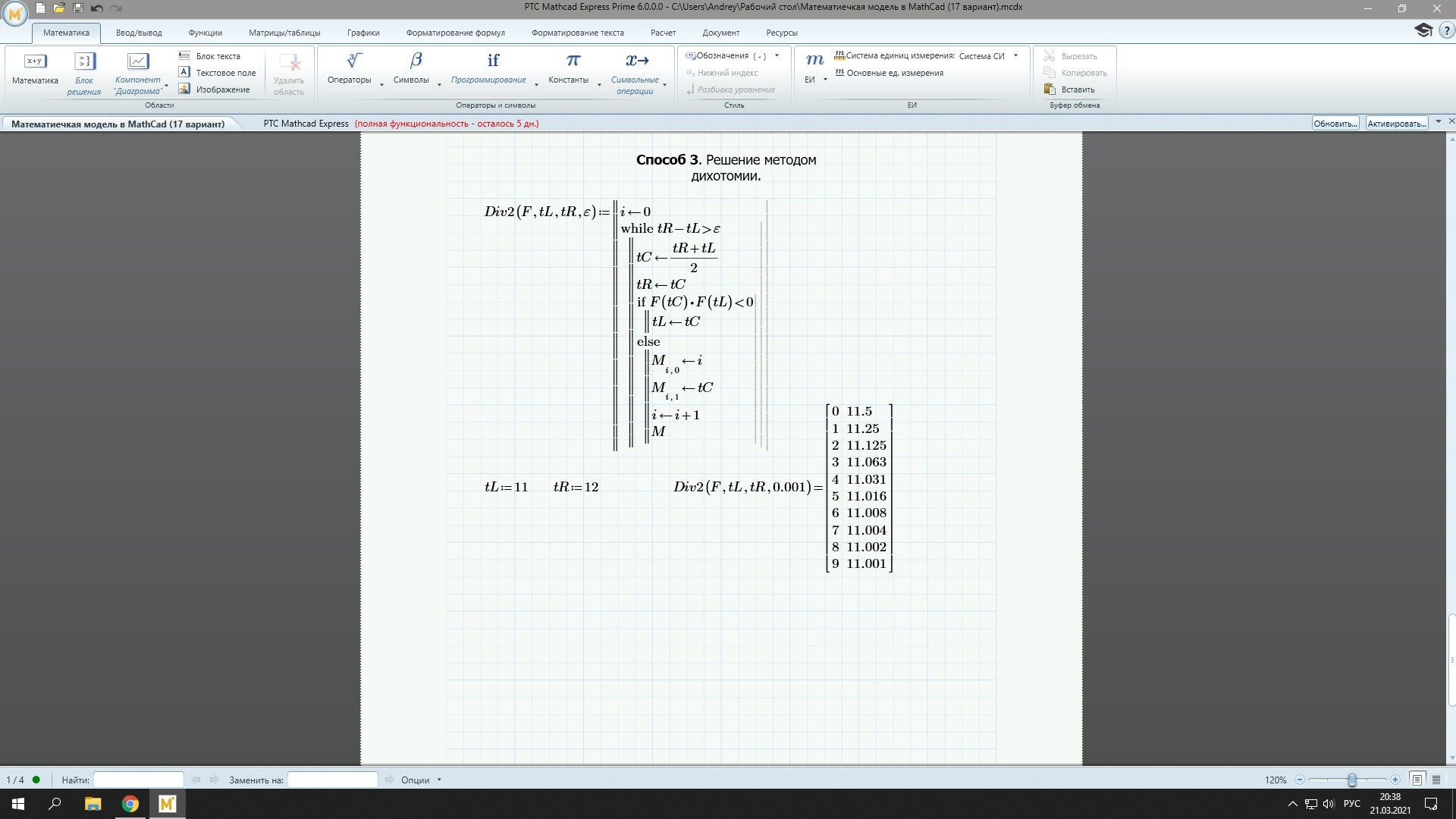
Рис.10. Результаты решения задачи о замене оборудования методом хорд
2 Решение задачи об определении оптимальных сроков замены оборудования в MS Excel 2.1 Графическое решение задачи об определении оптимальных сроков замены оборудования в MS Excel
Для графического решения задачи в MS Excel необходимо подготовить исходные данные и построить графики функций. В столбце А располагаются значения времени t из заданного интервала: от 1,5 до14,8. В столбце В – значения функции доходов 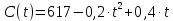 . Функция расходов . Функция расходов 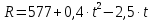 находится в столбце С. Шаг равен 0,7. Меньший шаг даст большую точность, но получится таблица, слишком большая для вставки в документ MS Word. Вид диаграммы точечная (рис.11). находится в столбце С. Шаг равен 0,7. Меньший шаг даст большую точность, но получится таблица, слишком большая для вставки в документ MS Word. Вид диаграммы точечная (рис.11).
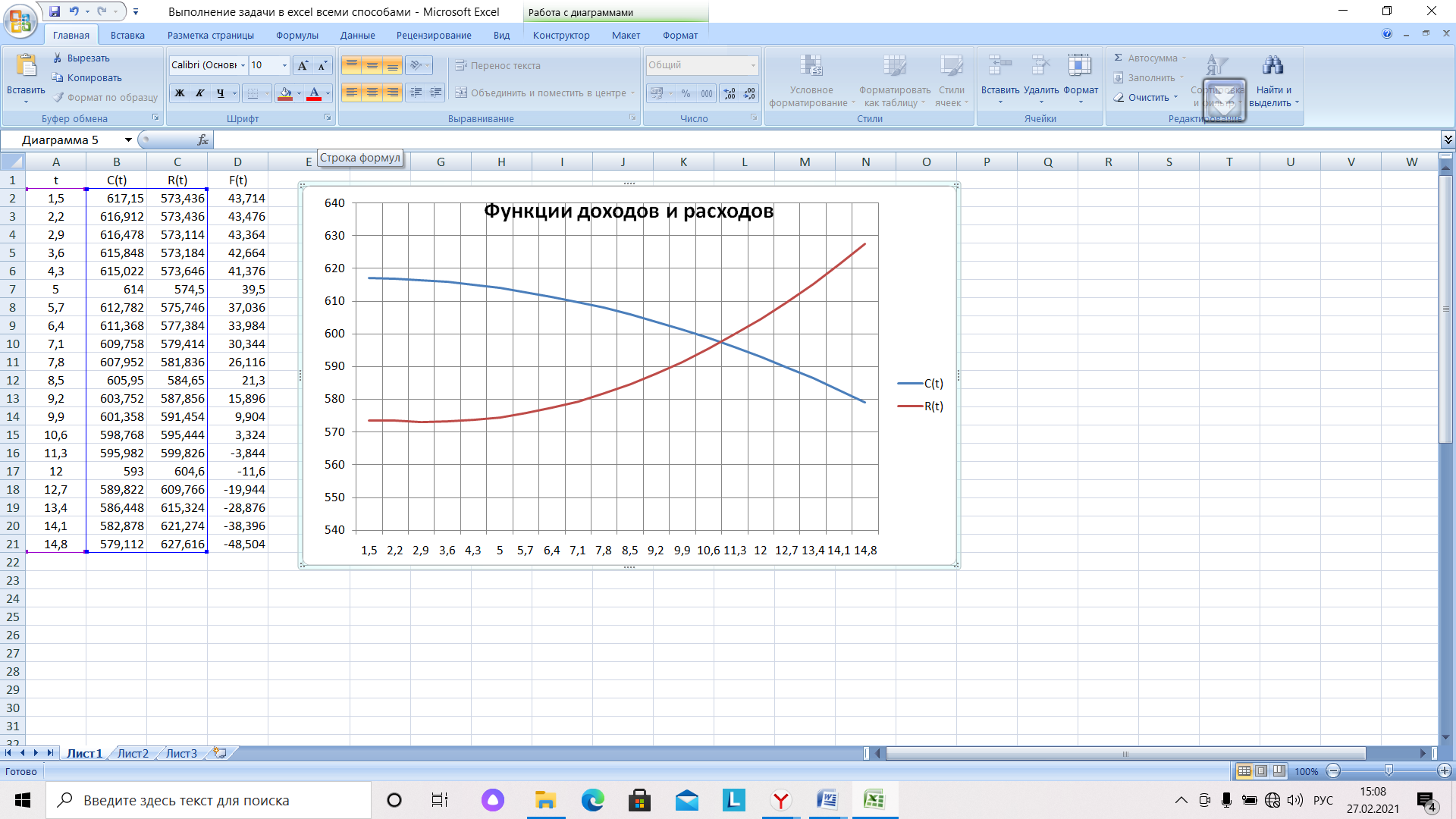
Рис.11. Графики функций доходов и расходов
По диаграмме определяем границы интервала, где находится решение – пересечение графиков функций доходов и расходов. Левое значение равно 9,9, правое – 10,6. Для дальнейших расчетов будем пользоваться одной функцией – функцией прибыли F(t), представляющую собой разность функций доходов и расходов. Искомая точка – пересечение F(t) оси t. Отрицательные значения – когда доходы не превышают расходов, не интересны, поэтому значения F(t) меньше –570, можно игнорировать (рис. 12).
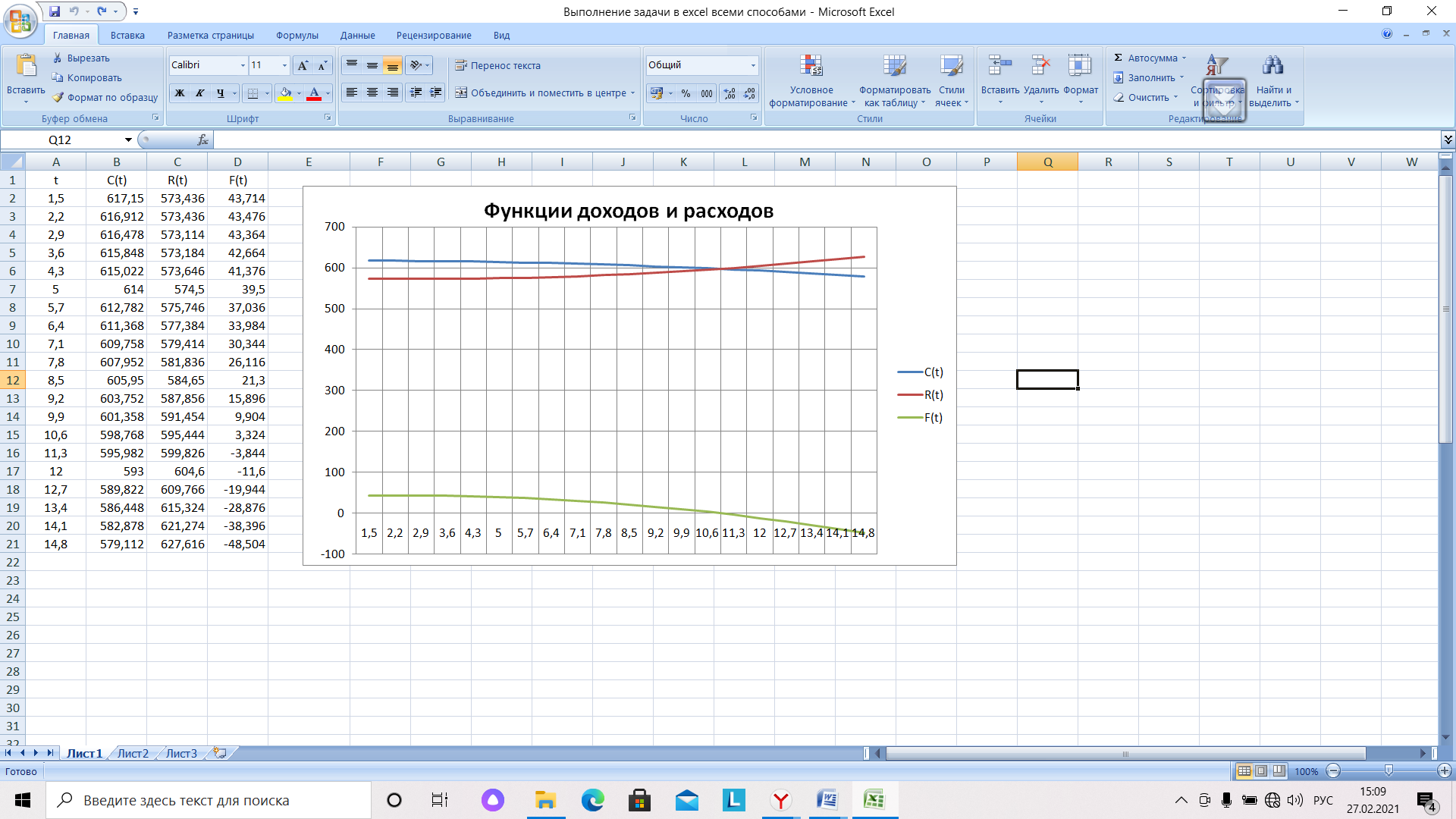
Рис.12. График функции прибыли
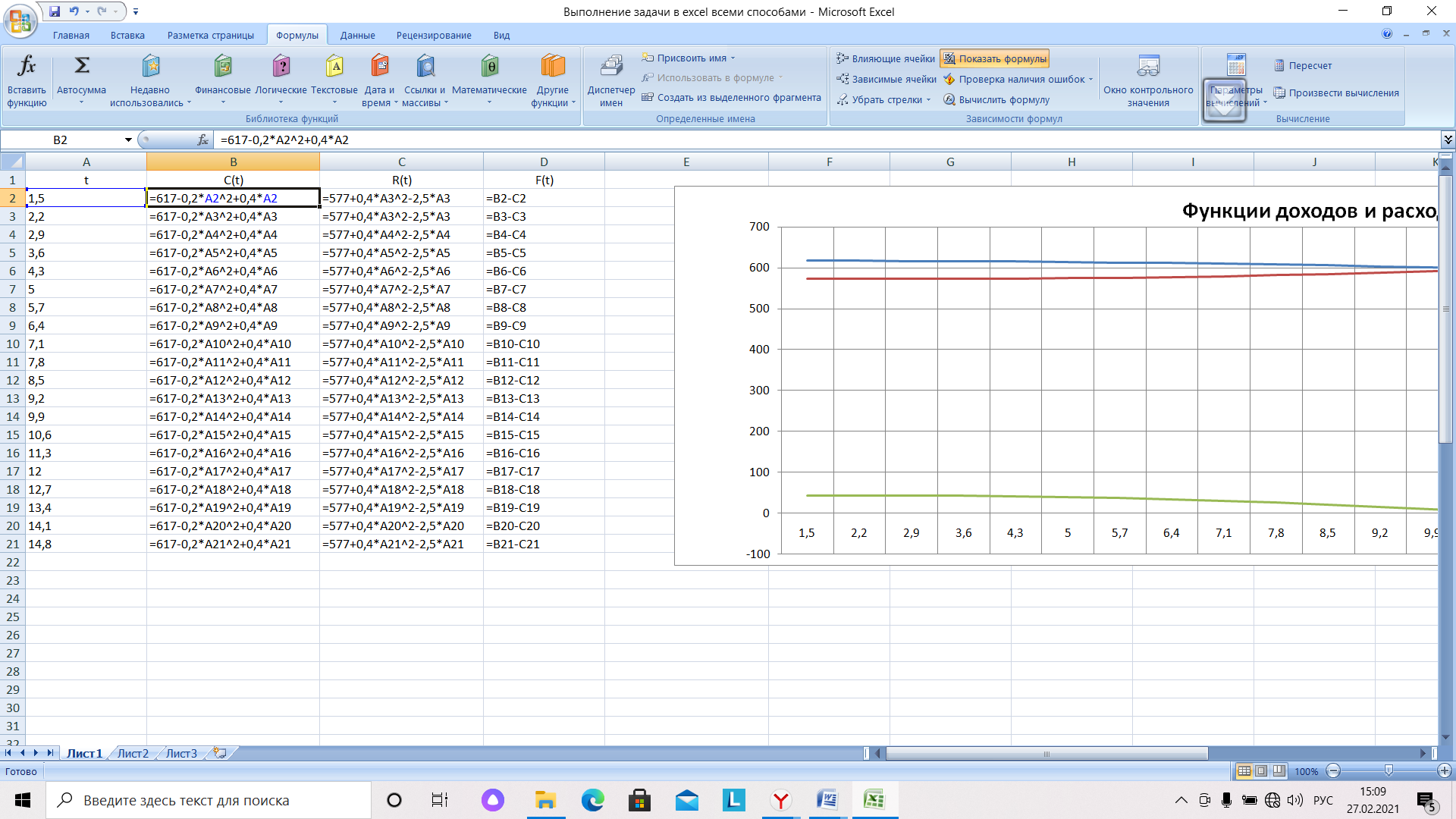
Рис. 13. Фрагмент таблицы с результатами вычислений в режиме отображения формул
Как следует из рисунка 10, решение задачи для функции прибыли F(t), (пересечение оси t) и пересечение функций доходов и расходов совпадают.
2.2 Решение задачи об определении оптимальных сроков замены оборудования в MS Excel методом хорд
В соответствии с методом хорд, разместим в столбце А номер итерации, в столбце В – момент времени, рекомендованный для замены оборудования. В столбец С записывается функция прибыли. В принципе, для достижения цели работы этого достаточно. Но для оценки погрешности потребуется еще производная от функции прибыли, запишем ее в столбец D, и непосредственно, сама погрешность ε в столбце Е. Отдельно записываются границы интервала и значение функции для неподвижного конца b (рис. 14).
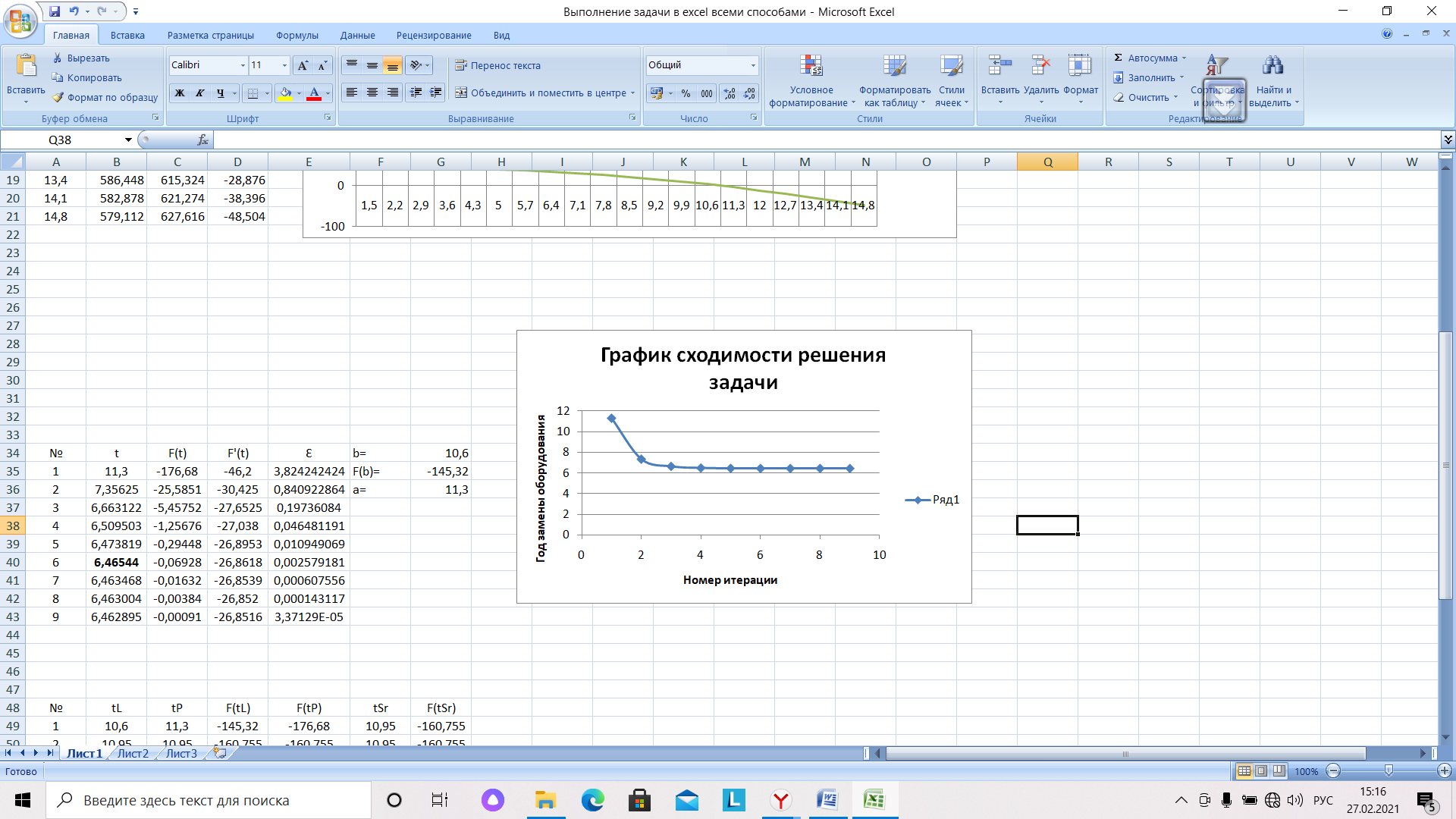
Рис.14. Решение задачи о замене оборудования методом хорд
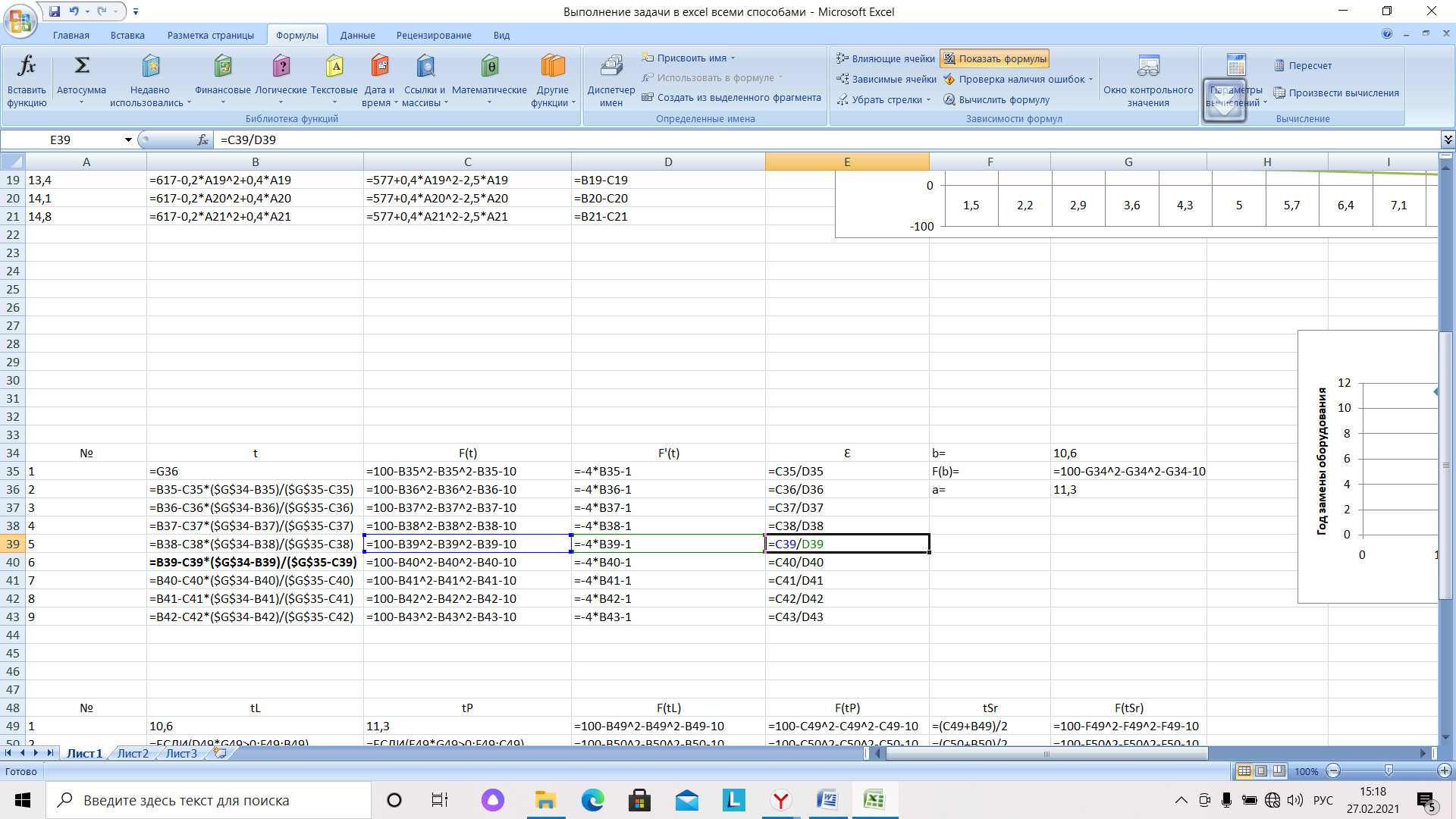
Рис. 15. Фрагмент таблицы с результатами вычислений в режиме отображения формул
2.3 Решение задачи об определении оптимальных сроков замены оборудования в MS Excel методом дихотомии
Графическим способом определен интервал, в котором находится решение задачи. Начальные значения помещены в ячейки В35 и С35. В следующих столбцах будут находиться значения функции прибыли. В соответствии с теоретическими основами метода дихотомии, в следующих двух столбцах будут находиться среднее значение времени t и значение функции прибыли в данной точке. Начальные значения определяют первую строку таблицы (рис. 16).
Основная идея метода дихотомии сосредоточена в столбцах В и С. Проверка, совпадает ли знак функции на краю со знаком функции в середине интервала реализована следующим образом: если знак произведения данных функций больше нуля, то знаки совпадают, если меньше нуля – знаки различаются.
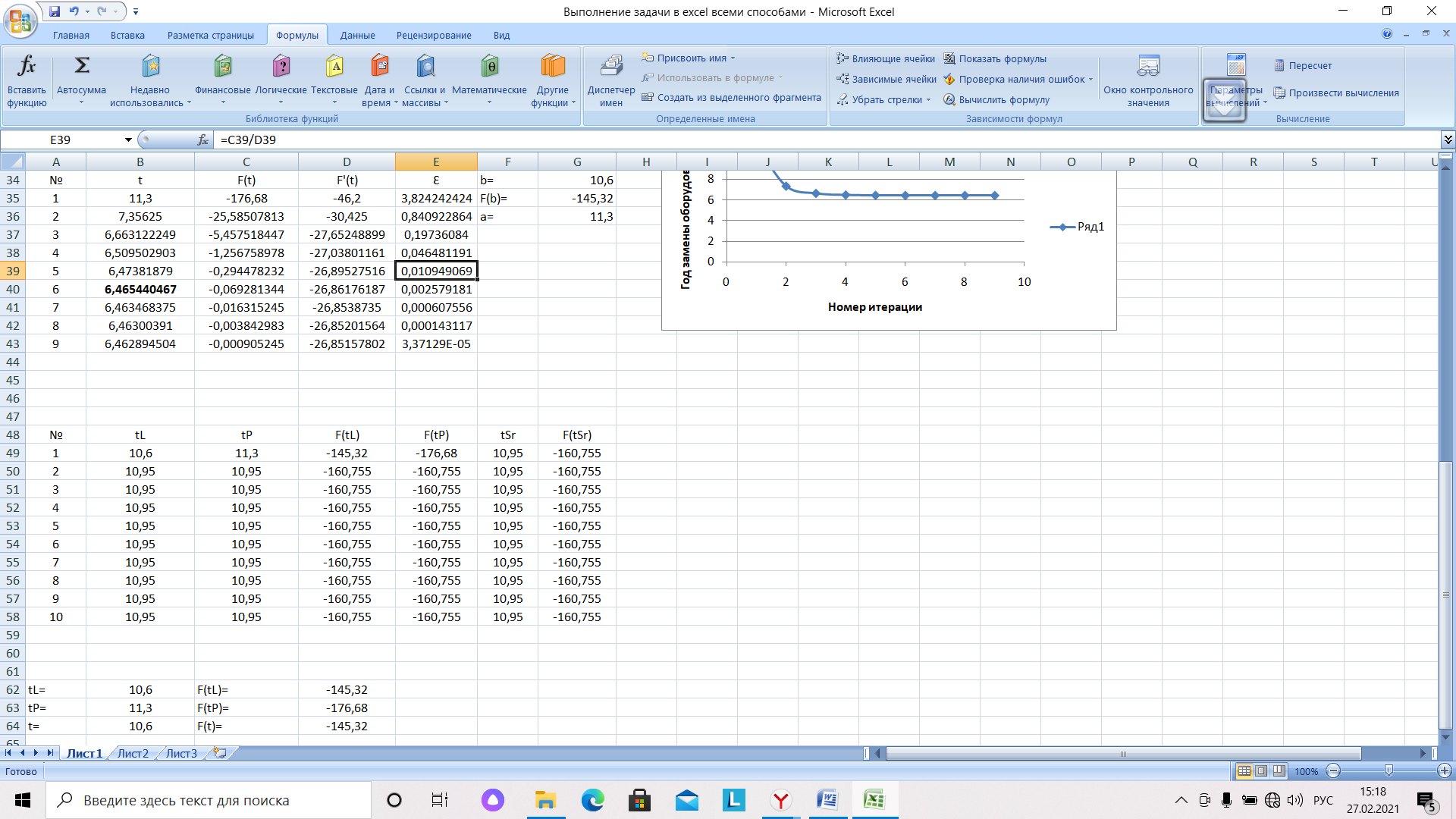
Рис.16. Решение задачи в MS Excel методом дихотомии
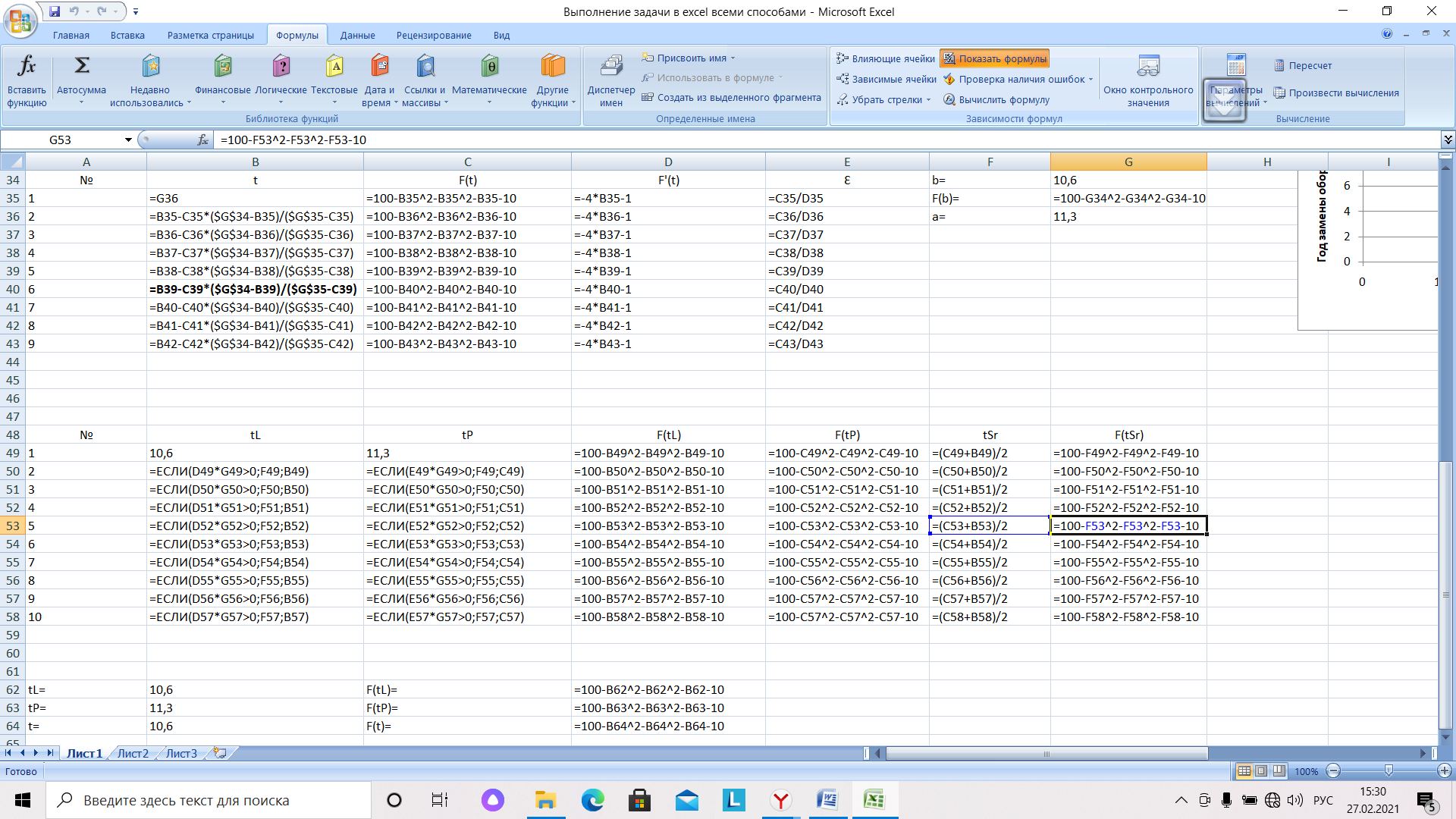
Рис. 17. Фрагмент таблицы с результатами вычислений в режиме отображения формул
Итерационный процесс заканчивается, когда погрешность станет меньше заданной. Представленный на рисунке 18 график сходимости решения показывает, что несмотря на существенные отклонения, решение сходится к значению, совпадающему с решениями другими методами.
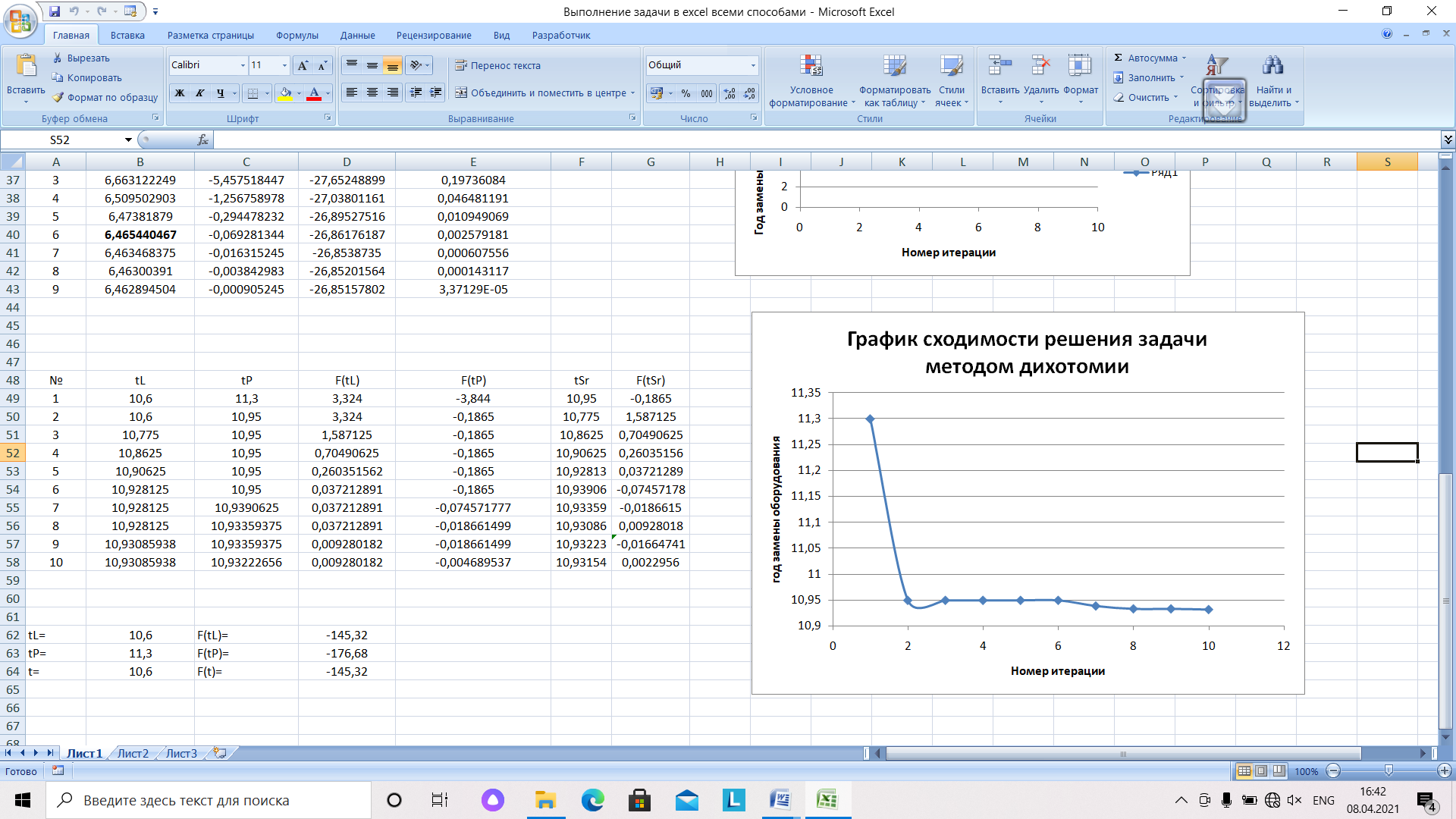
Рис.18. График сходимости решения задачи методом дихотомии
Если сравнивать сходимость методов хорд и дихотомии, то очевидно, что сходимость по методу хорд лучше, так как заданная точность достигается за меньшее число шагов.
2.4 Решение задачи об определении оптимальных сроков замены оборудования с помощью надстройки «Поиск решения»
Для решения задачи с помощью надстройки «Поиск решения», выполним ряд подготовительных действий. Прежде всего предусмотрим ячейку, в которой будет находиться ответ – это В64. Искомое значение должно обеспечить значение целевой функции, близкое к нулю. Запишем ее в ячейку D64 с соответствующей функцией. Оптимальное значение должно находиться в пределах tL – tP, которые были определены графическим методом. Эти числа указываем непосредственно в окне настройки «Поиска решения», но и в ячейки листа MS Excel добавим их, чтобы было нагляднее. Рассчитаем для них значения целевой функции, что является дополнительной защитой от ошибок: у значений должны быть разные знаки.
Целевая ячейка – значение функции в искомой точке. Указываем, что она должна быть равна нулю. Далее вводим адрес ячейки, значение которой подбирается – В64. Кроме естественных ограничений, которые представлены пунктом «Сделать переменные без ограничений неотрицательными», ограничим будущее решение тем интервалом, где по графику находится решение. В данном случае, это более строгое ограничение, чем просто неотрицательные значения. Решение задачи с помощью надстройки «Поиск решения» представлено на рисунке 19:
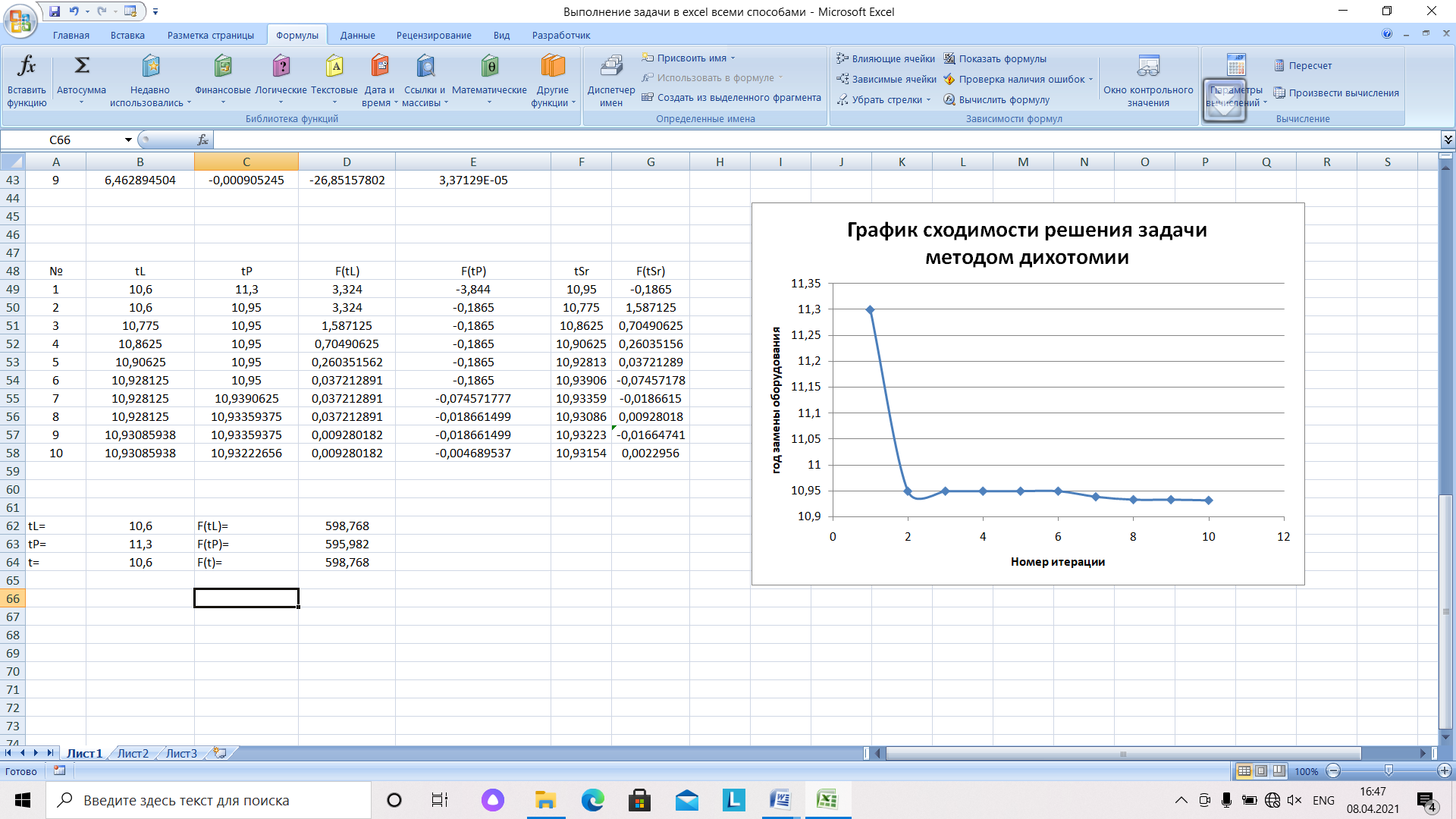
Рис.19. Результаты решения задачи в надстройке «Поиск решения»
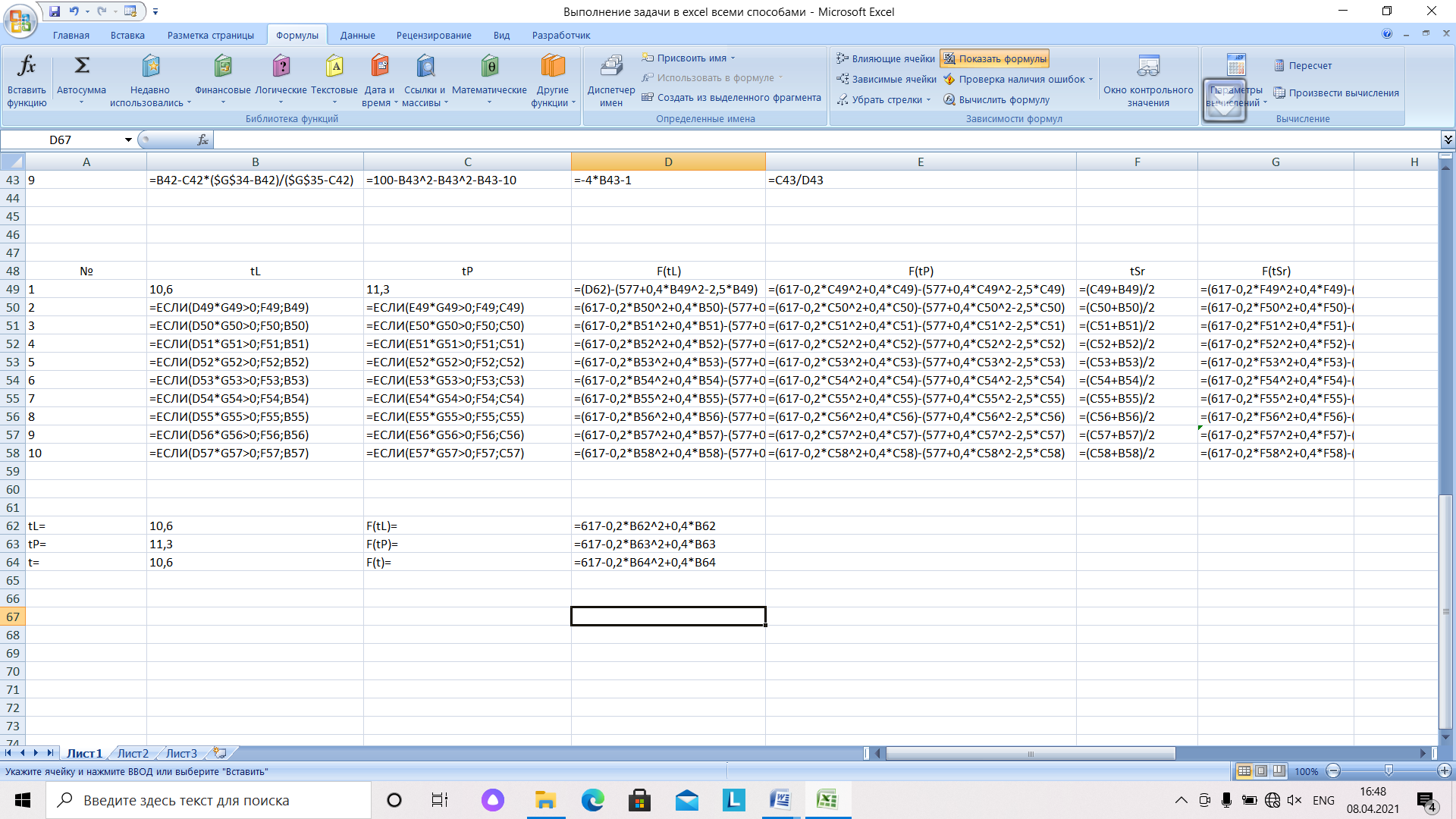
Рис.20. Фрагмент таблицы с результатами вычислений в режиме отображения форму
3 Решение задачи об определении оптимальных сроков замены оборудования средствами Visual Basic For Applications
Для построения графика понадобятся следующий инструменты:
Toolbox
Listbox
Label
Image
Commandbutton
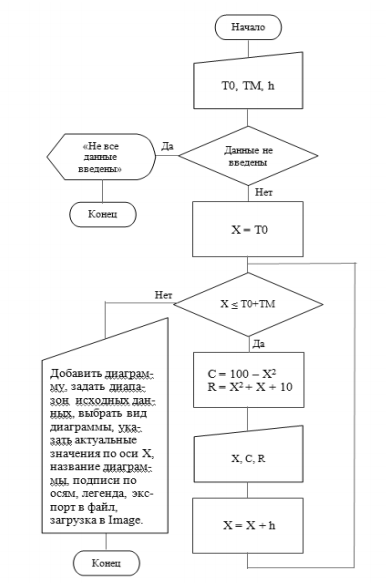
Рис.21. Алгоритм расчета и построения графиков
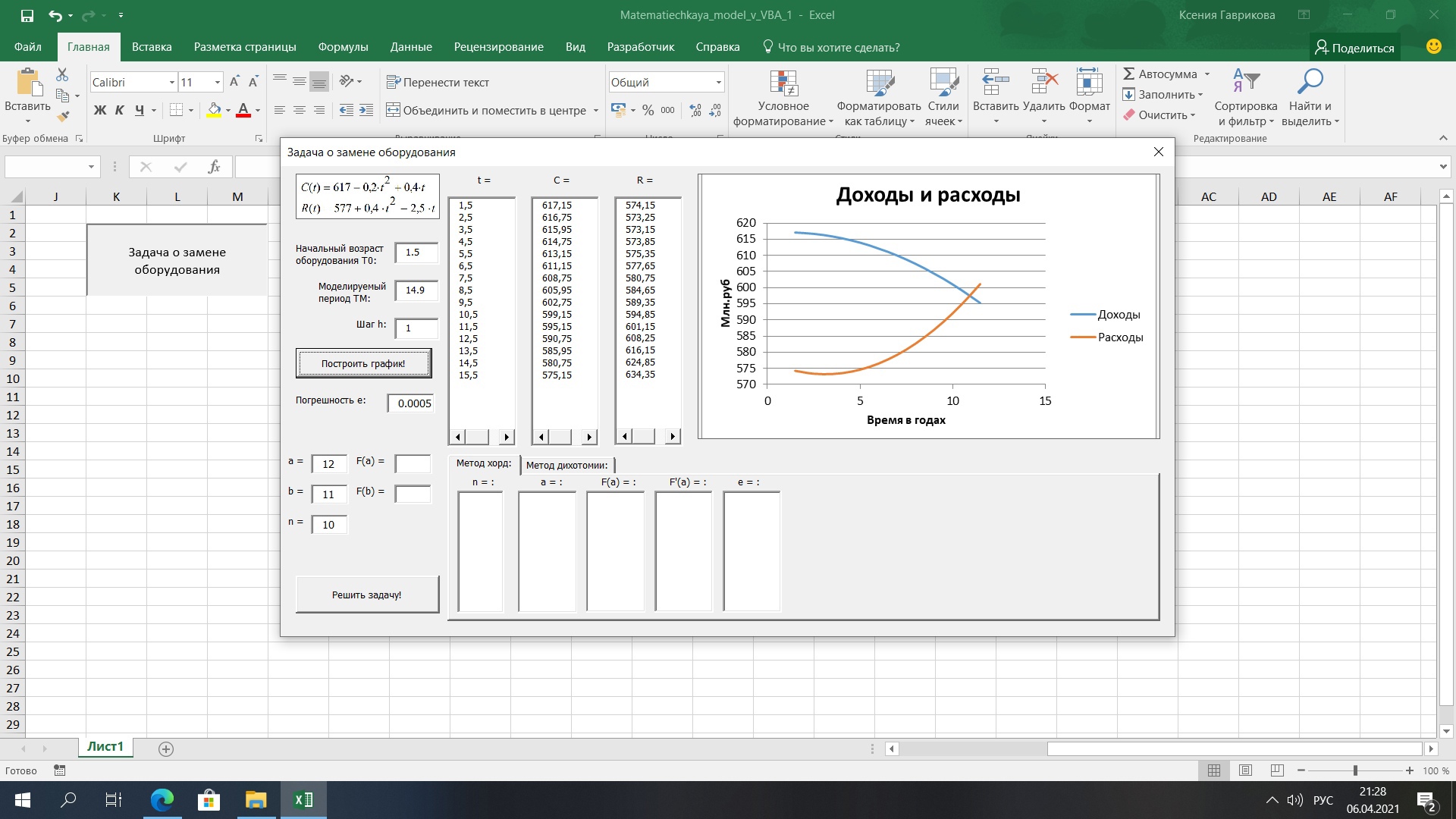
Рис.22. Результаты решения задачи графическим способом
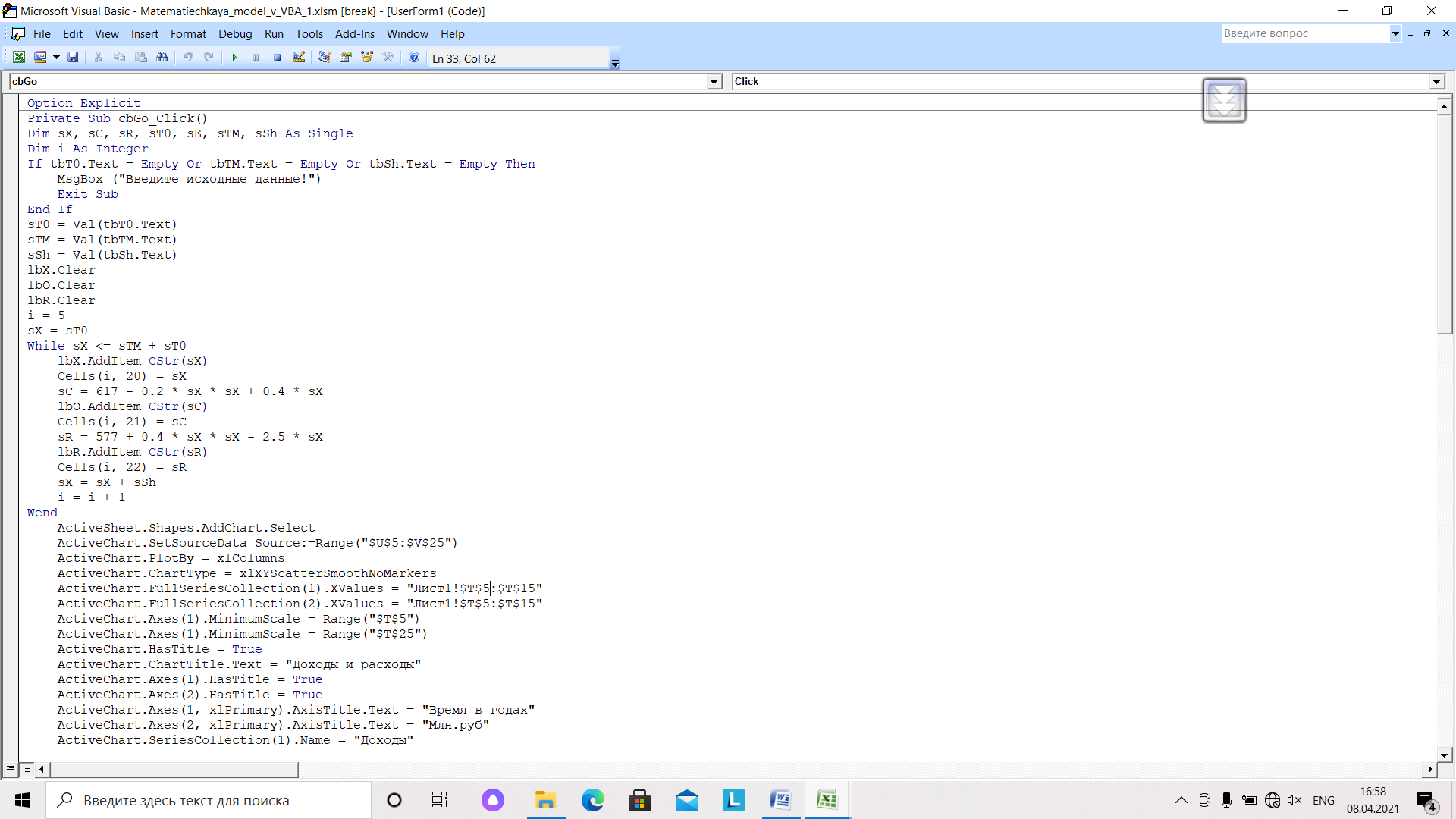
Рис.23. Программа, реализующая ввод исходных данных и проверка их на полноту
Выполнение итераций в цикле. Первая строчка начинает счет с пятой строки.
Далее счет идет до конца периода моделирования. В лист Excel записываются текущие данные и потом они выводятся в UserForm.
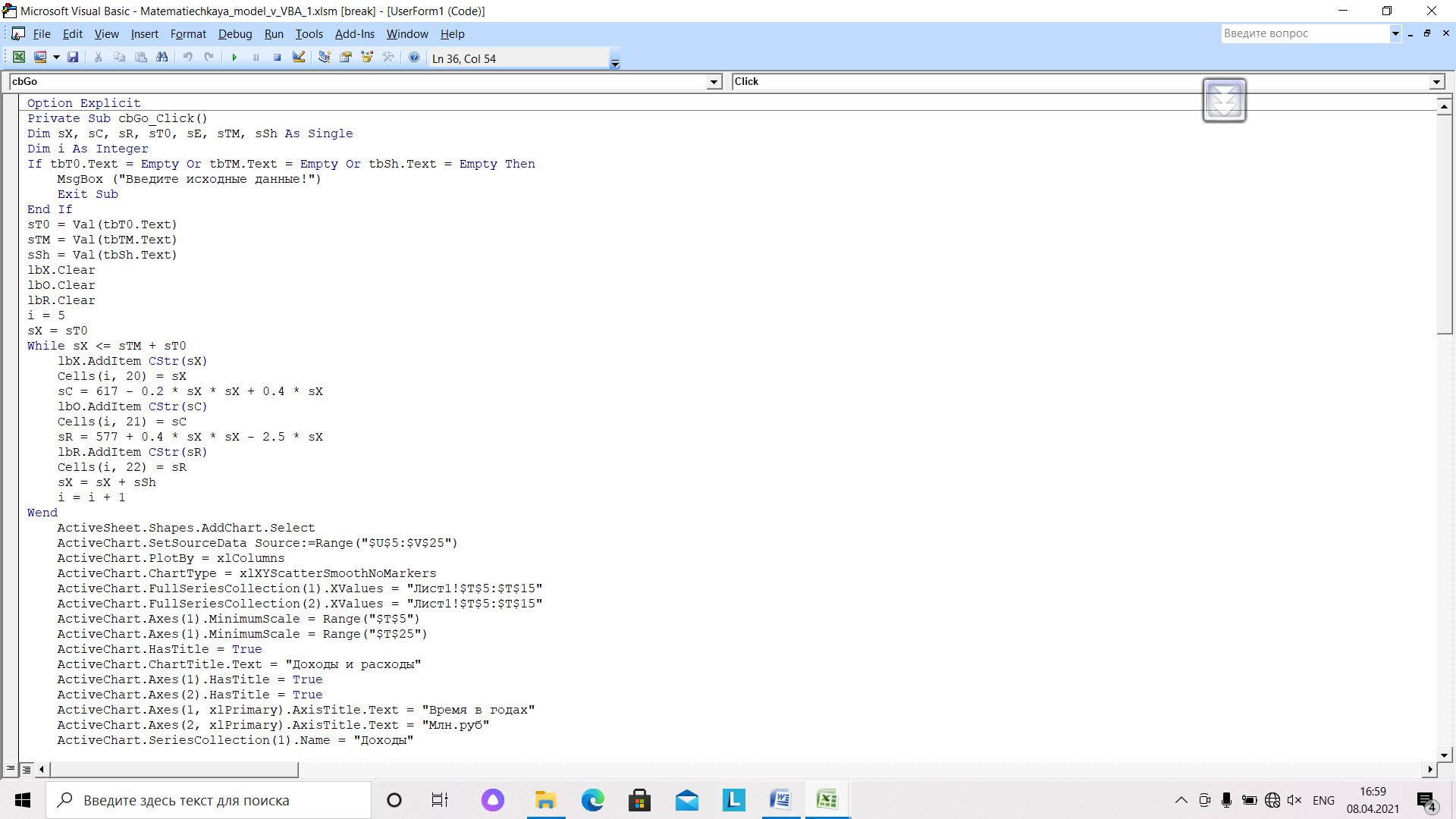
Рис.24. Табулирование аргумента Х и вычисление значений функций C(X) и R(X)
Из рабочего листа в заданном промежутке (строки 5-8) берутся значения функций и переменных. Задаются вид графика, название и наименования осей. Готовый вид графика выводится в Image.
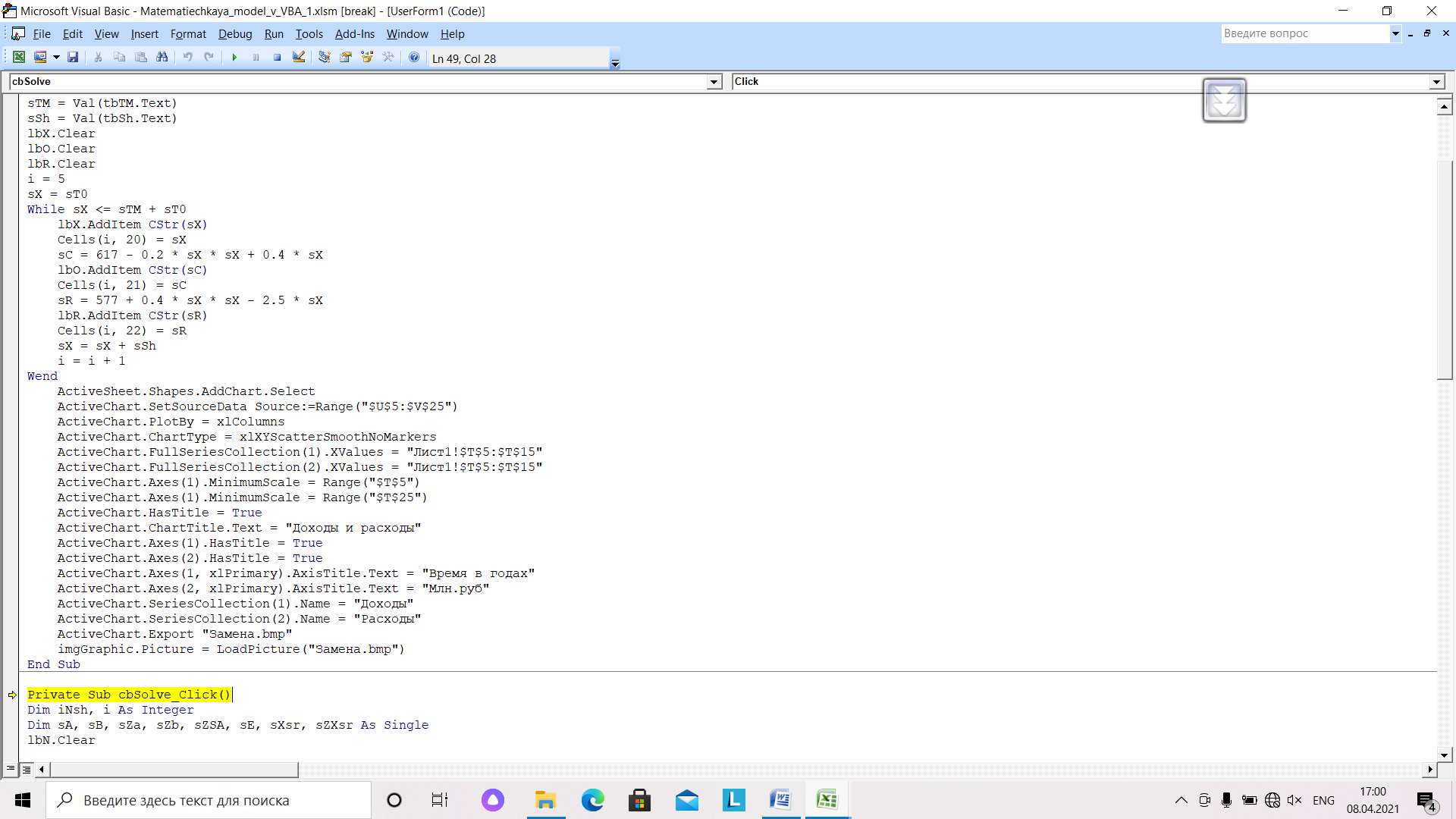
Рис.25. Программный код построения графиком и отображение их на экранной форме
Запуск второй программы осуществляется нажатием кнопки с названием «Решить задачу» и с именем cbSolve. Алгоритм этой части программы выглядит следующим образом (рис. 26).
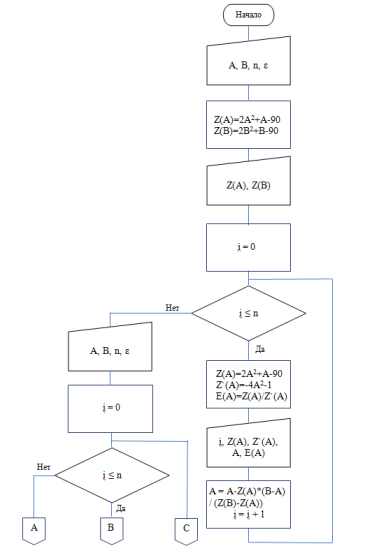
Рис.26. Алгоритм решения задачи методами хорд и дихотомии (начало)
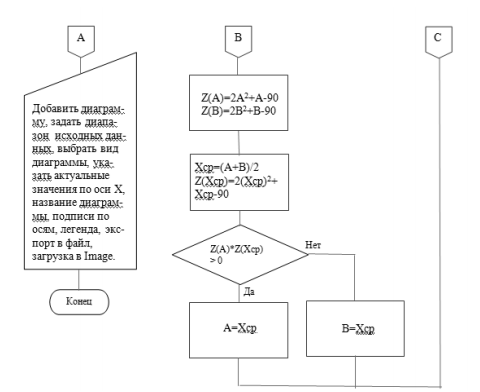
Рис.27. Алгоритм решения задачи методами хорд и дихотомии (окончание)
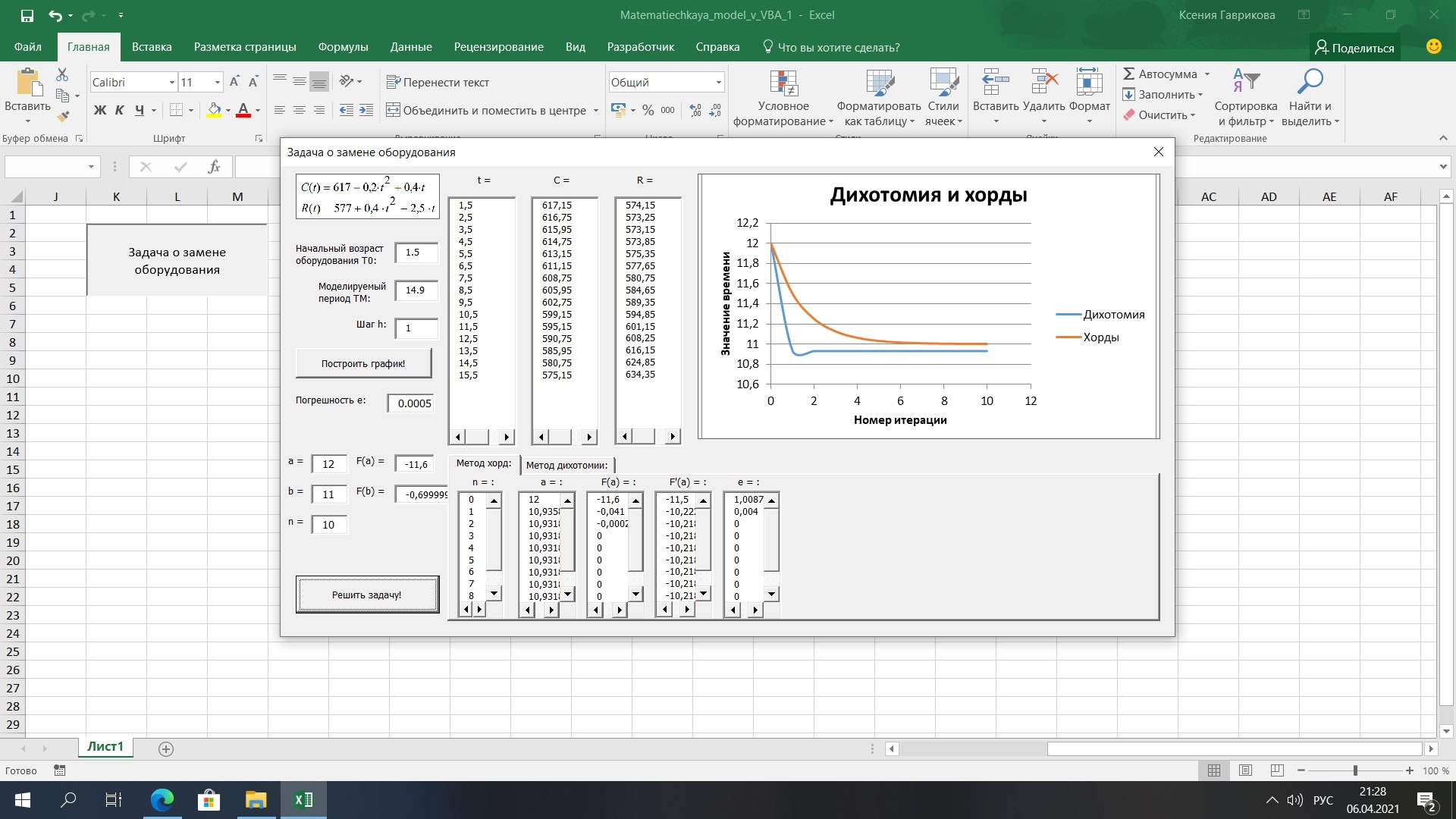
Рис.28. Экранная форма с решением задачи методом хорд
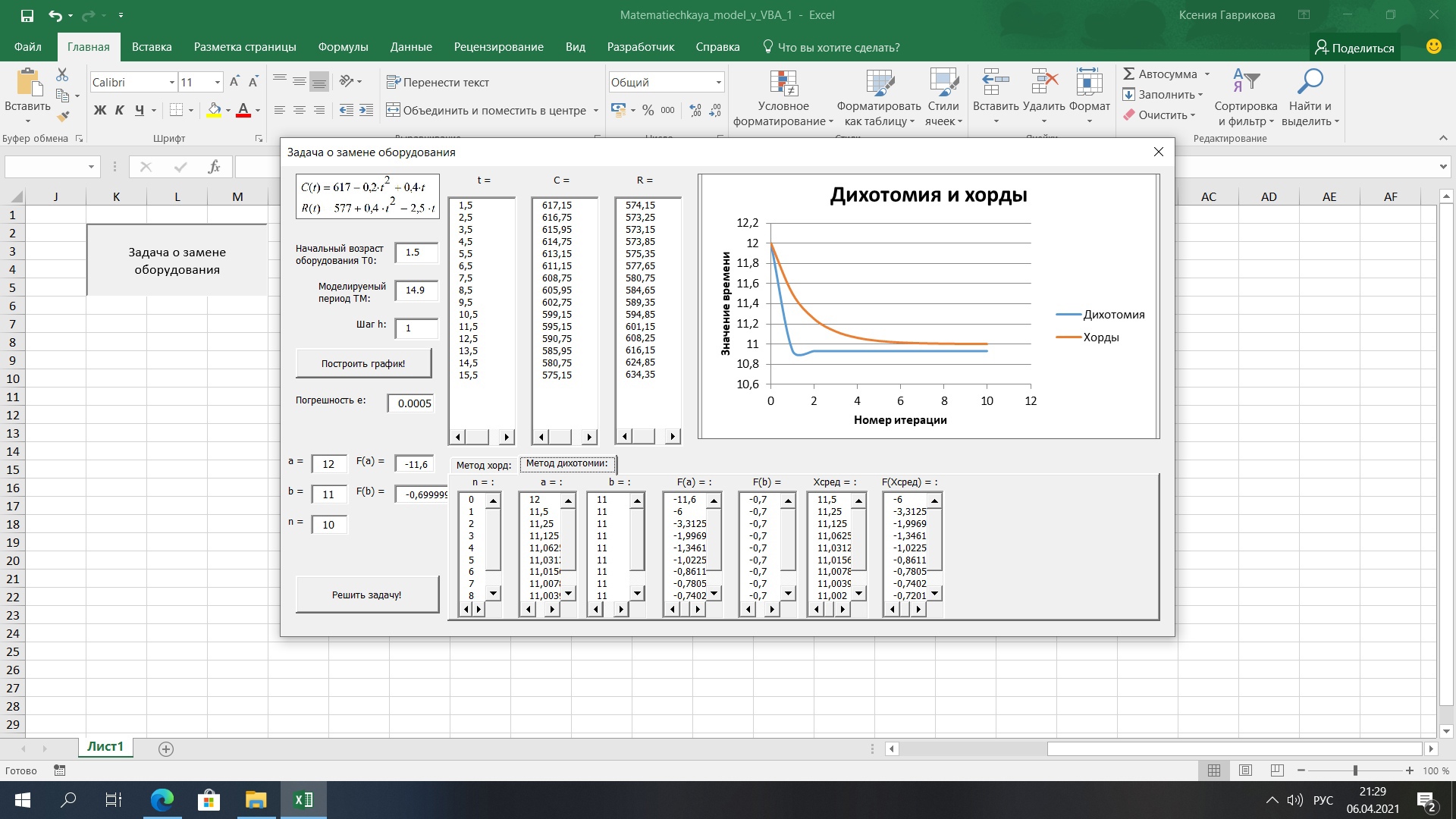
Рис.29. Экранная форма с решением задачи методом дихотомии
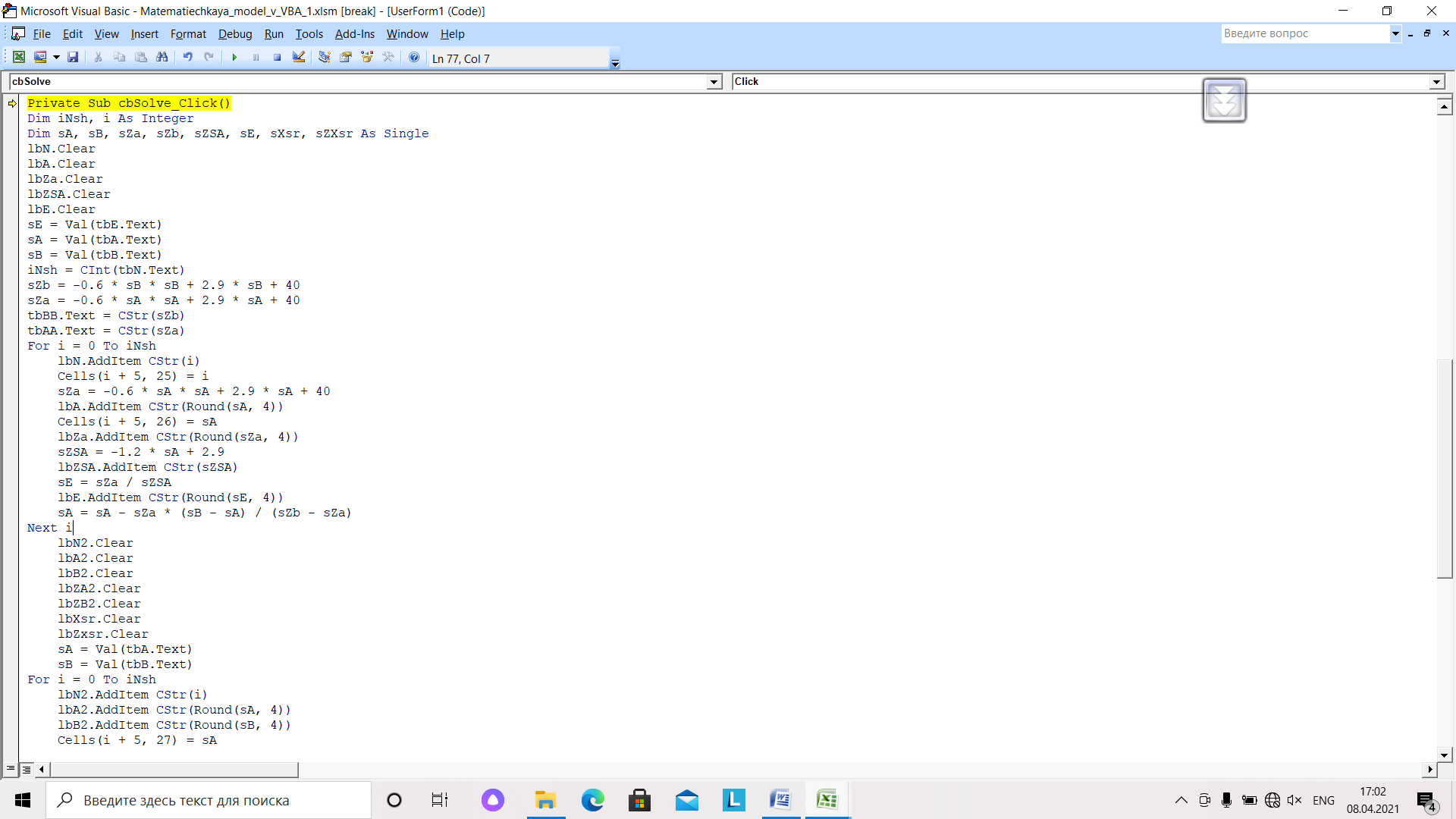
Рис.30. Алгоритм решения задачи методами хорд и дихотомии
Находим решение методом хорд и половинного деления. Все действия выполняются итерацией в цикле.
Шаг записывается в ЛистБокс и на лист. Вычисляем значение функции на конце интервала и округляем его до 4 знаков. Вычисляем значение производной в подвижной точке Х и записываем его в ЛистБокс.
Рассчитываем погрешность и тоже записываем в ЛистБокс.
Находим еще одно значение подвижного конца.

Рис.31. Программа, реализующая метод хорд
Считываем исходные данные с ТекстБоксов. Далее помещаем в Листбоксы значения концов промежутка и номер итерации.
Вычисляем значение функции на обоих концах промежутка и в середине интервала, затем записываем в ЛистБокс.
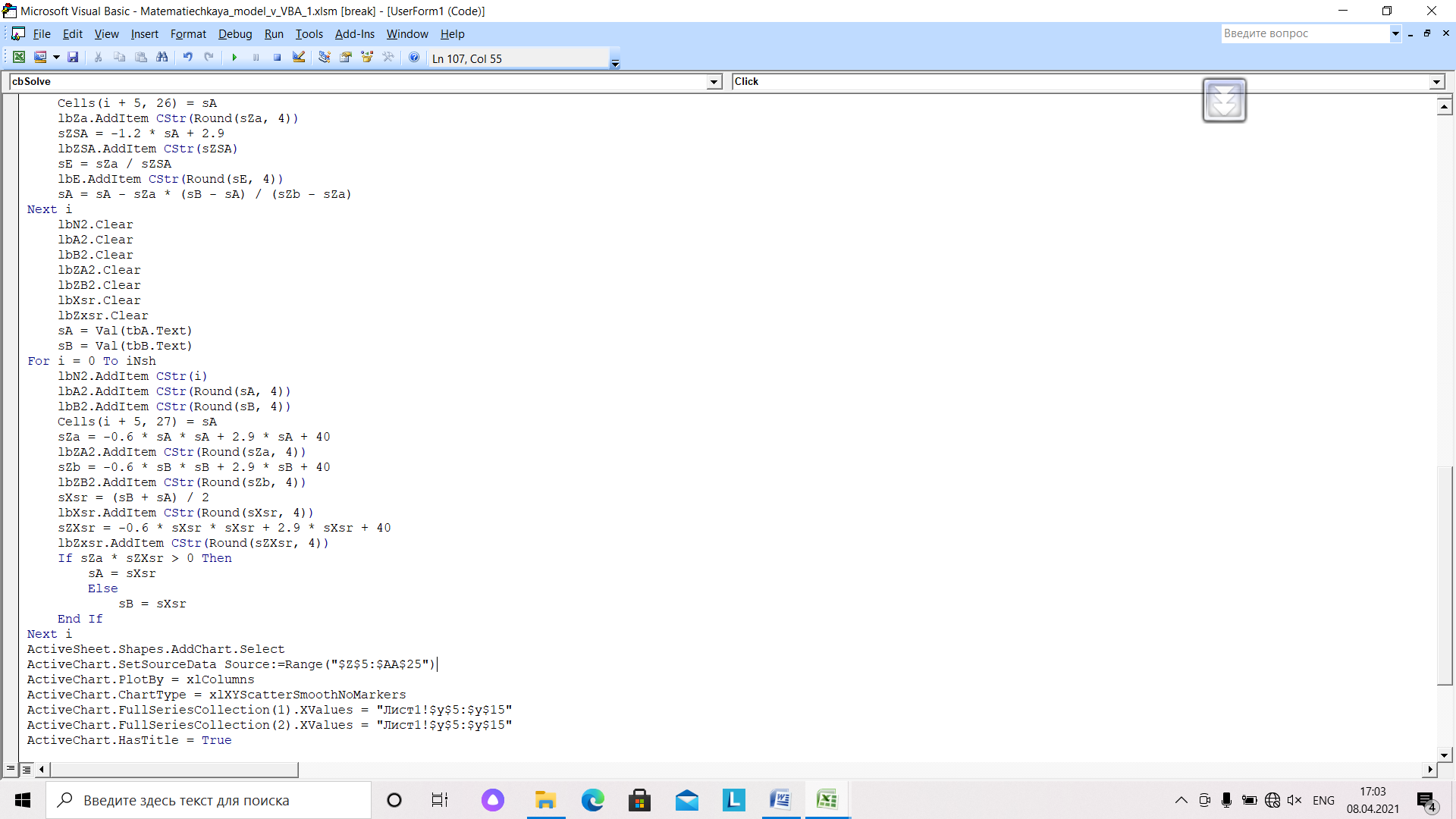
Рис.32. Программа, реализующая метод дихотомии
После выполнения всех расчетов строим график сравнения сходимости решения по методу хорд и дихотомии.
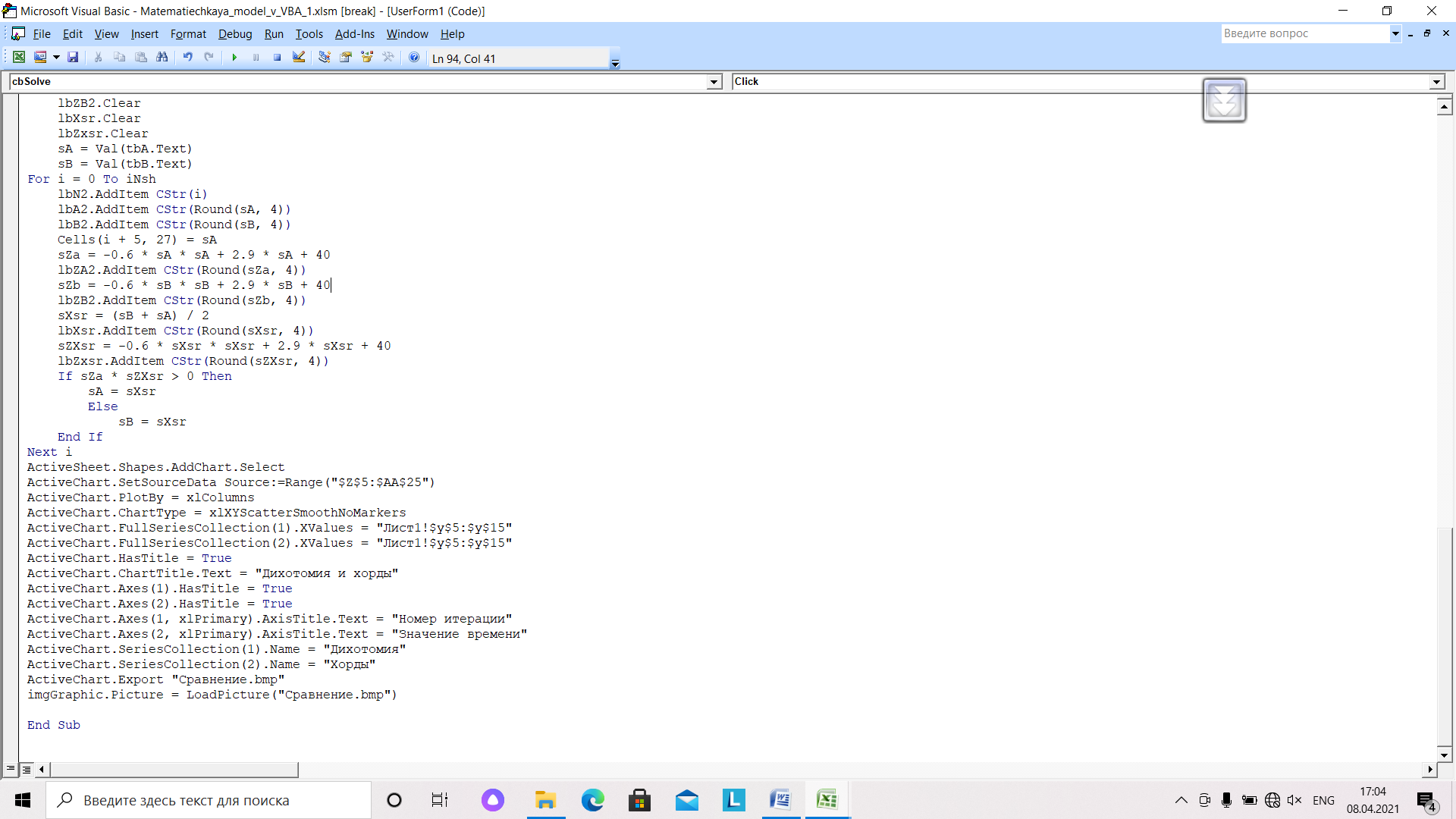
Рис.33. Программа построения графиков, сравнения сходимости методов хорд и дихотомии
Заключение
В данной курсовой работе был проведён расчёт оптимальных сроков замены оборудования посредством нескольких компьютерных программ: табличного процессора Microsoft Excel, математического пакета MathCAD, а также в среде программирования Visual Basic for Applications. Выполнение всех действий в программных пакетах полностью подготовлено содержанием курса «Информатика», освоенного в Горном университете.
Использованием компьютера в вычислительной части однозначно облегчает расчёт оптимальных сроков замены оборудования. При работе в табличном процессоре MS Excel, благодаря большому количеству встроенных функций, существенно уменьшается время, затрачиваемое на вычисления, и появляется возможность построения графического варианта эпюр.
Решение средствами пакета MathCAD является самым наглядным решением из всех решений с использованием компьютера. Все формулы сохраняют свой вид или изменяются незначительно. При этом порядок действий для решения конкретной задачи легко прослеживается из-за особенностей пакета MathCAD.
В результате работы в среде программирования VBA программа достаточно проста для использования и способна рассчитывать оптимальные сроки замены оборудования с помощью графического метода, а также метода хорд и дихотомии.
По завершению курсовой работы и проверки данных выявлено, что все значения в различных компьютерных программах, а также графики совпадают.
Список использованной литературы
1. Воробьева Ф.И. Информатика. MS Excel 2010: учебное пособие / Ф.И. Воробьева, Е.С. Воробьев. Казань. КНИТУ. 2014. 100 с. http://biblioclub.ru/index.php?page=book&id=428798 (Дата обращения 07.04.2021).
2. Грошев А.С. Информатика: учебник для вузов / А.С. Грошев. - Москва; Берлин: Директ-Медиа. 2015. 484 с. http://biblioclub.ru/index.php?page=book&id=428591 (Дата обращения 07.04.2021).
3. Грошев А.С. Информационные технологии: лабораторный практикум / А.С. Грошев. - 2-е изд. - Москва; Берлин: Директ-Медиа. 2015. 285 с. http://biblioclub.ru/index.php?page=book&id=434666 (Дата обращения 07.04.2021).
4. Агафонов Е.Д. Прикладное программирование: учебное пособие / Е.Д. Агафонов, Г.В. Ващенко. Красноярск: Сибирский федеральный университет. 2015. 112 с. http://biblioclub.ru/index.php?page=book&id=43564 (Дата обращения 07.04.2021).
5. Половко А. М. Mathcad для студента / А. М. Половко, И. В. Ганичев.- СПб: БХВ-Петербург, 2006, 336с (Дата обращения 07.04.2021).
Приложение 1. Листинг кода
Часть кода 1
Option Explicit
Private Sub cbGo_Click()
Dim sX, sC, sR, sT0, sE, sTM, sSh As Single
Dim i As Integer
If tbT0.Text = Empty Or tbTM.Text = Empty Or tbSh.Text = Empty Then
MsgBox ("Ââåäèòå èñõîäíûå äàííûå!")
Exit Sub
End If
sT0 = Val(tbT0.Text)
sTM = Val(tbTM.Text)
sSh = Val(tbSh.Text)
lbX.Clear
lbO.Clear
lbR.Clear
i = 5
sX = sT0
While sX <= sTM + sT0
lbX.AddItem CStr(sX)
Cells(i, 20) = sX
sC = 617 - 0.2 * sX * sX + 0.4 * sX
lbO.AddItem CStr(sC)
Cells(i, 21) = sC
sR = 577 + 0.4 * sX * sX - 2.5 * sX
lbR.AddItem CStr(sR)
Cells(i, 22) = sR
sX = sX + sSh
i = i + 1
Wend
ActiveSheet.Shapes.AddChart.Select
ActiveChart.SetSourceData Source:=Range("$U$5:$V$25")
ActiveChart.PlotBy = xlColumns
ActiveChart.ChartType = xlXYScatterSmoothNoMarkers
ActiveChart.FullSeriesCollection(1).XValues = "Ëèñò1!$T$5:$T$15"
ActiveChart.FullSeriesCollection(2).XValues = "Ëèñò1!$T$5:$T$15"
ActiveChart.Axes(1).MinimumScale = Range("$T$5")
ActiveChart.Axes(1).MinimumScale = Range("$T$25")
ActiveChart.HasTitle = True
ActiveChart.ChartTitle.Text = "Äîõîäû è ðàñõîäû"
ActiveChart.Axes(1).HasTitle = True
ActiveChart.Axes(2).HasTitle = True
ActiveChart.Axes(1, xlPrimary).AxisTitle.Text = "Âðåìÿ â ãîäàõ"
ActiveChart.Axes(2, xlPrimary).AxisTitle.Text = "Ìëí.ðóá"
ActiveChart.SeriesCollection(1).Name = "Äîõîäû"
ActiveChart.SeriesCollection(2).Name = "Ðàñõîäû"
ActiveChart.Export "Çàìåíà.bmp"
imgGraphic.Picture = LoadPicture("Çàìåíà.bmp")
End Sub
Часть кода 2
Private Sub cbSolve_Click()
Dim iNsh, i As Integer
Dim sA, sB, sZa, sZb, sZSA, sE, sXsr, sZXsr As Single
lbN.Clear
lbA.Clear
lbZa.Clear
lbZSA.Clear
lbE.Clear
sE = Val(tbE.Text)
sA = Val(tbA.Text)
sB = Val(tbB.Text)
iNsh = CInt(tbN.Text)
sZb = -0.6 * sB * sB + 2.9 * sB + 40
sZa = -0.6 * sA * sA + 2.9 * sA + 40
tbBB.Text = CStr(sZb)
tbAA.Text = CStr(sZa)
For i = 0 To iNsh
lbN.AddItem CStr(i)
Cells(i + 5, 25) = i
sZa = -0.6 * sA * sA + 2.9 * sA + 40
lbA.AddItem CStr(Round(sA, 4))
Cells(i + 5, 26) = sA
lbZa.AddItem CStr(Round(sZa, 4))
sZSA = -1.2 * sA + 2.9
lbZSA.AddItem CStr(sZSA)
sE = sZa / sZSA
lbE.AddItem CStr(Round(sE, 4))
sA = sA - sZa * (sB - sA) / (sZb - sZa)
Next i
lbN2.Clear
lbA2.Clear
lbB2.Clear
lbZA2.Clear
lbZB2.Clear
lbXsr.Clear
lbZxsr.Clear
sA = Val(tbA.Text)
sB = Val(tbB.Text)
For i = 0 To iNsh
lbN2.AddItem CStr(i)
lbA2.AddItem CStr(Round(sA, 4))
lbB2.AddItem CStr(Round(sB, 4))
Cells(i + 5, 27) = sA
sZa = -0.6 * sA * sA + 2.9 * sA + 40
lbZA2.AddItem CStr(Round(sZa, 4))
sZb = -0.6 * sB * sB + 2.9 * sB + 40
lbZB2.AddItem CStr(Round(sZb, 4))
sXsr = (sB + sA) / 2
lbXsr.AddItem CStr(Round(sXsr, 4))
sZXsr = -0.6 * sXsr * sXsr + 2.9 * sXsr + 40
lbZxsr.AddItem CStr(Round(sZXsr, 4))
If sZa * sZXsr > 0 Then
sA = sXsr
Else
sB = sXsr
End If
Next i
ActiveSheet.Shapes.AddChart.Select
ActiveChart.SetSourceData Source:=Range("$Z$5:$AA$25")
ActiveChart.PlotBy = xlColumns
ActiveChart.ChartType = xlXYScatterSmoothNoMarkers
ActiveChart.FullSeriesCollection(1).XValues = "Ëèñò1!$y$5:$y$15"
ActiveChart.FullSeriesCollection(2).XValues = "Ëèñò1!$y$5:$y$15"
ActiveChart.HasTitle = True
ActiveChart.ChartTitle.Text = "Äèõîòîìèÿ è õîðäû"
ActiveChart.Axes(1).HasTitle = True
ActiveChart.Axes(2).HasTitle = True
ActiveChart.Axes(1, xlPrimary).AxisTitle.Text = "Íîìåð èòåðàöèè"
ActiveChart.Axes(2, xlPrimary).AxisTitle.Text = "Çíà÷åíèå âðåìåíè"
ActiveChart.SeriesCollection(1).Name = "Äèõîòîìèÿ"
ActiveChart.SeriesCollection(2).Name = "Õîðäû"
ActiveChart.Export "Ñðàâíåíèå.bmp"
imgGraphic.Picture = LoadPicture("Ñðàâíåíèå.bmp")
End Sub
|
|
|
 Скачать 7.16 Mb.
Скачать 7.16 Mb.