Курсовая ОИИ. Курсовая работа по дисциплине Основы искусственного интеллекта
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
1.2 Структура экспертной системыСтруктура экспертной системы представлена следующими структурными элементами: База знаний – механизм представления знаний в конкретной предметной области и управления ими; Подсистема логического вывода – делает логические выводы на основании знаний, имеющихся в базе знаний; Пользовательский интерфейс – используется для правильной передачи ответов пользователю; Интерфейс для работы с базой знаний– служит для получения знаний от эксперта и дополнения ее при необходимости; Подсистема объяснения – механизм, способный представлять различные комментарии, прилагаемые к заключению. В противном случае пользователю будет трудно понять заключение. Кроме того, с его помощью эксперт определяет, как работает система, и позволяет точно выяснить, как используются знания, предоставленные им. Ниже представлена структура экспертной системы (рисунок 1). 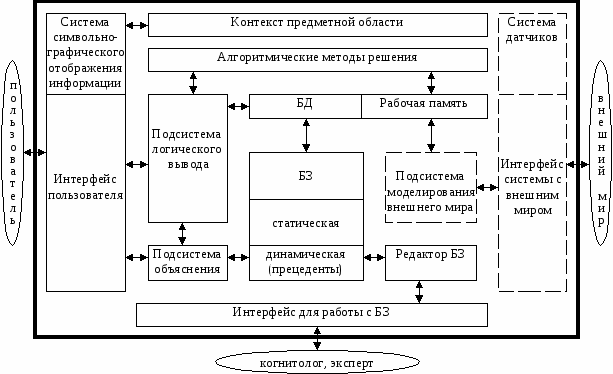 Рисунок - 1 Структура экспертной системы     
1.3 Модели представления знанийОдной из наиболее важных проблем, характерных для систем, основанных на знаниях, является проблема представления знаний. Это объясняется тем, что форма представления знаний оказывает существенное влияние на характеристики и свойства системы. Для того чтобы манипулировать всевозможными знаниями из реального мира с помощью компьютера, необходимо осуществлять их моделирование. В таких случаях необходимо отличать знания, предназначенные для обработки компьютером, от знаний, используемых человеком. П 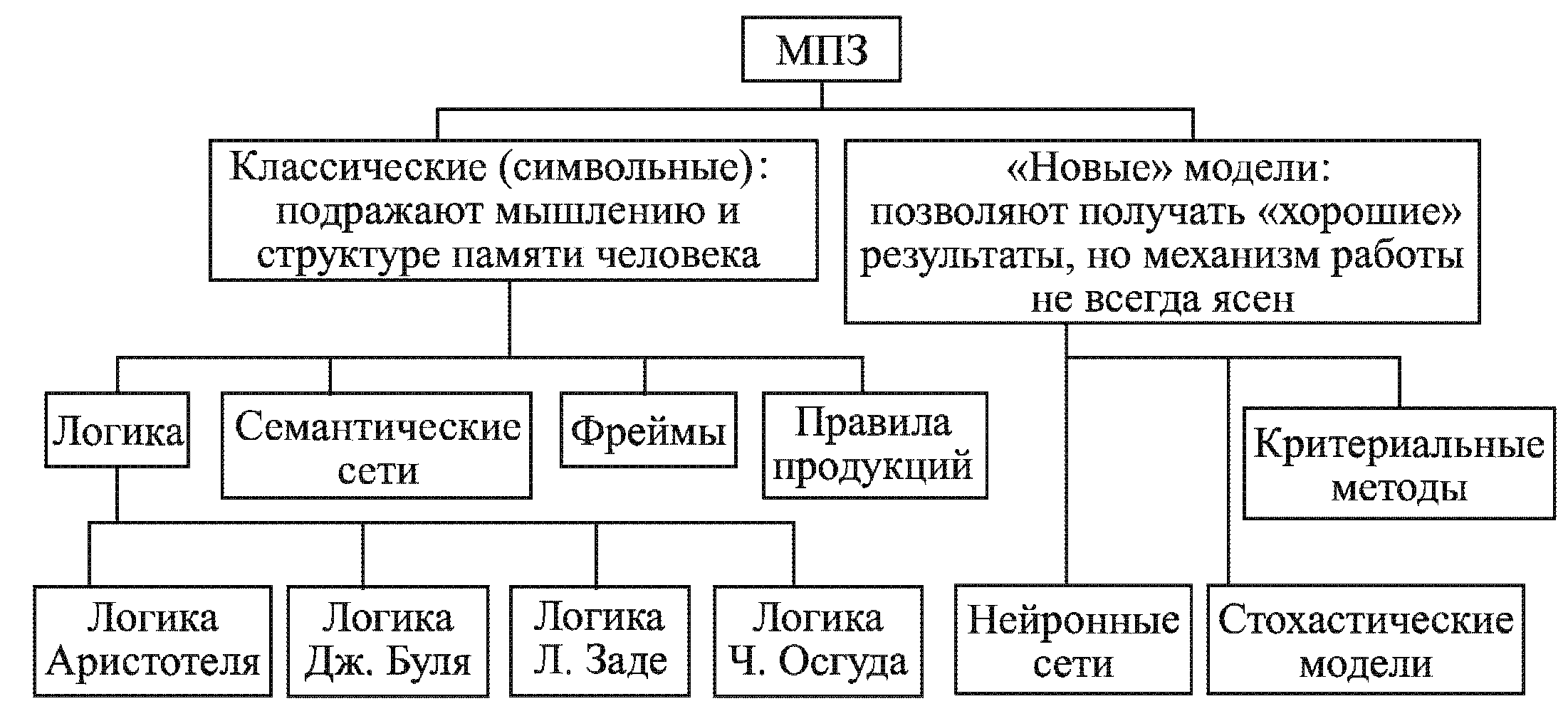 ри проектировании модели представления знаний следует учитывать такие факторы, как однородность представления и простота понимания. Однородное представление приводит к упрощению механизма управления логическим выводом и упрощению управления знаниями. Представление знаний должно быть понятным экспертам и пользователям системы. В противном случае затрудняются приобретение знаний и их оценка. Однако выполнить это требование в равной степени, как для простых, так и для сложных задач довольно трудно. Обычно для несложных задач останавливаются на некотором среднем (компромиссном) представлении, но для решения сложных и больших задач необходимы структурирование и модульное представление. Ниже представлена классификация моделей представления знаний (рисунок 2). ри проектировании модели представления знаний следует учитывать такие факторы, как однородность представления и простота понимания. Однородное представление приводит к упрощению механизма управления логическим выводом и упрощению управления знаниями. Представление знаний должно быть понятным экспертам и пользователям системы. В противном случае затрудняются приобретение знаний и их оценка. Однако выполнить это требование в равной степени, как для простых, так и для сложных задач довольно трудно. Обычно для несложных задач останавливаются на некотором среднем (компромиссном) представлении, но для решения сложных и больших задач необходимы структурирование и модульное представление. Ниже представлена классификация моделей представления знаний (рисунок 2).Рисунок - 2 Классификация моделей представления знаний     
1.3.1 Логическая модель представления знаний Логическая модель используется для представления знаний в системе логики предикатов первого порядка и выведения заключений с помощью силлогизма. Основное преимущество использования логики предикатов для представления знаний заключается в том, что обладающий хорошо понятными математическими свойствами мощный механизм вывода может быть непосредственно запрограммирован. С помощью этих программ из известных ранее знаний могут быть получены новые знания. Приведенные ниже примеры являются логическими моделями представления фактов с помощью предикатов и носят название атомарной формулы. ЛЮБОВЬ (Виктор, Ирина): Виктор любит Ирину СТОЛИЦА (Москва): Москва – столица Следующие примеры являются правильно построенными логическими формулами, включающими кванторы существования ( 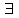 ) и общности ( ) и общности (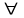 ). ).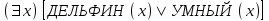 : некий дельфин наделен умственными способностями : некий дельфин наделен умственными способностями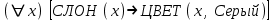 : все слоны имеют серую окраску : все слоны имеют серую окраскуОтличительными чертами логических моделей, в частности приведенных выше моделей представления знаний, являются единственность теоретического обоснования и возможность реализации системы формально точных определений и выводов. По этим причинам немало исследователей в области искусственного интеллекта выбрали для себя предметом изучения именно логические модели. Однако для логических моделей характерен ряд сомнительных моментов, а поскольку большинство исследователей в области искусственного интеллекта – люди с неформальным мышлением, то большая часть достижений в области систем с базами знаний до недавнего времени принадлежала так называемой группе исследователей нелогического направления. В отличие от исследователей логического направления, которые выбирают предметом своих исследований сравнительно простые задачи, для решения которых используются теоретические подходы, исследователи нелогического направления выбирают сложные задачи и пытаются сконцентрировать все внимание на развитии способностей. Кроме того, в отличие от первой категории исследователей, которые почти не занимаются теоретическими исследованиями, вторая категория придает им большое значение. Другими словами, так называемая “человеческая логика” – это интеллектуальная модель с нечеткой структурой – в этом ее отличие от строгой логики. Более точно следует сказать, что исследователи логического направления ищут пути логического решения (в малой модели) задач, поставленных исследователями нелогического направления, и постепенно расширяют рамки логики.. | ||||||||||||||||||
| | Лист | |||||||||||||||||
| 12 |
| | Лист |
| 13 |
Следовательно, такие системы не годятся для решения крупномасштабных задач. Упорядочим слабые и сильные стороны хорошо известных систем продукций. Сильные стороны:
Простота создания и понимания отдельных правил;
Простота пополнения, модификации и аннулирования;
Простота механизма логического вывода.
Слабые стороны:
Неясность взаимных отношений правил;
Сложность оценки целостного образа знаний;
Крайне низкая эффективность обработки;
Отличие от человеческой структуры знаний;
Отсутствие гибкости в логическом выводе.
Таким образом, если объектом является небольшая задача, выявляются только сильные стороны системы продукций. В случаях увеличения объема знаний, необходимости решения сложных задач, выполнения гибких выводов или повышения скорости вывода требуется структурирование базы данных. Первое, что приходит в голову в таких случаях, - это группировка знаний и структурирование базы данных. Другими словами, путем предварительной группировки соответствующих правил в некотором состоянии процесса вывода можно ограничить диапазон выбора правил. В тех случаях, когда объекты, для которых используются правила, также имеют иерархическую структуру, эффективным является структурирование базы данных. Этот подход был реализован в системах EMICIN и MECS-AI, разработанных на базе системы MYCIN с применением универсального языка представления знаний.
Расширенным вариантом модели правил является модель доски объявлений (blackboard), которая была предложена в системе распознавания разговорной речи HEARSAY-II как модель представления знаний.



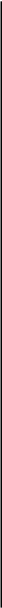
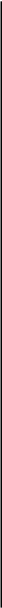

| | Лист |
| 14 |
1.3.3 Представление знаний фреймами
Фреймовая модель, или модель представления знаний, основанная на фреймовой теории М. Минского, представляет собой систематизированную модель памяти человека и его сознания.
Теория фреймов - это парадигма для представления знаний с целью использования этих знаний компьютером. Впервые была представлена Минским в 1975 году, как попытка построить фреймовую сеть, или парадигму с целью достижения большего эффекта понимания. С одной стороны, он пытался сконструировать базу данных, содержащую энциклопедические знания, но с другой стороны, хотел создать наиболее описывающую базу, содержащую информацию в структурированной и упорядоченной форме. Эта структура позволила бы компьютеру вводить информацию в более гибкой форме, имея доступ к тому разделу, который требуется в данный момент. Минский разработал такую схему, в которой информация содержится в специальных ячейках, называемых фреймами, объединенными в сеть, называемую системой фреймов. Новый фрейм активизируется с наступлением новой ситуации. Отличительной его чертой является то, что он одновременно содержит большой объем знаний и в то же время является достаточно гибким для того, чтобы быть использованным как отдельный элемент базы данных. Термин «фрейм» был наиболее популярен в середине семидесятых годов, когда существовало много его толкований, отличных от интерпретации Минского.
Итак, как было сказано выше фреймы – это фрагменты знания, предназначенные для представления стандартных ситуаций. Термин «фрейм» (Frame – рамка) был предложен Минским. Фреймы имеют вид структурированных компонентов ситуаций, называемых слотами. Слот может указывать на другой фрейм, устанавливая, таким образом, связь между двумя фреймами. Могут устанавливаться общие связи типа связи по общению [2].
Формальная структура фрейма имеет вид:
f [
Значение слота может быть представлено последовательностью
Каждый фрейм, как структура хранит знания о предметной области (фрейм–прототип), а при заполнении слотов знаниями превращается в конкретный фрейм события или явления.
Фреймы можно разделить на две группы: фреймы-описания; ролевые фреймы.
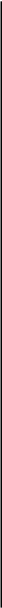


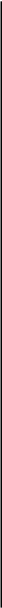

| | Лист |
| 15 |
Во фрейме-описании в качестве имен слотов задан вид программного обеспечения, а значение слота характеризует массу и производителя конкретного вида продукции. В ролевом фрейме в качестве имен слотов выступают вопросительные слова, ответы на которые являются значениями слотов. Для данного примера представлены уже описания конкретных фреймов, которые могут называться либо фреймами – примерами, либо фреймами – экземплярами. Если в приведенном примере убрать значения слотов, оставив только имена, то получим фрейм – прототип.
Достоинство фрейма – представления во многом основываются на включении в него предположений и ожиданий. Это достигается за счет присвоения по умолчанию слотам фрейма стандартных ситуаций. В процессе поиска решений эти значения могут быть заменены более достоверными. Некоторые переменные выделены таким образом, что об их значениях система должна спросить пользователя. Часть переменных определяется посредством встроенных процедур, называемых внутренними. По мере присвоения переменным определенных значений осуществляется вызов других процедур. Этот тип представления комбинирует декларативные и процедурные знания.
Фреймовые модели обеспечивают требования структурированности и связанности. Это достигается за счет свойств наследования и вложенности, которыми обладают фреймы, т.е. в качестве слотов может выступать система имен слотов более низкого уровня, а также слоты могут быть использованы как вызовы каких-либо процедур для выполнения.
Для многих предметных областей фреймовые модели являются основным способом формализации знаний.
