Курсовая работа по дисциплине Системы автоматизированного проектирования и конструирования измерительных приборов на тему Компенсационный акселерометр
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
|
Расчет элемента Дифференциальный трансформатор для измерения линейных перемещений (LVDT) представляет собой электромеханический преобразователь, который определяет механическое смещение сердечника и выдает пропорциональное переменное напряжение на выходе.[5] Рассмотрим конструкцию трансформаторного датчика угла, показанную на рис. 13. Датчик угла состоит из неподвижной части и подвижного ферромагнитного якоря 1. Основой неподвижной части является симметричный Ш-образный магнитопровод 2 из ферромагнитного материала с высокой магнитной проницаемостью. На центральном стержне магнитопровода находится обмотка возбуждения 3. На боковых стержнях магнитопровода расположены обмотки съема сигнала 4.  Рисунок 13. Конструкция трансформаторного датчика угла с переменной площадью сечения магнитопровода Обмотки съема сигнала включаются встречно-последовательно. Обмотка возбуждения создает магнитный поток, который замыкается через магнитопровод, немагнитные зазоры и подвижный якорь. Магнитные потоки, проходящие через боковые стержни магнитопровода, наводят в обмотках 4 ЭДС. При центральном положении якоря потоки, замыкающиеся через левую и правую часть магнитопровода, будут одинаковыми. При этом наводимые этими потоками в обмотках 4 ЭДС также будут одинаковыми.  Рисунок 14. Распределение магнитного потока обмотки возбуждения При повороте якоря, например, вправо, площадь, через которую магнитный поток проходит из левого стержня магнитопровода в якорь, уменьшится, а площадь, через которую магнитный поток проходит из правого стержня магнитопровода в якорь, наоборот, возрастет. Таким образом, магнитное сопротивление левой части магнитопровода увеличится, а правой – уменьшится. При изменении магнитного сопротивления магнитный поток перераспределяется – уменьшается в левой части и увеличивается в правой. Соответственно, изменяются и ЭДС, наводимые в обмотках 4. На рис. 15 показана другая возможная схема трансформаторного датчика угла.  Рисунок 15. Конструкция трансформаторного датчика угла с переменным воздушным зазором Датчик, конструкция которого показана на рис. 15, состоит из двух одинаковых П-образных магнитопроводов 2, каждый из которых содержит обмотку возбуждения 3 и обмотку съема сигнала 4. В среднем положении якоря воздушные зазоры между сердечником и якорем как в правой, так и в левой частях будут одинаковыми. Если левая и правая часть датчика имеют одинаковые конструктивные параметры, и питаются от одного и того - же источника напряжения, то наводимая в выходных обмотках 4 ЭДС будет одинаковой. При повороте якоря в одном сердечнике воздушные зазоры уменьшаются, а в другом – увеличиваются. Соответственно при уменьшении воздушных зазоров наводимая в выходной обмотке 4 ЭДС будет увеличиваться, а при увеличении воздушных зазоров – уменьшаться. Таким образом, разность ЭДС выходных обмоток будет определяться величиной угла поворота якоря. Если заданы основные конструктивные размеры магнитопровода, то порядок расчета трансформаторного датчика угла может быть следующим: Составление эскиза датчика с указанием размеров. Составление электрической схемы замещения магнитной цепи. Расчет магнитных проводимостей воздушных зазоров. Расчет магнитных проводимостей участков магнитопровода. Расчет допустимого магнитного потока и требуемой магнитодвижущей силы. Расчет зависимости магнитных потоков через обмотки съема сигнала в зависимости от угла поворота якоря. Расчет числа витков и диаметра провода обмотки возбуждения. Расчет числа витков и диаметра провода обмоток съема сигнала. Расчет статической характеристики датчика. Тепловой расчет обмотки возбуждения. Составление электрической схемы замещения магнитной цепи Электрическая схема замещения магнитной цепи представляет магнитную цепь в виде эквивалентной электрической цепи. К получившейся схеме применимы все методы расчета электрических цепей. При составлении схемы замещения магнитная цепь разбивается на участки, в пределах которых магнитный поток является постоянным и поперечное сечение которых также постоянно. Если пренебречь потоками рассеяния магнитопровода и обмоток, то расчет магнитной цепи датчика, показанного на рис. 13, можно провести на основе схемы замещения, показанной на рис. 16.  Рисунок 16. Схема замещения магнитной цепи для датчика на рис.13 Схема замещения включает в себя источник создаваемой обмоткой возбуждения магнитодвижущей силы  , комплексные магнитные сопротивления магнитопровода (левой и правой частей основания - , комплексные магнитные сопротивления магнитопровода (левой и правой частей основания -  , центрального стержня - , центрального стержня -  , боковых стрежней - , боковых стрежней -  ), комплексные магнитные сопротивления якоря ( ), комплексные магнитные сопротивления якоря (  ) и магнитные сопротивления воздушных зазоров (между центральным стержнем и якорем - ) и магнитные сопротивления воздушных зазоров (между центральным стержнем и якорем -  , между левым стержнем и якорем - , между левым стержнем и якорем -  , между правым стержнем и якорем - , между правым стержнем и якорем -  ). ).Отметим, что потоком рассеяния при приближенных инженерных расчетах можно пренебречь в двух случаях: когда магнитопровод замкнут; когда на пути основного магнитного потока имеется воздушный зазор сравнительно малой величины, а магнитная цепь насыщена незначительно. Расчет магнитных проводимостей воздушных зазоров Магнитное сопротивление воздушного зазора  является активным. Оно практически не зависит от величины магнитной индукции в зазоре и частоты ее изменения (частоты напряжения питания обмотки возбуждения). является активным. Оно практически не зависит от величины магнитной индукции в зазоре и частоты ее изменения (частоты напряжения питания обмотки возбуждения).При расчетах удобнее определять величину, обратную магнитному сопротивлению - магнитную проводимость:  Магнитная проводимость определяется геометрическими характеристиками воздушного зазора. Для рис. 12 конфигурация воздушных зазоров является криволинейной и достаточно сложной для расчета. Для упрощения расчета приведем криволинейные поверхности к эквивалентным прямолинейным. В этом случае для проводимости  расчетная схема будет иметь вид, показанный на рис. 17. расчетная схема будет иметь вид, показанный на рис. 17. Рисунок 17. К расчету проводимости воздушного зазора Значение эквивалентной ширины центрального стержня сердечника с определяется из геометрических построений (значение функции arcsin следует вычислять в радианах):  где  радиус кривизны торцевой части центрального стержня сердечника (см. рис. 13); a – половина ширины центрального стержня сердечника (см. рис. 13). радиус кривизны торцевой части центрального стержня сердечника (см. рис. 13); a – половина ширины центрального стержня сердечника (см. рис. 13).Согласно рис. 13 и условию задания радиус кривизны торцевой части центрального стержня сердечника будет следующим:  где  наружний радиус якоря, равный 15 мм, а наружний радиус якоря, равный 15 мм, а  воздушный зазор между якорем и сердечником. воздушный зазор между якорем и сердечником. Тогда, согласно формуле (1) эквивалентная ширина центрального стержня сердечника с будет равна:  В соответствии с рис. 15 магнитная проводимость воздушного зазора  может быть определена по формуле [П.В. Сахаров]: может быть определена по формуле [П.В. Сахаров]: где  - абсолютная магнитная проницаемость вакуума, - абсолютная магнитная проницаемость вакуума,  удельные проводимости, которые характеризуют проводимость поля выпучивания между соответствующим ребром сердечника и торцевой поверхностью якоря; удельные проводимости, которые характеризуют проводимость поля выпучивания между соответствующим ребром сердечника и торцевой поверхностью якоря;  характеризуют проводимость между боковой поверхностью сердечника и торцевой поверхностью якоря. характеризуют проводимость между боковой поверхностью сердечника и торцевой поверхностью якоря.Величины  определяются по номограмме, показанной на рис. 18. Величины определяются по номограмме, показанной на рис. 18. Величины  определяются по монограммам рис. 19 и рис. 20 [П.В. Сахаров]. определяются по монограммам рис. 19 и рис. 20 [П.В. Сахаров]. Рисунок 18. Кривая удельной магнитной проводимости «ребро-торец» в зависимости от отношения размера сердечника к воздушному зазору Для нахождения величин  по рис. 17 рассчитаем отношения по рис. 17 рассчитаем отношения  воздушный зазор между якорем и сердечником, равный 0,0002 м: воздушный зазор между якорем и сердечником, равный 0,0002 м:  Сопоставляя полученные данные с рис. 6 можно сделать вывод, что  По рис. 20 нам необходимо определить отношения  , для чего требуется определить параметры x иy. , для чего требуется определить параметры x иy.Величина x – это расстояние от края бокового стержня до той части стержня, которую покрывает якорь (выделено на рис. 19), а y – зазор между центральным стержнем и контуром якоря (выделено на рис. 19).  Рисунок 19. Определение велечин xиy По рис. 19 x = 2 мм, y = 0,5 мм, тогда:    Согласно полученным результатам по рис. 20 определяем отношения величин  : : Рисунок 20. График соотношения между координатами потоков выпучивания По рис. 20 наглядно видно, что  По рис. 21 определим величины   Рисунок 21. Кривые удельной боковой магнитной проводимости в зависимости от отношения  Согласно рис. 21  (т.к. (т.к. ). ).Тогда, согласно всем полученным данным мы можем рассчитать по формуле (2) магнитную проводимость воздушного зазора   Расчет проводимостей воздушных зазоров 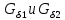 более сложен, особенно при учете того, что картина магнитного поля выпучивания будет изменяться при повороте якоря. Упрощенная расчетная схема для определения проводимости более сложен, особенно при учете того, что картина магнитного поля выпучивания будет изменяться при повороте якоря. Упрощенная расчетная схема для определения проводимости 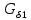 при начальном положении якоря показана на рис. 22. при начальном положении якоря показана на рис. 22.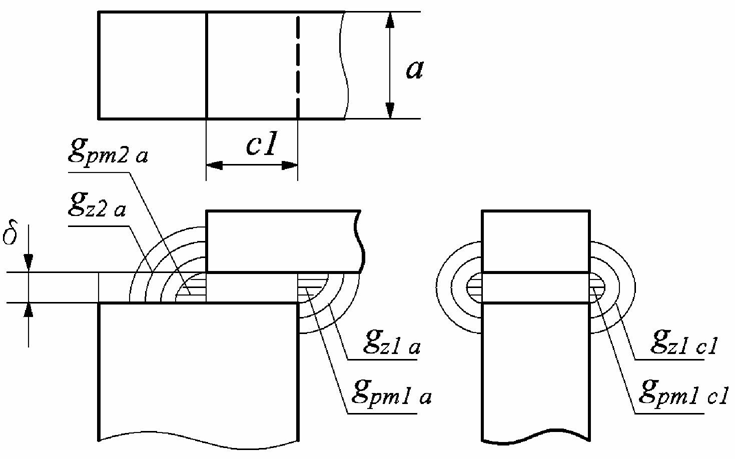 Рисунок 22. К расчету проводимости воздушного зазора Для дальнейшего упрощения расчетов примем, что 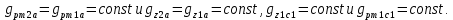 В этом случае проводимости боковых зазоров можно определить по формуле: В этом случае проводимости боковых зазоров можно определить по формуле: 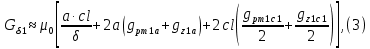 где 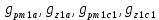 определяются по номограммам на рис. 16 – рис. 22. определяются по номограммам на рис. 16 – рис. 22.Размер clопределяется по эскизу датчика и формуле, аналогичной (1): 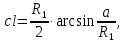 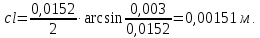 Учитывая изменение зазоров при повороте якоря, для проводимостей можно записать:   где dc – изменение размера перекрытия сердечника и якоря при повороте якоря:  где  величина угла поворота якоря датчика в радианах. величина угла поворота якоря датчика в радианах.Найдем угол при помощи рис. 13, рис. 23 и рис .24. Согласно рис. 13 нам следует находить угол из двух треугольников: первый треугольник – начальное положение якоря, второе – смещение якоря на угол 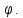 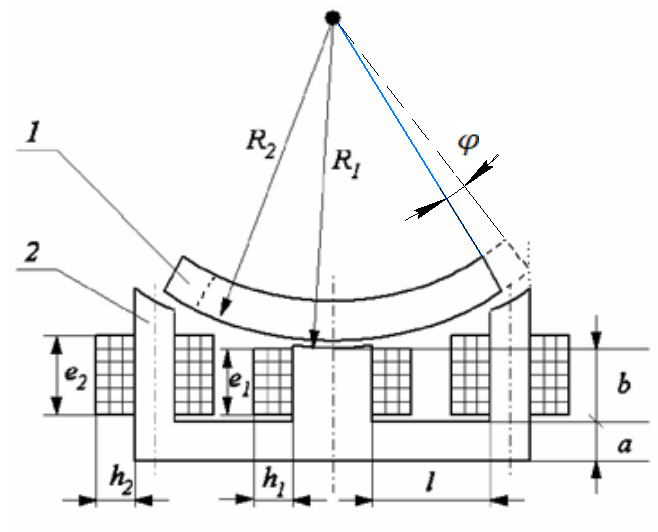 Рисунок 23. Смещение якоря на угол 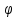 На рис. 23 на основе рис. 13 сплошной линей показано начальное положение якоря, а пунктирной линией – перемещение якоря на угол 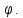 Тогда, согласно рис. 23 можно получить два треугольника, изображенные на рис. 24 и при помощи которых находим угол Тогда, согласно рис. 23 можно получить два треугольника, изображенные на рис. 24 и при помощи которых находим угол   Рисунок 24. Треугольники, полученные при перемещении якоря Начнем расчет сторон треугольника. Треугольник первый (начальное положение якоря):    Тогда угол  будет равен: будет равен: Аналогичным способом делаем вычисления для второго треугольника (когда якорь смещен):    Тогда угол  будет равен: будет равен: Тогда, зная начальный угол и угол смещенного маятника, мы можем найти угол перемежения:  По формуле (5) рассчитаем изменение размера перекрытия сердечника и якоря при повороте якоря:  При сопоставлении рис. 17 и рис. 22 можно сказать, что:  ; ;   Теперь можем по формуле (4) рассчитать проводимости:   Расчет магнитных проводимостей участков магнитопровода Магнитное сопротивление  участка ферромагнитного магнитопровода в общем случае является комплексной величиной: участка ферромагнитного магнитопровода в общем случае является комплексной величиной: где:  – активное магнитное сопротивление участка сердечника, – активное магнитное сопротивление участка сердечника,   – реактивная составляющая магнитного сопротивления, обусловленная вихревыми токами и потерями на гистерезис, – реактивная составляющая магнитного сопротивления, обусловленная вихревыми токами и потерями на гистерезис,  ; ;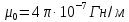 – абсолютная магнитная проницаемость вакуума; – абсолютная магнитная проницаемость вакуума;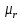 – относительная магнитная проницаемость; – относительная магнитная проницаемость;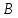 –магнитная индукция в пределах участка магнитопровода; –магнитная индукция в пределах участка магнитопровода;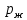 – удельные потери в материале магнитопровода, – удельные потери в материале магнитопровода,  обусловленные вихревыми токами и гистерезисом; обусловленные вихревыми токами и гистерезисом; – масса участка магнитопровода, кг; – масса участка магнитопровода, кг; – длина участка магнитопровода, м; – длина участка магнитопровода, м; –поперечное сечение участка магнитопровода, –поперечное сечение участка магнитопровода,  ; ; – круговая частота напряжения питания обмотки возбуждения; – круговая частота напряжения питания обмотки возбуждения;Учитывая, что  приведем формулу (7) к виду: приведем формулу (7) к виду: Величина удельных потерь мощности на гистерезис и вихревые токи  зависит от частоты и магнитной индукции [П.В. Сахаров]: зависит от частоты и магнитной индукции [П.В. Сахаров]: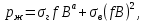 где: 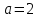 при B=1,0…1,9 Тл; при B=1,0…1,9 Тл; 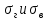 – опытные коэффициенты, равные – опытные коэффициенты, равные 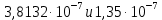 соответственно. соответственно.Тогда: 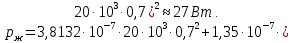 Таким образом, формула (8) приводится к виду: 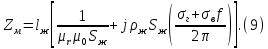 В общем случае величина 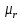 зависит от магнитной индукции B и напряженности магнитного поля H, взаимосвязь между которыми зависит от магнитной индукции B и напряженности магнитного поля H, взаимосвязь между которыми 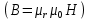 определяется кривыми намагничивания или кривыми гистерезиса. определяется кривыми намагничивания или кривыми гистерезиса.В тоже время для каждого вида материала имеется достаточно широкая область значений магнитной индукции, в пределах которой  можно считать постоянной. Для большинства магнитомягких материалов диапазон магнитной индукции, в пределах которого магнитное сопротивление не изменяется [Сахаров П.В.], можно принять равным B=0,3…1,2 Тл. Учитывая, что при перемещении якоря магнитная индукция в боковых частях сердечника будет изменяться, примем B=0,7 Тл. можно считать постоянной. Для большинства магнитомягких материалов диапазон магнитной индукции, в пределах которого магнитное сопротивление не изменяется [Сахаров П.В.], можно принять равным B=0,3…1,2 Тл. Учитывая, что при перемещении якоря магнитная индукция в боковых частях сердечника будет изменяться, примем B=0,7 Тл.Для наших расчетов возьмем феррит 2000НМ1, относительная магнитная проницаемость которого  . Тогда напряженность магнитного поля будет равна: . Тогда напряженность магнитного поля будет равна:  В целях упрощения расчетов исключим из формулы (9) комплексную составляющую и будем рассчитывать магнитные сопротивления участков по следующей формуле:  Как следует из рис. 13 и рис. 16, Ш-образная часть магнитопровода разбивается на пять участков. В местах сопряжения участков магнитопровода их длину можно определять по-разному, при этом необходимо следить, чтобы одна и та же часть магнитопровода не вошла в различные участки. Возможные варианты разбиения магнитопровода на части показаны на рис. 25.  Рисунок 25. Возможные способы разбиения магнитопровода на участки Будем рассчитывать сопротивления по первому варианту, указанному на рис. 25. Тогда, согласно рис. 16 и рис. 25 по формуле (10) можно рассчитать сопротивления 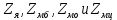 , которые соответствуют сопротивлению якоря, сопротивлению боковых стержней, сопротивлению участка магнитопровода между боковыми стержнями и центральным и сопротивлению центрального стержня соответственно. , которые соответствуют сопротивлению якоря, сопротивлению боковых стержней, сопротивлению участка магнитопровода между боковыми стержнями и центральным и сопротивлению центрального стержня соответственно.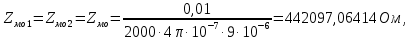 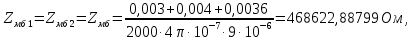 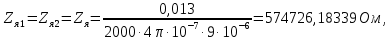  где индексы 1 и 2 указывают на левую и правую часть рассчитываемого участка. Расчет числа витков обмотки возбуждения Число витков обмотки возбуждения определяется исходя из допустимого тока в данной обмотке и максимальной величины магнитной индукции в магнитопроводе. Величина тока  в обмотке возбуждения (при ненагруженных обмотках съема сигнала) определяется напряжением питания и индуктивностью обмотки: в обмотке возбуждения (при ненагруженных обмотках съема сигнала) определяется напряжением питания и индуктивностью обмотки: где  омическое сопротивление обмотки возбуждения; омическое сопротивление обмотки возбуждения; 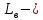 индуктивность обмотки возбуждения; индуктивность обмотки возбуждения; 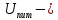 напряжение питания обмотки возбуждения. напряжение питания обмотки возбуждения.Индуктивность определяется числом витков обмотки и магнитным сопротивлением датчика: 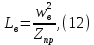 где  приведенное магнитное сопротивление; приведенное магнитное сопротивление; 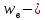 число витков обмотки возбуждения. число витков обмотки возбуждения.На основе схемы замещения, показанной на рис. 15, найдем:  где, согласно определению магнитной проводимости, магнитное сопротивление будет определяться как:  Тогда:   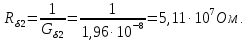 Согласно полученным расчетам, посчитаем приведенное магнитное сопротивление 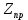 по формуле (13): по формуле (13): 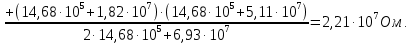 Для оценки требуемого числа витков в первом приближении можно считать, что ток ограничивается только индуктивным сопротивлением обмотки. В этом случае упрощая формулу (21) и учитывая (22) получим выражение для определения требуемого числа витков: 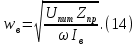 Током 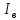 задаются. Как правило, для датчиков значения тока выбираются по возможности малыми с целью уменьшения моментов электромагнитного тяжения и влияния гистерезиса. Как правило, величину тока возбуждения принимают в диапазоне 1...10 мА. Приняв задаются. Как правило, для датчиков значения тока выбираются по возможности малыми с целью уменьшения моментов электромагнитного тяжения и влияния гистерезиса. Как правило, величину тока возбуждения принимают в диапазоне 1...10 мА. Приняв 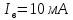 , посчитаем число витков по формуле (14): , посчитаем число витков по формуле (14):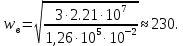 Определим индуктивность по формуле (12): 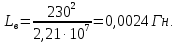 После определения числа витков по формуле (14) проводится проверочный расчет на превышение допустимого значения магнитной индукции. Для этого определяется магнитный поток в центральном стержне по формуле: 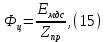 где 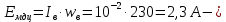 магнитодвижущая сила. Тогда: магнитодвижущая сила. Тогда: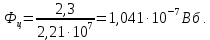 По величине магнитного потока и сечению стержня определяется значение магнитной индукции: 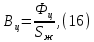  Значение индукции  не должно превышать значения, допустимого для выбранного материала сердечника и якоря. Как правило, значение магнитной индукции не должно превышать не должно превышать значения, допустимого для выбранного материала сердечника и якоря. Как правило, значение магнитной индукции не должно превышать  Если полученное по формуле (16) значение магнитной индукции превышает допустимую величину, то число витков рассчитывается по формулам (15) и (16). Затем, на основании формул (11) – (14) определяется ток первичной обмотки. В нашем случае значение магнитной индукции не превышает допустимую величину. В соответствии с законами Кирхгофа:  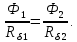 Таким образом, получим: 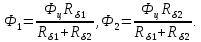 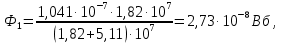 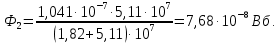  Величина напряжения питания индуктивного датчика ограничивается двумя факторами: Допустимой температурой перегрева датчика:  где:  максимальная допускаемая температура датчика; максимальная допускаемая температура датчика; максимальная температура окружающей среды; максимальная температура окружающей среды;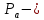 активная мощность, выделяемая в датчике; активная мощность, выделяемая в датчике;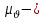 коэффициент теплоотдачи (0,1…0,2 коэффициент теплоотдачи (0,1…0,2 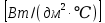 ); );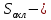 поверхность охлаждения датчика. поверхность охлаждения датчика.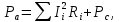 где 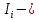 ток i-ой обмотки датчика, ток i-ой обмотки датчика, 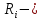 активное сопротивление i-ой обмотки датчика, активное сопротивление i-ой обмотки датчика, 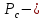 мощность потерь в сердечнике. мощность потерь в сердечнике.Для одиночной обмотки: 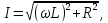 где 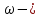 частота питающего напряжения, частота питающего напряжения, 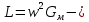 индуктивность обмотки, индуктивность обмотки, 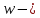 число витков обмотки, число витков обмотки, 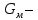 магнитная проводимость магнитопровода. магнитная проводимость магнитопровода.Допустимой величиной магнитной индукции 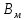 в металлическом магнитопроводе датчика: в металлическом магнитопроводе датчика: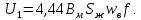 Индуктивность электромагнитной системы L определяется отношением числа потокосцеплений к вызвавшему их току I: 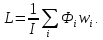 В системах, содержащих обмотку и ферромагнитный сердечник с небольшим воздушным зазором рассеянием магнитного потока можно пренебречь:  3.Разработка чертежа Современные графические средства разрабатываются с таким расчетом, чтобы не только дать удобные инструменты профессиональным художникам и дизайнерам, но и предоставить возможность для продуктивной деятельности тем, кто не имеет необходимых профессиональных навыков и врожденных способностей к художественному творчеству. В настоящее время наибольшую популярность имеют две программы: «Компас-3D» и «SolidWorks». Первый редактор имеет широкую популярность в студенческой среде из-за своей простоты и понятности; другое приложение приобрело свою известность благодаря массовому использованию на оборонных предприятиях страны, оно обладает обширным функционалом, позволяющим специалистам быстро и точно выполнять свою работу. Набор основных инструментов формообразования при твердотельном моделировании Сравнение начну с инструментов твердотельного моделирования, которые помогают подготовить детали для токарной и фрезерной обработки. Набор таких инструментов в обеих САПР богат и сопоставим. Отличия присутствуют в параметрах выполнения операций. Например, SolidWorks позволяет выполнять операцию добавления материала выдавливанием не только от плоскости эскиза, но и от другой плоскости, поверхности или даже вершины. КОМПАС-3D располагает таким функционалом только в конечном направлении операции выдавить: на расстояние, через все, до вершины, до поверхности или до ближайшей поверхности. Однако, он позволяет сделать элемент тонкостенным в любой момент проектирования, изменив параметры при редактировании операции. А SolidWorks, в свою очередь, позволяет сделать элемент тонкостенным только в момент создания операции. Таким образом, чтобы элемент со сплошным телом стал тонкостенным, операцию необходимо удалить и выполнить заново. Теперь несколько слов об операциях для формообразования деталей, получаемых перемещением эскиза вдоль другого эскиза. В российской САПР для этого имеется «Кинематическая» команда, а в SolidWorks - «По траектории». Если траектория выходит за рамки плоскости, то КОМПАС-3D предоставляет инструменты пространственных кривых, а в SolidWorks для этих целей удобно пользоваться 3D-эскизом. Подходы в принципе разные, но обеспечивают конструкторов сопоставимыми возможностями и позволяют достичь равных результатов. Работа с деталями различных исполнений Если детали или сборочные единицы обладают общими конструктивными элементами, имея при этом незначительные различия между собой, то согласно ГОСТ 2.113-75 при оформлении документации на них эти различия можно отразить в исполнениях детали или сборочной единицы, оформив на них общие конструкторские документы. SolidWorks позволяет отразить незначительные изменения в конфигурациях деталей и сборочных единиц. Доступ к конфигурациям осуществляется через вкладку дерева документа «Конфигурации». В КОМПАС-3D есть специальная команда создания исполнения детали или сборочной единицы, которая соответствует логике ГОСТ 2.113-75. Различные исполнения модели доступны из менеджера документа или из контекстного меню выбора текущего исполнения. Важным аспектом является то, что при оформлении чертежей и спецификаций в КОМПАС-3D передача информации об исполнениях из моделей в эти документы также происходит в полном соответствии с требованиями всё того же стандарта. Исполнения появились в КОМПАС-3D с 15-й версии. Их отсутствие в более ранних версиях пользователи часто ставили в упрек системе, указывая на наличие упомянутых конфигураций в SolidWorks. Однако и ранее можно было получить нечто, напоминающее конфигурации одного изделия, с помощью внешних переменных и аналитических взаимосвязей между внешними переменными нескольких деталей и сборочных единиц. При этом вся информация об отличиях хранилась в таблице переменных. Доступ к разным конфигурациям детали или сборочной единицы также реализовывался через неё. Инструменты для реализации методик нисходящего и восходящего проектирования в САПР Сегодня принято выделять несколько основных методик проектирования: нисходящее проектирование (сверху вниз) восходящее проектирование (снизу вверх). В их основе заложены принципы решения задач от общего к частному или от частного к общему. Возможно и сочетание двух принципов в равной мере в зависимости от значимости проектируемой детали в сборочной единице в целом. Обе методики могут быть использованы при проектировании в обеих рассматриваемых САПР. В качестве примера нисходящего проектирования (сверху вниз) приведу модель, которая была создана на основании имеющихся в наличии комплектующих для небольшого ЧПУ-станка. На ее основе формировались детали и сборочные единицы - элементы несущих конструкций. |
