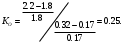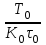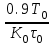Курсовая работа по дисциплине Теория автоматического управления Расчет оптимальных настроек непрерывных и дискретных регуляторов
 Скачать 0.66 Mb.
|
3 Расчет передаточной функции по кривой откликаКривая отклика - реакция системы на частичное ступенчатое изменение управляющего воздействия. Алгоритм получения кривой отклика предполагает, что длительное время объект работал на некотором установившемся режиме. В момент времени t0 управляющее воздействие изменилось скачком на некоторую величину (процент открытия клапана, объем подачи жидкости, газа), за которым последовало изменение выходной величины, например как на рисунке 1, где реакция имеет монотонный характер и некоторое запаздывание. В этом случае возможно представление передаточной функции в виде последовательного соединения апериодического звена и звена чистого запаздывания: 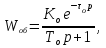 (1)где Ко – коэффициент передачи объекта; τо– постоянная времени запаздывания объекта; То – постоянная времени объекта. Свойства апериодического звена позволяют вычислить параметры объекта К0 ; Т0; τо, используя метод касательной. Для этого строится касательная с наибольшим наклоном к кривой отклика, определяется момент времени (t1) ее пересечения с осью абсцисс (Х0) и (t2) с линией нового установившегося значения (Х1), где исходное установившееся значение Х0 и новое установившееся значение Х1, исходное значение управляющего воздействия U0 и новое управляющее воздействие U1, которое появилось в момент времени (t0) (рисунок 3). 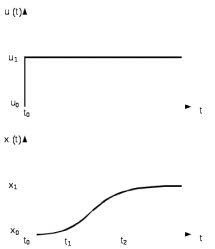 Рисунок 3 – Определение характеристик объекта на графике кривой отклика Расчет параметров объекта выполняется по формулам: 0 = t1-t0; (2) Т0 = t2 - t1, (3) 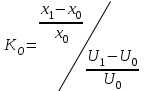 . (4)Если управляющее воздействие задается в процентах, то в формуле в знаменателе вместо U0 записывается 100.
4 Метод Зиглера-НикольсаМетоды Зиглера-Никольса и Коэна-Куна относятся к эмпирическим методам, формулы для расчета настроек подбирались при определенной скорости затухания переходных процессов, равной четырем, поэтому настройки для некоторых объектов могут быть далеки от оптимальных, особенно временные настройки (Ти и Тд). Алгоритм расчета настроек регуляторов для объекта, заданного кривой отклика имеет ряд шагов: выбор формы передаточной функции объекта; выбор метода определения параметров объекта; выбор типа регулятора; расчет настроек регулятора; проверка оптимальности настроек расчетом прямых (косвенных) показателей качества и сравнения с допустимыми значениями. Выбор типа регулятора для конкретного объекта выполняется с учетом свойств объекта. Одной из рекомендаций является вычисление отношения 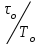 . Соответствие между числовыми значениями и типами регуляторов приведены в таблице 2.Таблица 2 – Соответствие между 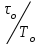и типом регулятора
Расчет настроек по методу Зиглера-Никольса выполняется согласно таблицы 3. Таблица 3 – Настройки регуляторов по методу Зиглера – Никольса
| ||||||||||||||||||||||||||||||||||||||||||
