Курсовая работа по дисциплине Теория автоматического управления Расчет оптимальных настроек непрерывных и дискретных регуляторов
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
6 Расчет настроек дискретного ПИ-регулятора методом ограничения на частотный показатель колебательностиДля исключения статической ошибки в контурах регулирования используется интегральное звено, часто оно входит в состав регулятора. Тогда возможно использование для расчета настроек регулятора метода ограничения на частотный показатель колебательности. Частотный показатель колебательности относится к косвенным показателям качества и определяется по АЧХ замкнутой системы: 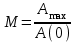 . (6) . (6)Значение этого показателя косвенно связано с запасом устойчивости, а также с прямыми показателями качества (перерегулированием и временем регулирования). Если в системе присутствует интегральное звено, то значение амплитудно-частотной характеристики при нулевой частоте равно единице (А(0)=1), при этом значение частотного показателя колебательности определяется максимальным значением АЧХ, т.е. М=Аmax. Тогда линии равных значений M на комплексной плоскости имеют вид окружности (приложение Б), параметры (радиус и центр) которой рассчитываются по формулам: 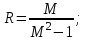 (7) (7)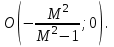 (8) (8)В каждой точке окружности имеет место определенный запас устойчивости, соответствующий этому значению М, поэтому если АФЧХ разомкнутой системы касается окружности (рисунок 10), то параметры регулятора обеспечивают этот запас устойчивости [4]. 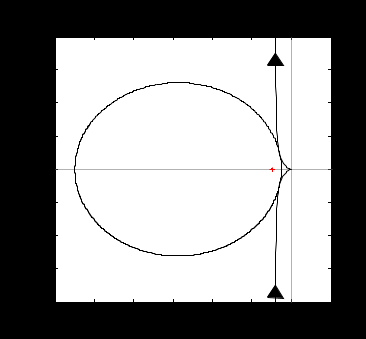 Рисунок 10 – Пример АФЧХ разомкнутой системы, касающейся окружности Если АФЧХ находится вне окружности и не касается ее (рисунок 11), то запас устойчивости больше, чем в точках окружности. 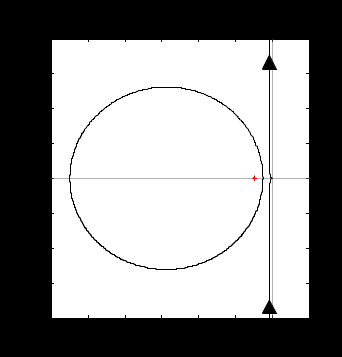 Рисунок 11 – Пример АФЧХ разомкнутой системы, не касающейся окружности Если АФЧХ заходит в окружность (рисунок 12), то запас устойчивости становится меньше, и при определенных значениях параметров замкнутая система может стать неустойчивой. 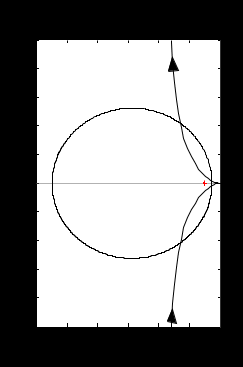 Рисунок 12 – Пример АФЧХ разомкнутой системы, пересекающей окружность Поэтому алгоритм метода предполагает следующие шаги: выбор допустимого значения частотного показателя колебательности (Мдоп); расчет параметров окружности (радиуса R и центра O) и построение ее на комплексной плоскости; выбор типа регулятора с учетом того, что в разомкнутой цепи должно быть интегральное звено (передаточные функции дискретных регуляторов приведены в приложении А); построение АФЧХ разомкнутой системы в общем виде; выбор интервала варьирования постоянной времени интегрирования Ти; выбор одного из значений Тии подбор коэффициента передачи регулятора Кр, обеспечивающего касание АФЧХ и окружности; повторение подбора Кр для других значений Ти; выбор в качестве оптимальных настроек значения той пары Кр и Ти, которые соответствуют наибольшему отношению Кр/Ти (по интегральному показателю качества управления приложение В); проверка косвенных и прямых показателей качества в контуре с найденными настройками. Если косвенные и прямые показатели качества оказались не хуже значений, допустимых по технологии, настройки считаются оптимальными. Если прямые показатели оказались несколько хуже допустимых, то можно на 10-20% изменить настройки, чтобы улучшить показатели. 6.1 Выбор допустимого значения частотного показателя колебательностиВыбор допустимого значения частотного показателя колебательности выполняется по номограмма Солодовникова (рисунок 13,14,15). В примере показано для перерегулирования, равного 30%. 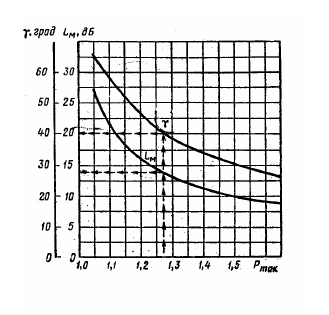 Рисунок 13 - График для определения Pmax и частоты среза по заданному перерегулированию 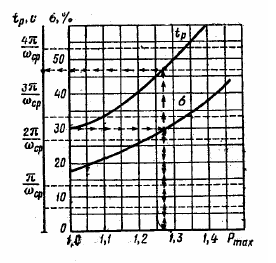 Рисунок 14- График для определения запаса по амплитуде и запаса по фазе 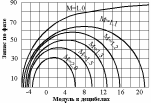 Рисунок 15 – График для определения значения частотного показателя Сделать расчет для перерегулирования, равного 25%. Мдоп =…… . |
