Одинцова - ТЭМП-1. Курсовая работа по дисциплине Теория электрометаллургических процессов Студент мцб121 Одинцова К. А
 Скачать 143.25 Kb. Скачать 143.25 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра металлургии цветных металлов ДОПУСКАЮ Руководитель _______ Кузьмина М.Ю. подпись инициалы, фамилия Построение диаграммы Пурбе для системы свинец-вода КУРСОВАЯ РАБОТА по дисциплине «Теория электрометаллургических процессов» Студент МЦб-12-1 _____________ Одинцова К.А. группа подпись инициалы, фамилия Курсовая работа защищена с оценкой ____________________________ Иркутск 2015 г. Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ По дисциплине «Теория электрометаллургических процессов» Студенту Одинцова К.А. Тема ___Построение диаграммы Пурбе для системы свинец-вода___ Исходные данные Расчет и постоение диаграммы Пурбе для системы свинец-вода при наличии фаз: 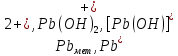 Рекомендуемая литература 1. Жучков И.А. Основы теории электрометаллургических процессов: учеб. пособие / И.А. Жучков. – Иркутск: Изд-во ИрГТУ, 2000. – 107 стр. 2. Антропов Л.И. Теоретическая электрохимия: Учеб. для хим.-технолог. спец. вузов. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1984. – 519 с. Дата выдачи задания “____” _______________20__ г. Дата представления работы руководителю “____” _________20__ г. Руководитель курсовой работы ___________________________________ (подпись, ФИО) Содержание Задание на курсовую работу 2 Введение 4 Методика построения диаграмм Пурбе 7 Диаграмма Пурбе для системы свинец-вода 10 Заключение 11 Список использованных источников 12 Введение Все химические процессы, как правило, обратимы. При протекании обратимой химической реакции пА + тВ↔ rG + qD по закону действующих масс скорость процесса в прямом направлении (слева направо) определяется как W1 = К1 · 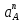 · ·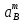 , а в обратном направлении (справа налево) – как W2 = К2 · , а в обратном направлении (справа налево) – как W2 = К2 ·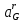 · ·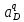 .. В этих выражениях, .. В этих выражениях,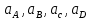 - активности соответствующих компонентов (А, В, G, D). Показатели степени п, т, r,q (стехиометрические коэффициенты при соответствующих членах реакции) называютсяпорядком реакции по данному компоненту. Коэффициенты пропорциональностиK1 и К2 имеют названиеконстант скорости реакции в соответственно в прямом и в обратном направлениях. Константа скорости реакции численно равна скорости реакции при единичных концентрациях реагирующих компонентов. Отношение К1/К2 - Кр называется "константой равновесия" химического процесса. - активности соответствующих компонентов (А, В, G, D). Показатели степени п, т, r,q (стехиометрические коэффициенты при соответствующих членах реакции) называютсяпорядком реакции по данному компоненту. Коэффициенты пропорциональностиK1 и К2 имеют названиеконстант скорости реакции в соответственно в прямом и в обратном направлениях. Константа скорости реакции численно равна скорости реакции при единичных концентрациях реагирующих компонентов. Отношение К1/К2 - Кр называется "константой равновесия" химического процесса.В момент равновесия скорости реакции в прямом и в обратном направлениях уравниваются: W1 = К1 · 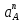 · ·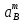 = W2 = К2 · = W2 = К2 ·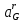 · ·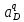 . Отсюда можно определить значение константы равновесия химического процесса: Кр = К1/К2 = . Отсюда можно определить значение константы равновесия химического процесса: Кр = К1/К2 = 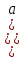 · ·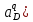 / /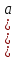 · ·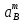 ), которое может быть найдено и расчетным путем по известным выражениям термодинамических функций веществ, участвующих в реакции: по изменению энергии ГиббсаΔG°, теплосодержания (энтальпии)ΔН° и энтропииΔS0. Изменение энергии Гиббса рассчитывается с учетом схемы процесса и табличных значений изобарно-изотермического потенциала участников реакции. Например, при электролизе сернокислого цинка на катоде протекает процесс восстановления ионов цинка:Zn2+ + 2е = Zn°, а на аноде - окисление кислорода воды: Н2О – 2е = 2Н+ +1/2О2. Поэтому суммарный окислительно - восстановительный процесс выражается следующей реакцией:Zn2+ + Н2О = Zn° + + 2Н++1/2О2. ), которое может быть найдено и расчетным путем по известным выражениям термодинамических функций веществ, участвующих в реакции: по изменению энергии ГиббсаΔG°, теплосодержания (энтальпии)ΔН° и энтропииΔS0. Изменение энергии Гиббса рассчитывается с учетом схемы процесса и табличных значений изобарно-изотермического потенциала участников реакции. Например, при электролизе сернокислого цинка на катоде протекает процесс восстановления ионов цинка:Zn2+ + 2е = Zn°, а на аноде - окисление кислорода воды: Н2О – 2е = 2Н+ +1/2О2. Поэтому суммарный окислительно - восстановительный процесс выражается следующей реакцией:Zn2+ + Н2О = Zn° + + 2Н++1/2О2.Изменение энергии Гиббса этого процесса при стандартной температуре составляет 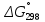 = – = – 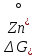 – – 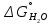 = – ( –147) – (– 237) = 384 кДж/моль. = – ( –147) – (– 237) = 384 кДж/моль.Изменение энергии Гиббса с изменением энтальпии и энтропии связано уравнением Гиббса - Гельмгольца:ΔGT = ΔНТ – T.ΔST . ЗначениеΔGTможет быть рассчитано, если известны стандартные величины 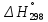 и и 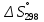 и зависимости изменения теплоемкостей реагирующих веществ от температуры. Отметим, что теплоемкость при постоянном объеме системы (Cv) или постоянном давлении (Ср) – это количество теплаdQ, которое надо передать единице вещества (грамму, грамм-молю), чтобы его температура поднялась на один градус: С(v, p) =dQ/dT. Изменение энтальпии и энтропии с изменением температуры имеет вид: и зависимости изменения теплоемкостей реагирующих веществ от температуры. Отметим, что теплоемкость при постоянном объеме системы (Cv) или постоянном давлении (Ср) – это количество теплаdQ, которое надо передать единице вещества (грамму, грамм-молю), чтобы его температура поднялась на один градус: С(v, p) =dQ/dT. Изменение энтальпии и энтропии с изменением температуры имеет вид: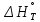 = = 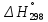 + + 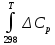 . dT и . dT и 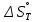 = = 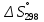 + + 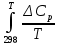 . dT. Поэтому . dT. Поэтому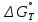 = = 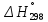 – T. ΔS298 – – T. ΔS298 –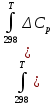 . dT) . . dT) . 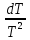 . Последний член этого уравнения представляет собой поправку на отклонение . Последний член этого уравнения представляет собой поправку на отклонение 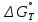 и и 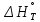 от стандартных значений. Рассчитанные величины этих поправок можно взять из специальных таблиц, предложенных М. М. Темкиным и Л. А. Шварцманом. Эти таблицы есть во многих изданиях по физической химии. от стандартных значений. Рассчитанные величины этих поправок можно взять из специальных таблиц, предложенных М. М. Темкиным и Л. А. Шварцманом. Эти таблицы есть во многих изданиях по физической химии.Связь между константой равновесия Кр и энергией Гиббса 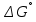 при температуре Т выражается соотношением при температуре Т выражается соотношением 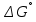 = –2,3RT. lg(Kp). Отсюда для рассматриваемого процесса значение логарифма константы равновесия при температуре 20 °С (293К) составляетlg(Kp)= = –2,3RT. lg(Kp). Отсюда для рассматриваемого процесса значение логарифма константы равновесия при температуре 20 °С (293К) составляетlg(Kp)= 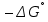 /(2,3RT ) = – 384000/(2,3 . 8,314 . 293) = – 68,5. Следовательно, Кр = 10–68,5. При больших отрицательных значениях /(2,3RT ) = – 384000/(2,3 . 8,314 . 293) = – 68,5. Следовательно, Кр = 10–68,5. При больших отрицательных значениях 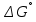 (< – 40 кДж/моль) константа равновесия процесса Кр очень велика, и реакция почти необратима. Большое положительное значение (< – 40 кДж/моль) константа равновесия процесса Кр очень велика, и реакция почти необратима. Большое положительное значение 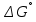 (> + 40 кДж/моль) указывает на то, что без удаления одного из продуктов реакции процесс в обычных условиях не идет (Кр очень мала). Например, при температуре 298 К и (> + 40 кДж/моль) указывает на то, что без удаления одного из продуктов реакции процесс в обычных условиях не идет (Кр очень мала). Например, при температуре 298 К и 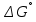 = + 40 кДж/мольlg(Kp) = - 40000/(2,3 . 8,314 . 298) = –7 и Кр = 10–7. В рассмотренном выше примере Кр = 10–68,5, что свидетельствует о том, что осуществить процесс против термодинамической направленности можно только при использовании внешней электрической энергии. = + 40 кДж/мольlg(Kp) = - 40000/(2,3 . 8,314 . 298) = –7 и Кр = 10–7. В рассмотренном выше примере Кр = 10–68,5, что свидетельствует о том, что осуществить процесс против термодинамической направленности можно только при использовании внешней электрической энергии.Если в системе протекает окислительно-восстановительный процесс, то основной характеристикой равновесия в этом процессе является электрохимический потенциал реакции. Потенциал каждого из участников реакции относительно стандартного водородного электрода определяется выражением (В): ε = ε0 + RT/(nF) – ln(aокисл./aвосст.), которое при 25 °С принимает вид ε = ε0 + + 0,059 . п . lп(аокисл./авосст.). Предположим, рассматриваем процесс Авосст.+ Вокисл. = Ввосст.+ Аокисл.. Здесь протекают две реакции: Авосст. - пе = Аокисл. и Вокисл. + пе = Ввосст.. Для всего этого процесса потенциал определяется какЭДС элемента (определяемая как разность потенциалов участников процесса): 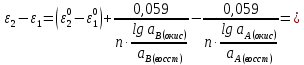 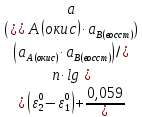 Ho, как отмечено выше, отношение 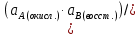 =KP, а разность( =KP, а разность(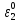 – – 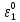 )= E˚ – стандартная величинаЭДС . Поэтому в момент равновесия реакции E˚ = 2,3RT/(n · F) · lg(Кр). Но, как показано ранее, 2,3RT·lg(Kp) = –ΔG˚. Следовательно, Е˚ = –ΔG°/(nF), то есть потенциал процесса можно определить во величине его энергии Гиббса и числу электронов, участвующих в реакции. Поэтому для рассмотренного выше окислительно-восстановительного процесса электролитического разложения сернокислого цинкаЕ°=-[-384000/(2·96500)]=1,99B )= E˚ – стандартная величинаЭДС . Поэтому в момент равновесия реакции E˚ = 2,3RT/(n · F) · lg(Кр). Но, как показано ранее, 2,3RT·lg(Kp) = –ΔG˚. Следовательно, Е˚ = –ΔG°/(nF), то есть потенциал процесса можно определить во величине его энергии Гиббса и числу электронов, участвующих в реакции. Поэтому для рассмотренного выше окислительно-восстановительного процесса электролитического разложения сернокислого цинкаЕ°=-[-384000/(2·96500)]=1,99B Для графического изображения равновесия электрохимических процессов, протекающих в водной среде, удобны диаграммы зависимости ε =f(pH), называемые диаграммами Пурбе, получившие широкое применение главным образом благодаря работам Пурбе и его школы. При построении этих диаграмм поле диаграммы прежде всего разбивают на три области, нанося на него линии восстановления водорода и окисления кислорода при электролитическом разложении воды, а уже затем рассчитывают области существования различных фаз рассматриваемого процесса. Устойчивость тех или иных фаз будет определяться их месторасположением в поле диаграммы: фазы, находящиеся ниже линии восстановления водорода, способствуют разложению воды с выделением газообразного Н2, а фазы, находящиеся выше линии окисления кислорода, способствуют разложению воды с выделением газообразного О2. Диаграммы Пурбе дают обоснование некоторых возможных методов защиты металлов от коррозии. Из диаграммы также следует, что при повышении рН до известных пределов начинается образование новых твердых неметаллических фаз, которые, возникая на поверхности металла, могут защищать его от коррозии и переводить в состояние пассивности. При использовании диаграмм Пурбе необходимо иметь в виду, что основанные на них выводы являются лишь термодинамически наиболее вероятными; они указывают на термодинамическую возможность или невозможность того или иного процесса. В реальных условиях не исключены отклонения от сделанных выводов и протекающие процессы могут быть из-за кинетических ограничений иными, чем те, которые следуют из общих термодинамических соотношений. Методика построения диаграмм Пурбе В данной курсовой работе рассматривается методика построения диаграммы Пурбе на примере свинец металлический – вода. При построении диаграммы необходимо рассмотреть условия термодинамического равновесия между ионами в растворе, ионами и твердыми фазами и между самими твердыми фазами в присутствии воды. И для этого необходимо знать энергию Гиббса всех участников системы. Таблица 1 Энергия Гиббса компонентов системы Pb - H2O
Равновесие между катионом Pb2+ и Pbмет по химической реакции: 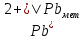 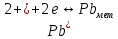 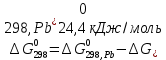 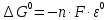 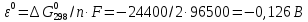 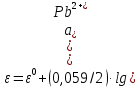 Потенциал данного перехода является линейной функцией активности катионов Pb2+, то есть каждому значению активности ионов свинца в растворе, находящихся в равновесии с металлом, соответствует свое значение потенциала окислительного процесса. При этом потенциал данной реакции не зависит от pH среды. Если 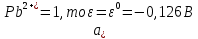 Если 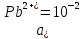 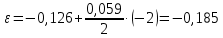 В ВРавновесие между катионом Pb2+ и гидроксидом Pb(OH)2 по химической реакции: 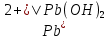 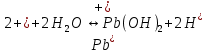 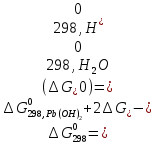 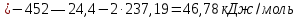 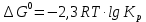 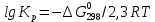 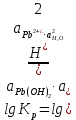 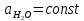 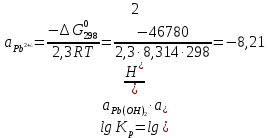 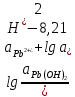 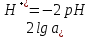 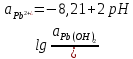 Если 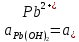 -8,21+2pH=0 pH=4,1 При рН< 4,1 в растворе в основном присутствуют катионы Pb2+, а при рН> 4,1 гидроксид Pb(OH)2 Равновесие между катионом Pb2+ и гидроксидами [Pb(OH)]+ по химической реакции: 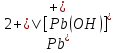 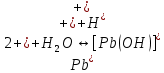 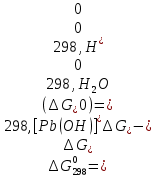 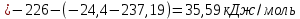 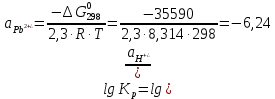 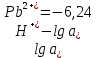 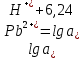 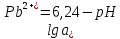 Если 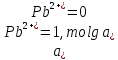 Тогда, 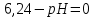 pH=6,24 С повышением активности ионов свинца в растворе рН гидрообразования сдвигается в более кислую область и наоборот. Равновесие между гидроксидами 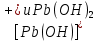 по химической реакции: по химической реакции: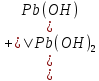 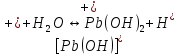 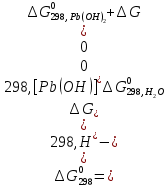 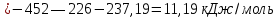 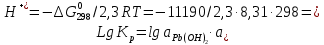 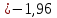 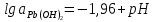 Пусть 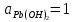 , то , то  pH=1,96 При этом расчете у нас получается, что фаза Pb(OH)2 смещается в область ионов Pb2+, а это не возможно, то есть этой фазы не будет. Равновесие между твердой фазой 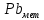 и гидроксидом и гидроксидом 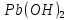 по химической реакции: по химической реакции: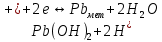 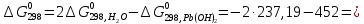 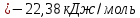 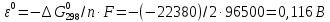 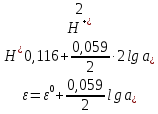 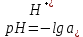 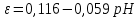 При pH=0 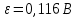 При pH=14 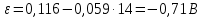 Равновесие между твердой фазой 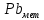 и гидроксидом и гидроксидом 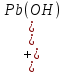 по химической реакции: по химической реакции: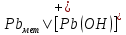 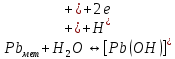 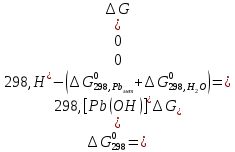 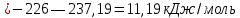 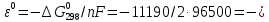 0,058 B 0,058 B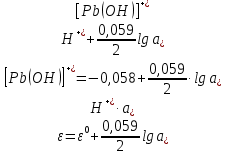 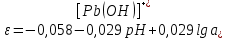 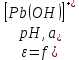 Угловой коэффициент: 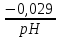 Если 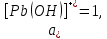 то то 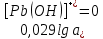 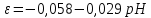 pH=0 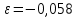 B BpH=14 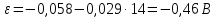 Таблица 2 Составляем таблицу с учетом возрастания pH
Диаграмма Пурбе для системы свинец-вода  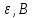                     1,2  1      0,8     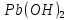 0,6  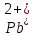     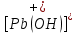 0,4  0,2       0      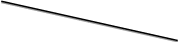 -0,2  -0,4       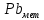 -0,6  -0,8      -1  -1,2   рН рН0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Заключение На сводной диаграмме системы границы полей устойчивости конкретных фаз определяются точками пересечения равных изолиний (то есть линий, отвечающих одинаковым значениям активностей ионов). Так, при активности всех присутствующих ионов, равных единице (аi = 1), в левой части диаграммы при 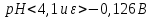 , находится область устойчивого состояния катионов свинца Pb2+ в растворе. В правой части диаграммы при , находится область устойчивого состояния катионов свинца Pb2+ в растворе. В правой части диаграммы при 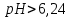 и и 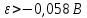 , при , при 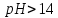 и и 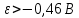 , находится область стабильности гидроксид , находится область стабильности гидроксид 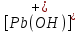 . Между этими областями расположены область стабильного существования гидроксида cвинца . Между этими областями расположены область стабильного существования гидроксида cвинца 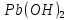 . Металлический свинец нестабилен в контакте с водными растворами, поэтому он будет переходить в зависимости от рН среды в ионы . Металлический свинец нестабилен в контакте с водными растворами, поэтому он будет переходить в зависимости от рН среды в ионы 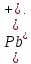 Из приведенной диаграммы видно, что линии, параллельные оси абсцисс (горизонтальные), соответствуют равновесию реакций, в которых не участвуют ионы Н+ и ОН-. Линии, параллельные оси ординат (вертикальные), изображают равновесие реакций, в которых не происходит передача электронов. В тех же случаях, когда протекают окислительно-восстановительные процессы с участием ионов Н+ и ОН-, линии на диаграмме имеют определенные углы наклона. В совокупности эти линии определяют границы существования конкретных фаз. Список использованных источников 1. Жучков И.А. Основы теории электрометаллургических процессов: учеб. пособие / И.А. Жучков. – Иркутск: Изд-во ИрГТУ, 2000. – 107 стр. 2. Антропов Л.И. Теоретическая электрохимия: Учеб. для хим.-технолог. спец. вузов. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1984. – 519 с. |
