Курсовая работа по дисциплине Теория принятия решений
 Скачать 138.27 Kb. Скачать 138.27 Kb.
|
|
Федеральное агентство по образованию ГОУ ВПО УГТУ-УПИ Кафедра автоматизированных систем управления Курсовая работа по дисциплине «Теория принятия решений» Студент гр. Р - 35021 Пушняков С.А. (09521531) ______________________ (подпись) Преподаватель Черногородова Г.М. ______________________ (подпись, дата) Оценка работы ______________________ Екатеринбург 2008 ОглавлениеОглавление 3 Задача 1 4 Содержательная постановка 4 Математическая модель 6 Задача 2 7 Содержательная постановка 7 Математическая модель 8 Задача 3 10 Содержательная постановка 10 Математическая модель 12 Задача 4 13 Содержательная постановка 13 Математическая модель 14 Задача 5 15 Содержательная постановка 15 Математическая модель 16 Задача 6 17 Содержательная постановка 17 Математическая модель 18 Задача 7 19 Содержательная постановка 19 Математическая модель 20 Список литературы 21 Задача 1Содержательная постановкаДля изготовления трех видов велосипедов: детского, спортивного и универсального используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице 1. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного велосипеда каждого вида.
таблица 1 Требуется определить, сколько велосипедов и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Математическая модельПредположим, что будет изготовлено x1 единиц детских велосипедов, 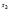 единиц – спортивных и единиц – спортивных и 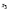 единиц – универсальных. единиц – универсальных. 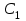 - прибыль с продаж детских велосипедов, - прибыль с продаж детских велосипедов, 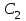 - спортивных, - спортивных, 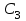 - универсальных. - универсальных. 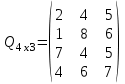 матрица затрат на производство деталей для велосипедов. 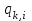 - удельные затраты на производство определённой детали на определённом оборудовании. - удельные затраты на производство определённой детали на определённом оборудовании. 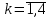 - тип оборудования, - тип оборудования, 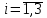 вид велосипеда. вид велосипеда.Математическая модель в общем виде: 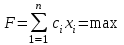 и и 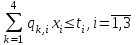 где 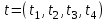 - фонд рабочего времени где - фонд рабочего времени гдеМатематическая модель для нашей задачи: 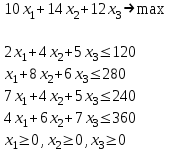 Задача 2Содержательная постановкаПродукцией городского молочного завода являются молоко, кефир и сметана, расфасованные в бутылки. На производство 1 т молока, кефира и сметаны требуется соответственно 1010, 1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 машино-часов. На расфасовке 1 т сметаны заняты специальные автоматы в течение 3,25 часов. Всего для производства цельномолочной продукции завод может использовать 136000 кг молока. Основное оборудование может быть занято в течение 21,4 машино-часов, а автоматы по расфасовке сметаны – в течение 16,25 часов. Прибыль от реализации 1 т молока, кефира и сметаны соответственно равна 30, 22 и 136 руб. Завод должен ежедневно производить не менее 100 т молока, расфасованного в бутылки. Эти же данные представлены в таблицах 1 и 2. На производство другой продукции не имеется никаких ограничений.
таблица 1
таблица 2 Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной. Математическая модельПредположим, что будет изготовлено x1 тонн молока, 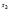 тонн кефира и тонн кефира и 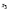 тонн сметаны. тонн сметаны. 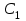 - прибыль с продаж молока, - прибыль с продаж молока, 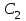 - кефира, - кефира, 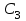 - сметаны. - сметаны. 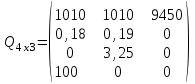 матрица затрат на производство. 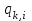 - удельные затраты на производство определённых изделий. - удельные затраты на производство определённых изделий. 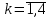 , , 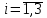 - вид молочного продукта. - вид молочного продукта.Математическая модель в общем виде: 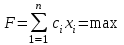 и и 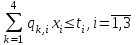 где 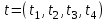 - фонд рабочего времени и затрат исходного ресурса - фонд рабочего времени и затрат исходного ресурсаМатематическая модель для нашей задачи: 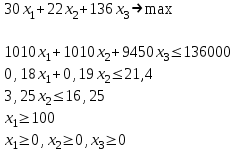 Задача 3Содержательная постановкаФирма - булочно-кондитерский комбинат выпускает следующие виды продукции указанные в таблице 1:
таблица 1 Для выпуска этих видов продукции необходимы ресурсы, которые перечислены в таблице 2, здесь же указано количество каждого вида ресурса, имеющегося на складе.
таблица 2 Далее в таблице 3 приведена рецептура, т.е. необходимое количество каждого вида ресурса для приготовления каждого вида продукции.
таблица 3 Так же в таблице 4 приведена отпускная цена на единицу каждого вида продукции.
таблица 4 Фирме необходимо определить такой оптимальный план выпуска каждого вида продукции: чего и в каком количестве приготовить, чтобы при имеющихся в БКК ресурсах получить максимальный доход от реализации Математическая модельПредположим, что будет изготовлено 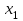 - булок, - булок, 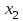 - пирожных, - пирожных, 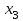 - ватрушек, - ватрушек, 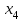 - коржиков, - коржиков, 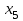 - слоёнок. - слоёнок. 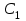 - прибыль булок, - прибыль булок, 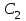 - пирожных, - пирожных, 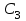 - ватрушек, - ватрушек, 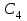 - коржиков, - коржиков, 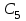 - слоёнок, . - слоёнок, . 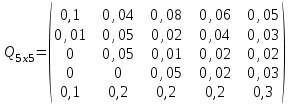 матрица затрат на производство. 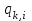 - удельные затраты на производство определённых изделий. - удельные затраты на производство определённых изделий. 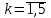 - вид затрачиваемого ресурса, - вид затрачиваемого ресурса, 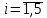 - вид конечного продукта. - вид конечного продукта.Математическая модель в общем виде: 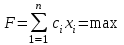 и и 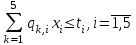 где 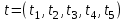 - количество исходного ресурса на складе. - количество исходного ресурса на складе.Математическая модель для нашей задачи: 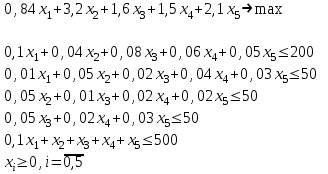 Задача 4Содержательная постановкаНа предприятии образовалось 150 м3 свободных остатков пиломатериалов и 1600 м2 листового стекла. Эти материальные ресурсы можно использовать в цехе товаров народного потребления, к примеру, для производства сервантов, книжных полок и зеркал (маркетологи «дают добро» на возможность сбыта этих товаров по следующим ценам: сервант – 91, книжная полка – 14.5, зеркало – 11 денежных единиц), данные на затраты каждого ресурса приведены в таблице 1.
таблица 1 Математическая модельПредположим, что 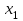 - кол-во сервантов, - кол-во сервантов, 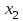 - книжных полок, - книжных полок, 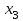 - зеркал. - зеркал. 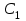 - прибыль с продажи серванта , - прибыль с продажи серванта , 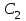 - книжной полки, - книжной полки, 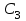 - зеркало. - зеркало.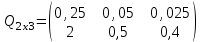 матрица затрат на производство. матрица затрат на производство. 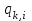 - удельные затраты на производство определённых изделий. - удельные затраты на производство определённых изделий. 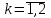 - вид затрачиваемого ресурса, - вид затрачиваемого ресурса, 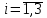 - вид конечного продукта. - вид конечного продукта.Математическая модель в общем виде: 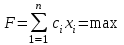 и и 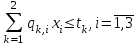 где 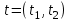 - количество исходного ресурса. - количество исходного ресурса.Математическая модель для нашей задачи: 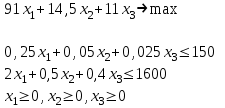 Задача 5Содержательная постановкаМагазин оптовой торговли реализует три вида продукции: Молоко, мясо, хлеб. Для этого используются два ограниченных ресурса - полезная площадь помещений, которая с учётом оборачиваемости составляет 450 кв метров, и рабочее время работников магазина – 600 человеко-часов. Товарооборот должен быть не меньше 240 тыс. рублей. Необходимо разработать план товарооборота, доставляющий максимум прибыли. Затраты ресурсов на реализацию и получаемая при этом прибыль представлены в таблице 1.
таблица 1 Математическая модельПредположим, что 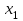 - молоко, - молоко, 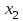 - мясо, - мясо, 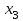 - хлеб. - хлеб. 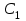 - прибыль с молока, - прибыль с молока, 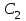 - мяса, - мяса, 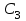 - хлеба. - хлеба.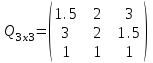 матрица затрат на производство. матрица затрат на производство. 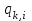 - удельные затраты на производство определённых изделий. - удельные затраты на производство определённых изделий. 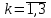 - вид затрачиваемого ресурса, - вид затрачиваемого ресурса, 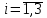 - вид конечного продукта. - вид конечного продукта.Математическая модель в общем виде: 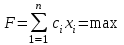 и и 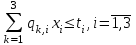 где 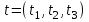 - количество исходного ресурса. - количество исходного ресурса.Математическая модель для нашей задачи: 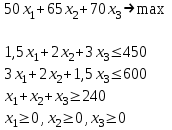 Задача 6Содержательная постановкаДиета включает продукты 4 основных групп: сладости, домашняя еда, напитки, и фаст-фуд. В настоящее время доступны следующие представители этих групп : пирожные, 50с за шт., котлеты, 20с за шт., кола, 30с за бут., биг-мак, 80с за шт. В единице продукта содержится следующее количество некоторых веществ, эти данные представлены в таблице 1:
таблица 1 Есть ограничения на вещества в день: Сумма калорий ≥ 500, сумма витаминов ≥ 6, сумма сахара ≥ 10, сумма жира ≥ 8. Надо получить набор, при котором человек будет получать необходимое число веществ, но стоимость этого набора должна быть минимальна. Математическая модельПредположим, что будет куплено 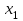 - пирожных, - пирожных, 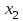 - котлет, - котлет, 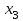 - бутылок колы, - бутылок колы, 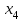 - биг-маков, - биг-маков, 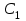 - стоимость пирожных, - стоимость пирожных, 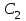 - котлет, - котлет, 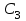 - бутылки колы, - бутылки колы, 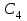 - биг-мака. - биг-мака. 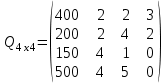 матрица показывающая содержание веществ. 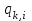 - количество определённого вещества. - количество определённого вещества. 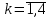 - вид продукта, - вид продукта, 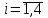 - вид вещества. - вид вещества.Математическая модель в общем виде: 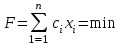 и и 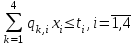 где 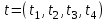 - минимальное количество вещества в день. - минимальное количество вещества в день.Математическая модель для нашей задачи: 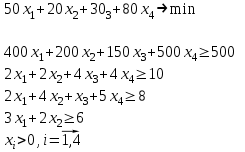 Задача 7Содержательная постановкаЛесничество имеет 24 га свободной земли под паром и заинтересовано извлечь из нее доход. Оно может выращивать саженцы быстрорастущего гибрида новогодней ели, которые достигают спелости за один год, или бычков, отведя часть земли под пастбище. Деревья выращиваются и продаются в партиях по 1000 штук. Требуется 1.5 га для выращивания одной партии деревьев и 4 га для вскармливания одного бычка. Лесничество может потратить только 200 ч. в год на свое побочное производство. Практика показывает, что требуется 20 ч. для культивации, подрезания, вырубки и пакетирования одной партии деревьев. Для ухода за одним бычком также требуется 20 ч. Лесничество имеет возможность израсходовать на эти цели 6 тыс. руб. Годовые издержки на одну партию деревьев выливаются в 150 руб. и 1,2 тыс. руб. на одного бычка. Уже заключен контракт на поставку 2 бычков. По сложившимся ценам, одна новогодняя ель принесет прибыль в 2,5 руб., один бычок - 5 тыс. руб. Математическая модельПредположим, что x1 - количество откармливаемых бычков в год;x2 - количество выращиваемых партий быстрорастущих новогодних елей по 1000 шт. каждая в год. 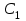 - прибыль с продажи ели, - прибыль с продажи ели, 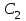 - бычка. - бычка.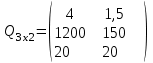 матрица затрат. 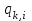 - удельные затраты на производство. - удельные затраты на производство. 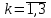 - вид затрачиваемого ресурса, - вид затрачиваемого ресурса, 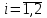 . .Математическая модель в общем виде: 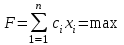 и и 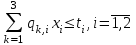 где 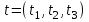 - количество исходного ресурса. - количество исходного ресурса.Математическая модель для нашей задачи: 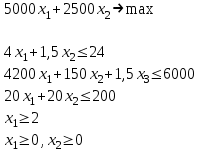 Список литературыКофман, А. Методы и модели исследования операций М. : Мир Т. 3 : Целочисленное программирование 1977. Костевич Л.С. Математическое программирование: Информ. технологии оптимальных решений. – Мн., Новое знание, 2003 Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Дрофа, 2004 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Продукция
Продукция