|
КБ (ответы). 1. Содержательная постановка задачи создание эвм, функционирующей в условиях разрушения программноаппаратной среды
1. Содержательная постановка задачи создание ЭВМ, функционирующей в условиях разрушения программно-аппаратной среды
Моделирование вообще, а математическое моделирование в частности, определяют технологию познания. Насколько адекватно мы моделируем действительность, настолько успешно мы её познаем. На основе адекватного познания мы и адекватно существуем в действительности. Мерой адекватности является полнота учёта закономерностей рассматриваемой предметной области. Базовым законом является закон сохранения целостности объекта, сформулированный автором данной статьи. Сущность этого закона определяется неразрывной связью объекта и его движения и характеризуется как взаимная трансформация свойств объекта и свойств его движения при заданном, чётко фиксированном предназначении[1]. Практически предназначение количественно должно определяться значением показателя эффективности функционирования объекта. Не учитывая на практике закон сохранения целостности объекта, мы сталкиваемся с тем, что результат применения созданной нами объекта не соответствует ожидаемому.
Как раз при разработке компьютерных технологий этот закон в полной для практики мере не учитывается, что не позволяет адекватно реагировать как на сбои аппаратной части, так несанкционированные программные воздействия извне. Большинство современных ЭВМ следуют «модели фон Неймана». Самой важной отличительной чертой этой модели остаётся принцип единой «линейной памяти», которая адресуется последовательными номерами ячеек и в которой команды неотличимы от данных.
Как и все объекты окружающей действительности, программная система (ПС) существует в пространстве и времени и характеризуется пространственно - временными состояниями (ПВС). Множество возможных ПВС ПС есть декартово произведение множества всех состояний пронумерованных ячеек памяти (Х) и множества натуральных чисел (например N), которыми пронумерованы ячейки, и которое в процессе функционирования ПС тождественно временной оси - множеству Т.
ПС реализуется логической последовательностью выполнения команд в памяти при функционировании ПС. Если множество Х есть множество возможных состояний памяти ЭВМ, то X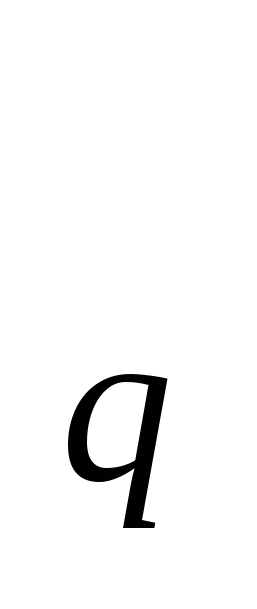 - множество требуемых состояний памяти в процессе реализации ПС, а Т - множество требуемых состояний памяти в процессе реализации ПС, а Т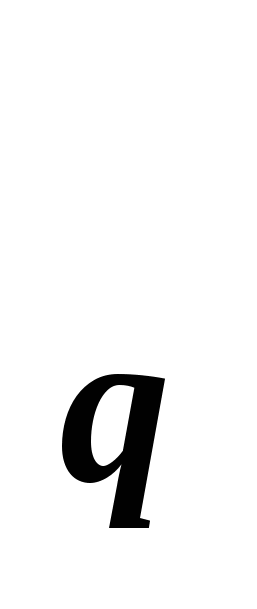 - множество требуемых временных состояний памяти в процессе реализации ПС. Множество Q=X - множество требуемых временных состояний памяти в процессе реализации ПС. Множество Q=X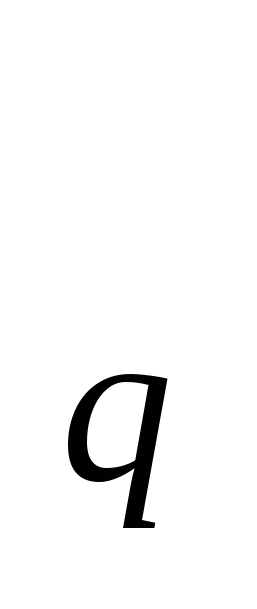 ×Т ×Т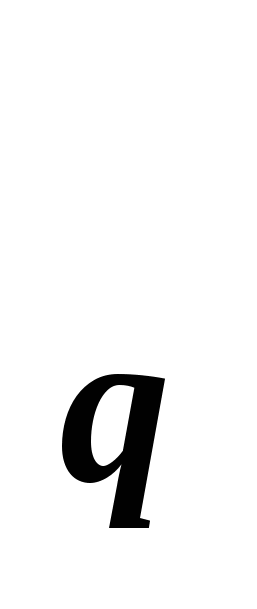 есть множество требуемых ПВС ПС при её реализации в памяти. То есть, это математическая модель, описывающая логическую последовательностью выполнения команд в памяти при функционировании ПС. Физически при реализации ПС нам надо выбрать определённую логическую последовательность команд, размещённых в памяти. Математически это можно осуществить только на основе алгебраической операции, связанной со свойствами несущего множества. (Новое направление в абстрактной алгебре[2]). Применяя такую алгебраическую операцию на множестве возможных состояний памяти ЭВМ, мы можем моделировать процесс функционирования ПС в зависимости от множества возможных ПВС памяти. Множество ПВС памяти может изменяться как из-за выхода из строя (разрушения) аппаратной части, так и из-за целенаправленного изменения извне, как содержания команд, так и последовательности их выполнения. есть множество требуемых ПВС ПС при её реализации в памяти. То есть, это математическая модель, описывающая логическую последовательностью выполнения команд в памяти при функционировании ПС. Физически при реализации ПС нам надо выбрать определённую логическую последовательность команд, размещённых в памяти. Математически это можно осуществить только на основе алгебраической операции, связанной со свойствами несущего множества. (Новое направление в абстрактной алгебре[2]). Применяя такую алгебраическую операцию на множестве возможных состояний памяти ЭВМ, мы можем моделировать процесс функционирования ПС в зависимости от множества возможных ПВС памяти. Множество ПВС памяти может изменяться как из-за выхода из строя (разрушения) аппаратной части, так и из-за целенаправленного изменения извне, как содержания команд, так и последовательности их выполнения.
Под разрушением программно-аппаратной среды будем понимать выход (или вывод) из строя аппаратной части и целенаправленной изменение извне, как требуемого содержания команд, так и требуемой последовательности их выполнения.
Для учёта разрушения программно-аппаратной среды получим новый класс алгебраических операций, связанных со свойствами несущего множества, и рассмотрим алгоритм её применения.
|
2. Системообразующие основы моделирования. Модель действия.
Рассмотрим общий подход к одновременному синтезу модели системы и способов её применения. Будем характеризовать систему на каждый момент времени tT n-ым вектором состояний x со следующими компонентами:
- компоненты, отражающие расположение в пространстве;
- компоненты, отражающие состояние агрегатов и подсистем, зоны воздействия, влияния, обмена и т.п..
В процессе функционирования в момент времени tT вектор x принимает значение элемента из множества допустимых значений X. T - допустимая длительность функционирования системы. Тогда процесс функционирования системы будем характеризовать парой элементов из множеств T и X, которую определим следующим образом.
Определение 2.1. Множество R = X×T (декартово произведение множеств X и T) есть множество допустимых значений ПВС системы, зон воздействия, обмена и т.п. в процессе решения целевой задачи.
На множестве R в процессе синтеза модели системы формируется множество требуемых ПВС системы, которое определим следующим образом.
Определение 2.2. Множество требуемых пространственно - временных состояний (ПВС) системы (объекта), зон воздействия, обмена и т.п. при решении целевой задачи QR называется районом сосредоточения основных усилий системы (РСОУ). (В данной статье это модель функционирования ПС. Программа в действии).
Q –данное множество есть модель действия в силу следующего. Объект существует в пространстве и времени. Движение есть изменение пространства и времени. Поэтому декартово произведение множеств требуемых пространственных и временных состояний определяет движение. Каково действие (проявление энергии), таково и движение.
Так как обычно процесс применения характеризуется, в первую очередь способом, то определим его и сравним с РСОУ.
Определение 2.3. Способ действий - это порядок и приемы использования системы для решения целевых задач. (Способ преобразований символов в памяти).
Базовые элементы способа действий.
- последовательность реализации возможностей системы, согласованной и объединенной целью функционирования (предназначением);
- район сосредоточения основных усилий системы;
- характер изменения ПВС системы.
Сопоставляя поэлементно определения РСОУ и Способа действий можно увидеть в этих понятиях общую сущность, при этом характеристики РСОУ носят конструктивный характер и всегда вычислимы.
На каждом элементе множества Q система выполняет "работу" с определенной производительностью, определение которой следующее.
Определение 2.4. Производительностью системы называется величина (функция), характеризующая способность решения определенного количества целевых задач системой в единицу времени. (Например, количество требуемых символов, преобразованных в памяти за единицу времени).
Производительность системы в области компьютерных технологий это базовая характеристика процессора ЭВМ. Производительность системы зависит от возможностей системы и механизмов реализации этих возможностей. Поэтому приведем соответствующие определения.
Определение 2.5. Возможности - это количественные и качественные показатели, характеризующие способность системы по выполнению определенных целевых задач за установленное время в конкретной обстановке. Количественно оцениваются вектором возможностей v(r)V, где V ограниченное, замкнутое множество. (V- множество команд ЭВМ, ресурсы; в том числе и временные).
Особо необходимо рассмотреть вопрос определения компонент вектора возможностей, так как команды определяются как функции в виде правил, а не в виде графиков (как, например, в математическом анализе). Для этого необходимо использовать аппарат лямбда-исчисления [4].
Определение 2.6. Эффективность применения (ЭП) это свойство системы, которое характеризуется степенью реализации возможностей системы в процессе решения целевых задач. Оценивается величиной I (показатель ЭП) с учётом затрат материальных средств, различных ресурсов и времени. (Второе базовое понятие). (В статье показатель ЭП - требуемое количество требуемых символов, реализующее логическую последовательностью выполнения команд в памяти при функционировании целевой ПС).
Для существующих ЭВМ разработчик ПС «пишет» её в виде цепочки символов, реализующей логическую последовательностью выполнения команд в памяти при функционировании целевой ПС. Для такого класса систем эффективность применения (свойство ПС) характеризуется 2-мя состояниями: «решает» или «не решает» ПС поставленную задачу. Или если показатель ЭП I равен требуемому количеству требующихся символов, то задача решается, если I не равен, то задача не решается. При этом значение I обеспечивает требуемое количество, а как будет показано в следующем определении 2.7., множество правил исполнения команд ЭВМ(U) обеспечивает номенклатуру требующихся символов. На практике получается, что разработчик алгоритмически реализует целостность ПС и доверяет её (целостность ПС) памяти ЭВМ, которая способна реализовать ПС только в идеальных, расчётных условиях – как без выхода из строя аппаратной части, так и без целенаправленного изменения, как содержания, так и последовательности выполнения команд злоумышленником.
Естественно в такой постановке не рассматривать алгоритмические ошибки и некорректности на этапе разработки ПС.
Для достижения требуемого уровня ЭП должны существовать определённые механизмы реализации возможностей, заложенных в системе разработчиком. У ЭВМ эти механизмы характеризуются правилами выполнения команд, то есть отношениями команд и механизмами их исполнения. Правила выполнения команд в модели реализуются управлением.
Определение 2.7. Управление системой - это целенаправленное воздействие разработчика, руководителя системы на систему с целью обеспечения требуемой ЭП в различных условиях обстановки. Реализуется вектором управления u(r)U, где U - замкнутое, ограниченное множество. (U - множество правил выполнения команд ЭВМ).
Как и в случае рассмотрения вектора возможностей необходимо рассмотреть вопрос определения компонент вектора управления, так как компоненты вектора управления определяются как функции в виде правил, а не в виде графиков (как, например, в математическом анализе). Для этого также необходимо использовать аппарат лямбда-исчисления [4].
Процессор ЭВМ на множестве требуемых пространственно-временных состояний памяти осуществляет требуемые преобразования требуемых символов. Поэтому естественно предположить, что система в каждой точке пространственной области Q "что-то делает" с определенной производительностью в соответствии со своим предназначением, характеризуемой функцией (r). (То есть плотность распределения производительности системы в пространстве). Если с каждой точкой М определенной пространственной области связана некоторая скалярная или векторная величина, то говорят, что задано поле этой величины, соответственно, скалярное или векторное. Предположим, что система в процессе функционирования формирует некоторое поле эффективности I (Q), (интеграл – функция множества, по которому осуществляется интегрирование), где Q R. Зная свойства поля и проинтегрировав его ППЭ (r) по области Q можно получить результат действия системы по всей области Q(РСОУ). Поэтому применим понятие потенциала поля для определения свойств системы.
Определение 2.8. Функцию (r)=(u(r),v(r),r), где u(r), v(r), соответственно, вектора управления и возможностей, а r Q, будем называть потенциалом поля эффективности (ППЭ) разрабатываемой системы (третье базовое понятие).
Конкретизацией ППЭ является процессор ЭВМ. ППЭ – это модель процессора. Базовой, определяющей характеристикой процессора является показатель производительности. То есть определённое количество преобразованных в памяти символов за определённое количество времени.
Из закона сохранения целостности следует, что кроме соответствующего набора символов, у каждой команды должен быть строго один итог работы процессора по преобразованию символов в памяти. А итог работы – показатель эффективности применения ЭВМ. Это необходимо для того, чтобы система команд удовлетворяла базовым свойствам формальной системы – это полнота, непротиворечивость, разрешимость и независимость аксиом.
Каждая команда это определённый набор символов – слово. Правило выполнения команды - это аксиома. Правилами вывода являются – правило подстановки и правило следования. Теоремами являются блоки программ и сами программы.
ППЭ в соответствии с требуемой пронумерованной последовательностью действий процессора по преобразованию памяти (множество Q) осуществляет преобразование состояний памяти ЭВМ в соответствии с написанной программой. Поэтому будем считать эту функцию моделью системы. В данном случае моделью ЭВМ является (u(r),v(r),r), так как эта модель позволяет определить базовую, интегральную характеристику ЭВМ – это её производительность в зависимости от состояний программно-аппаратной среды. Она обладает свойством
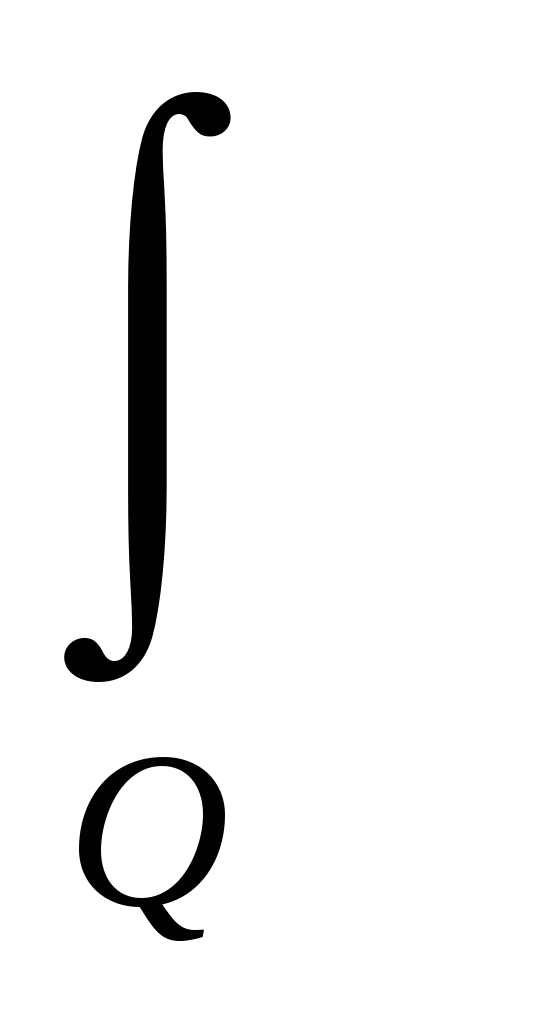 (r)dr = (r)dr = 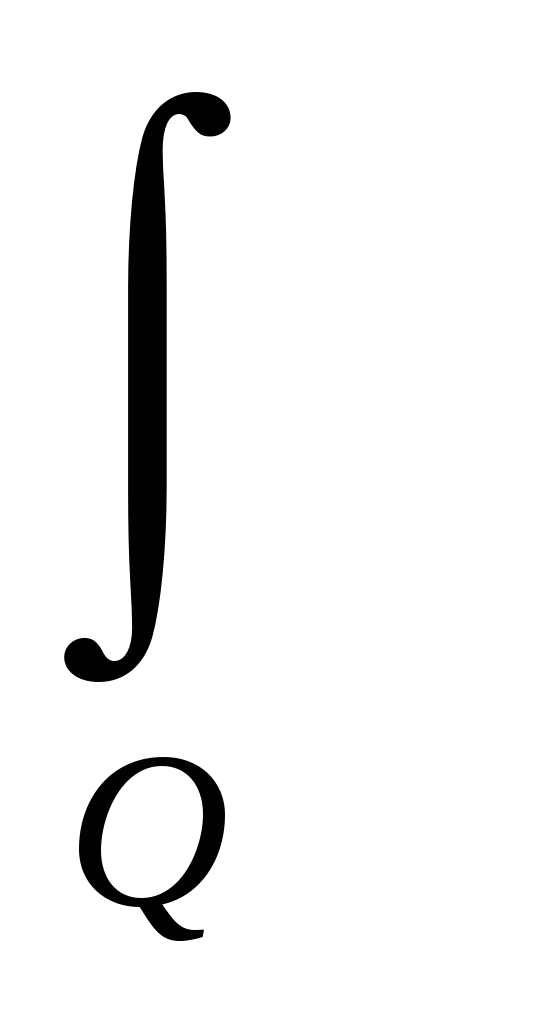 (u(r),v(r),r)dr = I(Q), (2.1.), где I(Q) –показатель ЭП системы, функция множества Q. (u(r),v(r),r)dr = I(Q), (2.1.), где I(Q) –показатель ЭП системы, функция множества Q.
В силу дискретности процессов протекающих в памяти ЭВМ 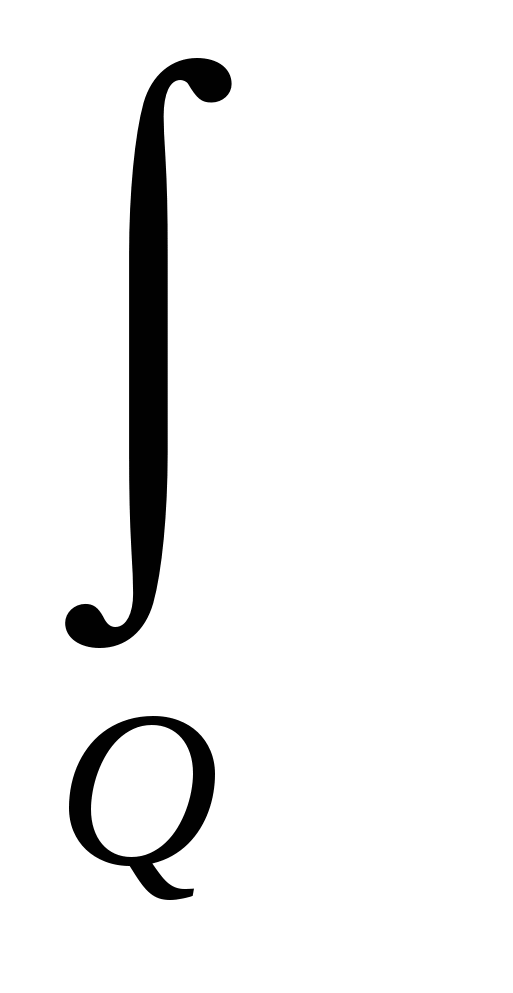 (u(r),v(r),r)dr = (u(r),v(r),r)dr =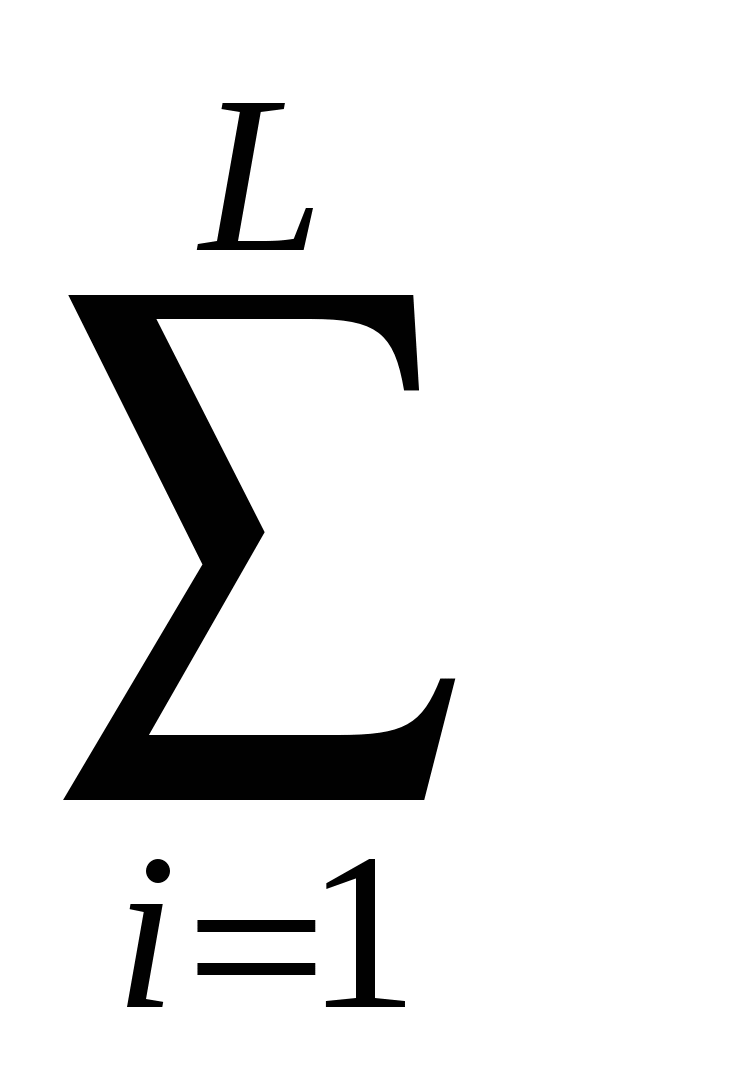 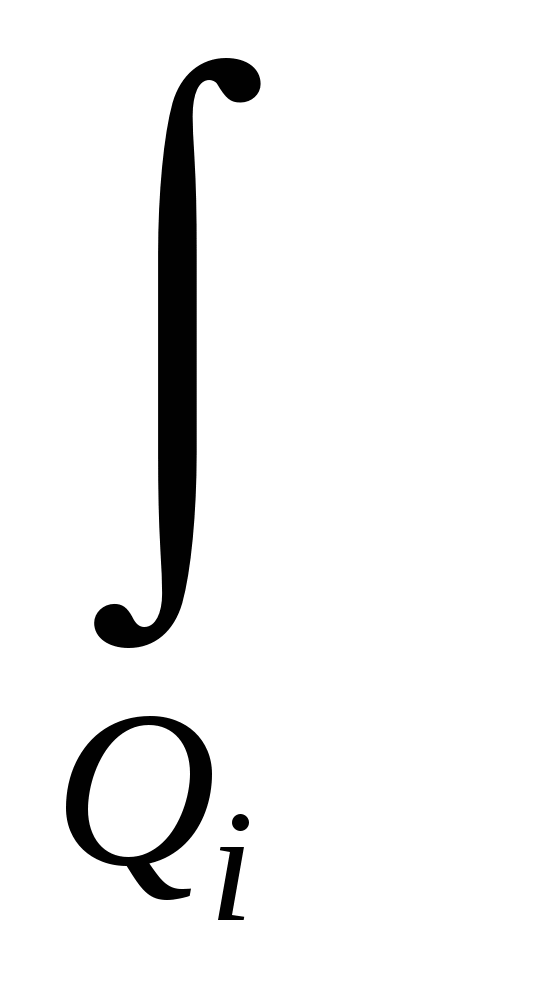 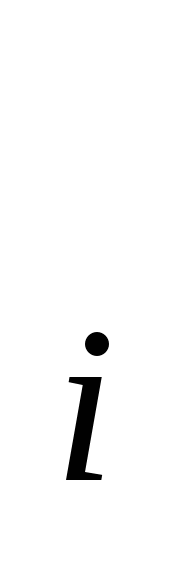 (…)dr, так как Q= (…)dr, так как Q= 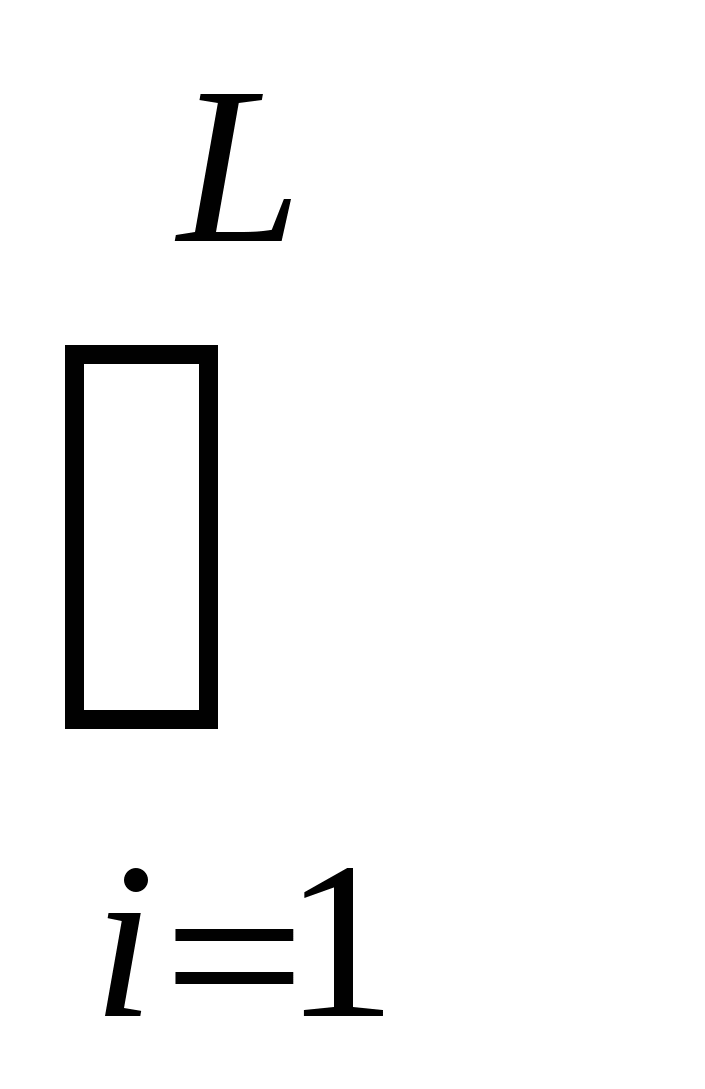 Q Q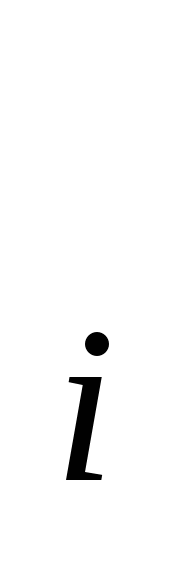 , Q , Q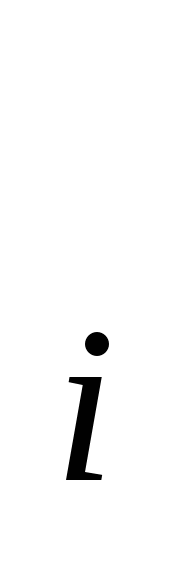  Q Q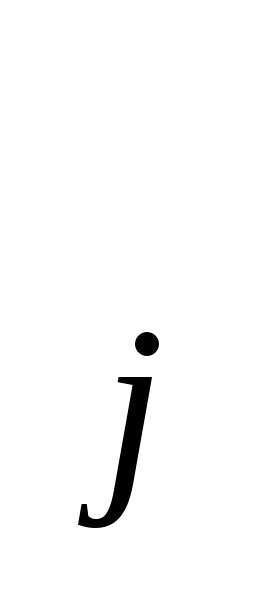 = 0, где L длина упорядоченной, логической последовательности команд рассматриваемой ПС. Q = 0, где L длина упорядоченной, логической последовательности команд рассматриваемой ПС. Q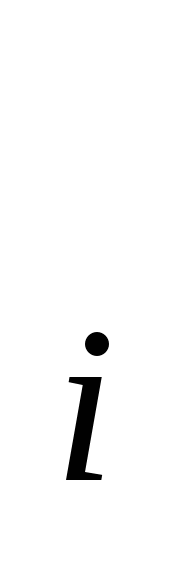 -требуемая, занумерованная и размещённая в памяти ЭВМ, последовательность символов, реализующая i - ую команду, требуемой логической последовательности Q. Тогда из соотношений -требуемая, занумерованная и размещённая в памяти ЭВМ, последовательность символов, реализующая i - ую команду, требуемой логической последовательности Q. Тогда из соотношений 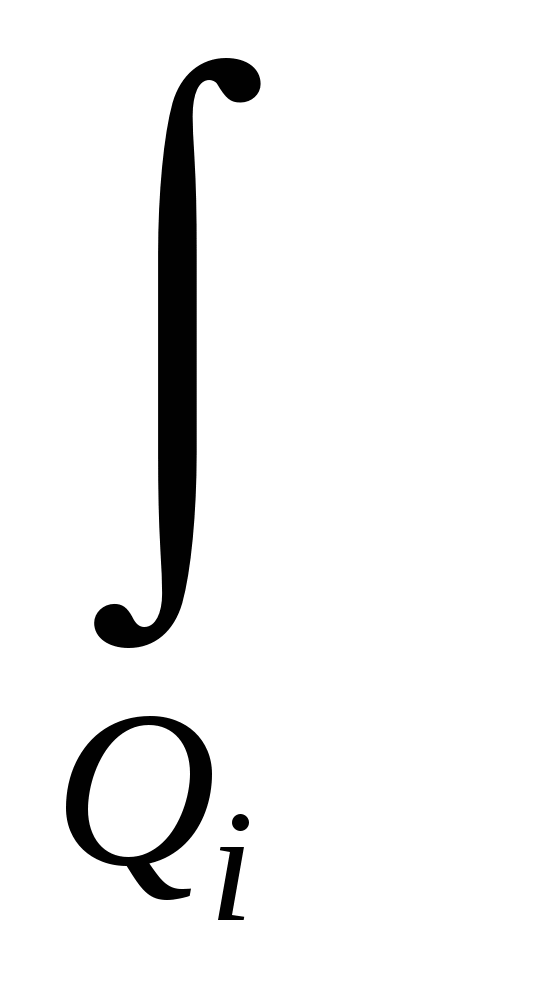 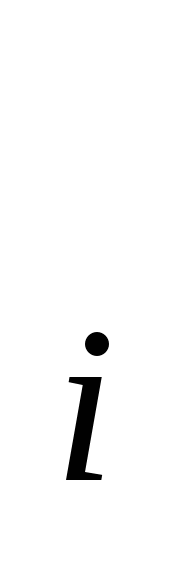 (…)dr = I(Q (…)dr = I(Q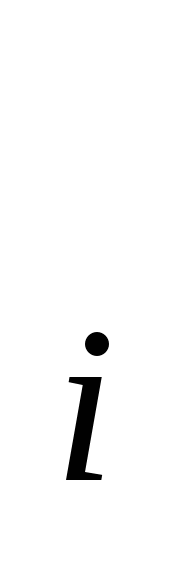 ), ), 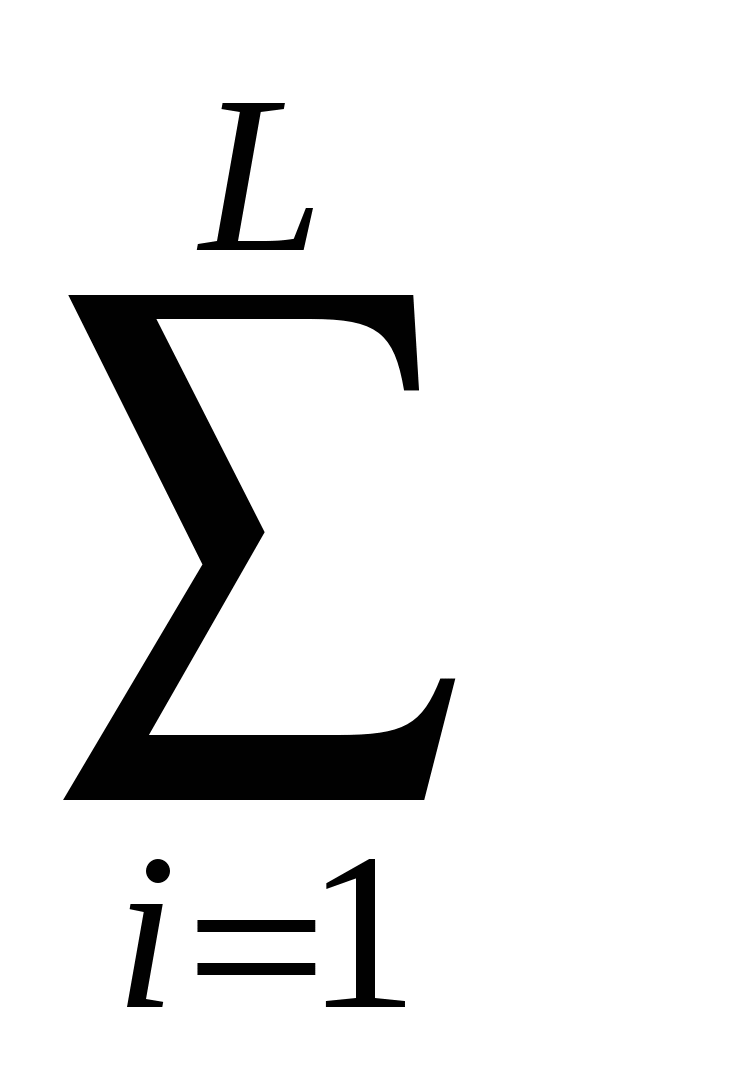 I (Q I (Q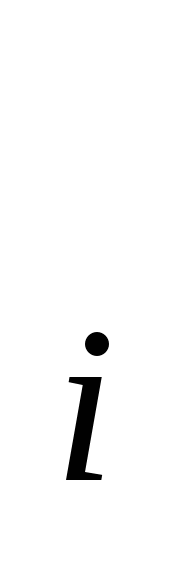 ) = I(Q) следует, что для реализации i-ой команды, указанной в ПС, необходимо осуществить преобразование в памяти I(Q ) = I(Q) следует, что для реализации i-ой команды, указанной в ПС, необходимо осуществить преобразование в памяти I(Q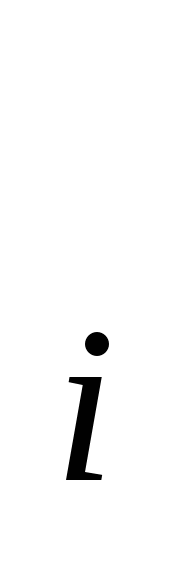 )-го количества символов. Из этого следует, что все свойства i-ой команды должны удовлетворять следующему соотношению )-го количества символов. Из этого следует, что все свойства i-ой команды должны удовлетворять следующему соотношению 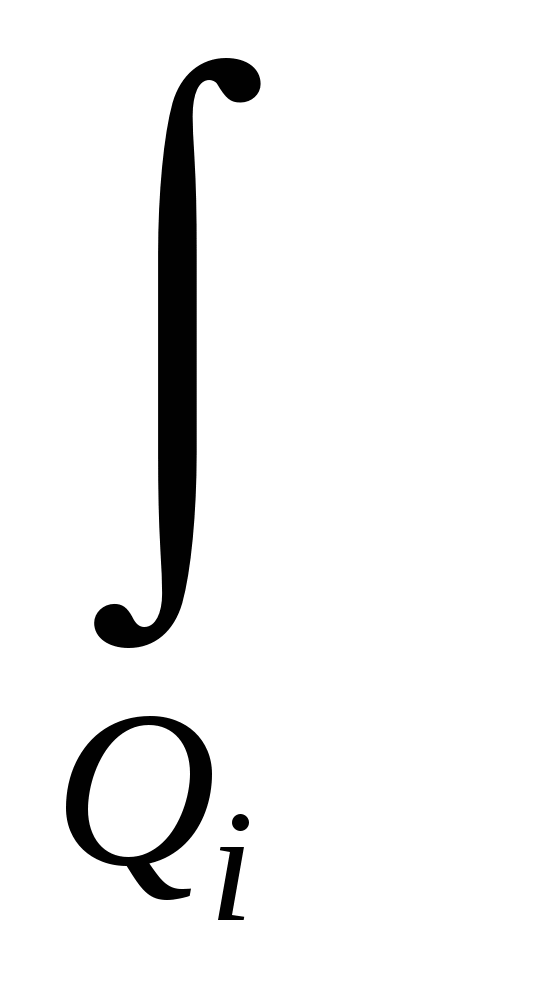 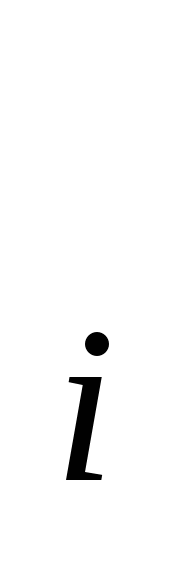 (…)dr = I(Q (…)dr = I(Q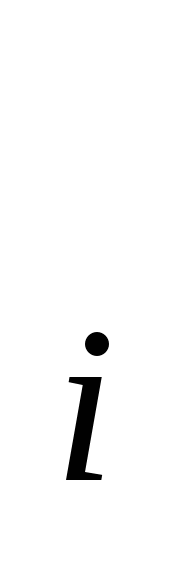 ). Надо понимать, что эти два соотношения являются необходимым и достаточным условием реализации программы в памяти ЭВМ, так как с одной стороны, мы задаём количество символов, которые надо преобразовать в памяти, а с другой стороны через вектор u(r) задаём правило выполнение требуемой команды на i-ом шаге. ППЭ есть отображение ). Надо понимать, что эти два соотношения являются необходимым и достаточным условием реализации программы в памяти ЭВМ, так как с одной стороны, мы задаём количество символов, которые надо преобразовать в памяти, а с другой стороны через вектор u(r) задаём правило выполнение требуемой команды на i-ом шаге. ППЭ есть отображение 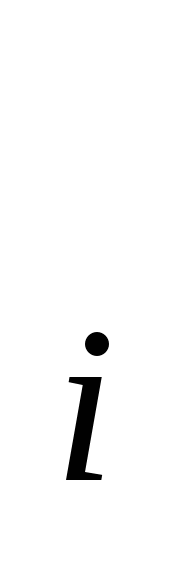 :U :U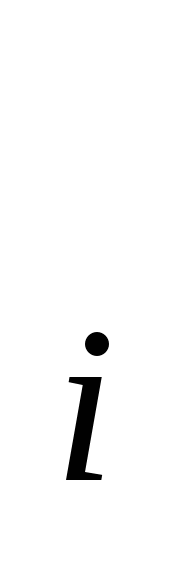 ×V ×V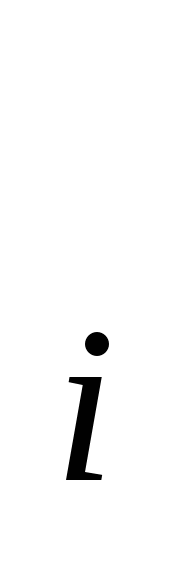 × RF, где область изменения производительности ПС, распределённой в пространстве и времени, а × RF, где область изменения производительности ПС, распределённой в пространстве и времени, а 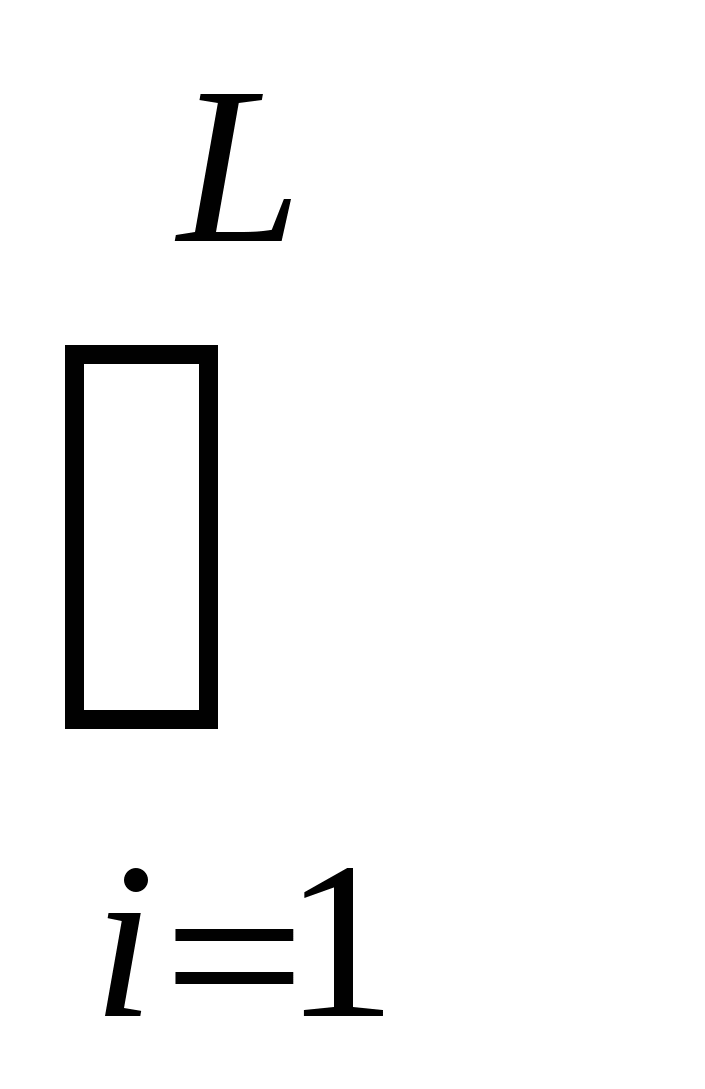 U U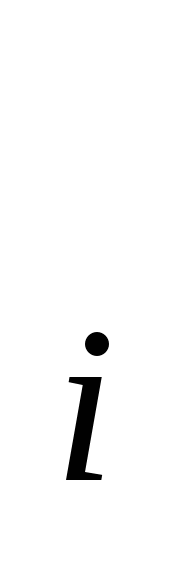 = U, = U, 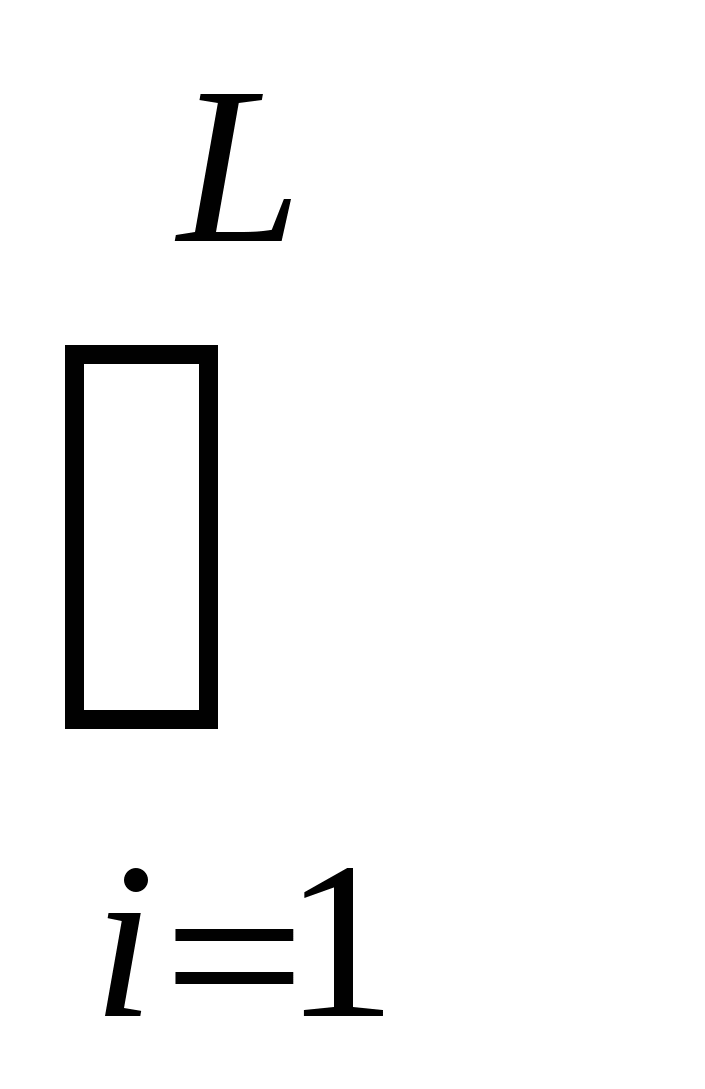 V V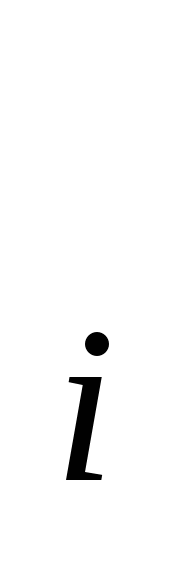 = V. = V.
При таком подходе требуемая потенциальная ЭП системы объединяет её ПВС и возможности в единое целое, направленные на достижение целевых установок, а разработчик системы получает инструмент для синтеза системы с требуемыми свойствами.
Известны два подхода к проектированию систем - это анализ и синтез.
При анализе (решение проблемы выбора) проектировщику выдают набор физических элементов и требуют предсказать возможный результата функционирования системы (некоторые выходные характеристики). То есть проектировщик сформирует один вариант системы, другой и так далее, анализирует результат функционирования каждого и выбирает тот вариант, который наиболее полно удовлетворяет требуемым условием.
При синтезе проектировщику дают набор выходных характеристик проектируемой системы и требуют определить количественный и качественный состав системы.
Для тех, кто достаточно глубоко изучал математику, между решением задачи Коши и краевой задачи для дифференциального уравнения такая же разница как между проблемой выбора и проблемой синтеза. То есть при анализе решается задача «от начала» и анализируется, что получится. При синтезе решается задача «от конца», желаемого результата; формируется система с требуемыми выходными характеристиками.
Синтез системы основан на установление разработчиком соответствия (условия замыкания) между моделью объекта в сложившейся ситуации и действием, изменяющим должным образом ситуацию в соответствии с предназначением системы. Изложим концепцию синтеза.
| |
|
|
 Скачать 1.48 Mb.
Скачать 1.48 Mb.