КБ (ответы). 1. Содержательная постановка задачи создание эвм, функционирующей в условиях разрушения программноаппаратной среды
 Скачать 1.48 Mb.
|
|
5.Анализ и синтез при создании ЭВМ. Концепция синтеза. Структура множества Q. КОНЦЕПЦИЯ СИНТЕЗА    Модель Системы ↔ Условие ЗАМЫКАНИЯ ↔ Модель Действия ЗАДАЧА. Дано. Множество возможных ситуаций (F×R). Множество возможных действий (R = X×T). Требуется определить. Условие замыкания. Потенциал поля эффективности (ППЭ) системы - (u(r),v(r),r) F; F- множество допустимых значений производительности; : U×V×RF. Количественно ситуация характеризуется результатом мгновенной деятельности системы ((u(r),v(r),r)r) на элементе r области Q. В случае рассмотрения ПС результат мгновенной деятельности системы будет характеризоваться    (…) dr. Руководствуясь разработанным автором законом сохранения целостности, получим условие ЗАМЫКАНИЯ, "собирая" по всей области Q "результаты" мгновенной деятельности системы,     Условие замыкания  (u(r),v(r),r)dr = I(Q), (2.2.)Модель действия Модель объекта Модель ситуации Результат замыкания Структура множества Q является носителем возможностей системы и механизмов их реализации. Соотношение (2.2.) является алгебраической операцией, определённым образом связанной со свойствами несущего множества. Как известно, алгебраическая операция это отображение, сопоставляющее всякому упорядоченному набору n элементов данного множества определённый элемент этого же множества. Отображение f(r):Q R обеспечивает формирование элементов r R, удовлетворяющих уравнению синтеза модели и способов применения системы (2.2.), т.е. формирование множества требуемых ПВС Q R). Физически эта операция "фильтрует" элементы множества R с целью выбора таких элементов, которые несут свойства создаваемой целевой системы и тем самым формируют элементы множества QR. Применительно к нашей задаче наша модель программы «фильтрует» состояния памяти ЭВМ с целью формирования в памяти ЭВМ требуемой логической последовательности команд и соответствующих состояний памяти. При этом надо понимать то, что такая «фильтрация» осуществляет управление внешними устройствами ЭВМ. | |
| | 6. Принцип системности. Задача А. Принцип системности. Для синтеза модели системы и способов ее использования, обладающей показателем ЭП I(Q), необходимо и достаточно задать множество Q R и функцию (...), удовлетворяющих условию (2.1.) А само соотношение (2.1.) целесообразно назвать уравнением синтеза, в общем случае с двумя неизвестными Q и (...). Это уравнение формализует закон сохранения целостности. Новая трактовка проблемы синтеза системы порождает новый класс задач, решение которых и обеспечивает одновременный синтез модели и способов применения системы. Задача А. Дано. Область из множества допустимых ПВС QR, множества допустимых состояний вектора возможностей V и вектора управления U, некоторое положительное значение показателя I(Q) (требуемое значение показателя ЭП). Требуется определить функцию (…), удовлетворяющую условию (2.1.). Комментарий А. В данной задаче при известных - логической последовательности команд, - количестве преобразованных в памяти символов, реализующих ПС, - множествах допустимых команд и ресурсов, - множестве допустимых правил выполнения команд, выбрать и обосновать требуемые команды и правила их выполнения, обеспечивающие требуемую производительность процессора. |
| | 7. Принцип системности. Задача Б. Задача Б. Дано. Множество допустимых ПВС R, функция (…), некоторое положительное некоторое положительное значение показателя I(Q). Требуется определить область из множества допустимых ПВС Q R, удовлетворяющую условию (2.1.) Комментарий Б. В данной задаче при известных - количестве преобразованных в памяти символов, реализующих ПС, - требуемых команд и ресурсов, - требуемых допустимых правил выполнения команд, выбрать и обосновать логическую последовательность выполнения команд. |
| | 8. Принцип системности. Задача В. Задача В. Дано. Область из множества допустимых ПВС Q R, множества допустимых состояний вектора возможностей V и вектора управления U, функция (…). Требуется определить вектор возможностей v(r) V и вектор управления u(r) U удовлетворяющих условию (u(r),v(r),r)dr   .Комментарий В. В данной задаче при известных - логической последовательности выполнения команд, - множестве допустимых команд и ресурсов, - множестве допустимых правилах выполнения команд, выбрать и обосновать требуемые команды и правила их выполнения, минимизирующие количество потребных преобразованных символов в памяти. |
| | 9. Принцип системности. Задача Г. Комментарий Г. В данной задаче при известных - логической последовательности выполнения команд, - множестве допустимых команд и ресурсов, - множестве допустимых правилах выполнения команд, выбрать и обосновать логическую последовательность команд, минимизирующих количество потребных преобразованных символов в памяти. Такой подход к синтезу позволил конструктивно определить, что должны содержать и давать исследователю методология, методы и технология моделирования системы. Методология должна содержать условия, определяющие свойства множества требуемых ПВС системы Q. Методы должны содержать условия, определяющие переход из одного состояние в другое на множестве требуемых ПВС системы Q. Технология должна содержать условия реализации переходов из одного состояние в другое на множестве требуемых ПВС системы Q Обычно система имеет определенный количественный состав, распределенный в пространстве с соответствующими зонами воздействия (влияния). Поэтому при непрерывном изменении времени условие (2.1.) будет задаваться в условиях формирования структуры системы и распределения функций между ее элементами при ограниченном количественном составе системы следующим образом. (Множество G) |
| | 10.Теория подобия при синтезе модели ЭВМ В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта. В настоящее время распространены методы машинной реализации исследования характеристик процесса функционирования больших систем. Для реализации математической модели на ЭВМ необходимо построить соответствующий моделирующий алгоритм. При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы S во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование — наиболее эффективный метод исследования больших систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования. Когда результаты, полученные при воспроизведении на имитационной модели процесса функционирования системы S, являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей статистической обработкой информации и целесообразно в качестве метода машинной реализации имитационной модели использовать метод статистического моделирования. Первоначально был разработан метод статистических испытаний, представляющий собой численный метод, который применялся для моделирования случайных величин и функций, вероятностные характеристики которых совпадали с решениями аналитических задач (такая процедура получила название метода Монте-Карло). Затем этот прием стали применять и для машинной имитации с целью исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, т. е. появился метод статистического моделирования. |
| | 11.Синтез модели и способов её применения, осложненный конфликтной ситуацией. Объект различной физической природы функционирует в како-то среде или вступает с другим объектом в определённые отношения. Поэтому, разрабатывая теорию моделирования функционирования сложных объектов, следует предположить, что в исследуемом процессе принимают участие как минимум две стороны (А, Б). Их взаимодействие рассматривается как конфликт с несовпадающими, в общем случае, интересами. По проблеме конфликта опубликовано значительное количество научных работ, монографий. Однако единого общепринятого определения конфликта не существует. Конфликт следует рассматривать не как синоним конфронтации, а как способ преодоления противоречий, форму взаимодействия сложных систем. Конфликт возникает при столкновении интересов, при желании сторон занять несовместимые позиции и т. п.. По нашему мнению при столкновении интересов надо искать пути преодоления возникшего конфликта, а не отстаивать некоторую позицию, позволяющую (теоретически) достичь поставленную цель. В настоящей работе рассмотрен подход к разрешению конфликта с позиции закона сохранения целостности объекта. Это позволило сформулировать "Принципа системности". В известных публикациях отсутствует формализованное определение системы. Как раз предлагаемый "принцип системности" позволил разработать инструмент разрешение конфликта. Структурная схема процесса разрешения конфликта между субъектами "А"и"Б" представлена на рис. 4.1. Субъект под воздействием среды формирует в соответствии со своим предназначением интересы. Для их обеспечения (отстаивания) создает систему. Система может создаваться для отстаивания экономических интересов, завоевания рынков сбыта, территорий для разработки полезных ископаемых, экологического мониторинга и управления экологической обстановкой, завоевания рынка сбыта информационных услуг, обеспечения информационной безопасности и других интересов. Примеры разработки моделей таких систем будут рассмотрены в дальнейшем. Исходя из интересов субъектом ставится цель. Цель достигается за счет разработки, развертывания и применения соответствующей системы, показатель эффективности функционирования которой, является мерой соответствия своему целевому предназначению. Ядро конфликта содержит механизмы формирования меры соответствия своего целевого предназначения. Так как на практике важно исследовать сложные динамические процессы, то для получения количественных характеристик целесообразно использовать подходы теория дифференциальных игр. При этом надо понимать, что в силу своей неполноты, эта теория позволяет лишь определять условия перехода системы из одного состояния в другое (методы), а полноту можно обеспечить только разработанная методология. Только эта теория позволяет определить свойства множеств требуемых ПВС разрабатываемой системы, задать сами эти множества. Не нарушая общности рассуждений, рассмотрим противостояние двух сторон "A" и "Б", обладающих определенными подсистемами.  |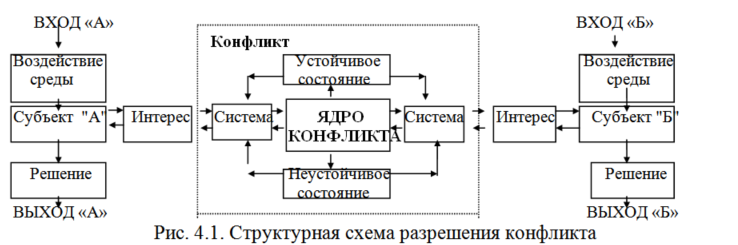
| | 12.Структурная схема взаимодействия трёх базовых подсистем при разрешении конфликта. Не нарушая общности рассуждений, рассмотрим противостояние двух сторон "A" и "Б", обладающих определенными подсистемами. 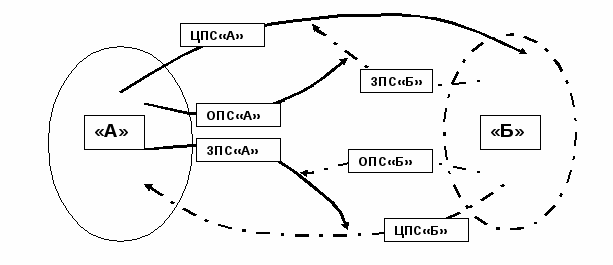 Рис. 4.2. Структурная схема взаимодействия трёх базовых подсистем при разрешении конфликта. Система должна выполнять три основных функции: 1. Целевую. 2. Защитную. 3. Обеспечивающую. Дальнейшее наращивание количественного состава новых функций приведёт к появлению подобных по содержанию функций. Поэтому правомерно предположить, что сторона "А" создает следующие подсистемы, выполняющие перечисленные три функции (рис.4.2): - Целевую подсистему (ЦПС"А"), - Защитную подсистему (ЗПС"А"), - Обеспечивающую подсистему (ОПС"А"), защищающую Целевую подсистему"А"от воздействия защитной подсистемы стороны "Б". ЦПС"А" предназначена для решения целевых задач на соответствующем множестве ПВС. ЗПС"А", предназначена для недопущения решения целевых задач ЦПС"Б" на общем со стороной "А" целевом множестве. Если рассматривать функции ЦПС"А" и ЗПС"А", то они находятся в противоречии, так как выполняют две противоречивые функции. Для гармоничного их существования, естественно предположить существование подсистемы, снимающей это противоречие. Возможности, механизмы их реализации, виды, способы, действий ОПС"А" определяются по схеме (рис.4.3.) через требуемый вклад в решение общей задачи ЦПС"А".   Целевая система А Целевая подсистемаА” ОбеспечивающаяпдсистемаА” Защитная система “A” ««Ф№  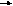         Оценивание    Действия Эффективность применения Возможности (Модель действия) (Модель системы)    Общая задача, решаемая целевой системой А Рис. 4.3. Схема взаимосвязи основных подсистем системы "А". Рассмотрим механизмы действия этих трёх функций. В соответствии с нашим подходом ПВС ПС удовлетворяют алгебраической операции, связанной со свойствами несущего множества вида (u(r),v(r),r)dr = I(Q). В случае действия противостоящей стороны, например «Б» происходит разрушение множества Q на величину ∆ Q. Естественно это приводит и к изменению I на величину ∆I, так как тогда  (u(r),v(r),r)dr = I(Q) -∆I. Для нейтрализации процесса разрушения памяти мы поступим следующим образом. |
| | |