Курсач приборы. Курсовая работа по дисциплине Теплотехнические измерения и приборы
 Скачать 304.74 Kb. Скачать 304.74 Kb.
|
Расчет расходной диафрагмыДля измерения расхода среды используются дроссельные диафрагмы без предварительной градуировки в трубопроводах круглого сечения с диаметром не менее 50 мм при значениях m от 0,05 до 0,64 в случае наличия определенной длины прямых участков до и после диафрагмы. Схема установки в трубопроводе наиболее простого сужающего устройства (СУ) – диафрагмы - в виде тонкого диска с круглым отверстием посредине и изображение характера потока представлены на рисунке 2.1. Там же дано распределение статического давления р по длине струи. Сжатие потока начинается перед диафрагмой и благодаря действию сил инерции достигает наибольшей величины на некотором расстоянии за ней, после чего струя вновь расширяется до полного сечения трубопровода. Перед диафрагмой и за ней в углах образуются зоны с вихревым движением, причем зона вихрей после диафрагмы более значительна, чем до нее. Давление струи около стенки трубопровода (сплошная линия) несколько возрастает за счет подпора перед диафрагмой и понижается до минимума за диафрагмой в точке наибольшего сужения струи, где сечение потока меньше, чем отверстие диафрагмы [3]. Далее по мере расширения струи давление около стенки снова повышается, но не достигает прежнего значения на величину рп ввиду наличия безвозвратных потерь на завихрение, удар и трение. Изменение давления струи по оси трубопровода практически совпадает с изменением давления около его стенки, за исключением участка перед диафрагмой и непосредственно в ней, где давление потока по оси трубы понижается (пунктирная линия). Жидкость должна заполнять все сечение, фазовое состояние ее не должно изменяться. Диафрагма должна быть выбрана таким образом, чтобы при всех значениях ожидаемого расхода среды коэффициент расхода был величиной постоянной. Минимальное значение критерия Re, при дальнейшем росте которого коэффициент расхода остается постоянной величиной, называется предельным значением критерия Рейнольдса. При минимальном расходе среды значение критерия Рейнольдса Re должно быть больше Reпред. Диафрагма представляет собой тонкий диск, имеющий круглое отверстие d20, центр которого должен совпадать с центром сечения трубы. 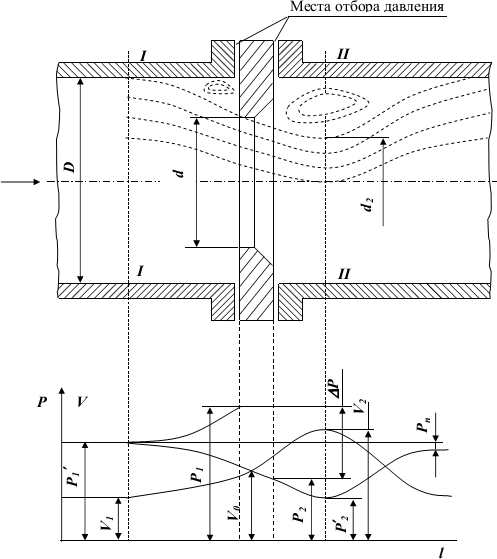 Рисунок 2.1. Характер потока и распределение статического давления в трубопроводе при установке сужающего устройства Диаметр отверстия диафрагм независимо от способа отбора представлен следующим соотношением : d20 ≥12,5 мм В тех случаях, когда толщина b ≤ 0,02 d20 можно изготовлять диафрагму без конического расширения к выходу потока. 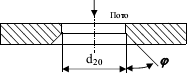 По толщине диафрагмы b > 0,02 d20 цилиндрическое отверстие должно выполняться с коническим расширением к выходу потока и углом наклона 30о ≤ φ ≤ 45о Отверстие диафрагмы цилиндрической формы со стороны входа потока имеет прямоугольную острую кромку. Длина цилиндрической части отверстия должна находиться в пределах : 0,005D20 ≤ l ≤ 0,02D20 Требования к изготовлению и установке, методика расчета СУ изложены в ГОСТ8.563.1-97 «Измерение расхода и количества жидкостей и газов методом переменного перепада давления» (РД50- 213-80, правила 28-64, 27-54), введенного с 01.01.99 г. При изготовлении и установке стандартных СУ в трубопроводах должны соблюдаться определенные требования, несоблюдение которых существенно влияют на погрешность измерения расхода. Допустимые диапазоны значений внутренних диаметров трубопроводов при температуре t = 20 оС и относительных площадей диафрагм mдолжны находиться в пределах: · для диафрагм с угловым способом отбора Δp (Рисунок 2.2): 50 мм ≤ d20 ≤ 1000 мм 0,05 ≤ m ≤ 0,64 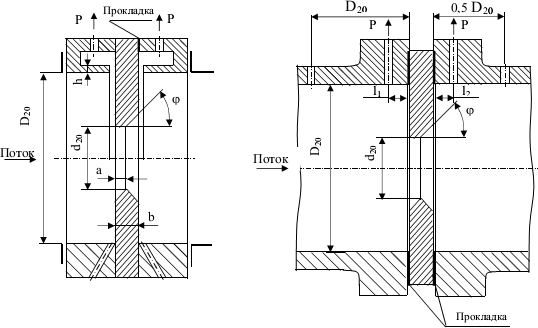 Рисунок 2.2 Угловой способРисунок 2.3 Фланцевый и трехрадиусный способ · способ отбора Δp для диафрагм с фланцевым и трехрадиусным способом отбора Δp (Рисунок 2.3): 50 мм ≤ D20 ≤ 760 мм 0,05 ≤ m ≤ 0,56 Расчет дроссельного устройства Расчет сужающего устройства заключается в определении его диаметра, при этом должны быть выполнены следующие условия: · стандартный максимальный перепад давления выбирается как можно больший (обеспечивается постоянство коэффициента α); · стандартный минимальный перепад давления выбирается как можно меньший (для снижения безвозвратных потерь давления); · модуль диафрагмы удовлетворяет условию: 0,05≤ m ≥0,7; · погрешность расчета составляет ±0,1%. Диафрагма должна быть выбрана таким образом, чтобы при всех значениях ожидаемого расхода среды коэффициент расхода α был величиной постоянной. 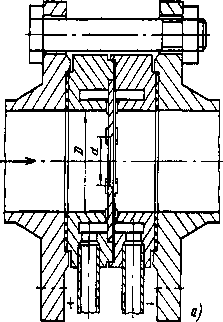 Рисунок 2.4. Установка камерной диафрагмы в трубопроводе типа ДК В камерной диафрагме давления к дифманометру передаются посредством двух кольцевых уравнительных камер, расположенных в ее корпусе перед и за диском с отверстием, соединенным с полостью трубопровода двумя кольцевыми щелями или группой равномерно расположенных по окружности радиальных отверстий (не менее четырех с каждой стороны диска). Кольцевая камера перед диском называется плюсовой, а за ним — минусовой. Наличие у диафрагмы кольцевых камер позволяет усреднить давление по окружности трубопровода, что обеспечивает более точное измерение перепада давления. Точность измерения расхода при помощи диафрагм зависит от степени остроты входной кромки отверстия, влияющей на значение коэффициента расхода α. Кромка не должна иметь скруглений, заусенцев и зазубрин. При d20 < 125 мм она должна быть настолько острой, чтобы луч света не давал от нее отражения. Допускаемое смещение оси отверстия сужающих устройств относительно оси трубопровода не должно превышать (0,5—1) мм. Для изготовления проточной части диафрагм и сопел применяются устойчивые к коррозии и эрозии материалы (нержавеющая сталь, латунь или бронза). На ободе сужающего устройства или на прикрепленной маркировочной пластинке обычно наносятся: обозначение типа устройства и заводской номер; диаметры d20 и D20; стрелка, указывающая направление потока; марка материала; знаки + и — соответственно со стороны входа и выхода потока. К сужающему устройству прилагается выпускной аттестат, в котором указываются: · наименование и расчетные параметры измеряемой среды; величины, полученные при расчете сужающего устройства (m, α, ε, d20 и др.); · формула, по которой проверялась правильность расчета; · основные характеристики сужающего устройства и дифманометра. Основная погрешность диафрагм и сопл составляет ±(0,6— 2,5)%. С повышением значения m она увеличивается, а с ростом диаметра трубопровода D20 — уменьшается. К расходомерам, применяемым в различных технологических процессах выдвигаются повышенные требования: высокая точность измерений, независимость показаний расходомеров от давления и температуры, расширение диапазонов измерения, повышение безотказности в работе и сроков службы. Минимальной значение критерия Re, при дальнейшем росте которого коэффициент расхода α остается постоянной величиной, называется предельным значением критерия Рейнольдса [4]. Исходные данные к работе: · измеряемая среда – газ природный дашавский, · температура среды – 301 ºС, · максимальный расход – 2098 кг/ч, · минимальный расход – 2000 кг/ч, · максимальное давление – 9 МПа, · минимальное давление – 8,97 МПа, · материал – сталь марки X23H13. Расход среды может быть задан в единицах массы G - кг/сек или в единицах объема Q –м3/сек. Расчетные формулы для определения расхода среды имеют вид: 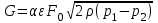 , (2.1) , (2.1)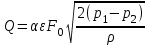 (2.2) (2.2)где α - коэффициент расхода; ε - поправочный коэффициент на расширение среды (для газообразных сред); Fо - площадь проходного сечения диафрагмы, м2; ρ - плотность среды перед диафрагмой, кг/м3; p1-p2= Δp - перепад давления на диафрагме, Па. 1. По величине максимального расхода определяется внутренний диаметр трубопровода по формуле: 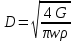 (2.3) (2.3)где w - средняя скорость среды в трубопроводе, м/с. Значения средней скорости потоков для расчета трубопроводов даны в таблице 2.1. Исходя из данных таблицы 2.1, принимаем скорость w=75 м/с. Таблица 2.1 Значение средней скорости ԝ потоков для расчета трубопроводов
Из справочных данных значение плотности при данной температуре (180°С) составит ρ=4,365 кг/м3. 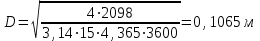 , (2.4) , (2.4)По подсчитанному значению диаметра выбирается ближайший стандартный диаметр из таблицы 2.2. Рассчитанному значению подойдет внутренний диаметр, величина которого 98 мм. 2. Выбираем расчетную величину расхода, которая соответствует максимальному расходу : G = 2098 кг/ч (из исходных данных) Таблица 2.2 Значение стандартных диаметров трубопроводов
1. Определяем значение критерия Рейнольдса для принятого расчетного расхода из выражения: 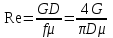 (2.5) (2.5)где f - площадь сечения трубопровода, м2; μ – динамический коэффициент вязкости, Па∙с. Для горючего газа и воздуха динамический коэффициент вязкости приведен в таблице 2.3, для воды и водяного пара - в таблице 2.4. Таблица 2.3 Физические параметры горючих газов и воздуха
Таблица 2.4 Динамический коэффициент вязкости воды и водяного пара (µ·105 Па·с)
Примечание: над чертой - вода, под чертой - пар. При определении численных значений динамического коэффициента вязкости следует применять линейное интерполирование. В первом приближении можно считать, что динамический коэффициент вязкости не зависит от давления, а определяется лишь одной температурой. С помощью табличных данных (таблицы 2.3, 2.4) и метода интерполяции определяем значение динамического коэффициента вязкости. 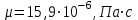 , при t =301 , при t =301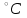 (2.6) (2.6)Отсюда получаем значение критерия Рейнольдса: 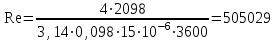 (2.7) (2.7)2. Выбираем максимальный расчетный перепад давления: Δp = p1 - p2 (2.8) Δp = 9 – 8,97 = 0,03 МПа (2.9) Если задана допустимая величина потери давления pд, то ориентировочно можно принять ∆p = 2pд. 3. Определяем диаметр трубопровода при рабочей температуре t по уравнению: D = D20 [1 + α0 (t - 20)] = D20Kt (2.10) где α0 - средний коэффициент линейного теплового расширения материала трубопровода; Kt - поправочный множитель на тепловое расширение (значения Kt приведены в таблице 2.5). С помощью метода интерполяции определяем коэффициент Kt при температуре 301 ºС для стали марки X23H13. K = 1,0045 + 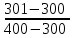 (1,0066 -1,0045) = 1,004521 (2.11) (1,0066 -1,0045) = 1,004521 (2.11)С учетом коэффициента Kt рассчитываем диаметр D: D = 98 ∙ 1,004521 = 98,4430 мм (2.12) 4. Диаметр расточки диафрагмы d определяем в следующей последовательности: а) подсчитываем значение mα из соотношения: mα = 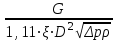 (2.13) (2.13)Таблица 2.5 Поправка на тепловое расширение трубопровода и диафрагм Kt
Величину ξ берут из таблицы 2.6 по подсчитанному значению ∆p/p1 принимая m=0,3 (в первом приближении). Сначала находим соотношение ∆p/p1: 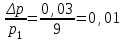 (2.14) (2.14)Затем методом интерполяции определяем значение ξ: ξ = 1 (2.15) Таблица 2.6 Значение поправочного множителя на расширение среды, ξ
Исходя из вышеприведенной формулы, вычисляем величину mα: mα = 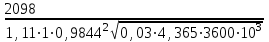 = 0,2841 (2.16) = 0,2841 (2.16)б) для найденного значения mα находят величину m. Для нахождения значения m по известной величине mα строим графическую зависимость mα = ƒ(m) при принятом значении D. Для этого по данным таблицы 2.7 берем четыре соответствующих значения m и mα, которые представлены в таблице 2.8, и строим график mα = ƒ(m) . Для определения значений mα проводим интерполяцию, так как диаметр трубопровода отличается от указанного в таблице (выбираем четыре точки так, чтобы две имели значение mα больше и две меньше, чем получилось при расчете по формуле). Таблица 2. 7 Зависимость произведения ma от m и D
По построенному графику определяют численное значение m. Величину m рекомендуется определять с числом значащих цифр, соответствующих погрешности порядка 0,1%. При mα = 0,284 значение m =0,425 в) определяем предварительное значение диаметра расточки диафрагмы при температуре 20°С из соотношения: d20 = 98 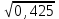 = 64 мм (2.17) = 64 мм (2.17)Таблица 2.8 Зависимость произведения mα от m
5. Определяем потерю напора в диафрагме при расчетном расходе из соотношения: 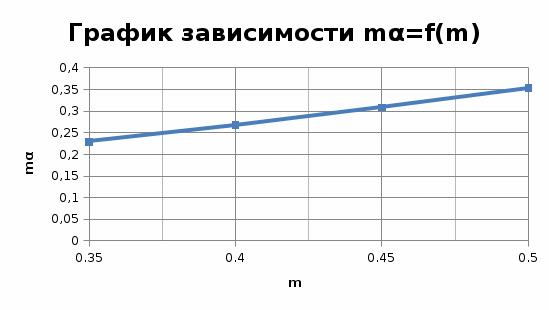 Рисунок 2.5. График зависимости mα=f(m) где К - коэффициент, являющийся функцией от m (см. таблицу 2.9). Таблица 2.9 Значения коэффициента К в зависимости от величины m
Применив метод интерполяции, получаем: K = 0,47 + 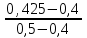 (0,57-0,47) = 0,495 (2.18) (0,57-0,47) = 0,495 (2.18)Таким образом, потеря напора в диафрагме составит: p = 0,495∙ 100000 = 49500 Па (2.19) 6. Проверка определения диаметра расточки отверстия диафрагмы d заключается в следующем: а) Из представленного ниже соотношения определяется коэффициент расхода: α = αuK1K2K3, (2.20) где αu – исходный коэффициент расхода ; К1 ‒ поправочный множитель, который вводится при значении Re меньше предельного; К2 ‒ поправочный множитель на относительную шероховатость труб; К3 ‒ поправочный множитель на неостроту входной кромки. б). Подсчитываем значение α. Для этого по расчетному значению m, пользуясь таблицей 2.10, определяем величину исходного коэффициента расхода αu с точностью не менее третьего знака (применяя интерполирование в промежутке). Таблица 2.10 Значение исходного коэффициента расхода au и предельные значения критериев Рейнольдса (Reпред)
αu = 0,66 + 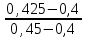 (0,676 - 0,66) = 0,668 (2.21) (0,676 - 0,66) = 0,668 (2.21)в). Определяем предельное значение критерия Рейнольдса: Reпред = 130000 + 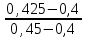 (160000 - 130000) = 131500 (2.22) (160000 - 130000) = 131500 (2.22)Так как предельное значение Re меньше рассчитанного (Reпред г). По таблице 2.11 определяем произведение К2К3, зависящее от уже известных величин m и D. При диаметре, равном 98 мм и m=0,425 получаем: K2K3 = 1,015 (2.23) α = 0,668 ∙ 1 ∙ 1,015 = 0,678 (2.24) Таблица 2.11 Произведение поправочных множителей К2К3, для нормальных диафрагм
д)Точное значение ξ определяем по известным значениям m и ∆P/Р1, пользуясь данными таблицы 2.6 (при приближенной оценке m принимался 0,3). Методом интерполяции получаем ξ = 1. ж) Исходя из полученных данных, вычисляем массовый расход по формуле: G * = G - 1,11αmξD2 G* = 2098 – (1,11 ∙ 0.678 ∙ 0,425 ∙ 1 ∙ 0,9844 2 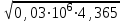 ) = 2050 ) = 2050 9.В таком случае погрешность составит: Δ = Δ = 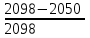 ∙ 100% = 2,2% (2.27) ∙ 100% = 2,2% (2.27)Если полученное значение расхода отличается от расчетной величины расхода в пределах ±0,5%, то расчет выполнен правильно. Если расхождение не превышает ±2%, допускается уточнить диаметр отверстия диафрагмы по уравнениям: При расхождении больше 2% расчет выполняется вновь. Наименьший расход, при котором не нужно вводить поправочный множитель К1, получим из выражения: Gmin = Gрасч Gmin = 2050 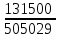 = 534 = 534 Вывод: Выполненный расчет расходной диафрагмы трубопровода показал, что погрешность расчета не превышает 2%, и равна ∆ = 2%, поэтому можно сделать заключение о том, что расчет выполнен корректно. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
