Курсовая работа_2. Курсовая работа. По предмету Статистика

• Название: Курсовая работа. По предмету Статистика
• Анкор: Курсовая работа_2.doc
• Дата: 20.09.2018
• Размер: 0.63 Mb.
• Имя файла: Курсовая работа_2.doc
• Тип: Курсовая; #24872
• Категория: Математика
• страница: 1 из 3

.Министерство транспорта Российской Федерации.

Московский автомобильно–дорожный институт

(Государственный технический университет).

Кафедра Экономики дорожного хозяйства.

Курсовая работа.
По предмету: «Статистика».

Проверил: Г.С. Беляков.


г. Москва.

2007 учебный год.

Задания на выполнение курсовой работы по дисциплине «Статистика».

Раздел 1. Ряды распределения.

1.1. Имеются данные о замерах часовой интенсивности движения автомобилей на автомагистрали.

1.2. По данным 100 наблюдений, начиная с № 8, выписать первоначальный ряд и ранжировать его в порядке возрастания значений признака.

1.3.Построить дискретный вариационный ряд.

1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.

1.5.Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).

1.6.Изобразить вариационный ряд графически в виде гистограммы, полигона, кумуляты и огивы.

1.7. Дать анализ полученных результатов.

Раздел 2. Статистические группировки.

2.1. Имеются данные о показателях деятельности 25 дорожно – строительных организаций.

2.2. С помощью аналитической группировки выявить характер взаимосвязи между результативным признаком «Объем СМР по сметной стоимости, тыс. руб.» и факторным признаком «Среднегодовая стоимость активной части ОПФ, тыс. руб.».

2.3. Построить поле корреляции и эмпирическую линию регрессии.

2.4.Рассчитать величины межгрупповой, средней из внутригрупповых и общей дисперсий.

2.5. Рассчитать величины коэффициента детерминации и корреляционного отношения.

2.6. Дать анализ полученных результатов.

Раздел 3. Ряды динамики.

3.1. Имеются данные о протяженности автомобильных дорог с твердым покрытием.

3.2.По данным за 9 лет, начиная с 1963 года рассчитать показатели динамики: абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста по годам (базисные и цепные).

3.3. Рассчитать обобщающие показатели динамического ряда: средний уровень ряда, средний абсолютный прирост, средние темпы роста и прироста.

3.4. Произвести аналитическое выравнивание ряда динамики по прямой с помощью метода наименьших квадратов.

3.5. С помощью полученного в результате выравнивания уравнения осуществить экстраполяцию на 1 шаг вперед.

3.6. Нанести на график фактические и выравненные уровни.

3.7. Дать анализ полученных результатов.

Раздел 1. Ряды распределения.

1.2. По данным 100 наблюдений, начиная с № 4, выписать первоначальный ряд и ранжировать его в порядке возрастания значений признака.

Первоначальный ряд.

№ п/п	Значение варианты, х	№ п/п	Значение варианты, х	№ п/п	Значение варианты, х	№ п/п	Значение варианты, х
1	15	26	8	51	4	76	10
2	12	27	9	52	9	77	8
3	13	28	18	53	9	78	2
4	5	29	11	54	7	79	10
5	11	30	10	55	8	80	10
6	13	31	14	56	7	81	10
7	9	32	9	57	5	82	2
8	4	33	5	58	5	83	10
9	3	34	9	59	7	84	8
10	6	35	5	60	6	85	11
11	3	36	4	61	5	86	5
12	8	37	10	62	2	87	4
13	10	38	7	63	3	88	5
14	9	39	12	64	10	89	3
15	21	40	7	65	6	90	10
16	22	41	16	66	2	91	10
17	26	42	16	67	10	92	6
18	28	43	9	68	10	93	2
19	31	44	21	69	3	94	10
20	6	45	13	70	9	95	10
21	3	46	8	71	5	96	4
22	13	47	3	72	9	97	3
23	19	48	10	73	4	98	6
24	9	49	7	74	11	99	3
25	7	50	4	75	4	100	4
						Итого:	877

Ранжированный ряд в порядке возрастания значений признака:

№ п/п	Значение варианты, х	№ п/п	Значение варианты, х	№ п/п	Значение варианты, х	№ п/п	Значение варианты, х
1	2	26	5	51	9	76	10
2	2	27	5	52	9	77	10
3	2	28	5	53	9	78	10
4	2	29	5	54	9	79	11
5	2	30	5	55	9	80	11
6	3	31	5	56	9	81	11
7	3	32	6	57	9	82	11
8	3	33	6	58	9	83	12
9	3	34	6	59	9	84	12
10	3	35	6	60	9	85	13
11	3	36	6	61	9	86	13
12	3	37	6	62	9	87	13
13	3	38	7	63	10	88	13
14	4	39	7	64	10	89	14
15	4	40	7	65	10	90	15
16	4	41	7	66	10	91	16
17	4	42	7	67	10	92	16
18	4	43	7	68	10	93	18
19	4	44	7	69	10	94	19
20	4	45	8	70	10	95	21
21	4	46	8	71	10	96	21
22	4	47	8	72	10	97	22
23	5	48	8	73	10	98	26
24	5	49	8	74	10	99	28
25	5	50	8	75	10	100	31
						Итого:	877

1.3.Построить дискретный вариационный ряд.

№ п/п	Значение варианты, х	Частота, f	№ п/п	Значение варианты, х	Частота, f
1	2	5	13	14	1
2	3	8	14	15	1
3	4	9	15	16	2
4	5	9	16	18	1
5	6	6	17	19	1
6	7	7	18	21	2
7	8	6	19	22	1
8	9	12	20	26	1
9	10	16	21	28	1
10	11	4	22	31	1
11	12	2	23	Итого:	100
12	13	4

1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.

Для начала определим число интервалов по формуле Стержеса.

n = 1 + 3,322∙lgN, где n – число интервалов, N – общее число единиц совокупности.

n = 1 + 3, 322∙2 = 7,644

Исходя из этого, будем рассматривать интервальный ряд с количеством интервалов 6, 7 и 8. Величину интервала определим по формуле:



Тогда величина интервала для интервального ряда с 5 интервалами равна 5,8, с 6 интервалами – 4,83, с 7 интервалами – 4,14, c 8 интервалами – 3,63.

№ п/п	Значение интервала	Частота, f			№ п/п	Значение интервала	Частота, f
1	2 - 7.8	44			1	2 – 6.83	37
2	7.8 - 13.6	44			2	6.83 – 11.66	44
3	13.6 - 19.4	6			3	11.66 – 16.49	10
4	19.4 - 25.2	3			4	16.49 – 21.32	4
5	25.2 - 31	3			5	21.32 – 26.15	2
	Итого:	100			6	26.15 – 31	2
						Итого:	100

№ п/п	Значение интервала	Частота, f
1	2 – 6,14	37
2	6,14 – 10.28	41
3	10.28 – 14.42	11
4	14.42 – 18.56	4
5	18.56 – 22.7	4
6	22.7 – 26.84	1
7	26.84 – 31	2
	Итого:	100

№ п/п	Значение интервала	Частота, f
1	2 – 5.63	31
2	5.63 – 9.26	31
3	9.26 – 12.89	22
4	12.89 – 16.52	8
5	16.52 – 20.15	2
6	20.15 – 23.78	3
7	23.78 – 27.41	1
8	27.41 – 31	2
	Итого:	100

По полученным данным видно, что наиболее лучший вариант группировки – это интервальный вариационный ряд с 5 интервалами, так как прослеживается тенденция в уменьшении частот, а так же отсутствие интервалов с нулевыми частотами.

№ п/п	Значение интервала	Центр интервала	Частота, f	Накопленная частота
1	2 – 7,8	4,9	44	44
2	7,8 – 13,6	10,7	44	88
3	13,6 – 19,4	16,5	6	94
4	19,4 – 25,4	22,4	3	97
5	25,4 – 31	28,1	3	100

1.5.Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).

Среднеарифметическая взвешенная.

Дискретный вариационный ряд.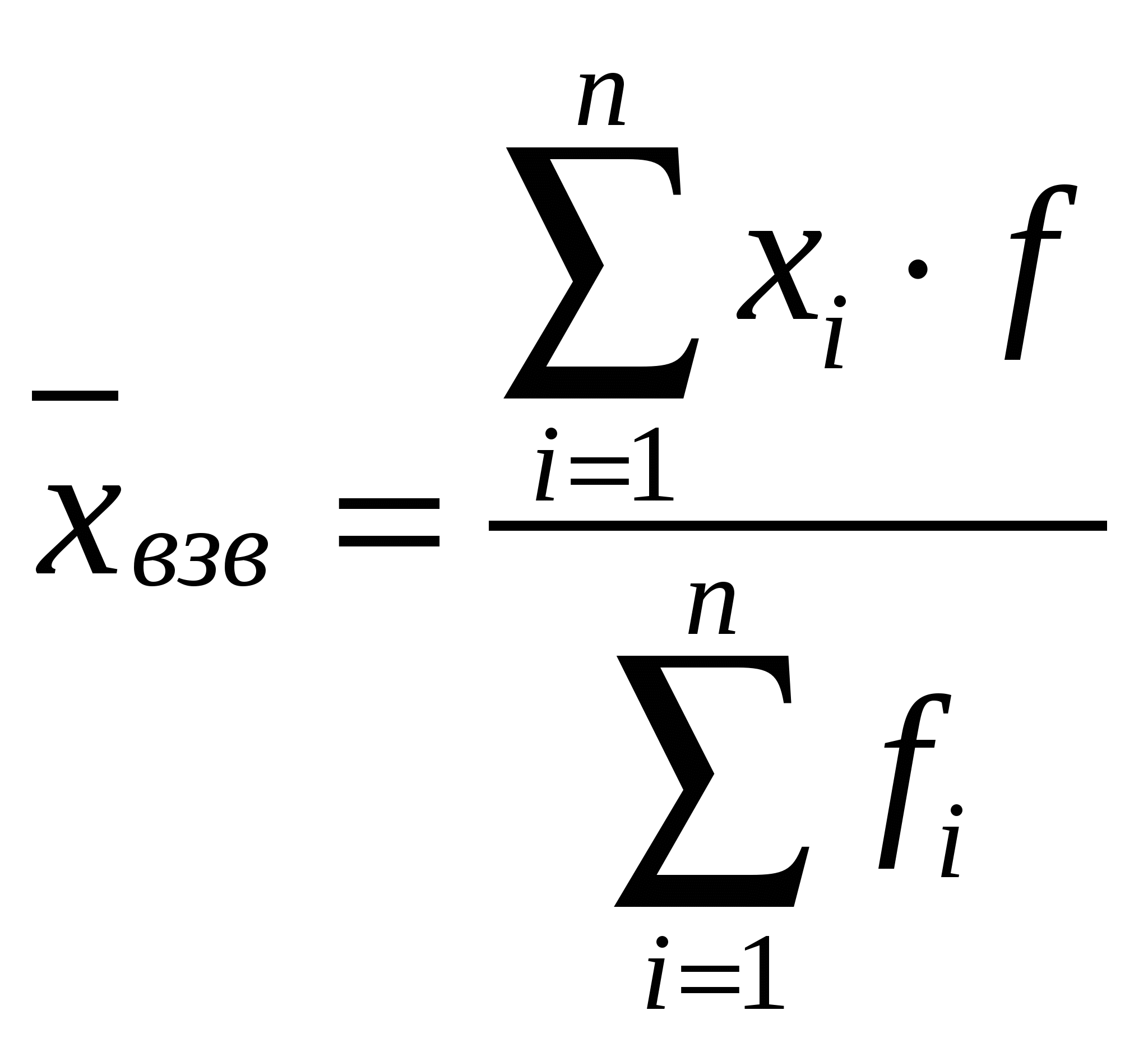

, где

Σx_i∙f_i – сумма произведений значений признака и их частот;

Σf_i – сумма всех частот.

χ _{взв = 882/100=8,82}

Интервальный вариационный ряд.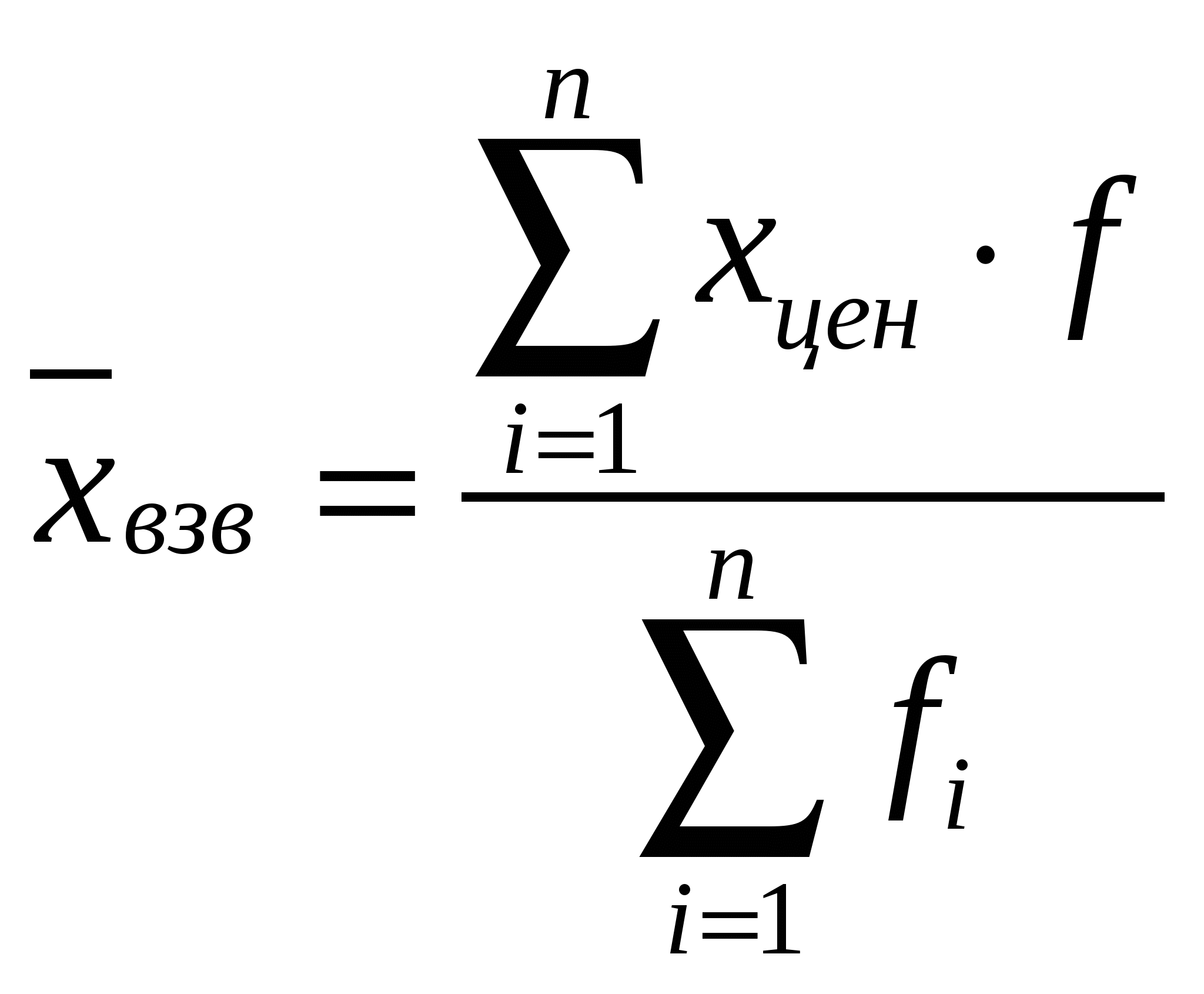

, где

Σx_цен∙f_i – сумма произведений центров интервалов и их частот;

Σf_i – сумма всех частот.

χ _{взв = 963,52/100=9,64}

Мода.

Дискретный вариационный ряд.

Это вариант имеющий наибольшую частоту f.



Интервальный вариационный ряд.

, где

х₀ – нижняя граница модального интервала;

i₀ – величина модального интервала;

f₁, f₂, f₃ – частота интервала предшествующего, модального и следующего за модальным.

М_{0 = 2+5,8*((44-0)/(44-0)-(44-44))=7,8}

Медиана.

Дискретный вариационный ряд.

Это вариант стоящий в центре ранжированного ряда.



Интервальный вариационный ряд.

, где

х₀ – нижняя граница медианного интервала;

i₀ – величина медианного интервала;

Σf_i – сумма всех частот;

S_{(Me – 1)} – сумма накопленных частот интервалов, предшествующих медианному;

f_Me – частота медианного интервала.

Размах вариации.

Дискретный вариационный ряд.