Курсовая работа_2. Курсовая работа. По предмету Статистика
 Скачать 0.63 Mb.
|
R=31 –2 = 29Интервальный вариационный ряд. R = 31 – 2 = 29Среднее линейное отклонение. Дискретный вариационный ряд. 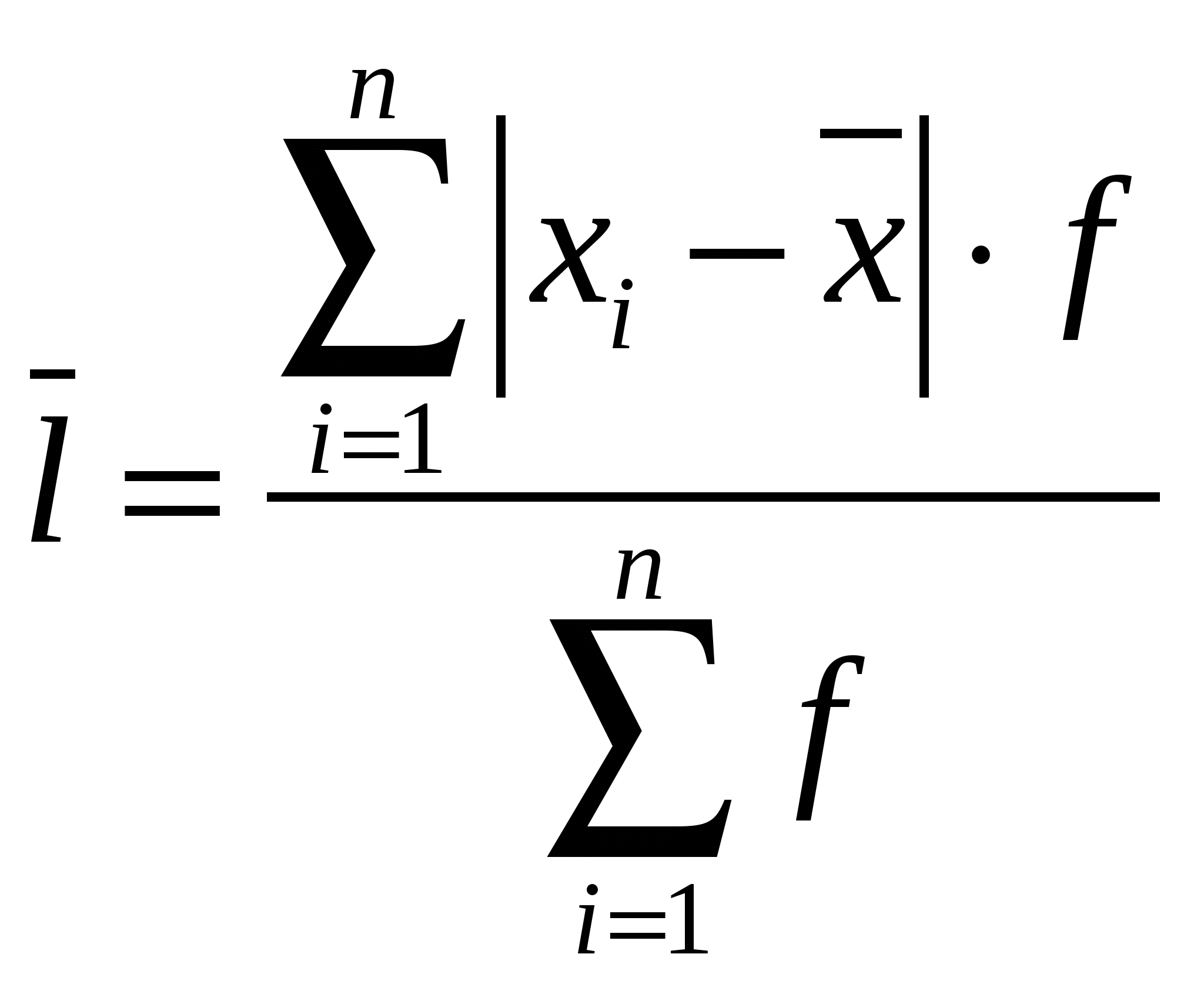 l = (19,18+17,18+13,18+12,18+10,18+9,18+ 4,36+6,18+5,18+16,72+6,36+8,72+18,88+ 2,16+4,92+12,74+16,92+34,38+43,38+46,56+34,1)/100 = 374,82/100 = 3,75 Интервальный вариационный ряд. 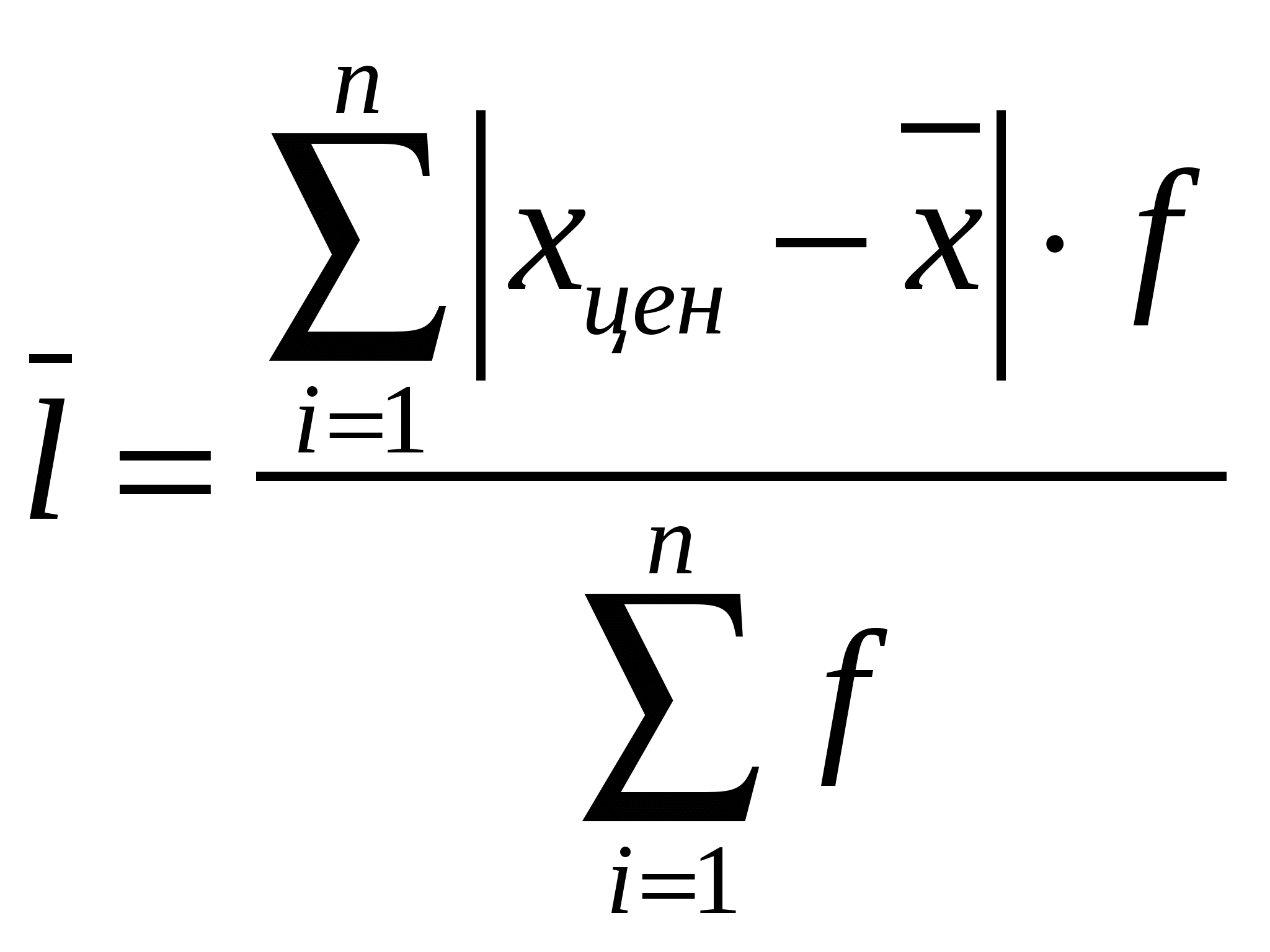 l = (172,48+82,72+46,08+40,74+57,84)/100 = 399,86/100 = 3,99 Дисперсия (средняя квадратов отклонений). Дискретный вариационный ряд. 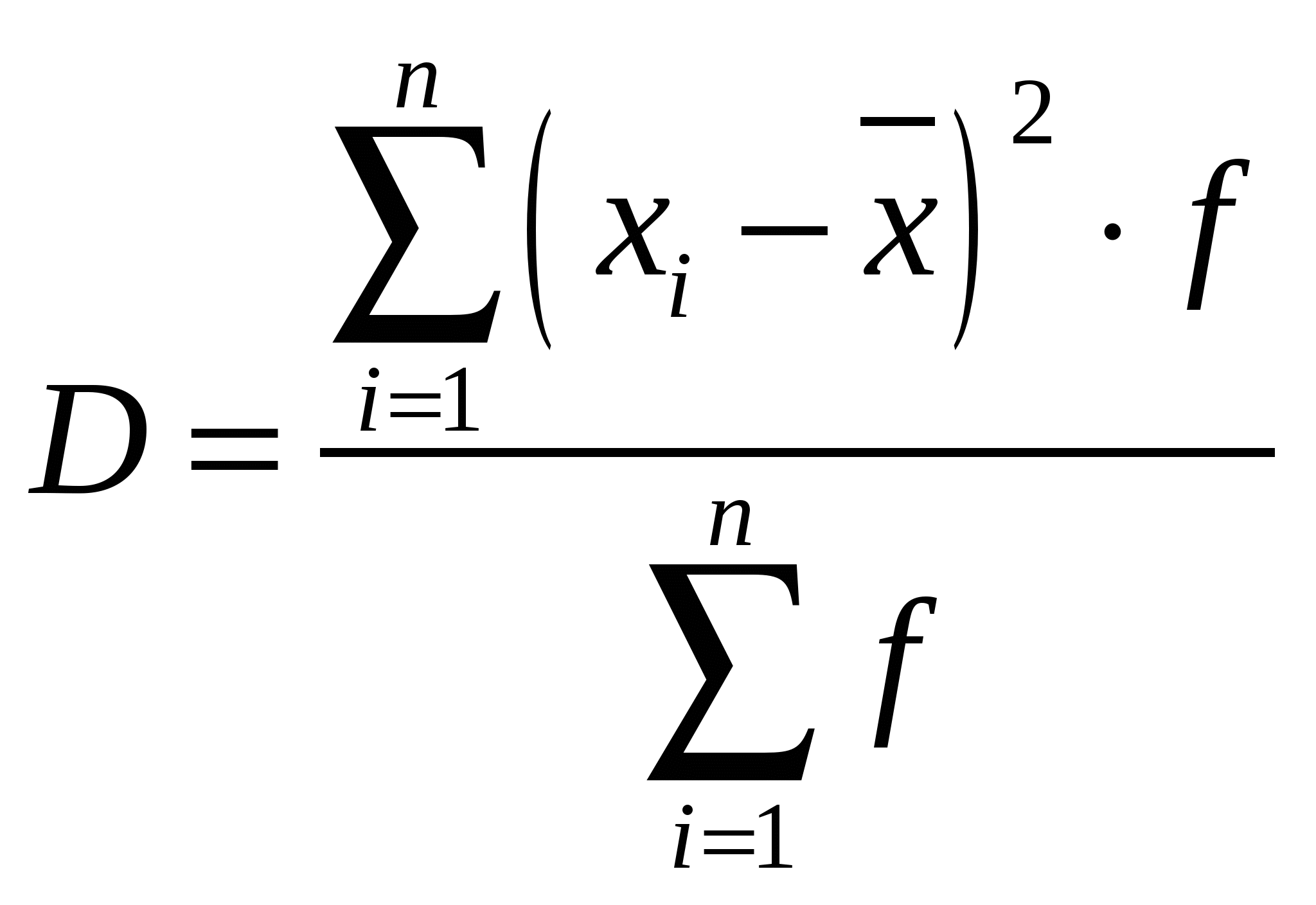 D = (232.56+270.98+209.09+131.33+47.7+ 23.19+4.03+0.39+22.28+19+20.22+26.83+38.19+103.1+84.27+103.63+148.35+173.7+295.15+367.87+491.95)/100=2813.81/100=28.14 Интервальный вариационный ряд. 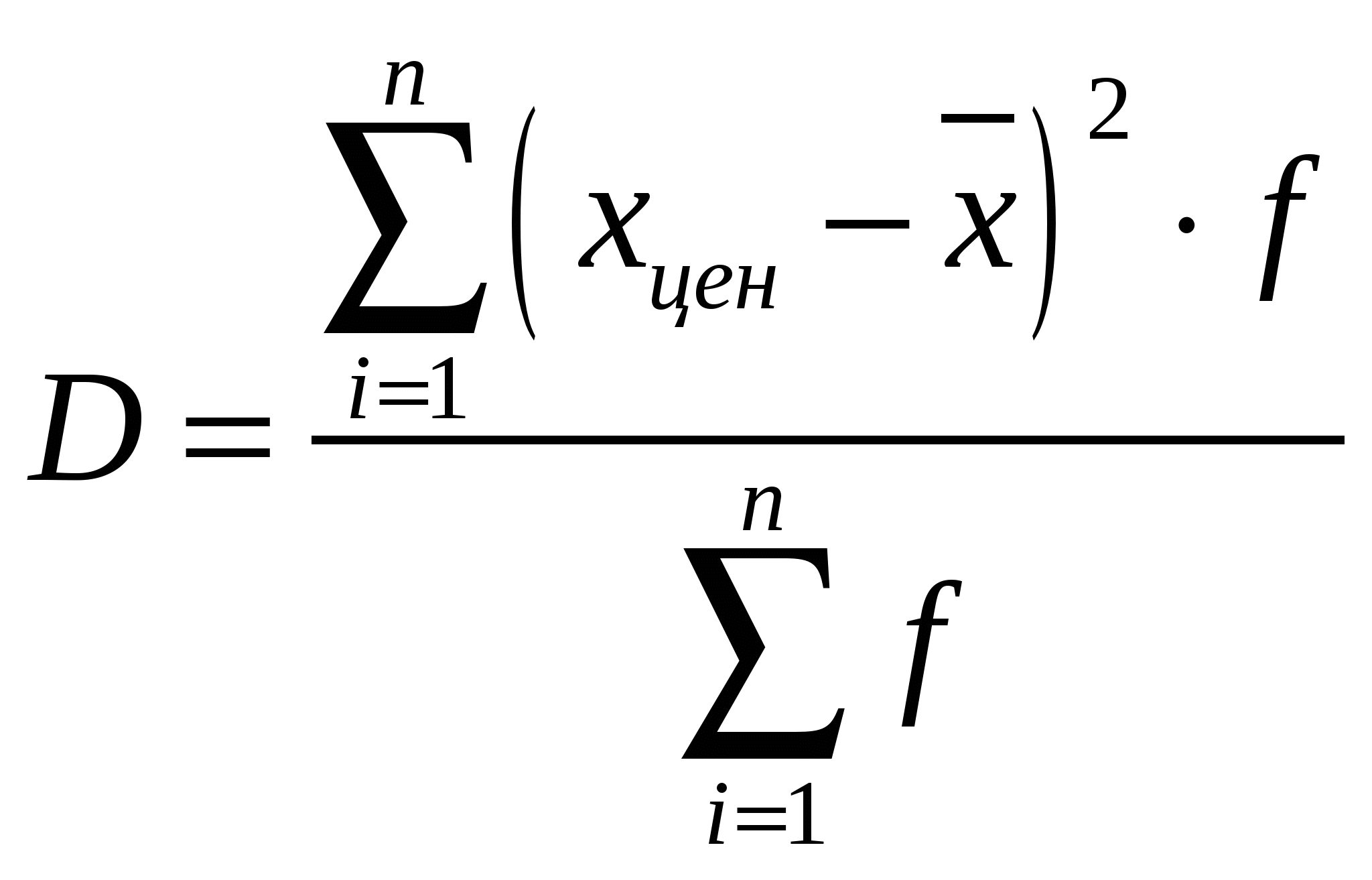 D = (672.12+155.5+353.89+553.25+1115.16)/ 100=2853.92/100=28.54 Среднее квадратическое отклонение.  Дискретный вариационный ряд. σ=√28.14=5.30 Интервальный вариационный ряд. σ=√28.54=5.34 Коэффициент вариации. 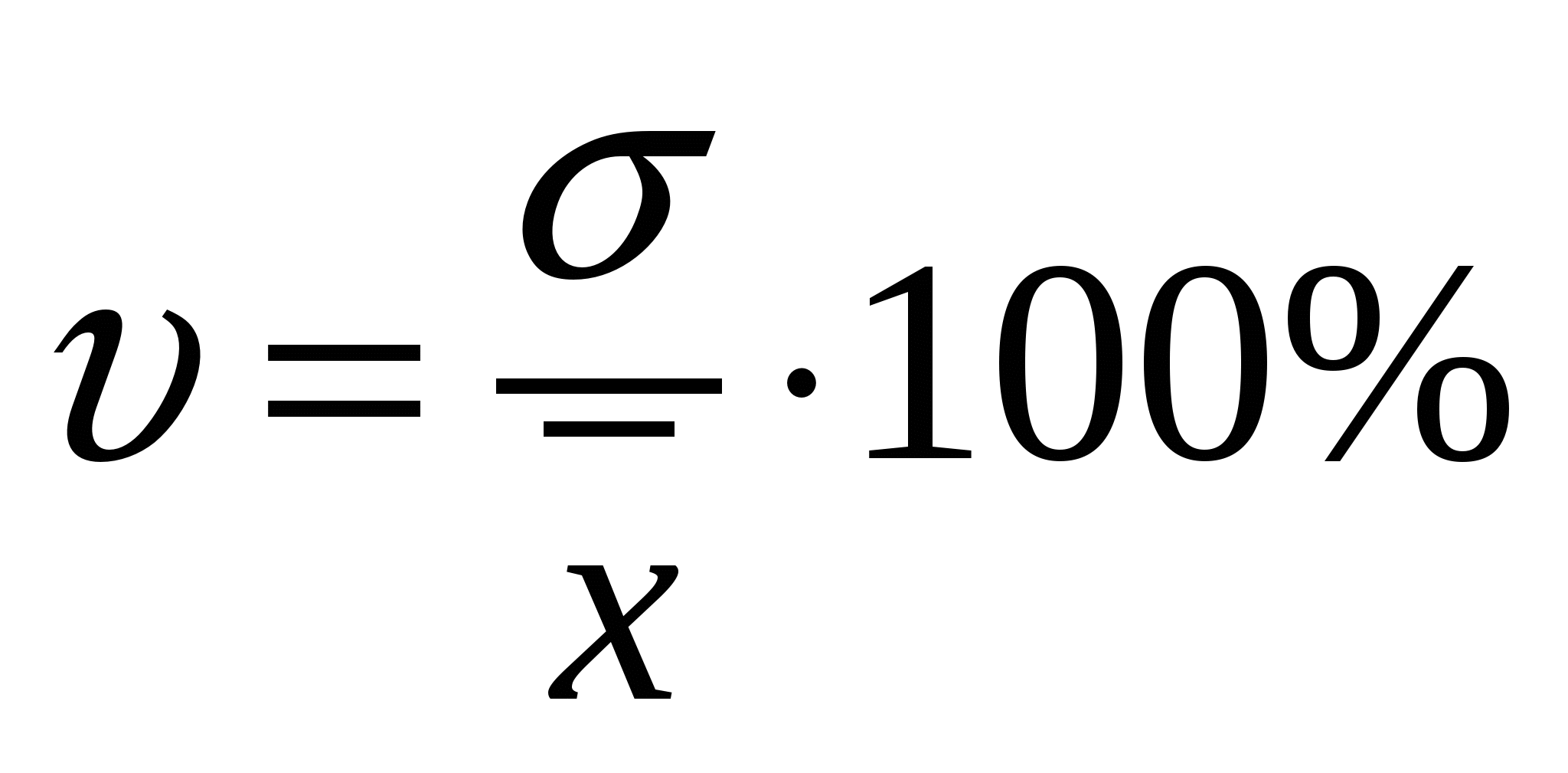 Дискретный вариационный ряд. υ=(5.30/8.82)*100%=60.09% Интервальный вариационный ряд. υ=(5.34/8.82)*100%=60.54% 1.6.Изобразить вариационный ряд графически в виде гистограммы, полигона, кумуляты и огивы. Гистограмма. 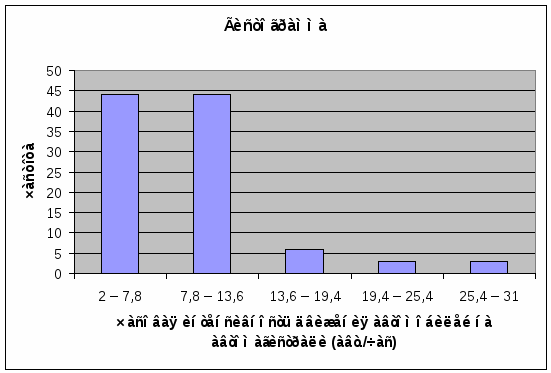 Полигон. 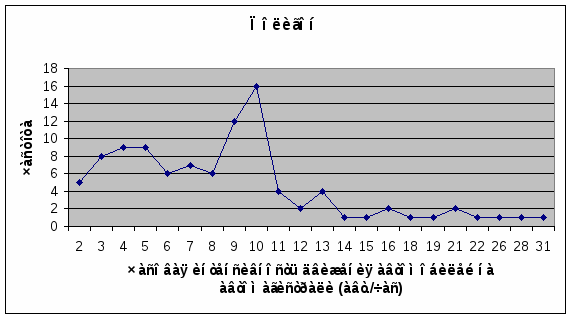 Кумулята 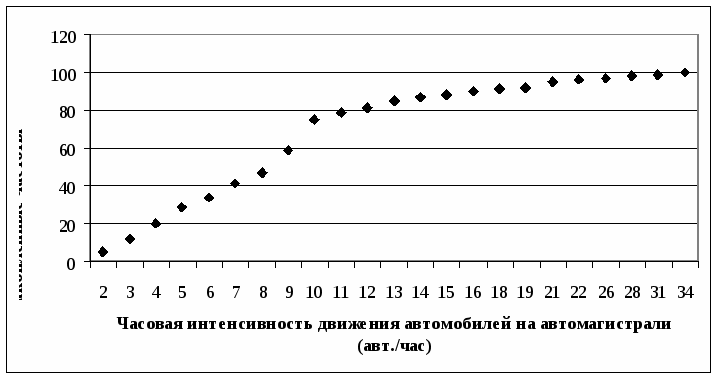 Огива. 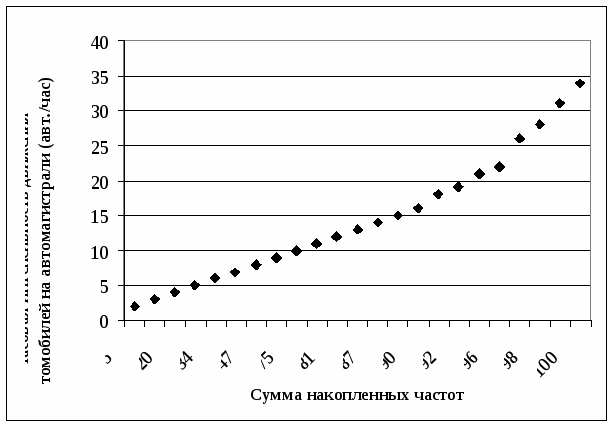 1.7. Дать анализ полученных результатов. Опираясь на полученные данные, рассчитанные в результате проведения статистического анализа часовой интенсивности движения автомобилей по автомагистрали, можно сделать следующий вывод. 1. Средняя интенсивность движения автомобилей по автомагистрали около 9 автомобилей в час (8,82 и 9,64 автомобиля). 2. В течение времени наблюдения мимо наблюдателя, за один час, чаще всего проезжало 10 автомобилей, так как мода равна 10 (7,8). 3. Часовая интенсивность движения достаточно сильно различается по автодорогам, так как коэффициент вариации и размах вариации достаточно большие (60,09% и 60,54%) и 29 соответственно) это позволяет сделать вывод о загруженности дорог. 4. Среднее квадратичное отклонение, которое является более точным показателем, говорит нам о том, что интенсивность движения на различных дорогах отличается от среднего значения интенсивности на 5 автомобилей, как в большую так и в меньшую сторону. 5. Различие показателей вариации, рассчитанных по дискретному и интервальному рядам характеризуется особенностями расчета этих показателей, но в большинстве случаев рассчитанные показатели не имеют значительного различия.
Раздел 2. Статистические группировки. 2.1. Имеются данные о показателях деятельности 30 дорожно – строительных организаций. Первоначальный ряд.
Ранжированный ряд.
2.2. С помощью аналитической группировки выявить характер взаимосвязи между результативным признаком «Прибыль строительной организации» и факторным признаком «Среднегодовая стоимость ОПФ». Для начала определим число интервалов по формуле Стержеса. n = 1 + 3,322∙lgN, где n – число интервалов, N – общее число единиц совокупности. n = 1 + 3, 322∙1,4771 = 5,91 Исходя из этого, будем рассматривать интервальный ряд с количеством интервалов 5.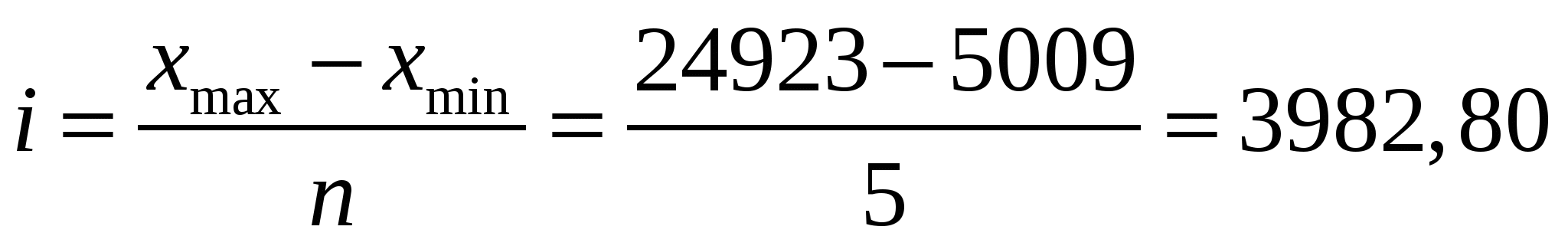  
2.3. Построить поле корреляции и эмпирическую линию регрессии. 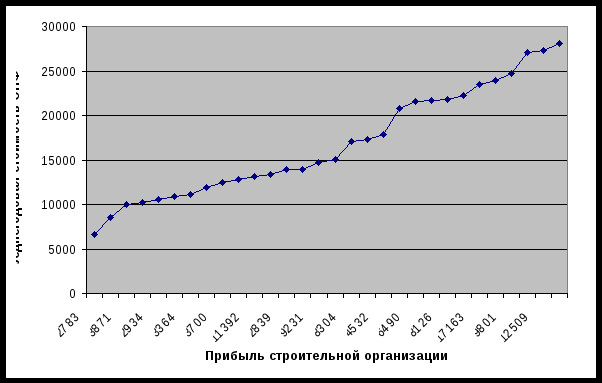 2 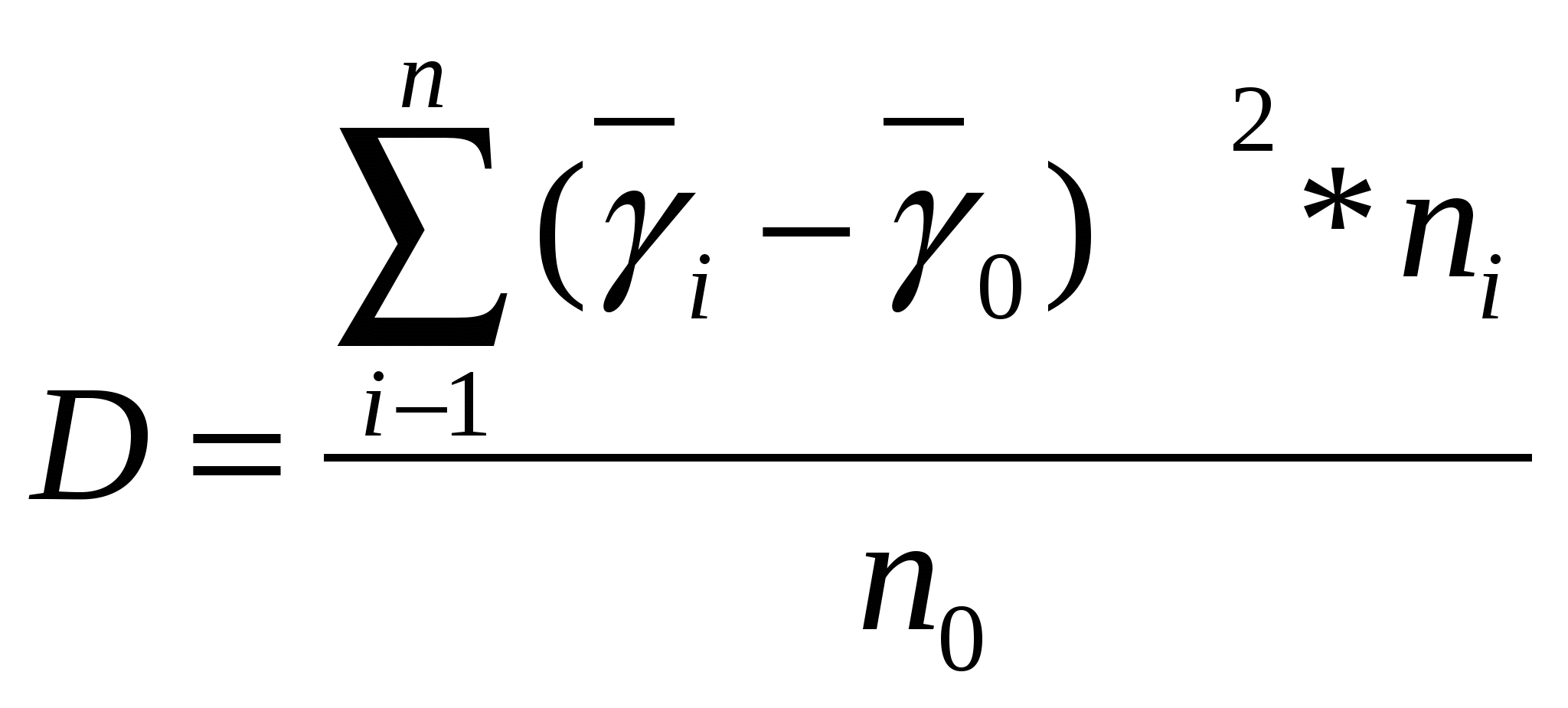 .4.Рассчитать величины межгрупповой, средней из внутригрупповых и общей дисперсий. |