РАСЧЕТ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ КОНСТРУЦИЙ вариант 13. Курсовая работа по статике расчет плоских и пространственных конструкций
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИИ ФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра теоретической механики КУРСОВАЯ РАБОТА ПО СТАТИКЕ «РАСЧЕТ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ КОНСТРУКЦИЙ» Выполнил: Руководитель: Ткач О.А. Тула, 2022 ОГЛАВЛЕНИЕ АННОТАЦИЯ 3 1 Расчет плоской шарнирной фермы 4 Определение реакции опор аналитическим способом. 4 2. Определение усилий в стержнях фермы методом вырезания узлов. 6 Аналитический метод определения сил реакций стержней. 6 Графический метод определения сил реакций в стержнях фермы. 10 Диаграмма Максвелла–Кремоны 12 Метод Риттера 14 3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ 16 3.1. Расчет конструкции № 1 16 3.2. Расчет конструкции № 2 18 3.3. Расчет конструкции № 3 21 3.4. Расчет конструкции № 4 23 4. РАСЧЕТ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ 26 СПИСОК ЛИТЕРАТУРЫ 29 АННОТАЦИЯИсследуется равновесие твердых тел и их систем на примере таких технически важных конструкций, как плоские шарнирные фермы, балки, валы, плиты и пластинки с использованием аналитических и графических методов. Для каждой расчетной схемы составлены уравнения равновесия и определены реакции внешних и внутренних связей разными методами. 1 Расчет плоской шарнирной фермыДано: Р1=10кН; Р4=15кН;a=1,2м,b=1,4м,α=900 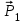 Рис.1.1 Определение реакции опор аналитическим способом.Освободимся от связей, заменяя их действие силами реакций. Опора А – неподвижный шарнир, направление реакции в которой заранее неизвестно. Выберем систему координат и разложим её на составляющие вдоль осей координат: 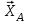 и и 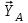 , направленные вдоль координатных осей. Стержневая опора В препятствует перемещению в направлении этого стержня, поэтому ее реакция , направленные вдоль координатных осей. Стержневая опора В препятствует перемещению в направлении этого стержня, поэтому ее реакция 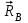 будет направлена вдоль линии стержня. будет направлена вдоль линии стержня. Таким образом, получили свободное тело, на которое действует система активных сил 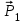 , , 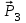 и сил реакций и сил реакций 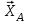 и и 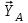 , , 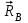 , которая находится в равновесии. Составим уравнения равновесия для заданной фермы: , которая находится в равновесии. Составим уравнения равновесия для заданной фермы: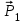 Рис.1.2 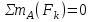 , , 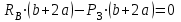 (1) (1)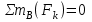 , , 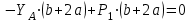 (2) (2)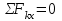 , , 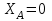 (3) (3)Из уравнения (1) получаем: 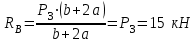 Из (2): 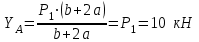 Окончательно получаем: 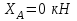 ; ; 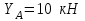 ; ; 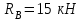 2. Определение усилий в стержнях фермы методом вырезания узлов.Так как стержни являются невесомыми, то силы реакций будут направлены вдоль этих стержней. Стержни и узлы пронумеруем так, как показано на рис. 1.3. Определим силы реакций стержней фермы аналитически. 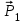 Рис.1.3 Аналитический метод определения сил реакций стержней.Выбираем узел, в котором сходятся не более двух стержней силы реакции в которых неизвестны. Такими узлами в нашей задаче являются узлы I , VII. Пусть стержни условно растянуты (силы реакции направлены внутрь стержня). Если сила реакции стержня будет отрицательной, то данный стержень находится в сжатом состоянии. Из геометрии фермы видно, что 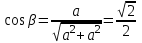 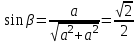 . . 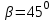 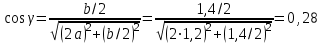 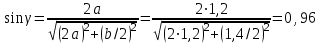 . . 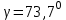 . .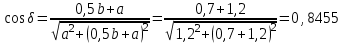 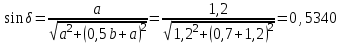 . . 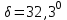 . .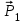 Рис.1.4 Составим уравнения равновесия для узлов I - IV: Узел I: 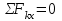 , , 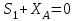 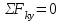 , , 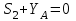 Из первого уравнения: 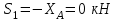 - стержень не нагружен - стержень не нагруженИз второго уравнения: 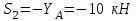 - стержень сжат - стержень сжатУзел II: 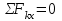 , , 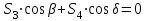 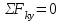 , , 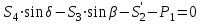 Уравнения можно записать в виде: 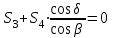 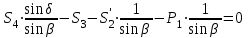 Откуда получаем, сложив уравнения: 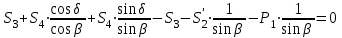 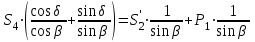 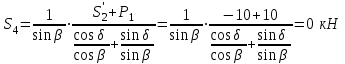 стержень не нагружен стержень не нагруженТогда 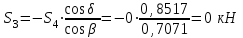 - стержень не нагружен - стержень не нагруженУзел III: 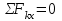 , , 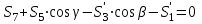 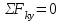 , , 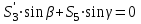 Из второго уравнения: 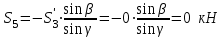 - стержень не нагружен - стержень не нагруженИз первого уравнения: 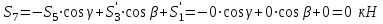 - стержень не нагружен - стержень не нагруженУзел IV: 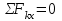 , , 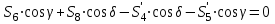 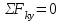 , , 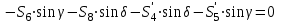 Уравнения можно записать в виде: 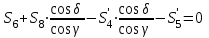 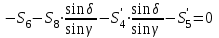 Откуда получаем, сложив уравнения: 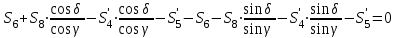 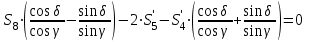 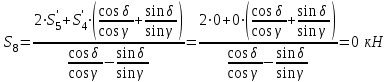 - стержень не нагружен - стержень не нагруженТогда 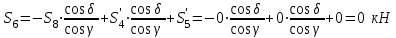 - стержень не нагружен - стержень не нагруженРассмотрим узлы V - VII (рис.1.5) Узел V: 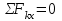 , , 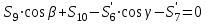 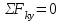 , , 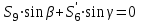 Из второго уравнения: 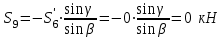 - стержень не нагружен - стержень не нагруженИз первого уравнения: 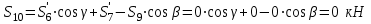 - стержень не нагружен - стержень не нагружен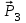 Рис.1.5 Узел VI: 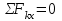 , , 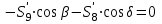 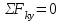 , , 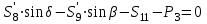 Из второго уравнения: 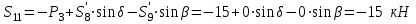 - стержень сжат. - стержень сжат.Подставив вычисленные ранее значения в первое уравнение, проверим правильность проведенных вычислений 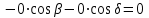 Узел VII так же используем для проверки правильности вычислений: 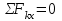 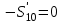 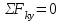 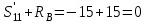 Следовательно, расчеты проведены верно. Сведем полученные данные в таблицу:
Графический метод определения сил реакций в стержнях фермы.Силы реакций определяются из условия замкнутости силового многоугольника при равновесии для каждого из узлов фермы. Построение силового многоугольника начнем с узла I, учитывая, что направление усилий в стержнях должно совпадать с направлением стержней фермы. Изобразим в масштабе 1 см – 2 кН силу 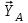 . Из начала . Из начала 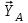 проведем прямую, параллельную линии действия реакции проведем прямую, параллельную линии действия реакции 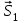 , а из конца , а из конца 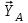 – силу – силу 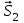 . .Точка пересечения этих прямых будет неизвестной вершиной силового многоугольника. Определяем направления реакций стержней и измеряя длину полученных векторов с учетом масштаба находим искомые усилия. Узлы перебираем в том порядке, в котором проводили расчет реакций аналитическим методом. Силовой многоугольник последнего узла (узла VII) строим по найденным усилиям, чтобы убедится, что он замкнут и расчеты проведены верно. Измерив полученные отрезки на плане сил с учётом выбранного масштаба, определим величины и направления неизвестных реакций, которые сведем в таблицу:
Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений 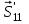 Рис.1.6 Диаграмма Максвелла–КремоныСтроим ферму в масштабе. Изображаем все силы, действующие на ферму. Обозначаем внешние поля — области чертежа, разделенные силами и стержнями фермы — А,В,С, D, E (рис. 1.7) Обозначаем внутренние поля F, G, H, I,J . Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям. Приведем таблицу соответствия имен.
Строим многоугольник внешних сил. Выберем направление обхода фермы по часовой стрелке. Начинаем с произвольной силы, например, Р1. Откладывая в масштабе (1cм-2кН) эту силу и соблюдая ее направление, обозначаем начальную и конечную точку строчными буквами a и b, соответствующими направлению обхода — из поля A в поле B. Следующая по часовой стрелке нагрузка — P3. Строим ее в точке b вслед за силой Р1. Конечную точку помечаем буквой c. Обход фермы продолжаем, пока многоугольник не замкнется. Последней будет сила реакция опоры XA, обозначенная как EA. Конец ее попадает на исходную точку. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены два соседних с ним поля. Таким образом, начинать графический расчет можно с поля F, у которого соседние поля A и D определены на диаграмме. По направлению стержней AF и DF проводим линии через точки a и d диаграммы. Точка их пересечения - f. Длины afи df равны абсолютным значениям усилий в соответствующих стержнях. Аналогично рассматриваем остальные поля. Окончательные результаты заносим в таблицу:
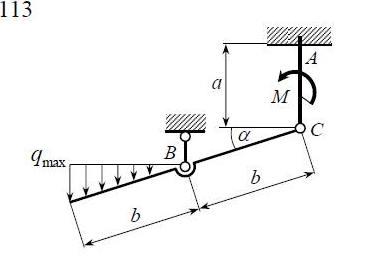
Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений и масштаба построения диаграммы 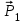 Рис.1.7 Метод РиттераОпределим усилия в стержнях 1,3,4. Для определения нужного усилия по методу Риттера рассечем ферму по стержням 1,3,4 на части прямой I-I и рассмотрим равновесие левой части (рис.1.8). Действие отброшенной части заменим действием сил реакций. 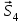 Рис.1.8 Для этого будем считать, что стержни в рассматриваемом сечении условно растянуты (силы реакций S1, S3, S4направлены внутрь стержней). Составим уравнения равновесия для полученной части фермы: Уравнение моментов относительно узла III: 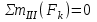 , , 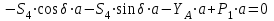 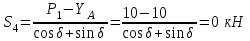 Уравнение моментов относительно узла II: 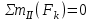 , , 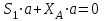 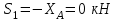 Уравнение проекций сил на ось Y: 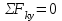 , , 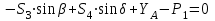 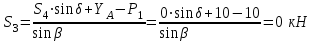 Определим усилия в стержнях 7,6,8. Для определения нужного усилия по методу Риттера рассечем ферму по стержням 7,6,8 на части прямой II-II и рассмотрим равновесие правой части (рис.1.9). Действие отброшенной части заменим действием сил реакций. 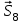 Рис.1.9 Составим уравнения равновесия для полученной части фермы: Уравнение моментов относительно узла V: 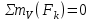 , , 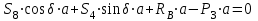 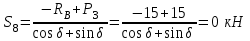 Уравнение моментов относительно узла IV: 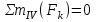 , , 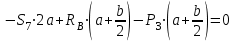 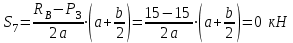 Уравнение проекций сил на ось Y: 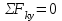 , , 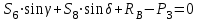 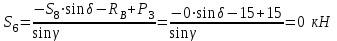 Полученные результаты совпадают с предыдущими расчетами 3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ3.1. Расчет конструкции № 1113
Решение. 1. Рассмотрим равновесие части ВС. 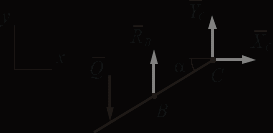 Заменяем распределенную нагрузку сосредоточенной силой 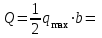 5 кН. 5 кН.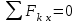 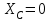 (1) (1)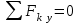 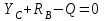 (2) (2)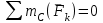 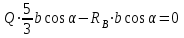 (3) (3)2. Рассмотрим равновесие части АС. 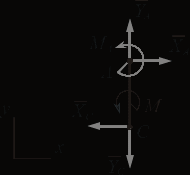 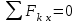 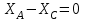 (4) (4)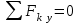 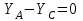 (5) (5)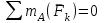 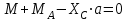 (6) (6)Подставляя исходные данные в уравнения равновесия (1 – 6) получим: Из (1) 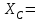 0 кН; 0 кН;(3) 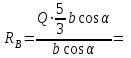 8,33 кН; 8,33 кН;(2) 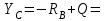 -3,33 кН; -3,33 кН;(4) 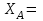 0 кН; 0 кН;(5) 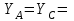 -3,33 кН; -3,33 кН;(6) 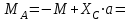 -6,2 кН. -6,2 кН.Знак «–» при определении реакций говорит о том, что истинное направление данной реакции противоположное. 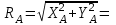 3,33 кН, 3,33 кН, 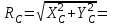 3,33 кН. 3,33 кН.Ответ: 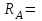 3,33 кН; 3,33 кН; 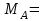 -6,2 кНм; -6,2 кНм; 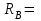 8,33 кН; 8,33 кН; 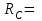 3,33 кН. 3,33 кН.3.2. Расчет конструкции № 2213
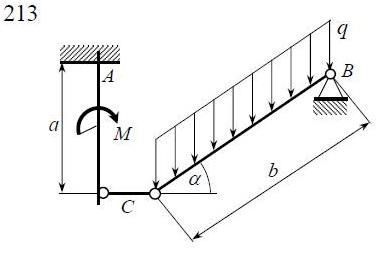
Решение. 1. Рассмотрим равновесие части ВС. 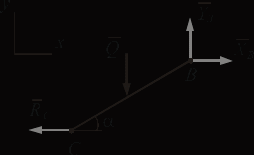 Заменяем распределенную нагрузку сосредоточенной силой 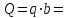 6 кН. 6 кН.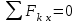 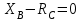 (1) (1)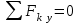 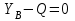 (2) (2)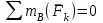 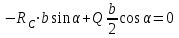 (3) (3)2. Рассмотрим равновесие части АС. 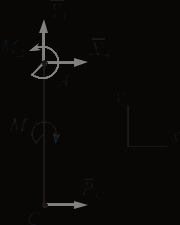 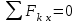 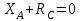 (4) (4)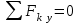 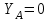 (5) (5)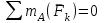 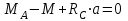 (6) (6)Подставляя исходные данные в уравнения равновесия (1 – 6) получим: Из (2) 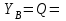 6 кН; 6 кН;(3) 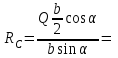 3 кН; 3 кН;(1) 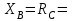 3 кН; 3 кН;(4) 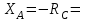 -3 кН; -3 кН;(5) 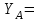 0 кН; 0 кН;(6) 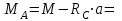 3,8 кН. 3,8 кН.Знак «–» при определении реакций говорит о том, что истинное направление данной реакции противоположное. 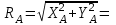 3 кН, 3 кН, 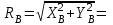 6,71 кН. 6,71 кН.Ответ: 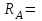 3 кН; 3 кН; 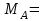 3,8 кНм; 3,8 кНм; 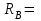 6,71 кН; 6,71 кН; 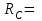 3 кН. 3 кН.3.3. Расчет конструкции № 3313
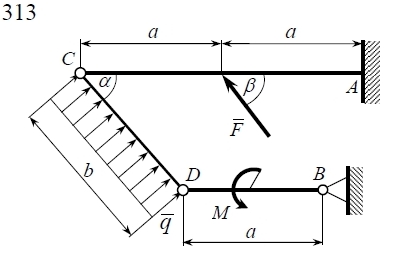
Решение. 1. Рассмотрим равновесие части BD.  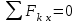 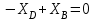 (1) (1)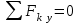 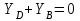 (2) (2)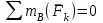 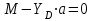 (3) (3)2. Рассмотрим равновесие части CD. 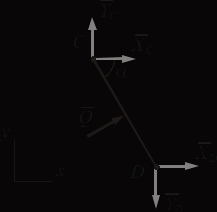 Заменяем распределенную нагрузку сосредоточенной силой 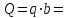 6 кН. 6 кН.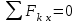 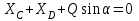 (4) (4)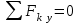 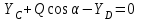 (5) (5)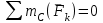 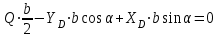 (6) (6)3. Рассмотрим равновесие части AC.  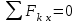 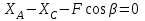 (7) (7)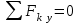  (8) (8)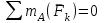 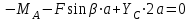 (9) (9)Подставляя исходные данные в уравнения равновесия (1 – 9) получим: Из (3) 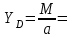 7,75 кН; 7,75 кН;(2) 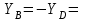 -7,75 кН; -7,75 кН;(6) 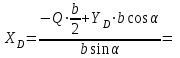 3,53 кН; 3,53 кН;(1) 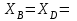 3,53 кН; 3,53 кН;(5) 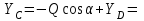 3,49 кН; 3,49 кН;(4) 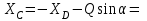 -7,79 кН; -7,79 кН;(7) 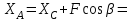 -16,49 кН; -16,49 кН;(8) 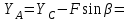 -1,51 кН; -1,51 кН;(9) 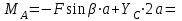 1,58 кНм. 1,58 кНм.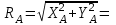 16,56 кН, 16,56 кН, 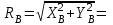 8,52 кН, 8,52 кН,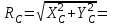 8,54 кН, 8,54 кН, 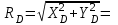 8,52 кН. 8,52 кН.Ответ: 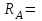 16,56 кН, 16,56 кН, 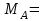 1,58 кНм, 1,58 кНм, 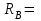 8,52 кН, 8,52 кН, 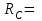 8,54 кН, 8,54 кН, 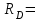 8,52 кН. 8,52 кН.3.4. Расчет конструкции № 4413
Решение. 1. Рассмотрим равновесие конструкции в целом 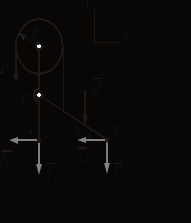 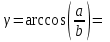 36,9o. 36,9o.Заменяем распределенную нагрузку сосредоточенной силой 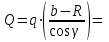 1,5 кН. 1,5 кН.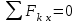 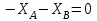 (1) (1)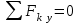 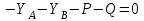 (2) (2)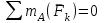 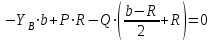 (3) (3)2. Рассмотрим равновесие части ВС. 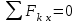 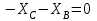 (4) (4)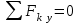 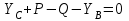 (5) (5)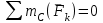 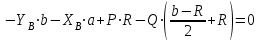 (6) (6)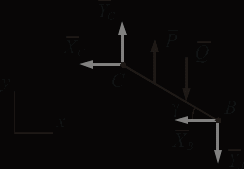 Подставляя исходные данные в уравнения равновесия (1 – 6) получим: Из (3) 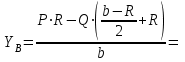 12,25 кН; 12,25 кН;(2) 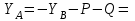 -30,75 кН; -30,75 кН;(5) 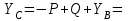 -3,25 кН; -3,25 кН;(6) 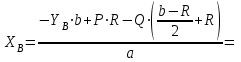 0; 0;(1) 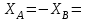 0; 0;(4) 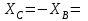 0. 0.Знак «–» при определении реакций говорит о том, что истинное направление данной реакции противоположное. 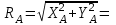 30,75 кН, 30,75 кН, 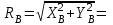 12,25 кН, 12,25 кН, 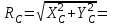 3,25 кН. 3,25 кН.Ответ: 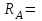 30,75 кН, 30,75 кН, 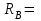 12,25 кН, 12,25 кН, 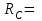 3,25 кН. 3,25 кН.4. РАСЧЕТ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИП13
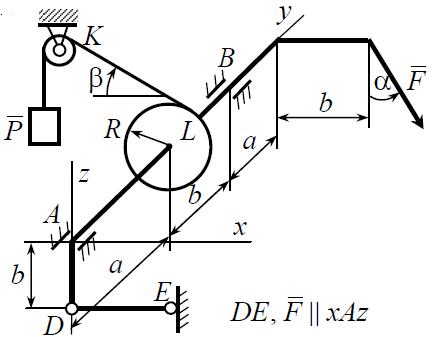
Решение. 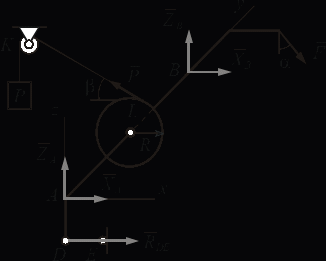 Составим уравнения равновесия 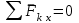 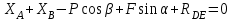 (1) (1)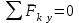 ––– (2) ––– (2)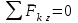 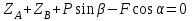 (3) (3)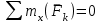 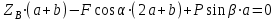 (4) (4)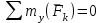 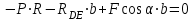 (5) (5)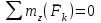 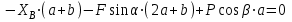 (6) (6)Подставляя исходные данные в уравнения равновесия (1 – 6) получим: Из (5) 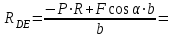 -7,9 кН; -7,9 кН;(6) 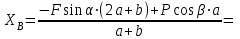 -4,87 кН; -4,87 кН;(1) 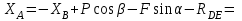 18,72 кН; 18,72 кН;(4) 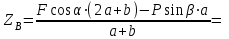 6,95 кН; 6,95 кН;(3) 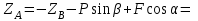 -7,35 кН. -7,35 кН.Знак «–» при определении реакций говорит о том, что истинное направление данной реакции противоположное. 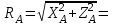 20,11 кН; 20,11 кН; 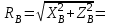 8,49 кН. 8,49 кН.Ответ: 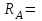 20,11 кН; 20,11 кН; 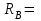 8,49 кН, 8,49 кН, 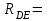 -7,9 кН. -7,9 кН.ВЫВОДЫ В результате выполнения курсовой работы получены навыки исследования равновесия твердых тел и их систем. В курсовой работе выполнен расчет плоской шарнирной фермы. Для нахождения усилий в стержнях использовались аналитические методы (вырезания узлов и Риттера) и графические методы (вырезания узлов, построение диаграммы Максвелла-Кремоны), для нахождения реакций опор кроме аналитического метода сечений рассмотрены графические методы (построение силового и веревочного многоугольников). Результаты расчетов различными методами сходятся вплоть до ошибок измерения и округления . СПИСОК ЛИТЕРАТУРЫ1. Бертяев В.Д., Латышев И.И., Маркелов С.С. Расчет плоских и пространственных конструкций: Учеб. пособие. – Тула: ТулГУ, 2011. – 79 с. 2. Бертяев В.Д. Теоретическая механика на базе Mathcad. Практикум. – СПб.: БХВ-Петербург, 2005. – 752 с. 3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т.1. – М.: Наука, 1979. – 272 с. 4. Тарг С.М. Краткий курс теоретической механики. – М.: Высш. шк., 2005. – 416 с. 5. Яблонский А.А., Никифорова В.М. Курс теоретической механики: Статика. Кинематика. Динамика. – М.: Интеграл-Пресс, 2006. – 608 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

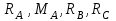 .
.
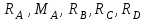 .
.
 .
.
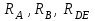 .
.