эссе. Новый документ (26). Курсовая работа решение систем дифференциальных уравнений методом преобразования Лапласа Выполнил студент Иванов Иван Иванович
 Скачать 39.12 Kb. Скачать 39.12 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Псковский государственный университет» Институт математического моделирования и игропрактики Кафедра математики и теории игр КУРСОВАЯ РАБОТА Решение систем дифференциальных уравнений методом преобразования Лапласа Выполнил студент Иванов Иван Иванович Код, направление подготовки 44.03.01 Педагогическое образование Профиль Математика Научный руководитель: Сергеев С.С., доцент кафедры математики и теории игр, кандидат физико-математических наук, доцент Оценка:_______________ Подпись научного руководителя ______________ Псков 2021 ВВЕДЕНИЕ Актуальность исследования. Тригонометрия – существенная и значимая составляющая школьного курса алгебры; данный материал традиционно применяется в математических олимпиадах, играя роль своего рода инструмента отбора. В средней школе продолжительный период существовал отдельный курс тригонометрии, с достаточным количеством учебников и задачников. Однако в современных учебных материалах четко прослеживается тенденция переносить темы тригонометрии и тождественных преобразований тригонометрических выражений в курс старших классов, а, следовательно, можно сказать, что со временем тригонометрический материал «растворился» в направлениях геометрии, алгебры, математического анализа. Однако, несмотря на все вышесказанное тема «Тождественные преобразования тригонометрических выражений» играет значимую роль. Очень часто для решения тригонометрических уравнений и неравенств, а так же для комбинированных заданий и решения задач на упрощение тригонометрических выражений требуется широкая база знаний о правилах преобразования алгебраических выражений и тригонометрических формул (уметь применять их как по одной, так и в комплексе). В соответствии с этим, сохраняется необходимость в эффективной организации обучения данному блоку содержания. Объект исследования: процесс обучения математике в основной школе. Предмет исследования: обучение тождественным преобразованиям тригонометрических выражений в основной школе. Цель работы: проработать выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а так же комбинированных заданий. Для решения задач на упрощение тригонометрических выражений требуется достаточно хорошо знать правила преобразования алгебраических выражений и тригонометрические формулы (уметь применять их как по одной, так и в комплексе). 1.1. Понятие и содержание линии тождественных преобразований в курсе алгебры основной школы. Линия тождественных преобразований является одной из четырех основных разделов содержательных линий школьного курса алгебры (учение о функции, числе, уравнения и неравенства, тождественные преобразования). Она изучается в течение всего курса математики, начиная с начальных классов. В первом параграфе будут рассмотрены основные понятия данной содержательной линии такие как: «выражение», «тождественно равные выражения», «тождество» и «тождественные преобразования выражений». Выражением в математике называют запись, состоящую из чисел, букв (обозначающих постоянные или переменные величины), знаков математических действий. В числовых множествах имеют дело с числовыми выражениями. Школьный курс математики выделяет два основных класса математических выражений: алгебраические и неалгебраические (трансцендентные).Алгебраическим выражением называется выражение, составленные из конечного числа букв и цифр, соединенных знаками действий (сложение, вычитание, умножение, деление, возведение в целую степень и извлечения корня). Трансцендентными называются аналитические функции, которые не являются алгебраическими (тригонометрические, логарифмические и показательные). Тождество – это равенство, верное при любых допустимых значениях входящих в его состав переменных. Например: 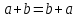 , , 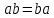 . . В дальнейшем вводится сначала определение тождественно равных выражений : Два выражения, соответственные значения которых равны при любых значениях переменных, называются тождественно равными. После этого дается понятие тождественного преобразования выражений: Тождественное преобразование выражения – это замена исходного выражения на выражение, тождественно равное ему. В этом определении слово «тождественное» иногда опускают, и говорят просто «преобразование выражения», при этом понимают, что речь идет о тождественном преобразовании. В своей работе я подробно рассмотрю тождественные преобразования тригонометрических выражений. Преобразование тригонометрических выражений опирается на определение тригонометрических функций, формулы приведения, основные тригонометрические тождества и др. Они применяются при нахождении значений в упрощении выражений, в доказательстве тождеств и в других случаях. Начать знакомство с преобразованиями следует с определения тригонометрического выражения. Тригонометрическим выражением называется выражение, которое содержит переменные под знаком тригонометрических функций. Например, выражения 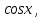 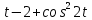 являются тригонометрическими. Выражения являются тригонометрическими. Выражения 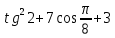 , , 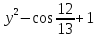 , тригонометрическими не являются: первое из них не содержит переменных, второе, хотя и содержит переменную , тригонометрическими не являются: первое из них не содержит переменных, второе, хотя и содержит переменную 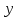 , но не под знаком тригонометрической функции. Замена тригонометрического выражения другим, тождественно равным ему на некотором множестве, называется тождественным преобразованием данного выражения на этом множестве. , но не под знаком тригонометрической функции. Замена тригонометрического выражения другим, тождественно равным ему на некотором множестве, называется тождественным преобразованием данного выражения на этом множестве.Все задания на преобразование тригонометрических выражений можно условно разделить на 3 вида: 1)найти значение выражения; 2)вычислить при заданных условиях; 3)найти наибольшее или наименьшее значение функции. В тождественных преобразованиях тригонометрических выражений могут быть использованы следующие алгебраические приемы: добавление и вычитание одинаковых слагаемых; вынесение общего множителя за скобки; умножение и деление на одну и ту же величину; применение формул сокращенного умножения; выделение полного квадрата; разложение квадратного трехчлена на множители; введение новых переменных с целью упрощения преобразований. При преобразованиях тригонометрических выражений, содержащих дроби, Тождественные преобразования тригонометрических выражений можно использовать свойства пропорции, сокращение дробей или приведение дробей к общему знаменателю. Кроме того, можно пользоваться выделением целой части дроби, умножением числителя и знаменателя дроби на одинаковую величину, а также по возможности учитывать однородность числителя или знаменателя. При необходимости можно представлять дробь в виде суммы или разности нескольких более простых дробей. Кроме того, применяя все необходимые методы преобразования тригонометрических выражений, необходимо постоянно учитывать область допустимых значений преобразуемых выражений. Для преобразования тригонометрических выражений используют свойства тригонометрических функций, и формулы тригонометрии. Тождественные преобразования тригонометрических выражений опираются на следующие основные формулы: основные тригонометрические тождества : 1) 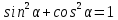 2) 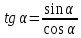 3) 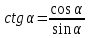 4) 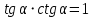 5) 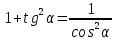 6) 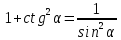 формулы приведения: Под формулами приведения понимают обычно формулы, сводящие значение тригонометрической функции аргумента вида 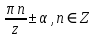 , к функции аргумента , к функции аргумента 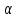 . Пусть, например, нужно вычислить . Пусть, например, нужно вычислить 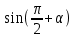 . .Имеем: 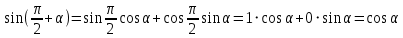 . .Аналогично, 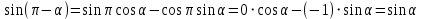 ; ;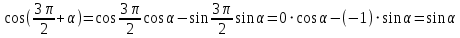 Подобным же образом выводятся и остальные формулы приведения. Эти формулы представлены в следующей таблице: 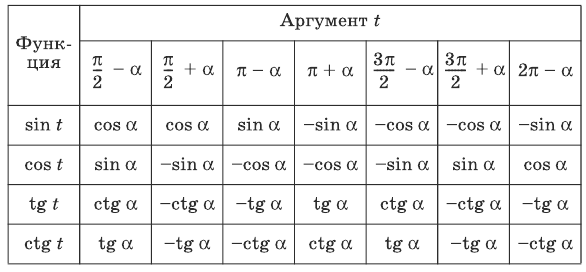 формулы суммы и разности аргументов 1) 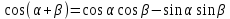 2) 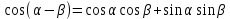 3) 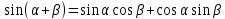 4) 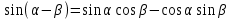 5) 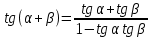 6) 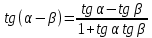 формулы двойного аргумента: 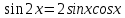 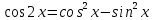 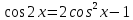 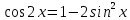 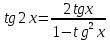 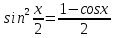 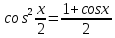 формулы половинного аргумента 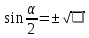 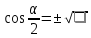 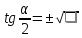 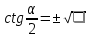 формулы преобразования суммы (разности) тригонометрических функций в произведение 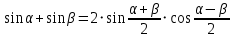 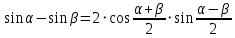 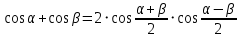 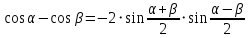 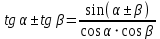  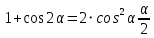  формулы преобразования произведения тригонометрических функций в сумму (разность) 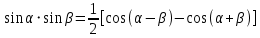 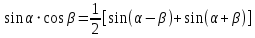 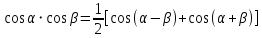 Характерная особенность преобразования тригонометрических выражений состоит в том, что к одному и тому же результату можно прийти разными путями. Таким образом, в первом параграфе были рассмотрены основные понятия содержательной линии тождественных преобразований, такие как: “выражение”, “тождественно равные выражения”, “тождество”, “тождественные преобразования выражений”, “алгебраическое выражение” и “неалгебраическое выражение”, “тригонометрическое выражение”. Были приведены примеры тригонометрических выражений, описаны необходимые свойства и формулы тригонометрических функций и тригонометрии для преобразования тождеств. 2. Виды тригонометрических выражений. В школьном курсе алгебры и начал анализа рассматриваются два вида тригонометрических выражений: числовые и буквенные. Тригонометрическое выражение, в котором используются только тригонометрические функции, числа, знаки арифметических действий и скобки, называется числовым выражением. Если в записи выражения используются не только числа, но и буквы, то выражение называется буквенным. В записи буквенных выражений используют буквы латинского алфавита. Приведем примеры числовых тригонометрических выражений: 1)Найдите значение выражения 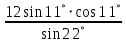 , ,Решение. Используем формулу синуса двойного угла 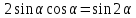 : :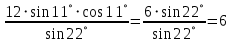 2)Найдите значение выражения 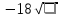 Решение. Выполним преобразования: 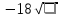 3)Найдите значение выражения 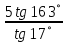 , ,Решение. Выполним преобразования: 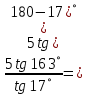 При выполнении преобразований наиболее распространенной ошибкой у учащихся является попытка сократить стоящие в числителе и знаменателе одинаковые выражения, одно из которых (или в числителе, или в знаменателе), а порой и оба, являются не сомножителями, а слагаемыми. Рассмотрим типовые примеры, связанные с тождественными преобразованиями буквенных тригонометрических выражений: 1)Найдите значение выражения 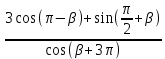 . .Решение. В силу периодичности косинуса 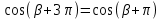 . Далее используем формулы приведения: . Далее используем формулы приведения: 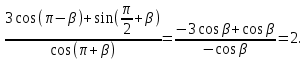 2)Найдите 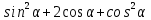 , если , если 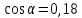 . .Решение. Согласно основному тригонометрическому тождеству 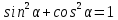 , откуда , откуда 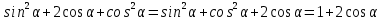 , что при , что при 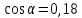 равно равно 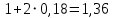 . .3)Найдите 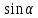 , если , если 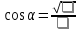 и и 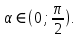 Решение. Так как 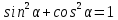 , то , то 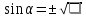 Так как 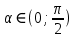 , то , то 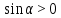 , следовательно, , следовательно, 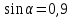 . . |
