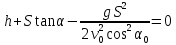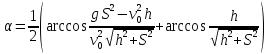|
|
Развитие у обучающихся интереса к физике с использованием физических экспериментальных задач. Курсач. Курсовая работа студент группы фи1601 Глухов Иван Научный Зуев Петр Владимирович
Экспериментальные задачи могут быть использованы в любой части урока. Такая задача может стать темой данного урока. В этом случае необходимо, чтобы вопрос вызывал некоторое удивление, и желание решить его. Таким средством стимула к восприятию является постановка проблемы, а значит, нужна подходящая экспериментальная задача. Применять задачу можно для проверки степени понимания учениками изучаемого на уроке материала, для его закрепления. Задача в этом случае способствует углублению и уточнению нового материала. Использование экспериментальных задач при опросе даёт нам возможность выяснить, насколько правильно и глубоко усвоен пройденный материал. Экспериментальные задачи могут быть предложены учащимся в качестве домашнего задания. Задания должны быть такими, чтобы для домашних опытов ученики нашли нужные приборы и предметы. Сложные экспериментальные задачи можно выполнять на факультативных занятиях. Занимательные экспериментальные задачи можно использовать на физических вечерах.
Проверка правильности решения таких задач может быть осуществлена разными способами в зависимости от содержания задач. Решение большинства количественных задач проверяется путём непосредственного измерения искомой величины с помощью соответствующих приборов; с помощью другого контрольного опыта, т. е. другим способом и другими приборами; по паспортным данным или таблицам. Решение качественных задач проверяется, как правило, с помощью постановки контрольного опыта. Например, в задаче дано описание опыта, требуется предсказать его результаты. Контрольный эксперимент, выполненный учеником, либо подтвердит его ответ, либо опровергнет. Частичного совпадения логического решения и опыта здесь не должно быть, поэтому необходимо свести к минимуму все побочные факторы, отрицательно влияющие на результат эксперимента. Приборы для контрольного опыта заранее выдавать не следует. Иначе, как правило, ученик сначала проделывает контрольный опыт, а потом подгоняет решение к результату эксперимента.
Основные этапы решения экспериментальной задачи сходны с решением любой физической задачи, но также имеются свои особенности. Характерным для решения таких задач является поиск нужных для решения данных, а также способов получения этих данных. Поэтому при анализе задачи и составлении плана решения важным моментом является поиск ответов на вопросы: какие данные необходимы для решения? Как их получить, используя опыт? В каких единицах они должны быть выражены? Поскольку эта работа обучающихся носит творческий характер, то этот этап обучение должен быть разработан более тщательно. Учитель, готовя экспериментальную задачу, должен предварительно опробовать необходимое оборудование.
Такие задачи могут быть использованы в любой части урока, но цели применения, методика и содержание задач будут несколько различны.
Содержание экспериментальной задачи является темой данного урока. В ходе ее решения происходит усвоение новых понятий, закономерностей и зависимостей. Например, закон Ома для участка цепи можно объяснить, решая две такие задачи: «Проверить, зависит ли (и если да, то как) сила тока в данной спирали от напряжения на ее клеммах?» Проверить, зависит ли (и если да, то как) сила тока в данной цепи от изменения сопротивления магазина, включенного в эту цепь, при постоянном напряжении на его клеммах?» [18].
В этом случае нужно, чтобы постановка вопроса вызвала у обучающихся желание познать новые закономерности. Одним из средств создания стимула к восприятию нового материала является постановка проблемы, в качестве которой может быть подобрана подходящая экспериментальная задача. Условие задачи должно удовлетворять требованиям:
Все приборы, которые применяются в задаче, должны быть знакомы ученикам, все сопутствующие явления понятны.
Содержание задачи не должно подсказывать решение проблемы, которую ученики разрешат в ходе урока.
Постановка вопроса должна возбудить желание решить его.
Использование задач в качестве иллюстраций, подтверждающих правильность и важность сделанных теоретических выводов. Например, после выяснения вопроса о связи скорости движения молекул с температурой тела можно решить такую задачу: «В стаканы с холодной и горячей водой бросили одинаковые кусочки марганцовки. В каком из них вода окрасится быстрее по всему объему?». В результате решения этой задачи ученики убеждаются в правильности сделанного теоретического вывода [24].
Применение задач для проверки степени понимая изученного на уроке материала и для его закрепления. В данном случае решение задач способствует углублению и уточнению нового материала.
Использование экспериментальных задач при опросе дает возможность выяснить, насколько правильно, глубоко и сознательно ученик усвоил ранее пройденный материал. Вызванному ученику дается карточка с текстом задачи и все необходимые приборы. Иногда полезно (если позволяет время) выдавать ученику не все приборы, нужные для решения задачи, или давать их больше, чем требует решение или предоставлять право выбора всех приборов, необходимых для проведения эксперимента [21].
Весьма полезны 20-ти минутные классные упражнения учащихся по решению экспериментальных задач с последующим разбором и выяснением причин допущенных ошибок.
Несколько раз в учебном году можно проводить контрольные работы по решению экспериментальных задач.
Особый интерес у учеников вызывает решение экспериментальных задач в качестве задания на дом. Они могут быть как индивидуальными, так и одинаковыми для всех. Учитель должен быть уверен, что нужные приборы и предметы ученики найдут дома.
Наиболее сложные экспериментальные задачи можно использовать на факультативных занятиях и в работе физического кружка.
2. Решение экспериментальных задач в курсе механики
Важнейшим элементом обучения является использование на практике тех приборов и методов измерений, которые школьники уже изучили.
Физические эксперименты делятся на две большие группы: демонстрационные, которые, как правило, выполняются учителем, и практические работы, которые школьники выполняют самостоятельно.
Задача 1. Определить массу шарика.
Оборудование: два стальных шарика (один из них известной массы), пластилин, штатив, транспортир, две нити равной длины.
Решение. Прикрепим шарик известной массы 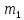 к нити длиной к нити длиной 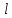 , отведем его на измеряемый транспортиром угол , отведем его на измеряемый транспортиром угол 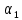 и отпустим. и отпустим.
В нижней точке траектории движения шарика массой 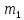 подвесим шарик неизвестной массы подвесим шарик неизвестной массы 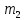 , к которому прикрепим кусочек пластилина массой Δm. , к которому прикрепим кусочек пластилина массой Δm.
П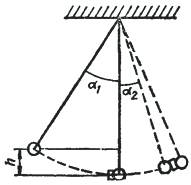 ри своем движении шарик массой ри своем движении шарик массой 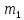 сталкивается с шариком массой сталкивается с шариком массой 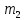 . Из-за наличия пластилина удар шариков является неупругим, после столкновения они отклоняются на некоторый, тоже измеряемый угол . Из-за наличия пластилина удар шариков является неупругим, после столкновения они отклоняются на некоторый, тоже измеряемый угол 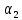 .При этом выполняется закон сохранения импульса: .При этом выполняется закон сохранения импульса:
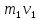 =( =(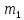 + +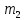 + +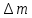 ) )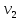 . .
Скорость 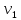 шарика известной массы в момент соударения находим из закона сохранения механической энергии шарика известной массы в момент соударения находим из закона сохранения механической энергии
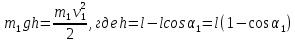
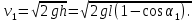
Поскольку масса кусочка пластилина Δm ничтожна мала, в дальнейшем ею будем пренебрегать.
Аналогично определим скорость 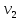 ; ;
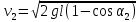 . .
Тогда из закона сохранения импульса получим:
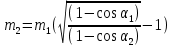 . .
И окончательно имеем:
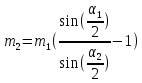 [16]. [16].
Задача 2. Определить максимальную скорость движения пальца руки.
Оборудование: камешек, линейка.
Решение. Положив камешек на край стола, щелкнем по нему пальцем и заметим точку падения камешка на пол. Измерим максимальное расстояние l от стола до места падения камешка, полученное в результате нескольких опытов. Тогда максимальная скорость пальца v(скорость, сообщенная в данном опыте камешку) вычислим по формуле:
v = 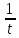 , (1) , (1)
где t (время полета камешка) можно определить по формуле
t =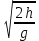 . (2) . (2)
Здесь h − высота стола, а g − ускорение свободного падения.
Подставляя t из формулы (2) в формулу (1), получим:
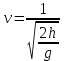 [16]. [16].
Задача 3. Определите плотность деревянного бруска.
Оборудование: линейка, сосуд с водой, мерный стакан.
Решение. Заполним сосуд (рекомендуется взять пластиковую тарелку) водой насколько это возможно. Пусть объем жидкости равен 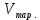 Аккуратно опустим брусок в пластиковую тарелку с водой. Объем вытесненной воды Аккуратно опустим брусок в пластиковую тарелку с водой. Объем вытесненной воды 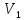 определим с помощью мерного стакана. Аккуратно погрузим весь брусок в воду. Некоторая часть воды вновь выльется из тарелки. Ясно, что всего из тарелки будет вытеснен объем воды равный объему бруска определим с помощью мерного стакана. Аккуратно погрузим весь брусок в воду. Некоторая часть воды вновь выльется из тарелки. Ясно, что всего из тарелки будет вытеснен объем воды равный объему бруска 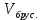 . . 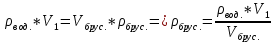 Несмотря на идейную простоту, задача требует известного экспериментального искусства и внимательности: объем воды умещающийся в тарелке оказывается больше объема тарелки, т. к. заметная часть воды "возвышается" над краем тарелки за счет сил поверхностного натяжения. Небрежно выполненный эксперимент приводит к ощутимой ошибке в определении плотности дерева [17]. Несмотря на идейную простоту, задача требует известного экспериментального искусства и внимательности: объем воды умещающийся в тарелке оказывается больше объема тарелки, т. к. заметная часть воды "возвышается" над краем тарелки за счет сил поверхностного натяжения. Небрежно выполненный эксперимент приводит к ощутимой ошибке в определении плотности дерева [17].
Задача 4. Определите плотность металла, находящегося в одном из двух кусков пластилина, если известно, что массы пластилина в обоих кусках одинаковы. Оцените точность полученного результата. Извлекать металл из пластилина не разрешается.
Оборудование: весы с разновесами, стакан с водой, штатив, два одинаковых по массе куска пластилина, небольшой кусок металла или моток проволоки, введенный внутрь одного из кусков пластилина.
Решение. Задача очень похожа на знаменитую задачу о короне царя Гиерона (определение наличия примесей в золоте), только с более доступными материалами - пластилином и железом (кусок железа находился внутри пластилина).
Пользуясь весами с разновесами, можно определить массу куска пластилина с металлом (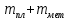 ), массу чистого пластилина ), массу чистого пластилина 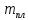 и по их разности - массу металла и по их разности - массу металла 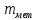 , находящегося в одном из кусков пластилина. Взвесив данные куски пластилина сначала в воздухе, а потом в воде, можно найти выталкивающую силу и, зная плотность воды, можно вычислить объемы кусков ( , находящегося в одном из кусков пластилина. Взвесив данные куски пластилина сначала в воздухе, а потом в воде, можно найти выталкивающую силу и, зная плотность воды, можно вычислить объемы кусков (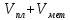 ) и ) и 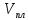 . Объем металла . Объем металла 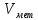 можно определить по разности этих объемов. можно определить по разности этих объемов.
Тогда плотность металла 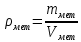 . .
Возможны два варианта: в одних кусках пластилина находился кусок алюминия, в других - кусок железа.
Весьма интересным было бы решение этой задачи, если бы вместо определенного куска чистого пластилина массой, равной массе пластилина в составном куске, давался просто пластилин (в неопределенном количестве). В этом случае для решения задачи надо было бы взять кусок чистого пластилина, масса которого равна массе (m) составного куска (объема V), и определить его объем 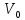 . Плотность металла можно найти, решив следующую систему четырех уравнений с четырьмя неизвестными: . Плотность металла можно найти, решив следующую систему четырех уравнений с четырьмя неизвестными:
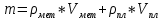
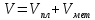
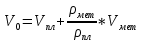
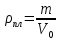 [17]. [17].
Задача 5. Оцените механическую работу, которую необходимо совершить для того, чтобы равномерно поднять плавающий в сосуде карандаш до уровня касания нижним его торцом поверхности воды. Считайте положение карандаша вертикальным. Плотность воды 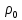 = 1000 кг\м3 = 1000 кг\м3
Оборудование: круглый карандаш, почти полная бутылка с водой, линейка.
Р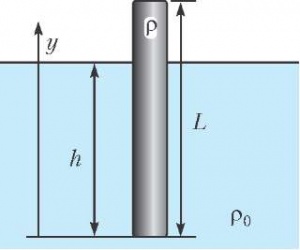 ешение. Опускаем карандаш в бутылку - он будет плавать, как поплавок. Пусть L - длина всего карандаша, V - его объем, h - длина погруженной в воду части карандаша, ешение. Опускаем карандаш в бутылку - он будет плавать, как поплавок. Пусть L - длина всего карандаша, V - его объем, h - длина погруженной в воду части карандаша, 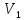 - ее объем, S - площадь сечения и d – диаметр карандаша. Найдем среднюю плотность карандаша ρ из условия плавания тела: - ее объем, S - площадь сечения и d – диаметр карандаша. Найдем среднюю плотность карандаша ρ из условия плавания тела:
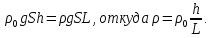
Предположим, что мы с постоянной скоростью вытаскиваем карандаш из воды, используя динамометр. Когда карандаш свободно плавает, динамометр показывает ноль. Если же карандаш полностью вытащить из воды, то динамометр покажет силу, равную весу Р карандаша:
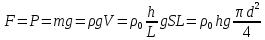
Получается, что показания динамометра при вытаскивании карандаша из воды изменяются от 0 до P по линейному закону. При этом механическая работа А будет равна площади выделенного треугольника:
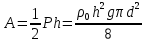 [20]. [20].
Задача 6. Высыпая соль или сахар в кипящую воду, можно заметить, что кипение ненадолго прекращается за счет снижения температуры воды. Определите количество теплоты, необходимое для растворения 1 кг пищевой соды в воде комнатной температуры.
Оборудование: самодельный калориметр, термометр, вода, сода, мерный цилиндр (стакан), груз известной массы (гайка массой 10 г), пластиковая ложка.
Решение. В задачу входит дополнительное конструкторское задание по изготовлению простого самодельного калориметра. Для внутреннего сосуда калориметра следует взять обычную алюминиевую банку объемом 0,33 л. У банки удаляется верхняя крышка так, чтобы получился алюминиевый стакан (массой всего 12 г) с жестким верхним ободком. Внутри верхнего ободка делается прорезь для того, чтобы вода полностью выливалась из банки. Внешняя пластмассовая оболочка изготавливается на основе пластиковой бутылки объемом 1,5 л. Бутылка разрезается на три части, верхняя часть удаляется, а средняя и нижняя части с некоторым усилием вставляются друг в друга и плотно фиксируют внутреннюю алюминиевую банку в вертикальном положении. (Если нет калориметра, то опыты можно проводить и в одноразовом пластиковом стаканчике, массой и теплопередачей которого можно пренебречь.)
Предварительно следует сделать два измерения: 1) определить, сколько соды помещается в ложку (для этого надо заглянуть в кулинарный справочник или «вычерпать» этой ложкой пакет соды известной массы); 2) определиться с количеством воды - в малом количестве воды раствор сразу же станет насыщенным и часть соды не растворится, в большом количестве воды температура изменится на доли градуса, что затруднит измерения.
Очевидно, что количество теплоты, необходимое для растворения вещества, пропорционально массе этого вещества: Q m . Для записи равенства следует ввести коэффициент пропорциональности, например z, который можно назвать «удельной теплотой растворения». Тогда Q=zm. Растворение соды осуществляется за счет энергии, выделяющейся при охлаждении сосуда с водой. Величина z находится из следующего уравнения теплового баланса:
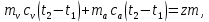
где 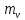 - масса воды в калориметре, - масса воды в калориметре, 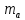 - масса внутреннего алюминиевого стакана калориметра, m - масса растворенной соды, ( - масса внутреннего алюминиевого стакана калориметра, m - масса растворенной соды, (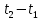 ) - понижение температуры в калориметре. Массу внутреннего сосуда калориметра можно легко найти, используя правило моментов сил, уравновесив сосуд и груз известной массы при помощи линейки и ниток [20]. ) - понижение температуры в калориметре. Массу внутреннего сосуда калориметра можно легко найти, используя правило моментов сил, уравновесив сосуд и груз известной массы при помощи линейки и ниток [20].
Задача 7. Определить плотность камня, если его объем невозможно измерить непосредственно.
Оборудование: весы, набор гирь, сосуд с водой.
Решение. Прежде всего, с помощью весов определим массу камня 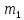 и найдем массу сосуда и найдем массу сосуда 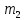 , доверху наполненного водой. После этого снимем сосуд с весов, положим в него камень (часть воды при этом выльется), вытащим камень и измерим , доверху наполненного водой. После этого снимем сосуд с весов, положим в него камень (часть воды при этом выльется), вытащим камень и измерим 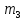 - массу сосуда с оставшейся водой. Нетрудно видеть, что разность - массу сосуда с оставшейся водой. Нетрудно видеть, что разность 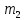 - - 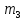 равна массе воды равна массе воды 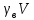 , вытесненной камнем: , вытесненной камнем:
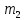 - - 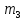 = = 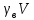 , ,
где 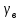 - плотность воды, а - плотность воды, а 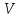 - объем камня. Поделив массу камня - объем камня. Поделив массу камня 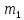 на его объем, найденный из последней формулы, получим искомую величину, равную на его объем, найденный из последней формулы, получим искомую величину, равную
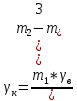 . .
Изложенный способ дает хорошие результаты, если объем камня не очень мал (точнее, близок к объему сосуда) [7].
Задача 8. Как с помощью гирьки известной массы, легкого шнура, двух гвоздей, молотка, кусочка пластилина, математических таблиц и транспортира определить массу некоторого предмета?
Р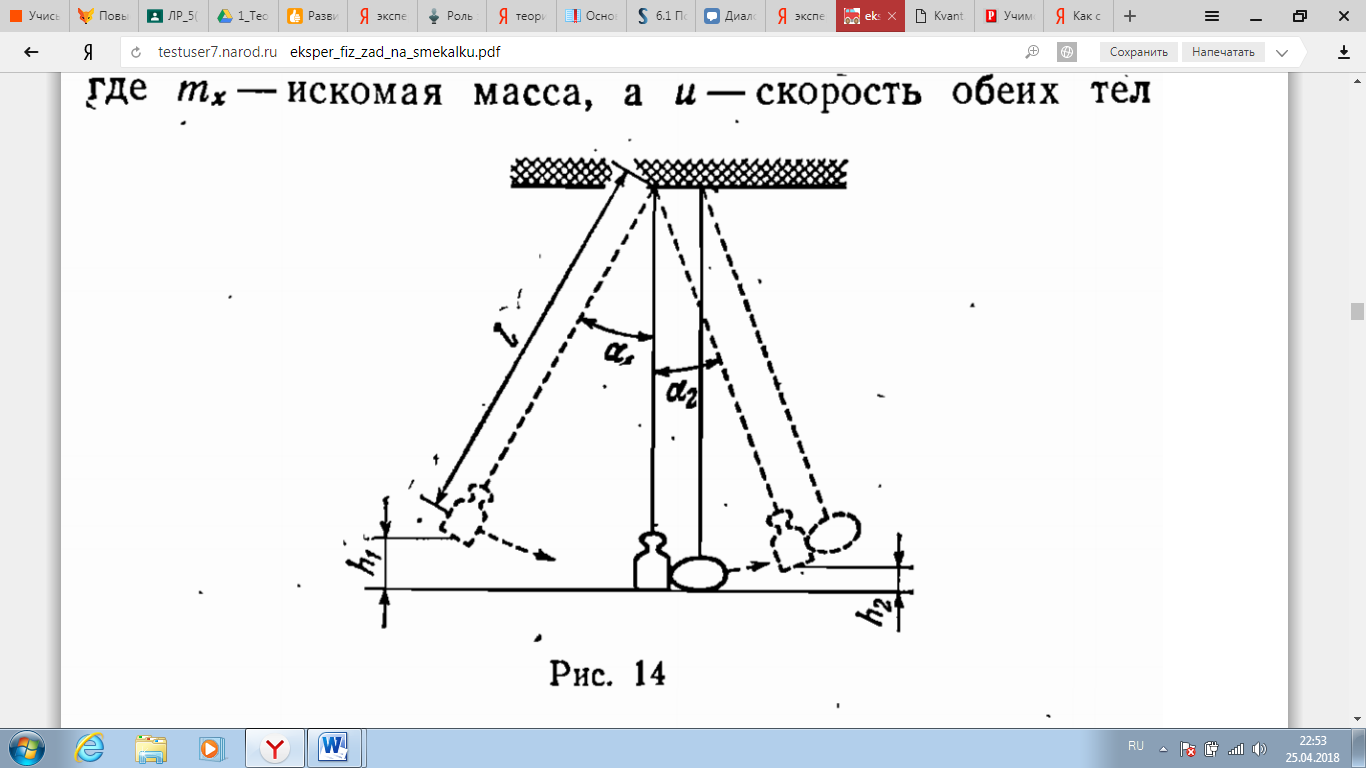 ешение. Подвесим гирьку известной массы и тело на шнурах так, чтобы они соприкасались, а шнурки были параллельны. Отклонив гирьку в плоскости, проходящей через оба подвеса, измерим транспортиром угол отклонения ешение. Подвесим гирьку известной массы и тело на шнурах так, чтобы они соприкасались, а шнурки были параллельны. Отклонив гирьку в плоскости, проходящей через оба подвеса, измерим транспортиром угол отклонения 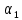 , затем прилепим с той стороны гирьки, которая обращена к телу, пластилин и выпустим ее из рук. Возвратившись в положение равновесия, гирька ударится о предмет, прилипнет к нему и дальше оба тела будут двигаться вместе, пока не отклонятся на некоторый угол , затем прилепим с той стороны гирьки, которая обращена к телу, пластилин и выпустим ее из рук. Возвратившись в положение равновесия, гирька ударится о предмет, прилипнет к нему и дальше оба тела будут двигаться вместе, пока не отклонятся на некоторый угол 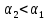 . Приравняв потенциальную энергию гирьки в отклоненном положении ее кинетической энергии: . Приравняв потенциальную энергию гирьки в отклоненном положении ее кинетической энергии:
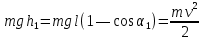
Где, m - масса гирьки, v - ее скорость в момент удара; смысл остальных обозначений ясен из рисунка. Найдем скорость и импульс гирьки перед соударением:
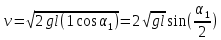 , ,
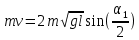 . .
Поскольку внешние силы, действующие в горизонтальном направлении, отсутствуют, закон сохранения импульса дает
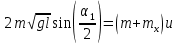 , ,
где 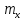 - искомая масса, а - искомая масса, а 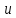 - скорость обеих тел после неупругого соударения. Отсюда скорость и кинетическая энергия системы непосредственно после удара равны - скорость обеих тел после неупругого соударения. Отсюда скорость и кинетическая энергия системы непосредственно после удара равны
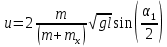 , ,
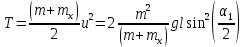 . .
Приравнивая кинетическую энергию потенциальной энергии тел после их отклонения на угол 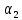 , получаем , получаем
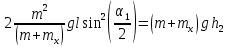 . .
Зная, что 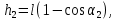 окончательно имеем окончательно имеем
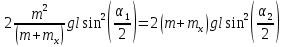 . .
Отсюда определяем нужную величину:
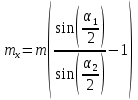 [7]. [7].
Задача 9. Один изобретатель предложил следующий способ для измерения скорости корабля. В каюте к потолку подвешен груз на нити. По мысли изобретателя в покоящемся корабле отвес должен располагаться вертикально, а в движущемся — наклонно к горизонту. По углу отклонения отвеса изобретатель и предложил измерять скорость корабля. Осуществим ли этот проект?
Решение. По углу отклонения груза от вертикали можно судить лишь об ускорении корабля, т. е. об изменении скорости. Скорость же равномерного прямолинейного движения таким способом определить нельзя, отвес при этом не отклонится от вертикали [9].
З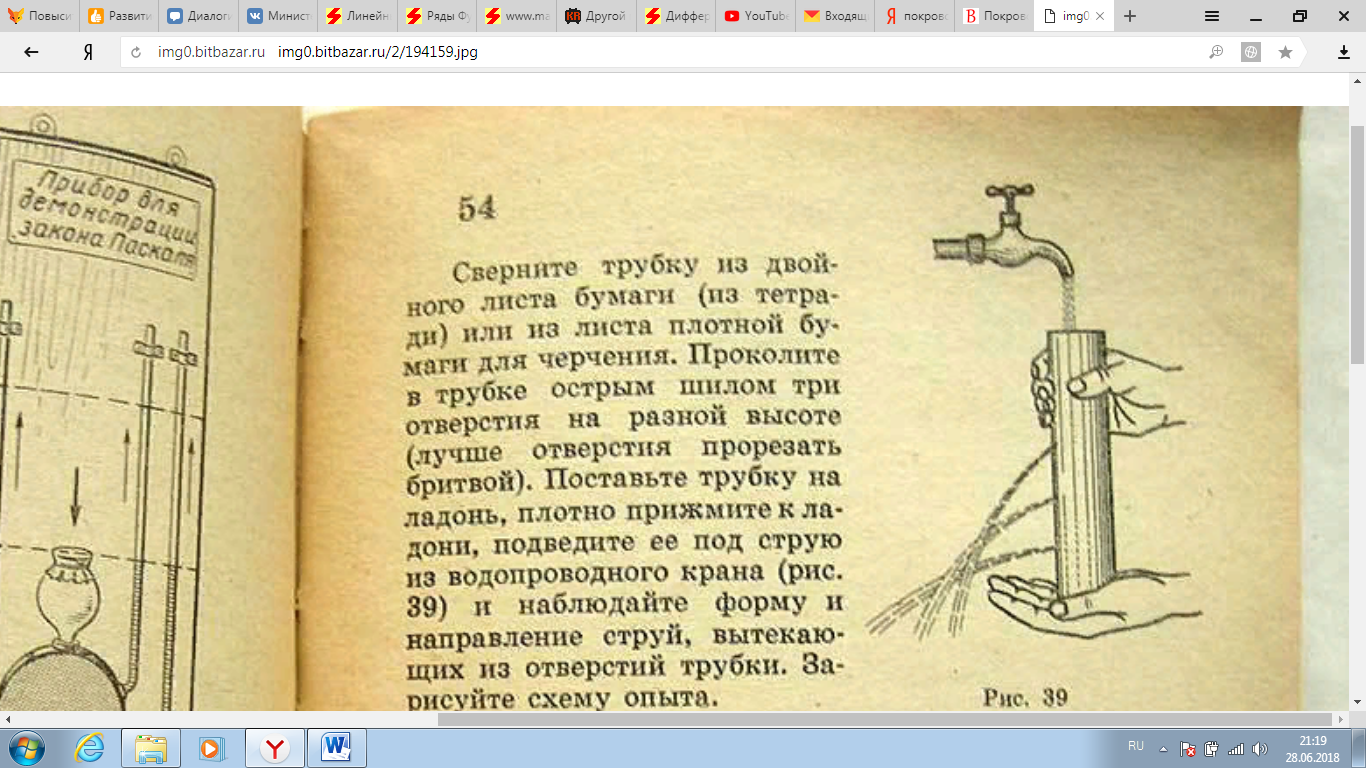 адача 10. Сверните трубку из двойного листа бумаги (из тетради) или из листа плотной бумаги для черчения. Проколите в трубке острым шилом три отверстия на разной высоте (лучше отверстия прорезать бритвой). Поставьте трубку на ладонь, плотно прижмите к ладони, подведите ее под струю из водопроводного крана и наблюдайте форму и направление струй, вытекающих из отверстий трубки. Зарисуйте схему опыта [8]. адача 10. Сверните трубку из двойного листа бумаги (из тетради) или из листа плотной бумаги для черчения. Проколите в трубке острым шилом три отверстия на разной высоте (лучше отверстия прорезать бритвой). Поставьте трубку на ладонь, плотно прижмите к ладони, подведите ее под струю из водопроводного крана и наблюдайте форму и направление струй, вытекающих из отверстий трубки. Зарисуйте схему опыта [8].
Задача 11. Измерение амплитуды, периода и циклической частоты колебаний груза, подвешенного на нити.
Приборы и материалы: шарик диаметром 25 мм на нити длинной 300 мм, линейка измерительная 30 см с миллиметровыми делениями, метроном электронный (один на класс).
Порядок выполнения работы:
П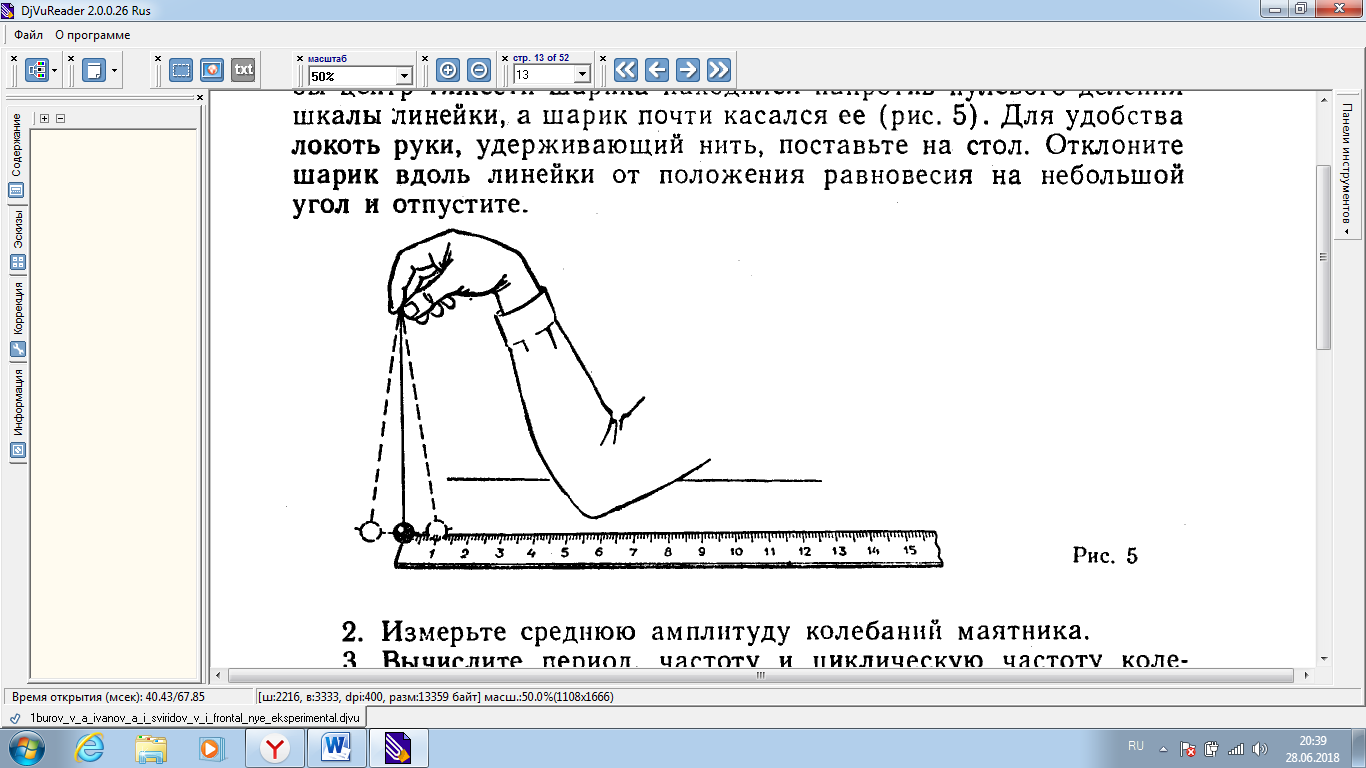 однимите шарик за конец нити над линейкой так, чтобы центр тяжести шарика находился напротив нулевого деления шкалы линейки, а шарик почти касался ее. Для удобства локоть руки, удерживающий нить, поставьте на стол. Отклоните шарик вдоль линейки от положения равновесия на небольшой угол и отпустите. однимите шарик за конец нити над линейкой так, чтобы центр тяжести шарика находился напротив нулевого деления шкалы линейки, а шарик почти касался ее. Для удобства локоть руки, удерживающий нить, поставьте на стол. Отклоните шарик вдоль линейки от положения равновесия на небольшой угол и отпустите.
Измерьте среднюю амплитуду колебаний маятника.
Вычислите период, частоту и циклическую частоту колебаний маятника.
Запишите уравнение колебаний маятника.
Зная амплитуду и циклическую частоту колебаний, вычислите смещение маятника через 2 секунды с момента начала колебаний.
Результаты измерений и вычислений запишите в тетрадь. [2]
Задача 12. Исследуйте процесс соударения двух монет, находящихся на листе бумаги, расположенном на горизонтальном столе. Определите величину механических потерь, их долю (в %) от полной энергии, полную энергию, скорость движения монеты непосредственно перед ударом.
Оборудование: лист миллиметровой бумаги, две пятикопеечные монеты образца 1961-1991 гг., масса которых 5 г ± 0.5%, линейка, транспортир.
Р ешение. На поверхности стола лежит пятикопеечная монета. На неё налетает такая же монета. Наша задача: определить потерю механической энергии при столкновении, если угол разлёта монет равен ешение. На поверхности стола лежит пятикопеечная монета. На неё налетает такая же монета. Наша задача: определить потерю механической энергии при столкновении, если угол разлёта монет равен 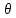 , коэффициент трения монет о стол равен , коэффициент трения монет о стол равен 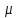 , а пути, которые они прошли после столкновения, равны , а пути, которые они прошли после столкновения, равны 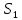 и и 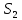 . Выберем систему координат, как показано на рисунке. Пусть . Выберем систему координат, как показано на рисунке. Пусть 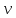 - скорость налетающей монеты до столкновения, - скорость налетающей монеты до столкновения, 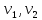 - скорости разлета монет сразу после столкновения, причём - скорости разлета монет сразу после столкновения, причём 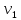 - скорость первоначально покоящейся монеты. - скорость первоначально покоящейся монеты.
Закон сохранения импульса для соударяющихся монет в выбранной системе координат имеет вид:
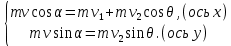 (1) (1)
Закон сохранения энергии
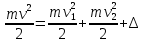 , (2) , (2)
где 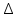 - потери механической энергии во время удара. Возводя каждое уравнение системы (1) в квадрат и складывая их, получим с учётом уравнения (2): - потери механической энергии во время удара. Возводя каждое уравнение системы (1) в квадрат и складывая их, получим с учётом уравнения (2):
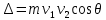 . .
Скорости 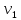 и и 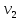 определим из условия того, что после удара вся механическая энергия монет переходит в тепло в результате совершения работы против сил трения: определим из условия того, что после удара вся механическая энергия монет переходит в тепло в результате совершения работы против сил трения:
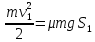 , ,
откуда
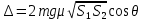 . .
Вся механическая энергия до удара равна
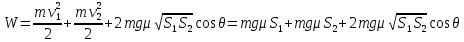 . .
Доля потерь механической энергии составляет:
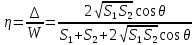 . .
Наконец, скорость монеты непосредственно перед ударом определится
соотношением:
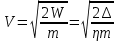 . .
Экспериментально осуществляется нецентральное соударение монет и измеряются пути 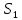 и и 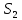 , а также угол , а также угол 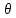 непосредственно на листе бумаги [8]. непосредственно на листе бумаги [8].
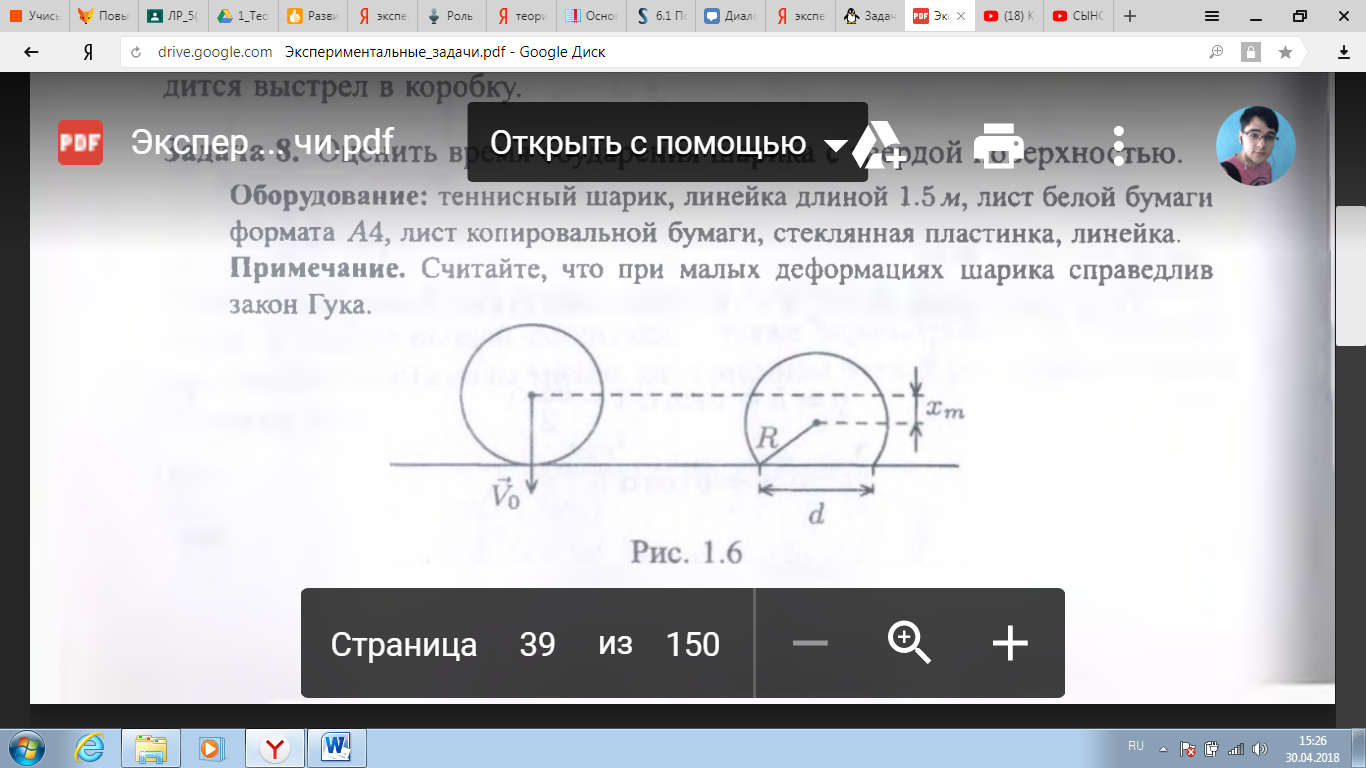
Задача 13. Оценить время соударения шарика с твёрдой поверхностью.
Оборудование: теннисный шарик, линейка длиной 1.5 м., лист белой бумаги формата А4, лист копировальной бумаги, стеклянная пластинка, линейка.
Примечание. Считайте, что при малых деформациях шарика справедлив закон Гука.
Решение. В предположении справедливости закона Гука процесс деформации шарика при соприкосновении с поверхностью соответствует полупериоду гармонического колебания. Время соударения 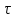 можно определить как можно определить как
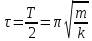 , ,
где 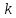 - жёсткость шарика, - жёсткость шарика, 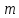 - его масса. - его масса.
Считая соударение абсолютно упругим, запишем закон сохранения энергии
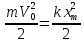 , ,
где 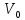 – скорость шарика в начале деформации, – скорость шарика в начале деформации, 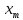 – максимальная деформация шарика. Тогда – максимальная деформация шарика. Тогда
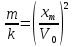 , ,
и для времени соударения получим выражение:
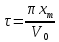 . .
Таким образом, для определения времени соударения достаточно знать скорость шарика перед соприкосновением с плоскостью и максимальную деформацию. Деформация 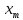 определяется так: на стеклянную пластинку кладутся листы белой, а на них - листы копировальной бумаги. Шарик, падая на копировальную бумагу, оставляет оттиск на белой бумаге. Измерив диаметр определяется так: на стеклянную пластинку кладутся листы белой, а на них - листы копировальной бумаги. Шарик, падая на копировальную бумагу, оставляет оттиск на белой бумаге. Измерив диаметр 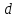 пятна образовавшегося на белой бумаге после удара, величину максимальной деформации вычисляют из геометрических соображений (см. рис.): пятна образовавшегося на белой бумаге после удара, величину максимальной деформации вычисляют из геометрических соображений (см. рис.):
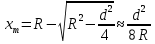 , ,
где R - радиус шарика, который можно определить, обернув вокруг него
в 1-2 слоя лист бумаги.
Для оценки скорости 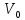 измеряют измеряют 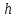 - высоту подскока после удара (начальная высота, с которой падал шарик, - - высоту подскока после удара (начальная высота, с которой падал шарик, - 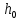 ). Для процессов падения шарика и подъёма его после удара справедливы соотношения: ). Для процессов падения шарика и подъёма его после удара справедливы соотношения:
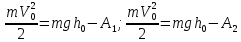 , (1) , (1)
где 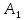 и и 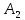 - работы сил сопротивления на соответствующих участках. Поскольку сила сопротивления, будучи функцией скорости, на обоих участках изменяется в одинаковых пределах, а совершаемые перемещения различны, можно записать - работы сил сопротивления на соответствующих участках. Поскольку сила сопротивления, будучи функцией скорости, на обоих участках изменяется в одинаковых пределах, а совершаемые перемещения различны, можно записать 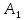 > > 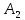 - Тогда с учётом (1): - Тогда с учётом (1):
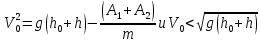 . .
С другой стороны, используя очевидное неравенство
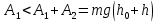 , ,
получаем оценку скорости 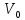 снизу: снизу: 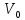 > > 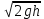 . .
Окончательно для оценки времени соударения имеем:
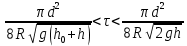 . .
Для проверки справедливости закона Гука достаточно убедиться в изохронности колебаний, то есть в независимости времени соударения 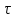 от высоты поднятия от высоты поднятия 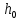 (необходимо провести второе измерение (необходимо провести второе измерение 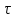 для другой высоты) [8]. для другой высоты) [8].
Задача 14. Определить жесткость резинового шнура.
Оборудование: два штатива с лапками, резиновый шнур, грузы известной массы, линейка.
Решение. Закрепим шнур, имеющий длину 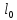 , между двумя штативами и подвесим к его середине груз массой , между двумя штативами и подвесим к его середине груз массой 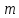 . Условие равновесия для указанной системы (рис.) в проекции на вертикальное направление (ось y) запишется в виде: . Условие равновесия для указанной системы (рис.) в проекции на вертикальное направление (ось y) запишется в виде:
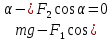 . (1) . (1)
Исходя из условия симметрии имеем: 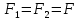 . .
Т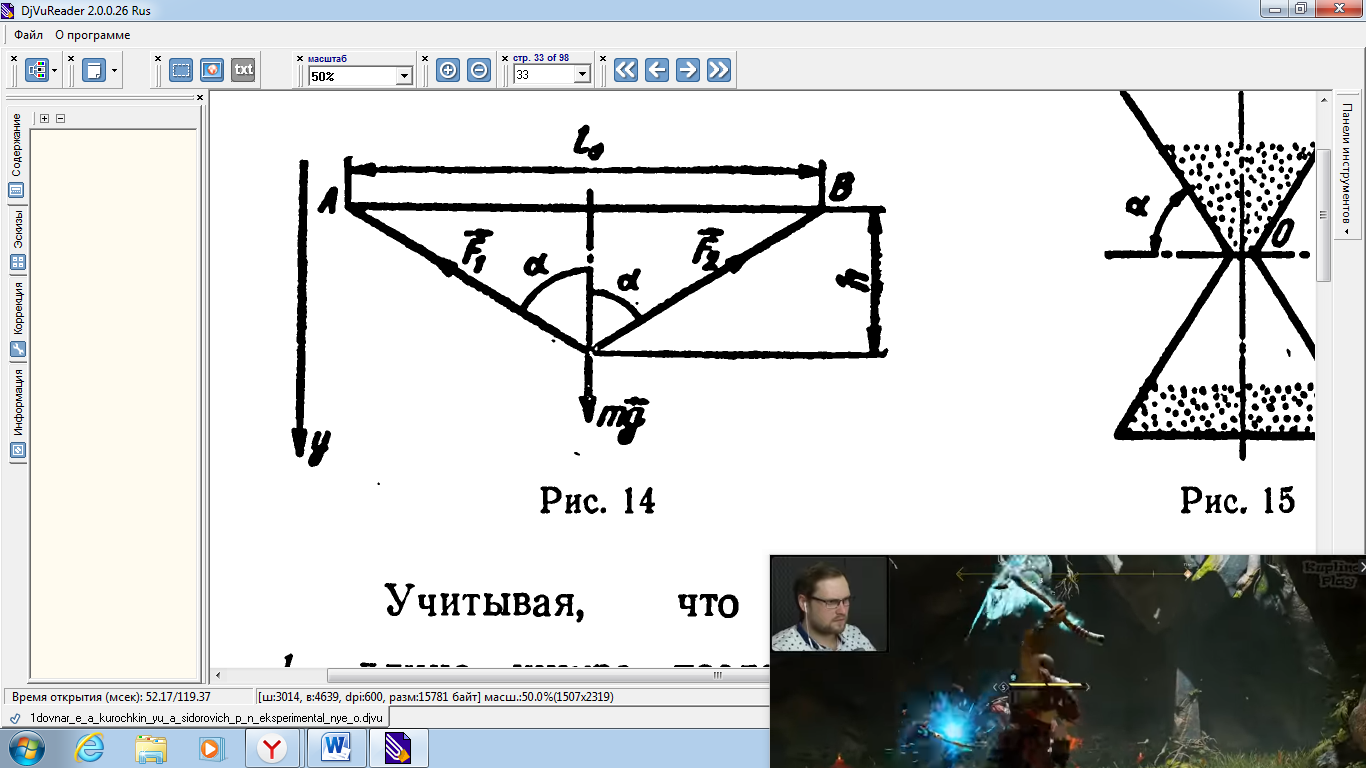 огда формула (1) запишется в виде: огда формула (1) запишется в виде: 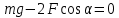 . .
Учитывая, что 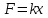 , где , где 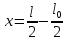 , , 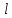 – длина шнура после растяжения его грузиком, а – длина шнура после растяжения его грузиком, а 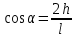 , получим: , получим: 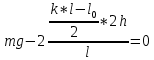 . .
Отсюда
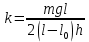 . .
Величины 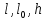 измеряются линейкой. Опыты необходимо проделать с различными грузиками [4]. измеряются линейкой. Опыты необходимо проделать с различными грузиками [4].
Задача 15. Стреляя из баллистического пистолета, установленного на столе, попадите, произведя только два выстрела, в картонную коробку, стоящую на полу (на столе).
Оборудование: баллистический пистолет, рулетка, коробка.
Примечание. Вначале разрешается произвести любое число выстрелов. Затем устанавливается коробка и разрешается произвести только два выстрела.
Р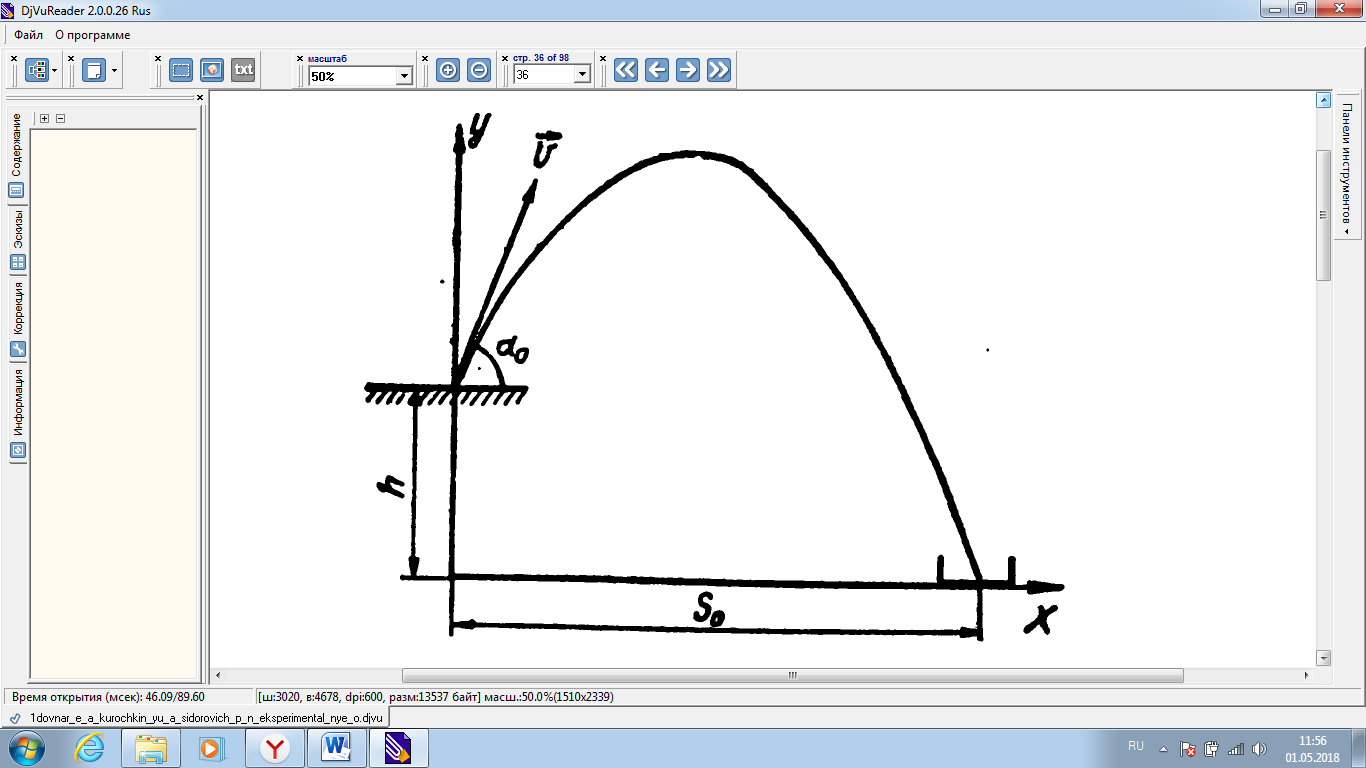 ешение. Установим баллистический пистолет под углом ешение. Установим баллистический пистолет под углом 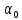 к плоскости стола и произведем выстрел из него (рис.). По известному расстоянию и высоте стола находим начальную скорость «снаряда», вылетающего из пистолета. к плоскости стола и произведем выстрел из него (рис.). По известному расстоянию и высоте стола находим начальную скорость «снаряда», вылетающего из пистолета.
Запишем уравнения изменения координат снаряда со временем (уравнение движения):
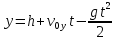 , (1) , (1)
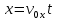 , (2) , (2)
где 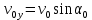 и и 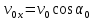 . .
Подставив значения 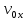 и и 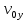 в выражение (1) и (2), имеем: в выражение (1) и (2), имеем:
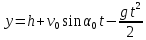 , (3) , (3)
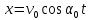 . (4) . (4)
Выразив из уравнения (4) время 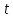 и подставив его значение в выражение (3) с учетом того, что в момент падения и подставив его значение в выражение (3) с учетом того, что в момент падения 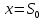 , , 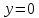 , получим: , получим:
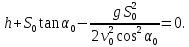 (5) (5)
После несложных преобразований находим, что
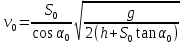 . .
Зная значения 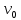 и измерив расстояние и измерив расстояние 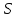 от стола до коробки (по горизонтали), мы можем рассчитать значение угла от стола до коробки (по горизонтали), мы можем рассчитать значение угла 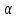 , под которым надо установить пистолет, чтобы попасть в коробку. Для этого в выражение (5) вместо , под которым надо установить пистолет, чтобы попасть в коробку. Для этого в выражение (5) вместо 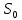 и и 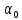 подставим подставим 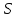 и и 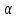 , после чего оно примет вид: , после чего оно примет вид:
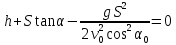 . (6) . (6)
Рассматривая выражение (6) как тригонометрическое уравнение для определения 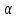 и решив его, находим, что и решив его, находим, что
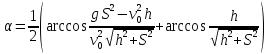 . .
Установив пистолет под рассчитанным углом 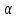 , произведем выстрел в коробку. , произведем выстрел в коробку.
Возможно также проведение серии выстрелов вертикально вверх или горизонтально с целью нахождения средней скорости вылета снаряда и пределов отклонения скорости от этого значения. По пределам отклонения скоростей можно оценить область попадания. Если размеры коробки больше размеров области попадания, производят 2 выстрела. Второй выстрел предлагается во избежание случайного резкого отклонения скорости снаряда от средней величины [4].
Задача 16. Возьмите диск из металла, фанеры или пластмассы диаметром 10 см. По его размерам вырежьте кружок из бумаги. В одну руку возьмите бумажный диск, в другую – металлический (фанерный, пластмассовый) и предоставьте им возможность свободно падать с одной и той же высоты.
Почему металлический диск падает быстрее бумажного?
Положите бумажный диск на металлический и дайте им возможность свободно падать. Почему в этом случае они падают одновременно?
Решение: На каждый из дисков действуют две силы: сила тяжести и сила сопротивления воздуха. В начале движения равнодействующая этих сил, направленная вниз, больше для металлического диска, поэтому он будет двигаться с большим ускорением. Но с увеличением скорости сила сопротивления воздуха увеличивается и становится равной силе тяжести. В итоге оба диска будут двигаться равномерно, но металлический диск – с большей скоростью.
Во втором случае сопротивление воздуха преодолевает только металлический диск, а сила тяжести сообщает обоим телам равные ускорения, не зависящие от масс [2].
Задача 17. Установка: Два ведра, одно из которых наполнено водой, другое – песком (или землей), вес которого равен весу воды.
Условие задачи: Возьмите ведро с водой за середину ручки, например, в левую руку, а ведро с песком – в правую и начните, опустив руки с ведрами, быстро поворачивать кисти рук то в одну, то в другую сторону. Ведро с водой послушно будет следовать за движением вашей руки. С другим ведром вам этого никак не удастся проделать. Почему же, несмотря на то, что масса одного ведра и его содержимого равна массе другого, первое легко поворачивается в одну и другую сторону, а другое – нет?
Дополнение: Получится ли одинаковый эффект с железными ведрами, в одно из которых налита вода, а в другое – равное по весу количество ртути?
Решение: Вращающиеся массы различны. В первом случае вращается практически только само ведро. (Начинает вращаться тонкий слой воды непосредственно около стенок. Остальная масса остается в покое вследствие весьма незначительного внутреннего трения.) Второе же ведро, с песком, вращается как одно целое. Вследствие этого во втором случае силы инерции значительнее, чем в первом.
Дополнение: Нет. Стенки железного ведра смачиваются водой, но не смачиваются ртутью. Поэтому вместе с первым ведром будет вращаться тонкий слой воды, а вместе со вторым ведром слой ртути вращаться не будет. Легче вращать в одну и в другую сторону, как указано в задаче, ведро со ртутью [5].
|
|
|
 Скачать 2.66 Mb.
Скачать 2.66 Mb.
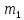 к нити длиной
к нити длиной 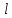 , отведем его на измеряемый транспортиром угол
, отведем его на измеряемый транспортиром угол 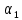 и отпустим.
и отпустим.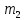 , к которому прикрепим кусочек пластилина массой Δm.
, к которому прикрепим кусочек пластилина массой Δm. ри своем движении шарик массой
ри своем движении шарик массой 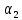 .При этом выполняется закон сохранения импульса:
.При этом выполняется закон сохранения импульса: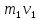
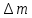 )
)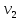 .
.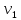 шарика известной массы в момент соударения находим из закона сохранения механической энергии
шарика известной массы в момент соударения находим из закона сохранения механической энергии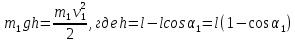
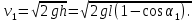
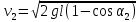
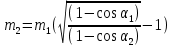
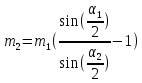
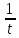 , (1)
, (1)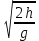 . (2)
. (2)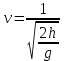
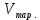 Аккуратно опустим брусок в пластиковую тарелку с водой. Объем вытесненной воды
Аккуратно опустим брусок в пластиковую тарелку с водой. Объем вытесненной воды 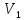 определим с помощью мерного стакана. Аккуратно погрузим весь брусок в воду. Некоторая часть воды вновь выльется из тарелки. Ясно, что всего из тарелки будет вытеснен объем воды равный объему бруска
определим с помощью мерного стакана. Аккуратно погрузим весь брусок в воду. Некоторая часть воды вновь выльется из тарелки. Ясно, что всего из тарелки будет вытеснен объем воды равный объему бруска 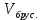 .
. 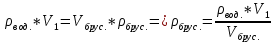 Несмотря на идейную простоту, задача требует известного экспериментального искусства и внимательности: объем воды умещающийся в тарелке оказывается больше объема тарелки, т. к. заметная часть воды "возвышается" над краем тарелки за счет сил поверхностного натяжения. Небрежно выполненный эксперимент приводит к ощутимой ошибке в определении плотности дерева [17].
Несмотря на идейную простоту, задача требует известного экспериментального искусства и внимательности: объем воды умещающийся в тарелке оказывается больше объема тарелки, т. к. заметная часть воды "возвышается" над краем тарелки за счет сил поверхностного натяжения. Небрежно выполненный эксперимент приводит к ощутимой ошибке в определении плотности дерева [17].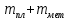 ), массу чистого пластилина
), массу чистого пластилина 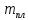 и по их разности - массу металла
и по их разности - массу металла 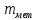 , находящегося в одном из кусков пластилина. Взвесив данные куски пластилина сначала в воздухе, а потом в воде, можно найти выталкивающую силу и, зная плотность воды, можно вычислить объемы кусков (
, находящегося в одном из кусков пластилина. Взвесив данные куски пластилина сначала в воздухе, а потом в воде, можно найти выталкивающую силу и, зная плотность воды, можно вычислить объемы кусков (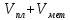 ) и
) и 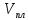 . Объем металла
. Объем металла 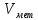 можно определить по разности этих объемов.
можно определить по разности этих объемов.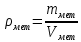 .
.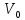 . Плотность металла можно найти, решив следующую систему четырех уравнений с четырьмя неизвестными:
. Плотность металла можно найти, решив следующую систему четырех уравнений с четырьмя неизвестными: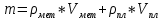
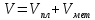
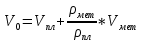
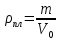
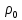 = 1000 кг\м3
= 1000 кг\м3 ешение. Опускаем карандаш в бутылку - он будет плавать, как поплавок. Пусть L - длина всего карандаша, V - его объем, h - длина погруженной в воду части карандаша,
ешение. Опускаем карандаш в бутылку - он будет плавать, как поплавок. Пусть L - длина всего карандаша, V - его объем, h - длина погруженной в воду части карандаша, 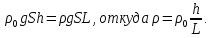
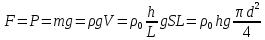
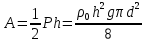
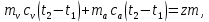
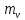 - масса воды в калориметре,
- масса воды в калориметре, 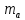 - масса внутреннего алюминиевого стакана калориметра, m - масса растворенной соды, (
- масса внутреннего алюминиевого стакана калориметра, m - масса растворенной соды, (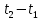 ) - понижение температуры в калориметре. Массу внутреннего сосуда калориметра можно легко найти, используя правило моментов сил, уравновесив сосуд и груз известной массы при помощи линейки и ниток [20].
) - понижение температуры в калориметре. Массу внутреннего сосуда калориметра можно легко найти, используя правило моментов сил, уравновесив сосуд и груз известной массы при помощи линейки и ниток [20].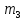 - массу сосуда с оставшейся водой. Нетрудно видеть, что разность
- массу сосуда с оставшейся водой. Нетрудно видеть, что разность 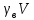 , вытесненной камнем:
, вытесненной камнем: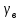 - плотность воды, а
- плотность воды, а 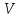 - объем камня. Поделив массу камня
- объем камня. Поделив массу камня 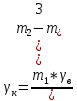
 ешение. Подвесим гирьку известной массы и тело на шнурах так, чтобы они соприкасались, а шнурки были параллельны. Отклонив гирьку в плоскости, проходящей через оба подвеса, измерим транспортиром угол отклонения
ешение. Подвесим гирьку известной массы и тело на шнурах так, чтобы они соприкасались, а шнурки были параллельны. Отклонив гирьку в плоскости, проходящей через оба подвеса, измерим транспортиром угол отклонения 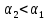 . Приравняв потенциальную энергию гирьки в отклоненном положении ее кинетической энергии:
. Приравняв потенциальную энергию гирьки в отклоненном положении ее кинетической энергии: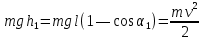
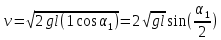
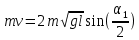
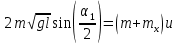
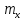 - искомая масса, а
- искомая масса, а 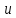 - скорость обеих тел после неупругого соударения. Отсюда скорость и кинетическая энергия системы непосредственно после удара равны
- скорость обеих тел после неупругого соударения. Отсюда скорость и кинетическая энергия системы непосредственно после удара равны 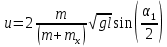
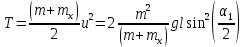
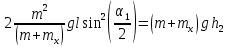
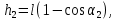 окончательно имеем
окончательно имеем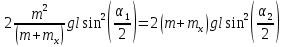
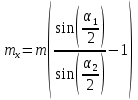
 адача 10.
адача 10.  однимите шарик за конец нити над линейкой так, чтобы центр тяжести шарика находился напротив нулевого деления шкалы линейки, а шарик почти касался ее. Для удобства локоть руки, удерживающий нить, поставьте на стол. Отклоните шарик вдоль линейки от положения равновесия на небольшой угол и отпустите.
однимите шарик за конец нити над линейкой так, чтобы центр тяжести шарика находился напротив нулевого деления шкалы линейки, а шарик почти касался ее. Для удобства локоть руки, удерживающий нить, поставьте на стол. Отклоните шарик вдоль линейки от положения равновесия на небольшой угол и отпустите. ешение. На поверхности стола лежит пятикопеечная монета. На неё налетает такая же монета. Наша задача: определить потерю механической энергии при столкновении, если угол разлёта монет равен
ешение. На поверхности стола лежит пятикопеечная монета. На неё налетает такая же монета. Наша задача: определить потерю механической энергии при столкновении, если угол разлёта монет равен 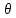 , коэффициент трения монет о стол равен
, коэффициент трения монет о стол равен 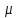 , а пути, которые они прошли после столкновения, равны
, а пути, которые они прошли после столкновения, равны 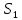 и
и 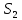 . Выберем систему координат, как показано на рисунке. Пусть
. Выберем систему координат, как показано на рисунке. Пусть 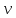 - скорость налетающей монеты до столкновения,
- скорость налетающей монеты до столкновения, 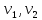 - скорости разлета монет сразу после столкновения, причём
- скорости разлета монет сразу после столкновения, причём 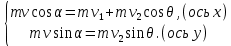
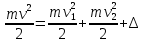
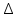 - потери механической энергии во время удара. Возводя каждое уравнение системы (1) в квадрат и складывая их, получим с учётом уравнения (2):
- потери механической энергии во время удара. Возводя каждое уравнение системы (1) в квадрат и складывая их, получим с учётом уравнения (2):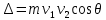
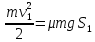
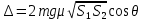
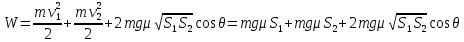
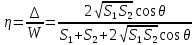
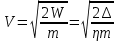

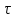 можно определить как
можно определить как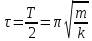
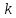 - жёсткость шарика,
- жёсткость шарика, 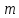 - его масса.
- его масса.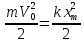
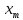 – максимальная деформация шарика. Тогда
– максимальная деформация шарика. Тогда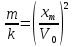
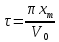
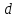 пятна образовавшегося на белой бумаге после удара, величину максимальной деформации вычисляют из геометрических соображений (см. рис.):
пятна образовавшегося на белой бумаге после удара, величину максимальной деформации вычисляют из геометрических соображений (см. рис.):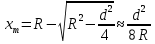
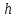 - высоту подскока после удара (начальная высота, с которой падал шарик, -
- высоту подскока после удара (начальная высота, с которой падал шарик, - 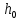 ). Для процессов падения шарика и подъёма его после удара справедливы соотношения:
). Для процессов падения шарика и подъёма его после удара справедливы соотношения: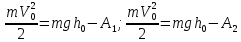
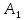 и
и 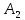 - работы сил сопротивления на соответствующих участках. Поскольку сила сопротивления, будучи функцией скорости, на обоих участках изменяется в одинаковых пределах, а совершаемые перемещения различны, можно записать
- работы сил сопротивления на соответствующих участках. Поскольку сила сопротивления, будучи функцией скорости, на обоих участках изменяется в одинаковых пределах, а совершаемые перемещения различны, можно записать 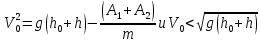
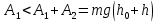
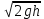 .
.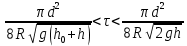
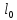 , между двумя штативами и подвесим к его середине груз массой
, между двумя штативами и подвесим к его середине груз массой 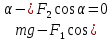
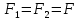 .
. огда формула (1) запишется в виде:
огда формула (1) запишется в виде: 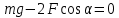 .
.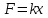 , где
, где 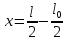 ,
, 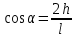 , получим:
, получим: 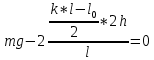 .
.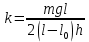
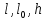 измеряются линейкой. Опыты необходимо проделать с различными грузиками [4].
измеряются линейкой. Опыты необходимо проделать с различными грузиками [4]. ешение. Установим баллистический пистолет под углом
ешение. Установим баллистический пистолет под углом 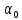 к плоскости стола и произведем выстрел из него (рис.). По известному расстоянию и высоте стола находим начальную скорость «снаряда», вылетающего из пистолета.
к плоскости стола и произведем выстрел из него (рис.). По известному расстоянию и высоте стола находим начальную скорость «снаряда», вылетающего из пистолета.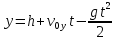
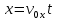
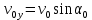 и
и 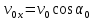 .
.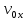 и
и 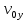 в выражение (1) и (2), имеем:
в выражение (1) и (2), имеем: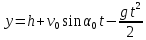
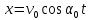
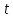 и подставив его значение в выражение (3) с учетом того, что в момент падения
и подставив его значение в выражение (3) с учетом того, что в момент падения 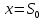 ,
, 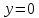 , получим:
, получим: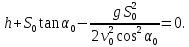
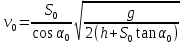
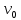 и измерив расстояние
и измерив расстояние 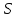 от стола до коробки (по горизонтали), мы можем рассчитать значение угла
от стола до коробки (по горизонтали), мы можем рассчитать значение угла 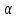 , под которым надо установить пистолет, чтобы попасть в коробку. Для этого в выражение (5) вместо
, под которым надо установить пистолет, чтобы попасть в коробку. Для этого в выражение (5) вместо 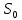 и
и