Теоретическое обоснование. Курсовая работа термодинамические и кинетические особенности пиролиза углеводородов

• Название: Курсовая работа термодинамические и кинетические особенности пиролиза углеводородов
• Дата: 15.05.2023
• Размер: 151.29 Kb.
• Имя файла: Теоретическое обоснование.docx
• Тип: Курсовая; #1133263
• страница: 2 из 3

определение параметров кинетического уравнения

рассмотрим простую реакцию типа

A₁  A₂  продукты.

кинетическое уравнение для такой реакции имеет вид

w kc^1 c^2 .

(2.14)

V A₁ A₂

параметрами кинетического уравнения являются частные


2

1
порядки реакции по компонентам ( и  ), величина константы

скорости реакции (k), величина энергии активации (E_а) и предэк- споненциальный множитель (k_о).

при определении частного порядка реакции по одному из

компонентов необходимо провести реакцию таким образом, чтобы концентрация другого в течение определения не изменялась. Это возможно, если использовать прием, называемый методом изоли-рованияОствальдаили методомизбытков[8].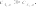

зададим начальную концентрацию одного из исходных веществ (например, A₁) гораздо большую, чем концентрацию дру- гого: поскольку глубина реакции х одинакова и для первого, и для второго вещества, при сравнении текущих концен- траций первого и второго вещества можно утверждать, что теку- щая концентрация первого вещества практически осталась равной его начальной концентрации и будет и дальше постоянной в тече- ние реакции.


2 2

1 1 1
с_A  c_{A ,o}  ₂ x; с_A  c_{A ,o}  ₁x c_{A ,o}.
теперь закон скорости можно преобразовать следующим образом:

w k^эф (с  x)^2 ,

V A₂ ,o 2

где под величиной эффективной константы скорости (k^эф) подра- зумевается произведение константы скорости на начальную кон- центрацию первого компонента в соответствующей степени: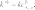

интегральные методы определения порядков реакций. Эти методы основаны на применении интегрального кинетиче- ского уравнения. их преимущество в том, что они используют пер- вичные данные (концентрация — время), полученные непосред- ственно из опыта. при этом достигается усреднение константы скорости. различают несколько интегральных методов.

с по соб по дст ановк и. позволяет установить соответ- ствие опытных данных одному из интегральных кинетических уравнений для целочисленных порядков (от 0 до 2). Можно этот способ осуществлять алгебраически, а можно графически. в пер- вом случае при обработке массива кинетических данных прово- дится расчет константы скорости реакции последовательно для разных порядков. если, например, для реакций первого порядка рассчитанные значения константы скорости монотонно убывают или возрастают, то делают вывод о непригодности данного кине- тического уравнения и переходят к проверке следующего. если подобрали такое кинетическое уравнение, по расчету из которого значения констант скорости колеблются около постоянной вели- чины (с учетом ошибки определения самих экспериментальных величин), то делают вывод, что исследуемая реакция в целом имеет такой порядок.

Может так случиться, что ни одно из кинетических уравнений не подойдет, тогда делают вывод о сложности реакции, порядок которой не равен целому числу, и начинают другими методами определять этот порядок.

считается, что метод подстановки надежен, если степень превращения в реакции достигает 70–90 % или, иначе, при доста- точно длительном времени реакции.

Графический вариант этого метода состоит в построении для реакций 0–2 порядков линейных анаморфоз кинетических кри- вых в соответствующих каждому порядку реакции координатах. вывод о том или ином порядке делается по тому, линеаризиру- ются ли экспериментальные данные в определенных координатах. на рис. 2.1–2.2 приведены виды графических зависимостей при совпадении порядка с предполагаемым. еще раз нужно отметить,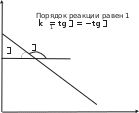

что в случае участия нескольких веществ в реакции их концентра- ции берутся одинаковыми.
ln(c_o − x)


τ

рис. 2.1

1/(с_o− x)
Порядок реакции равен 2

tg  = k₂


1/с_o


рис. 2.2
в случае если опытные данные располагаются вдоль пря- мой, это подтверждает предположение о данном порядке реакции

и позволяет по угловому наклону этой прямой определить вели- чину константы скорости реакции.

о пре деление порядк а ре акции по времени по лупревращени я. для характеристики реакционных про- цессов часто используют понятие время полупревращения; — время, необходимое для превращения половины исходного коли- чества реагирующего вещества.

Математическое выражение для времени полупревращения находят путем подстановки в интегральные уравнения реакций

разных порядков значения плотности глубины, равной

известно, что время полупревращения для реакции порядка 

выражается следующим образом:

_{1 2} 

₂1 _1


о
( 1)k(c)^{1 .}
(2.15)

преобразуем эту формулу к виду

_{1 2} (c_o )
1

₂1 _1



.

( 1)k
(2.16)

проведем два опыта, различающихся только начальной кон- центрацией реагента: в одном опыте начальная концентрация равна (c_o )₁, а во втором (c_o )₂. правая часть выражения (2.16) будет одинаковой, т. е.

( ) (c)^1  ( ) (c)^1.

1 2 1 o 1 1 2 2 o 2
логарифмирование этого соотношения позволит алгебраиче- ским путем вычислить порядок реакции по формуле



ln ^__{1 2  }_{1 2 } ^

  1^{2 1} .

(2.17)

1 
^{ln }_^сo  ₂ ^сo  ^

очевидно, что этим способом можно определить любые вели- чины порядка реакции, включая дробные и отрицательные.

что касается реакций первого порядка, то, как известно, время полупревращения в этом случае не зависит от концентра- ции исходного вещества. следовательно, без всяких дополнитель- ных расчетов можно сделать вывод о первом порядке исследуемой реакции, если определенное экспериментально по кинетической кривой время полупревращения исходного вещества не зависит от начальной концентрации.

дифференциальный метод определения порядка реакции. запишем основной постулат химической кинетики для реакции, в которой применен метод изолирования оствальда. в данной серии опытов определяется частный порядок реакции по одному из реагентов, например по A₂:

A
w k^эфc^2 .

2

(2.18)

прологарифмировав уравнение (2.18), мы получим линейную зависимость логарифма скорости от логарифма концентрации

2 A
ln w ln k^эф   ln c .

2

(2.19)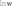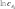

уравнение (2.19) позволяет использовать графический вари- ант данного метода. для этого строят зависимость от . из тангенса угла наклона полученной прямой определяют порядок реакции, а из отсекаемого на оси ординат отрезка — константу скорости. различные значения от могут быть получены из одной кинетической кривой, однако более надежные резуль- таты (с учетом ошибок эксперимента) получают, используя значе- ния начальных скоростей при разных начальных концентрациях реагентов.

в первом случае по одной кинетической кривой в разные моменты времени определяют концентрацию вещества и, проведя касательные к точке, соответствующей этой концентрации, нахо- дят скорость реакции. во втором случае проводят серию опытов, отличающихся друг от друга лишь начальной концентрацией веще- ства A₂. для определения частных порядков реакции в этом случае учитывают только прямолинейные начальные участки кинетиче- ских кривых и соответственно начальную скорость реакции.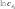

графическая зависимость логарифма скорости реакции от логарифма концентрации реагента позволит определить в соответ- ствии с уравнением (2.19) частный порядок реакции. а отрезок, отсекаемый прямой на оси ординат при нулевом значении , позволит определить константу скорости реакции. типичный вид такой зависимости приведен на рис. 2.3.

ln w

рис. 2.3

ln c_A2