работа олега. работа Олега. Курсовая работа учебная дисциплина Теория электрической связи
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-Бруевича» __________________________________________________________ Факультет многоканальных телекоммуникационных систем Кафедра «Теоретических основ радиотехники и телепередачи» КУРСОВАЯ РАБОТА учебная дисциплина «Теория электрической связи» Тема: «Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции» Выполнил студент II курса группы ИКТК-96 Морозов О., номер по списку группы:15 вариант №15 Проверил руководитель Денисов А.В. Оценка __________(подпись) Санкт-Петербург - 2021 ОГЛАВЛЕНИЕ 1. Структурная схема системы цифровой связи 3 2. Исходные данные 5 3. Расчёт основных характеристик системы передачи цифровой информации 5 3.1. Источник сообщения 5 3.2. Аналого-цифровой преобразователь 7 3.3. Кодер 8 3.4. Формирователь модулирующих символов 9 3.5. Модулятор 12 3.5.1. Сглаживающий формирующий фильтр 12 3.5.2. Блоки перемножителей, инвертор, сумматор 15 3.6. Непрерывный канал 17 3.7. Демодулятор 18 3.8. Декодер 21 Список литературы 24 1. Структурная схема системы цифровой связи Рис. 1. Структурная схема системы цифровой связи Назначение всех функциональных узлов цифровой системы связи (ЦСС): 1 – источник сообщений создает реализации a(t) случайного процесса A(t); 2 – аналого-цифровой преобразователь (АЦП) преобразует аналоговый сигнал от источника сообщения в последовательность его двоичных цифровых отсчётов; 3 – кодер (К) включает в цифровой поток от АЦП дополнительные символы, предназначенные для повышения помехоустойчивости системы связи; 4 – формирователь модулирующих сигналов (ФМС) служит для получения модулирующих сигналов I(t) и Q(t), соответствующих заданному виду модуляции; 5 – сглаживающие формирующие фильтры (СФФ1, СФФ2) необходимы для оптимизации ЦСС в отношении межсимвольной помехи; 6 – перемножители, используются для получения БМ сигналов: синфазного I(t)cosωсt и квадратурного Q(t)sinωсt; 7 – фазовращатель на угол φ = 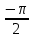 модулятора служит для получения второго несущего колебания, ортогонального по отношению к первому; модулятора служит для получения второго несущего колебания, ортогонального по отношению к первому;8 – генератор гармонических колебаний предназначен для получения несущего колебания; 9 – инвертор изменяет знак перед сигналом; 10 – сумматор модулятора нужен для объединения синфазного и квадратурного сигналов в единый сигнал с квадратурной модуляцией SКАМ(t) = I(t)cosωсt + Q(t)sinωсt; 11 – непрерывный канал является средой распространения сигнала SКАМ(t); 12 – демодулятор (ДМ) нужен для анализа приходящего сигнала, искаженного помехами, и принятии решения о переданном сообщении; 13 – преобразователь параллельного кода в последовательный код служит для преобразования сигнала с выхода демодулятора в последовательный формат кодовых комбинаций; 14 – декодер (ДК) предназначен для исправления части ошибок, возникших при приёме сообщений вследствие влияния помех; 15 – цифро-аналоговый преобразователь (ЦАП) предназначен для восстановления аналоговой формы сигнала по принятым его цифровым отсчётам; 16 – получатель сообщений (ПС). 2. Исходные данныеТаблица 1
3. Расчёт основных характеристик системы передачи цифровой информации3.1. Источник сообщения1. Плотность вероятности мгновенных значений сообщения: 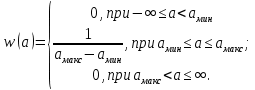 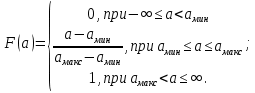 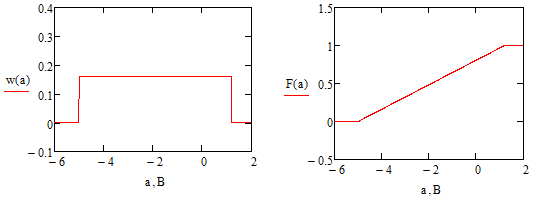 Рис. 1. График плотности вероятности и функции распределения 2. Математическое ожидание сообщения: 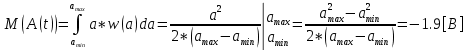 Дисперсия сообщения: 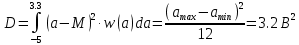 3. Спектральная плотность мощности сообщения:  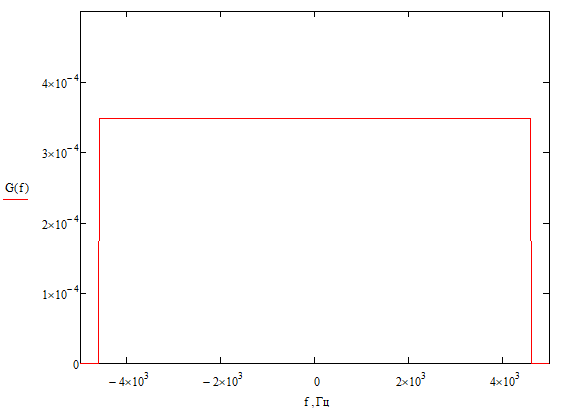 Рис. 3. График спектральной плотности мощности сообщения 4. В соответствии с теоремой Винера-Хинчина корреляционная функция BA(τ)стационарного случайного процесса A(t)определяется по формуле: 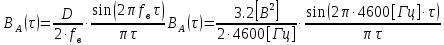 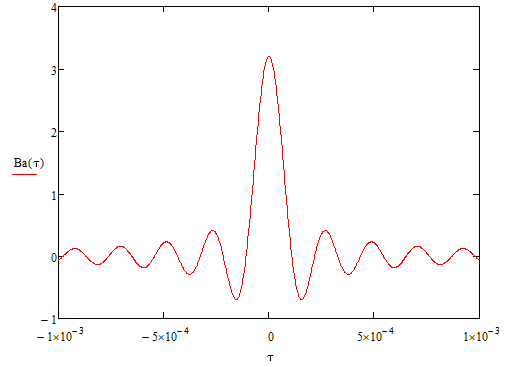 Рис. 4. График корреляционной функции сообщения Как мы видим,  следовательно, сообщение A(t) является эргодическим случайным процессом. следовательно, сообщение A(t) является эргодическим случайным процессом.3.2. Аналого-цифровой преобразователь1. Интервал дискретизации Δt определяется на основе теоремы отсчётов: 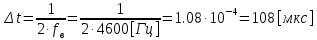 2. Частота дискретизации: 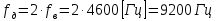 3. Число уровней квантования L:  4. Мощность шума квантования: 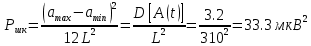  5. Перевод числа 305 в двоичную форму при k = 9: 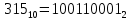 6. Временная осциллограмма отклика АЦП bАЦП(t) на уровень с заданным номером j. Амплитуда U импульсов равна 1 В. 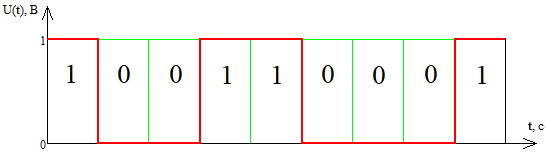 Рис.5. Отклик АЦП на заданный уровень квантования 3.3. Кодер1. Заданы следующие параметры свёрточного кодера: Степень кодирования:  Длина кодового ограничения: 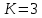 Векторы связи:  2. Структурная схема кодера: 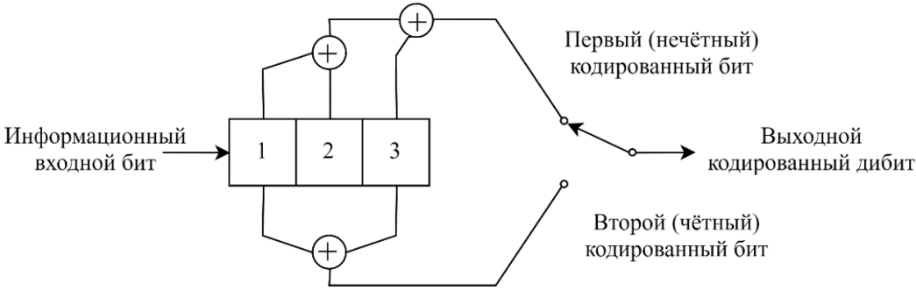 Рис. 6. Структурная схема кодера Решетчатая диаграмма: 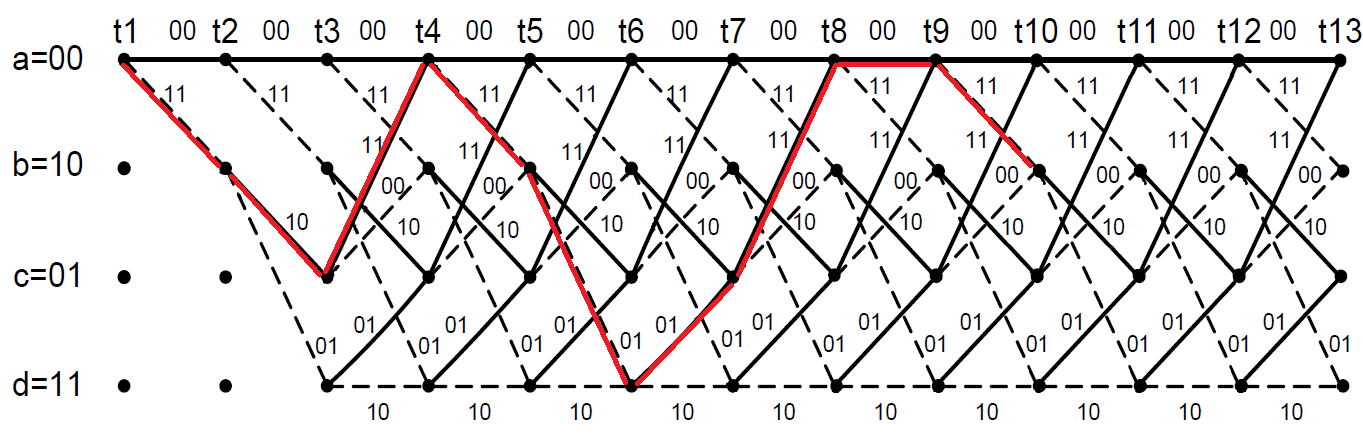 Рис. 7. Решетчатая диаграмма свёрточного кодера от момента времени t1 до момента времени t13 с отмеченным путём, соответствующим полученным КС Заданному уровню квантования j соответствует 1 0 0 1 1 0 0 0 1 двоичная информационная последовательность, поступающая на вход свёрточного кодера (см. табл. 2). Таблица 2
На выходе кодера получена последовательность: «11 10 11 11 01 01 11 00 11» 3.4. Формирователь модулирующих символов1. Сигнальное созвездие КФМ-4: 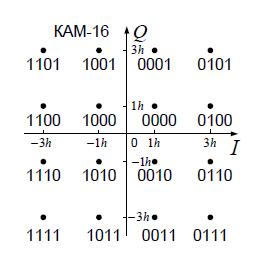 Рис. 8. Сигнальное созвездие квадратурной фазовой модуляции КФМ-4 2. Реализация случайного процесса c(t):  где g1 – прямоугольный импульс длительностью Tв: где g1 – прямоугольный импульс длительностью Tв: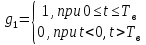 , где , где  Реализации случайных процессов I(t) и Q(t): 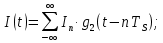 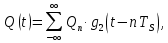 где TS = 4∙TB = 4 ∙ где TS = 4∙TB = 4 ∙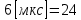 [мкс] [мкс] Рис. 9. а) Реализации c(t) случайного процесса C(t), формируемого с выхода блока свёрточного кодера; б) Реализации с(t) случайного процесса C(t), поступающие на вход блока ФМС; в) Реализации i(t) случайного процесса I(t) на выходе блока ФМС; г)Реализации q(t) случайного процесса Q(t) на выходе блока ФМС 3. Корреляционная функция и спектральная плотность мощность входного случайного процесса C(t):   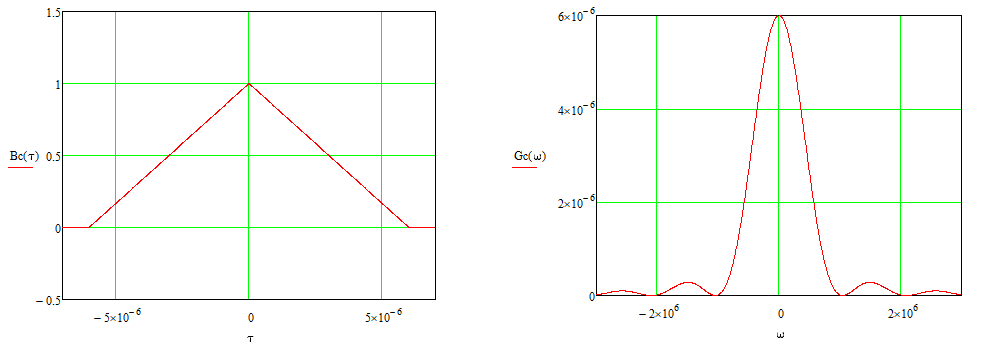 Рис. 10. График корреляционной функции BC(τ) и спектральной плотности мощности GC(ω) случайного процесса C(t) 4. Корреляционные функции и спектральные мощности BI(τ) и BQ(τ):    Рис. 11. График корреляционной функции и спектральной плотности мощности случайных процессов I(t) и Q(t) 5. Сравнение корреляционных функций и спектральных плотностей мощности случайных процессовC(t), I(t) и Q(t): 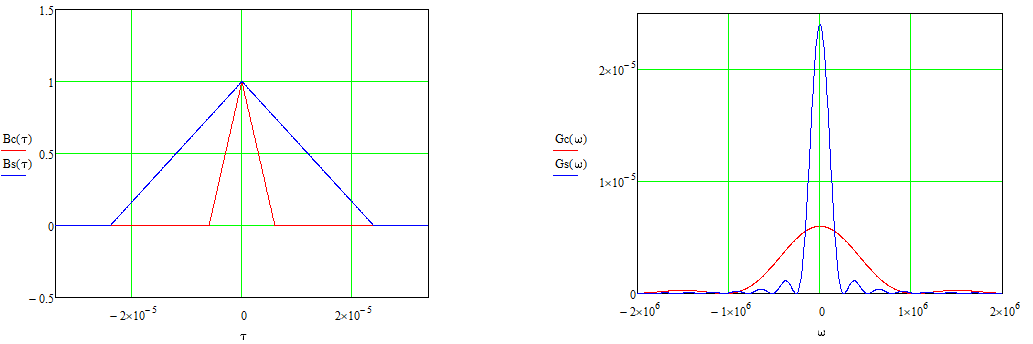 Рис. 12. Сравнение графиков корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС Отличие BI(τ) и BQ(τ) от корреляционной функции BС(τ) проявляется в том, что вместо параметра TB используется параметр TS, где TS – символьный интервал (рис. 14). Форма графика функций GQ(ω) и GI(ω) будет похожа на форму графика GC(ω) на рис.15. Величина главного максимума станет равной TS∙h2, и в точках 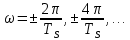 график этих функций будет касаться оси абсцисс ω. график этих функций будет касаться оси абсцисс ω.Для КАМ-4 спектр выходных сигналов уже, так как длительность параллельных импульсов в четыре раза выше, чем последовательного кода, TS = 4∙TB. 3.5. Модулятор3.5.1. Сглаживающий формирующий фильтр1. Структурная схема модулятора  Рис. 13. Структурная схема модулятора в составе ЦСС 2. Импульсы Найквиста x(t) и их спектральные плотности Sx(f)  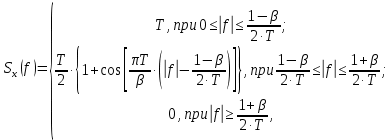 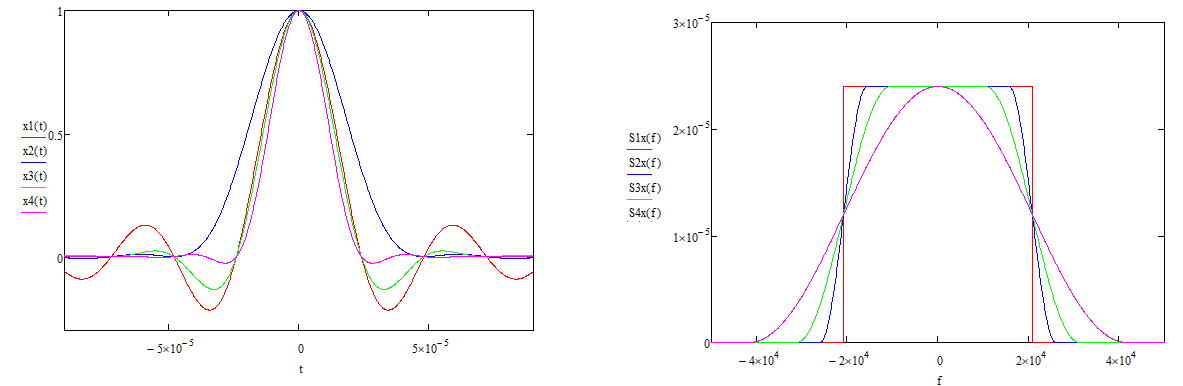 Рис. 14. Импульсы Найквиста x(t) и их спектральные плотности Sx(f) 3. Сравнение спектральных плотностей Sx(ω) и Sx1(ω) сигналов x(t) и x1(t), где x(t) – импульс Найквиста при коэффициенте сглаживания β = 1; x1(t) – импульс со спектральной плотностью  . Максимумы обеих функций находятся в точке 0 и равны . Максимумы обеих функций находятся в точке 0 и равны 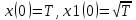 . . Рис. 15. Спектральные плотности Sx(ω) и Sx1(ω) нефинитных импульсов x(t) и x1(t) 4. Сравнение импульсов x(t) и x1(t):  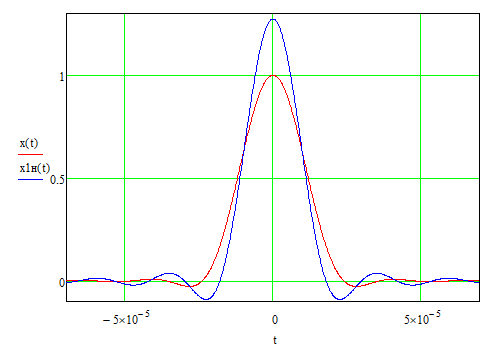 Рис. 16. Импульс Найквиста x(t) и искомый импульс x1(t) Величина главного максимума импульса x(t) равна единице, а величина главного максимума x1(t) зависит от параметра T и равна 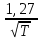 . Нормированный импульс: . Нормированный импульс: 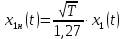 . .5. Аналитические выражения для случайных процессов Iф(t) и Qф(t): На вход СФФ поступает реализация 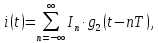 где где 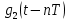 – прямоугольные импульсы. – прямоугольные импульсы.На выходе СФФ получается  где где  имеют форму импульсов x1н(t); имеют форму импульсов x1н(t); 6. Аналитические выражения для корреляционных функций случайных процессов и спектральных плотностей мощности Iф(t) и Qф(t): 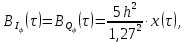 где x(τ) – импульс Найквиста при значении β = 1. где x(τ) – импульс Найквиста при значении β = 1.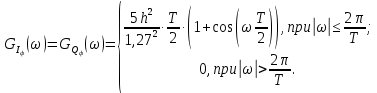  Рис. 17. График корреляционных функций и спектральных плотностей мощности   3.5.2. Блоки перемножителей, инвертор, сумматор1. Аналитические выражения для корреляционных функций 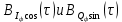 случ. сигналов на выходах перемножителей случ. сигналов на выходах перемножителей где где 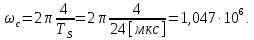 2. Корреляционная функция  сигнала сигнала  на выходе сумматора для КАМ-16 на выходе сумматора для КАМ-16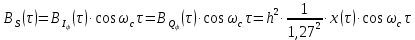  Рис. 18. График корреляционной функции  Спектральная плотность мощности  сигнала сигнала 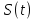 на выходе сумматора для КАМ-16: на выходе сумматора для КАМ-16: 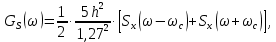 где где 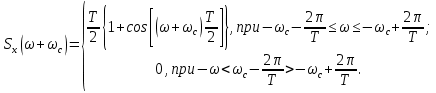  Рис. 19. График спектральной плотности мощности 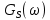 3.6. Непрерывный канал1. Минимальная ширина полосы частот Fk непрерывного канала, необходимая для передачи по каналу сигнала S(t) с выхода модулятора:  2. Средняя мощность информационного сигнала 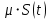 на выходе канала: на выходе канала: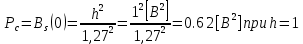 3. Средняя мощность помехи n(t) на выходе канала:   Отношение сигнал/помеха:  4. Пропускная способность C (за секунду) непрерывного канала: 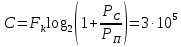 3.7. ДемодуляторСтруктурная схема когерентного демодулятора  Рис. 22. Структурная схема когерентного демодулятора, оптимального по критерию максимального правдоподобия для КАМ-16 Алгоритм работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора: С выхода СФ1 поступает сигнал y(t) = y1(t) + y3(t), где y1(t) – синфазная компонента исходного сигнала, а y3(t) – помеха. Квадратурная компонента y2(t) принимает нулевые значения в моменты времени t = kT. Это свойство является следствием использования квадратурной модуляции.  где T = TS, In – численные значения информационных символов. Далее на обоих входах РУ1 из поступившего сигнала вычитается половина энергии ожидаемого. Если в составе сигнала z(t) сигнал помехи n(t) будет равен нулю, то величина ξ также будет равна нулю и на входе, который соответствует пришедшему сигналу, остаётся максимальное напряжение. Например, для информационного символа I0 = h: 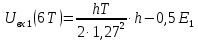 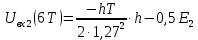  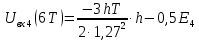 Так как 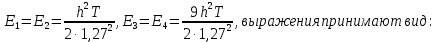   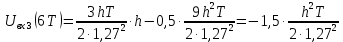 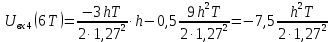 РУ1 принимает решение соответственно входу с максимальным напряжением. Для примера выше (правильный приём) РУ1 примет решение о том, что пришёл информационный символ, соответствующий амплитуде h, т.е. «1». 3. Вероятности ошибок на выходах РУ1 и РУ2 в случае КАМ-16 при значениях символов In и Qn, равных h и – h, когда h = 1 В: 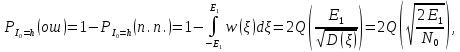 где 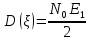 , Q(x) – табулированная функция. , Q(x) – табулированная функция.Вычисляем вероятность ошибки: 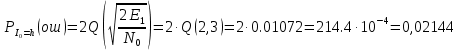  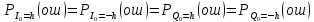  4. Диаграммы сигналов на выходах РУ1, РУ2 и преобразователя кода: Сигнал на выходе РУ1 демодулятора соответствует сигналу i(t) на выходе блока ФМС и поступает на вход преобразователя (см. рис. 24, а). Сигнал на выходе РУ2 демодулятора соответствует сигналу q(t) на выходе блока ФМС и поступает на вход преобразователя (см. рис. 24, б). Сигнал на выходе преобразователя кода преобразован в последовательный из двух параллельных: синфазные компоненты на нечётных отсчётах, квадратурные на чётных. Длительность каждого отсчёта  . Сигнал смещён вправо на величину . Сигнал смещён вправо на величину 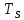 , так как преобразователю кода необходимо принять оба параллельных до того, как он превратит их в последовательный дибит (см. рис.24, в). , так как преобразователю кода необходимо принять оба параллельных до того, как он превратит их в последовательный дибит (см. рис.24, в).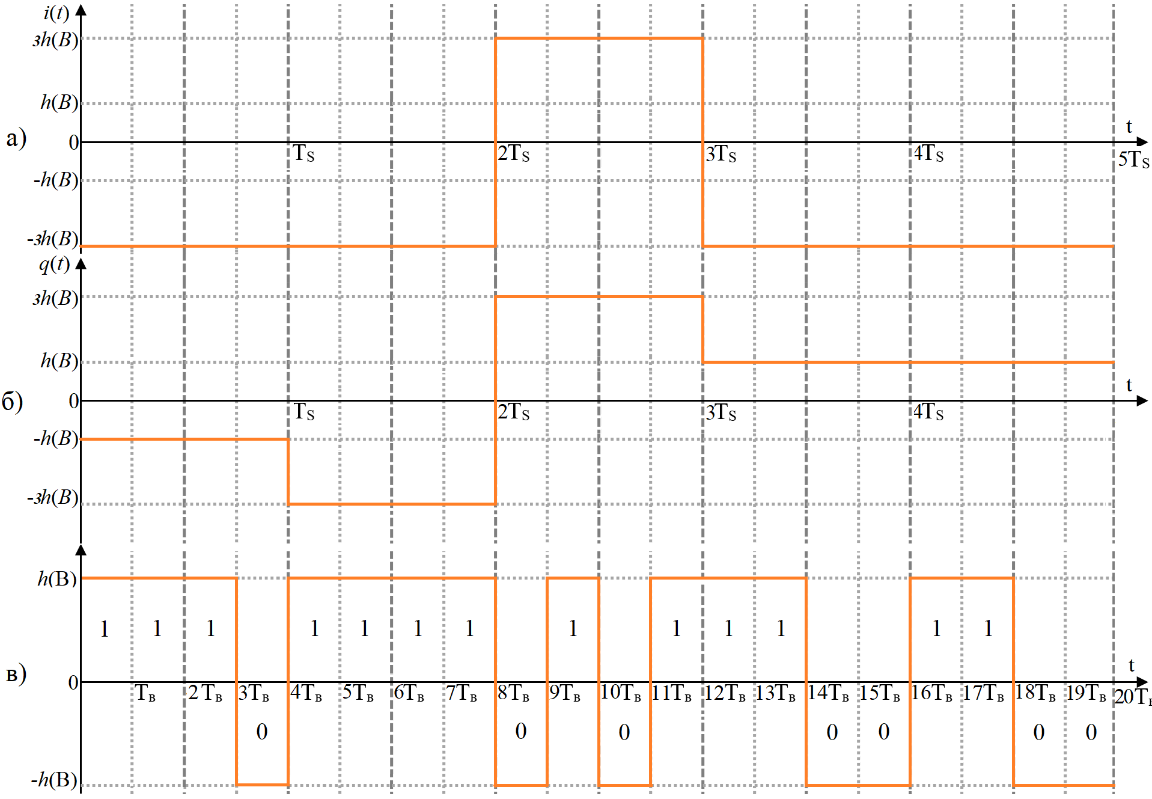 Рис. 24. а) Сигнал на выходе РУ1 демодулятора б) Сигнал на выходе РУ2 демодулятора в) Сигнал на выходе преобразователя кода 5. Вероятность ошибочного приёма на выходе преобразователя параллельного кода в последовательный код: 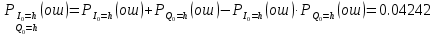  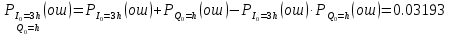 6. Средняя вероятность ошибки: Так как вероятности ошибок для всех четырёх точек сигнального созвездия равны, средняя вероятность ошибки равна вероятности ошибки на любом созвездии:  3.8. ДекодерЧисленные значения кодовых символов на выходе кодера:  После прохождения через демодулятор последовательность 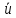 трансформируется в последовательность трансформируется в последовательность 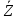 на выходе демодулятора. на выходе демодулятора.В демодуляторе на 6-м тактовом интервале (g = 6) произошла ошибка. Тогда последовательность 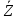 на выходе демодулятора будет равна: на выходе демодулятора будет равна:  Рис. 24 Решетчатая диаграмма декодера последовательности 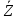 Диаграммы выживших путей от момента времени t1 до момента времени tk+2  Рис. 15 Декодирование с 4 такта по 8  Рис. 26 Декодирование с 9 такта по 12 Как мы видим к t10 идёт 2 пути, но у верхнего пути последний шаг имеют больший вес, чем у нижнего, поэтому мы выбираем нижний путь.  Рис. 27 Перенесённый выживший путь на диаграмму кодера Вывод: в результате декодирования была получена исходная последовательность  . Поэтому можно сказать, что сверточное кодирование способно однозначно исправить ошибку в одном бите. Для декодирования последовательности из 9 символов требуется 12 тактов. . Поэтому можно сказать, что сверточное кодирование способно однозначно исправить ошибку в одном бите. Для декодирования последовательности из 9 символов требуется 12 тактов.ЗАКЛЮЧЕНИЕ В ходе выполнения курсовой работы были изучены принципы работы цифровой системы связи. Были вычислены математическое ожидание, дисперсия, определена спектральная плотность мощности и корреляционная функция источника сообщения. Были рассчитаны параметры АЦП и определен сигнал на выходе АЦП для заданного во варианте номере квантования. Был рассмотрен модулятор КФМ-4, рассчитаны его основные характеристики: корреляционная функция и спектральная плотность мощность для сигналов на входе и выходе модулятора. Были рассмотрены сигналы Найквиста, позволяющие устранить межсимвольную и межканальную интерференцию. Были рассмотрены непрерывный канал и демодулятор, определены характеристики непрерывного канала и алгоритм работы демодулятора. Были рассчитаны вероятности ошибок при демодуляции. Был рассмотрен алгоритм декодирования Витерби, произведено декодирование последовательности с одной допущенной ошибкой, исправленной в результате декодирования. Список литературы 1. Куликов, Л. Н. Общая теория связи: методические указания к выполнению курсовой работы / Л.Н. Куликов, М.Н. Москалец, П.П. Шумаков. – СПб. : СПбГУТ, 2016. 2. Биккенин, Р. Р. Теория электрической связи : учеб. пособие / Р.Р.Биккенин, М.Н.Чесноков. – Л. : ЛЭИС, 2010. 3. Сальников, А.П. Теория электрической связи : конспект лекций / А.П. Сальников. –СПб. : Линк, 2007. | |||||||||||||||||||||||||||||||||||||||||||||||

