Курсовая по математическому программированию. Пояснительная записка Муравьев. Курсовая работа вариант 14 Рекуррентные соотношения и динамическое программирование Муравьев В. В
 Скачать 106.04 Kb. Скачать 106.04 Kb.
|
|
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта Федеральное государственное бюджетное образовательное учреждение высшего образования «Дальневосточный государственный университет путей сообщения» (ДВГУПС) Кафедра «Информационные технологии и системы» Направление подготовки (специальности) 09.03.02 Информационные системы и технологии Дисциплина «Математическое программирование» КУРСОВАЯ РАБОТА Вариант 14 Рекуррентные соотношения и динамическое программирование Выполнил: Муравьев В.В. гр. БО231ИСТ Проверил: Карачанская Е.В. Хабаровск 2021 СодержаниеСодержание 2 Задание на курсовую работу 3 Введение 4 Общая постановка задачи динамического программирования и ее решение. 5 Рекуррентные соотношения. Числа Фибоначчи 8 Программная реализация решения поставленной задачи методом ДП. 10 Заключение 15 Список использованной литературы 16 Задание на курсовую работу«Динамическое программирование» по дисциплине «Математическое программирование» Студент Муравьев Вячеслав Валерьевич БО231ИСТ группы. Тема «Рекуррентные соотношения и динамическое программирование» Дата выдачи задания: 24 февраля 2021 года Срок сдачи: до 1 мая 2021 года – досрочно до 15 мая 2021 года – в срок. Задание на разработку: Изучить постановку задачи динамического программирования (ДП) и ее решение. Составление уравнений Бэллмана. В соответствии с вариантом решить задачу методом ДП (с составлением уравнений Бэллмана) Разработать программный продукт, решающий данный тип задач методом ДП с краткой инструкцией по его использованию. Пояснительная записка должна включать следующие основные разделы: Содержание. Текст задания (этот бланк). Введение (актуальность, цель, задачи) Общая постановка задачи динамического программирования и ее решение. Формулировка конкретной (в соответствии с вариантом) задачи, сведение ее к задаче динамического программирования, ее решение методом ДП. Программная реализация решения поставленной задачи методом ДП. Заключение. Список использованной литературы Компакт-диск с текстом пояснительной записки в формате MS Word и программный продукт с инструкцией пользователя. Рекомендуемая литература. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования.—М.: Наука, 1965.— 458 с. Окулов С.М., Пестов О.А. Динамическое. программирование. 2-е издание (электронное). Москва БИНОМ. Лаборатория знаний 2015. Лежнев А.В. Динамическое программирование в экономических задачах . - М.: Бином. Лаборатория знани . 2010 . - 176 с. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы_ построение и анализ. 2-е издание. Издательство: Вильямс,. - 2005. - 1293 c. Задание выдал доцент кафедры «Информационные технологии и системы» Карачанская Е.В. 24.02.2021 ВведениеБольшу́ю часть математических задач представляют задачи, требующие нахождения оптимального решения, выбора наилучшего варианта среди множества других, а также принятия рациональных решений. Данный тип задач требует перебора большого количества различных вариантов, что, во-первых, является трудоёмким процессом и занимает много времени, а во-вторых, повышает вероятность допущения ошибок. Метод динамического программирования является одним из наиболее мощных методов оптимизации, использующихся для решения вышеперечисленных задач. Его основной принцип заключается в разделении основной, более трудной задачи на множество мелких, решение которых представляется менее трудоёмким. В данной работе будет рассматриваться задача о рекуррентных соотношениях, а именно – задача о числах Фибоначчи. В основном последовательность Фибоначчи используется в анализе финансовых, товарных и иных рынков, прогнозировании трендовых товаров (волновая теория Эллиота) и архитектуре (золотое сечение). Целью данной работы является разработка программного продукта, позволяющего найти значение искомого элемента последовательности Фибоначчи по его номеру. Задачи курсовой работы: Изучить постановку задачи динамического программирования; Изучить постановку задачи о числах Фибоначчи; Решить конкретную задачу методом динамического программирования и составить уравнения Бэллмана; Разработать программный продукт, решающий данный тип задач методом динамического программирования; Составить краткое руководство пользователя к разработанной программе. Общая постановка задачи динамического программирования и ее решение.Пусть имеется некоторая физическая система  , которая с течением времени меняет свое состояние, т. е. в системе , которая с течением времени меняет свое состояние, т. е. в системе  происходит какой-то процесс. Мы можем управлять этим процессом, т. е. тем или другим способом влиять на состояние системы за происходит какой-то процесс. Мы можем управлять этим процессом, т. е. тем или другим способом влиять на состояние системы за  шагов. Такую систему шагов. Такую систему  мы будем называть управляемой системой, а способ нашего воздействия на нее — управлением мы будем называть управляемой системой, а способ нашего воздействия на нее — управлением . .На каждом шаге необходимо определить два типа переменных: переменную состояния системы  и переменную управления и переменную управления  . Переменная . Переменная  определяет, в каких состояниях может оказаться система на рассматриваемом определяет, в каких состояниях может оказаться система на рассматриваемом 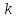 -ом шаге, а переменная -ом шаге, а переменная 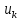 есть управление, переводящее систему из начального состояния есть управление, переводящее систему из начального состояния 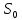 в состояние в состояние 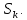 Тогда последовательность состояний системы можно представить в виде графа (рис. Рисунок 1). Тогда последовательность состояний системы можно представить в виде графа (рис. Рисунок 1). Рисунок 1 – Граф состояний системы уравнений Предположим, что с процессом связана какая-то наша заинтересованность, выражающаяся целевой функцией  , которая называется «выигрыш». Данная функция зависит от начального состояния и управления , которая называется «выигрыш». Данная функция зависит от начального состояния и управления и является аддитивной, т.е. складывается из полученных решений  Состояние системы  на каждом шаге зависит от предшествующего состояния на каждом шаге зависит от предшествующего состояния  и этого управляющего воздействия и этого управляющего воздействия  и может быть записано в виде: и может быть записано в виде: Задача динамического программирования заключается в нахождении такого оптимального управления  , при котором значение целевой функции (выигрыш) будет максимально. , при котором значение целевой функции (выигрыш) будет максимально.При решении задачи динамического программирования используют принцип оптимальности Бэллмана: Каково бы ни было состояние  системы в результате системы в результате  числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный. числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.Т.е. решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем,  -ом шаге. -ом шаге.Математической формулировкой данного принципа являются функциональные уравнения Бэллмана, выглядящие следующим образом:  Общая схема решения задач динамического программирования: Выбрать способ деления процесса управления на шаги; Определить параметры состояния  и переменные управления и переменные управления  на каждом шаге; на каждом шаге;Записать уравнения состояний; Ввести целевую функцию  -ого шага и суммарную целевую функцию; -ого шага и суммарную целевую функцию;Ввести в рассмотрение условные максимумы (минимумы)  и условное оптимальное управление на и условное оптимальное управление на  -ом шаге: -ом шаге:  ; ;Записать основные для вычислительной схемы динамического программирования уравнения Беллмана для  и и  ; ;Последовательно решить уравнения Беллмана; Результатом выполнения условной оптимизации является оптимальное решение для конкретного начального состояния  : :  Рекуррентные соотношения. Числа ФибоначчиГоворят, что последовательность  задана рекуррентно, если существует формула, выражающая задана рекуррентно, если существует формула, выражающая  -й член этой последовательности через один или несколько предыдущих членов; такая формула называется рекуррентным соотношением. -й член этой последовательности через один или несколько предыдущих членов; такая формула называется рекуррентным соотношением.Примером рекуррентного соотношения являются числа Фибоначчи. Числа Фибоначчи – последовательность чисел, в которой первые два числа равны 0 и 1, а каждое последующее число равно суме двух предыдущих. Более формально последовательность чисел Фибоначчи задаётся линейным рекуррентным соотношением:  , где , где  Формулировка задачи: по заданному номеру элемента  вычислить его значение вычислить его значение  Сведение к задаче динамического программирования. Очевидно, что данная задача имеет рекурсивное решение благодаря рекуррентной записи для вычисления элемента. Простое рекурсивное решение неэффективно, т.к. приходится многократно вычислять одни и те же значения элементов ряда. Например, из формул 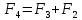 и и 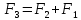 следует, что для вычисления следует, что для вычисления 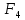 значение значение 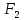 приходится вычислять дважды. приходится вычислять дважды.Сведём задачу к задаче динамического программирования. Пусть исходная задача T - это вычисление 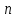 -го элемента ряда Фибоначчи. В качестве последовательности подзадач -го элемента ряда Фибоначчи. В качестве последовательности подзадач 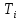 выберем последовательность задач выберем последовательность задач 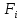 , которые сводятся к вычислению , которые сводятся к вычислению 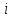 -го члена ряда. Тогда -го члена ряда. Тогда  и и  нам известны ( нам известны ( ), а ), а  - это как раз поставленная выше задача. Каждая задача - это как раз поставленная выше задача. Каждая задача  легко может решаться через предшествующие ей задачи: легко может решаться через предшествующие ей задачи:  = =  + +  (для (для  ). Поэтому последовательно вычисляя значение ). Поэтому последовательно вычисляя значение  мы линейным алгоритмом найдем и последний искомый элемент мы линейным алгоритмом найдем и последний искомый элемент  . .Составим уравнение Бэллмана:  Решение конкретной задачи методом динамического программирования. Пусть  При помощи составленного выше уравнения Бэллмана решим задачу:    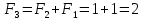 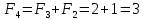 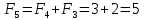 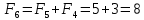  Вместо того, чтобы на каждом шаге заново вычислять элементы последовательности, мы используем уже полученные на предыдущих шагах данные, уменьшая тем самым время, затрачиваемое на решение задачи. Программная реализация решения поставленной задачи методом ДП.Код программы. Метод F, вычисляющий последовательность Фибоначчи: public ulong[] F(int n) { ulong[] fibonacci = new ulong[n+1]; for (int i = 0; i < fibonacci.Length; i++) { if (i == 0) //Если n=0 { fibonacci[i] = 0; textBoxProcess.Text = textBoxProcess.Text + $"F({i}) = {fibonacci[i]}" + '\r' + '\n'; } else if (i == 1) //Если n=1 { fibonacci[i] = 1; textBoxProcess.Text = textBoxProcess.Text + $"F({i}) = {fibonacci[i]}" + '\r' + '\n'; } else //Если n≥2 { fibonacci[i] = fibonacci[i - 1] + fibonacci[i - 2]; textBoxProcess.Text = textBoxProcess.Text + $"F({i}) = {fibonacci[i]}" + '\r' + '\n'; } } return fibonacci; } Согласно выше определённому уравнению Бэллмана, данный метод вычисляет и возвращает массив элементов последовательности Фибоначчи. Его входным параметром является номер искомого элемента  . Кроме вычисления последовательности на каждом шаге заполняется поле textboxProcess, показывающее ход решения задачи. . Кроме вычисления последовательности на каждом шаге заполняется поле textboxProcess, показывающее ход решения задачи.Нажатиекнопки «Вычислить»: if (int.TryParse(textBoxInput.Text, out int n) == false) MessageBox.Show("Неправильно заполнено поле с номером элемента! N - положительное натуральное число", "Ошибка!", MessageBoxButtons.OK, MessageBoxIcon.Error); else if (Convert.ToInt32(textBoxInput.Text) < 0) MessageBox.Show("Номер элемента не может быть отрицательным! Введите правильное значение", "Ошибка!", MessageBoxButtons.OK, MessageBoxIcon.Error); else textBoxOutput.Text = F(Convert.ToInt32(textBoxInput.Text))[Convert.ToInt32(textBoxInput.Text)].ToString(); После нажатия кнопки происходит проверка данных, введённых пользователем. Не должно быть так, что пользователь ввёл: ненатуральное число, символы алфавита и т.д.; отрицательное число. Если введённые данные соответствуют представленным условиям, то происходит вычисление последовательности Фибоначчи. Событие «Изменение значения поля textBoxInput» textBoxProcess.Clear(); textBoxOutput.Clear(); При изменении значения номера элемента последовательности  происходит очищение результирующих полей. происходит очищение результирующих полей.Нажатие Enterв поле ввода номера элемента if (e.KeyCode == Keys.Enter) { buttonGO.PerformClick(); } Нажатие Enter выполняет те же функции, что и кнопка «Вычислить». Руководство пользователя Программный продукт, решающий поставленную задачу методом динамического программирования, был написан на языке программирования C# при помощи программного продукта Visual Studio и технологии Windows Forms. Программа состоит из одной главной формы (Рис. Рисунок 2), в которой находятся: - поле для ввода номера искомого элемента  ; ;- поле, в котором выводятся вычисления значений предыдущих элементов; - поле, в котором выводится значение искомого элемента  ; ;- кнопка «Вычислить», запускающая вычислительный процесс.  Рисунок 2 – Главная форма приложения Для начала работы необходимо ввести номер элемента последовательности Фибоначчи  , значение которого требуется вычислить, в поле (1). Другие поля являются неактивными. , значение которого требуется вычислить, в поле (1). Другие поля являются неактивными.Начать вычисление можно двумя способами: нажать кнопку «Enter» на клавиатуре, нажать кнопку (4) «Вычислить». После нажатия поля (3) и (4) будут автоматически заполнены. В поле (3) представлен ход решения задачи. Здесь можно увидеть значения всех предыдущих элементов. В поле (4) же можно увидеть значение искомого элемента. Пример работы приложения:  Рисунок 3 – Пример работы приложения При работе с приложением могут возникнуть следующие ошибки: 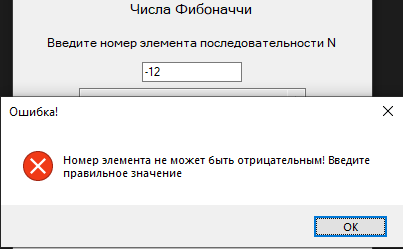 Данная ошибка появляется, когда пользователь в качестве номера элемента 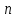 вводит отрицательное число. Для её решения необходимо исправить значение на положительное. вводит отрицательное число. Для её решения необходимо исправить значение на положительное.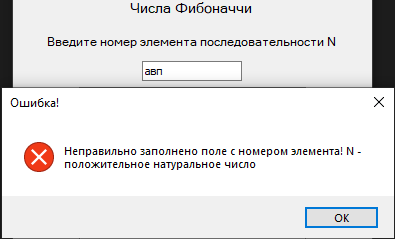 ИЛИ 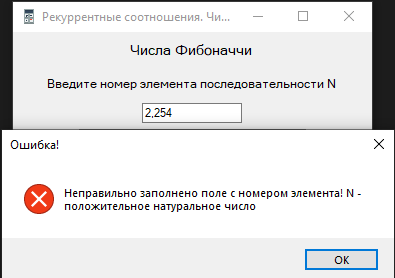 Данная ошибка появляется, когда пользователь в качестве номера элемента 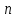 вводит либо символы, не являющиеся числом, либо ненатуральные числа. Для её решения необходимо исправить значение вводит либо символы, не являющиеся числом, либо ненатуральные числа. Для её решения необходимо исправить значение 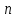 на положительное натуральное число. на положительное натуральное число.ЗаключениеВ ходе данной работы был изучен метод оптимизации «Динамическое программирование», постановка его задачи и способ практического применения. После чего данным способом была решена задача на рекуррентные соотношения. Конкретная задача, а именно задача на числа Фибоначчи, была сведена к задаче динамического программирования. После чего было составлено уравнение Бэллмана, на основе которого был разработан программный продукт, позволяющий решить данный вид задачи автоматически. Список использованной литературыВентцель Е. С. Исследование операций. 1972г. 552 с Новиков А.И. Экономико-математические методы и модели. 2017 Окулов С.М., Пестов О.А. Динамическое. программирование. 2-е издание (электронное). Москва БИНОМ. Лаборатория знаний 2015. Интернет-ресурс «Школа программиста». Статья «Динамическое программирование. Числа Фибоначчи» - URL: https://acmp.ru/article.asp?id_sec=1&id_text=1331 |
