Курсовая по механике. Курсовая. Курсоваяработ а по разделу Динамика Исследование колебаний механической системы с одной степенью свободы
 Скачать 237.48 Kb. Скачать 237.48 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра теоретической механики К У Р С О В А Я Р А Б О Т А по разделу «Динамика» «Исследование колебаний механической системы с одной степенью свободы» Вариант № 4 Т У Л А 2022 Оглавление Введение…………………………………………………………………………...3 1. Построение расчетной схемы………………………………………………...5 2. Составление дифференциального уравнения движения механизма…...6 3. Решение дифференциального уравнения движения механизма……….12 4. Определение реакций внешних и внутренних связей…………………...15 Литература……………………………………………………………………….18 Введение Задача заключается в исследовании движения механизма с одной степенью свободы, изображенного на рис. 1. Определить реакции внешних и внутренних связей. Массами нитей и упругих элементов пренебречь. Нити считать нерастяжимыми и абсолютно гибкими. В качестве координаты, определяющей положение системы, принять перемещение груза 1 – S. Качение катка 3 происходит без скольжения. К грузу 1 приложена возмущающая сила F(t). 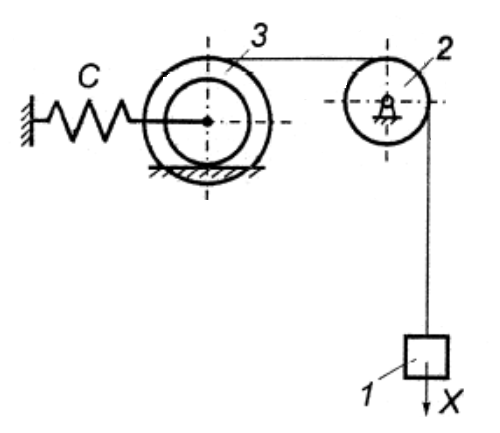 Рис. 1 Данные для вычислений принять следующие: 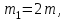 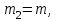 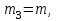 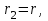 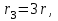 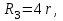 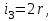 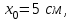 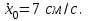 Содержание работы Дана механическая система, представляющая собой совокупность абсолютно твердых тел, связанных друг с другом посредством нерастяжимых нитей. Система снабжена упругой внешней связью с жесткостью С. Заданы инерционные и геометрические характеристики тел механической системы. Требуется исследовать динамическое поведение механической системы, Определить реакции внешних и внутренних связей. Трением скольжения и качения пренебречь. В расчетах принять следующие данные: 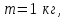 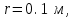 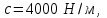 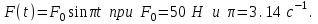 Построение расчетной схемы Расчетная схема изображенного на рис. 1 механизма образуется на основе его освобождения от несущественных связей путем замещения их соответствующими реакциями в силу известного принципа освобождаемости связей. Образованная таким образом расчетная схема представлена на рис. 2. 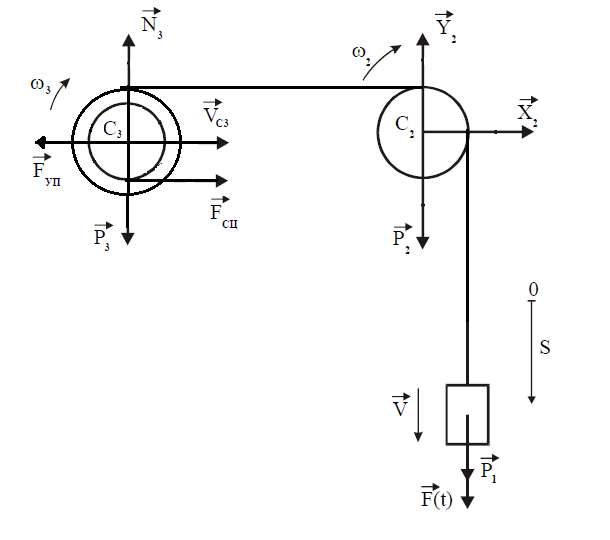 Рис. 2 Составление дифференциального уравнения движения механизма Поскольку рассматриваемая механическая система обладает одной степенью подвижности, положения ее звеньев будут однозначно определяться координатой S. Следовательно, эта координата будет выступать в качестве обобщенной координаты в процессе математического описания движения исследуемой системы. Для составления дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в виде 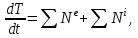 (2.1) (2.1)где 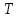 – кинетическая энергия системы; – кинетическая энергия системы;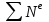 – сумма мощностей внешних сил; – сумма мощностей внешних сил;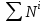 – сумма мощностей внутренних сил. – сумма мощностей внутренних сил.Кинетическая энергия системы, показанной на рис. 2, слагается из кинетических энергий трех, составляющих механическую систему тел, т.е. 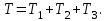 (2.2) (2.2)Груз 1 совершает поступательное движение. Его кинетическая энергия равна: 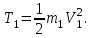 (2.3) (2.3)Блок 2 совершает вращательное движение. Его кинетическая энергия равна: 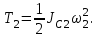 (2.4) (2.4)И наконец, каток 3 совершает плоскопараллельное движение. Его кинетическая энергия равна: 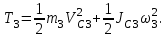 (2.5) (2.5)Кинетическая энергия всего механизма будет равна: 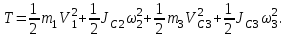 (2.6) (2.6)Выразим 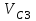 , , 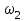 и и 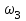 через скорость груза через скорость груза 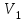 . Получим: . Получим: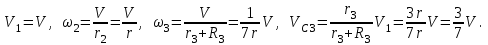 (2.7) (2.7)Подставляя зависимости (2.7) в выражение (2.6), получим: 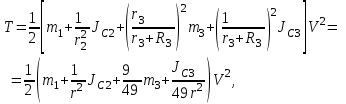 (2.8) (2.8)где последнее выражение в скобках представляет собой приведенную массу механической системы, а именно: 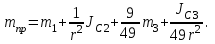 (2.9) (2.9)С учетом приведенной массы механической системы (2.9) выражение для кинетической энергии системы принимает следующий вид: 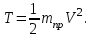 (2.10) (2.10)Производная функции кинетической энергии повремени равна: 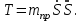 (2.11) (2.11)Теперь переходим к вычислению правой части уравнения (2.1). Как известно, мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения: 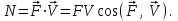 (2.12) (2.12)Рассматриваемая механическая система является неизменяемой, т.е. тела, входящие в систему, не деформируемы, и скорости их точек друг относительно друга равны нулю. Поэтому сумма мощностей внутренних сил будет равна нулю: 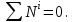 (2.13) (2.13)Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, такими силами являются: 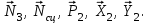 Сумма мощностей остальных сил определяется: 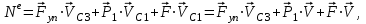 (2.14) (2.14)или, раскрывая скалярные произведения, будем иметь 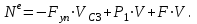 (2.15) (2.15)С учетом кинематических соотношений (2.7) сумму мощностей внешних сил преобразуем к виду 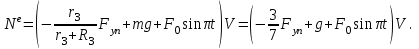 (2.16) (2.16)Выражение для суммарной мощности внешних сил запишем в форме: 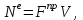 (2.17) (2.17)где 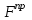 – приведенная сила, которая равна – приведенная сила, которая равна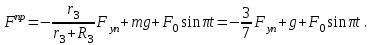 (2.18) (2.18)Преобразуем выражение (2.18). Упругую силу будем считать пропорциональной удлинению пружины. Полное удлинение пружины f равно сумме статического 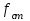 и динамического и динамического 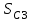 удлинений, т.е. удлинений, т.е. причем из выражений (2.7) для  следует, что следует, что  Тогда упругая сила будет равна:  (2.19) (2.19)С учетом (2.19) выражение для приведенной силы (2.18) можно записать: 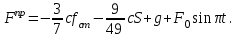 (2.20) (2.20)В состоянии покоя, т.е. при 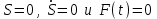 , приведенная сила должна быть равна нулю. Получаем условие равновесия системы: , приведенная сила должна быть равна нулю. Получаем условие равновесия системы: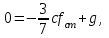 (2.21) (2.21)откуда заключаем, что 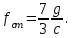 (2.22) (2.22)После подстановки (2.22) в (2.20) получим: 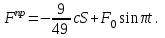 (2.23) (2.23)Подставляем выражение для производной от кинетической энергии (2.11) и сумму мощностей всех сил (2.17) с учетом (2.23) в уравнение (2.1). Тогда получаем дифференциальное уравнение движение механической системы: 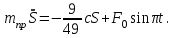 (2.24) (2.24)Запишем дифференциальное уравнение (2.24) в виде: 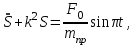 (2.25) (2.25)где 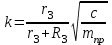 – циклическая частота свободных колебаний. – циклическая частота свободных колебаний.Запишем начальные условия движения: 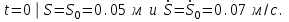 (2.26) (2.26)Дифференциальное уравнение (2.25) совместно с начальными условиями (2.26) представляют собой математическую модель заданной механической системы в связи с решением второй задачи динамики. Решение дифференциального уравнения движения механизма Общее решение S неоднородного дифференциального уравнения (2.25) складывается из общего решения однородного 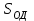 и частного решения и частного решения 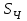 неоднородного, т.е. неоднородного, т.е. 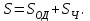 Однородное дифференциальное уравнение, соответствующее данному неоднородному дифференциальному уравнению, имеет вид: 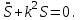 (3.1) (3.1)Решение этого уравнения ищем в виде функции: 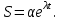 (3.2) (3.2)Подставляя (3.2) в (3.1), получим: 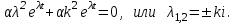 (3.3) (3.3)Поскольку корни характеристического уравнения комплексно-сопряженные, то общее решение дифференциального уравнения (3.1) принимает вид: 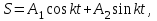 (3.4) (3.4)где 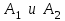 – произвольные постоянные интегрирования, подлежащие отысканию из начальных условий. – произвольные постоянные интегрирования, подлежащие отысканию из начальных условий.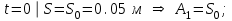 (3.5) (3.5)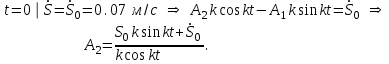 (3.6) (3.6)После подстановки (3.5) и (3.6) в (3.4) получим: 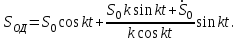 (3.7) (3.7)Определяем частное решение неоднородного дифференциального уравнения: 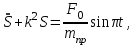 (3.8) (3.8)Частное решение неоднородного дифференциального уравнения (3.8) ищем в виде правой части (3.8): 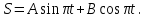 (3.9) (3.9)Подставляя (3.9) в (3.8) будем иметь: 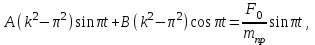 (3.10) (3.10)откуда вытекают два алгебраических уравнения относительно произвольных постоянных А и В 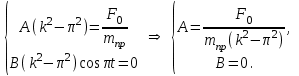 (3.11) (3.11)Следовательно, частное решение неоднородного дифференциального уравнения (3.8) принимает окончательный вид: 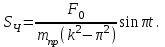 (3.12) (3.12)Складывая решения (3.7) и (3.12), получаем общее решение дифференциального уравнения (2.25): 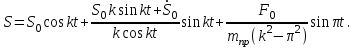 (3.13) (3.13)Полученная зависимость обобщенной координаты S от времени выражает закон движения заданной механической системы. Определение реакций внешних и внутренних связей Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис. 3). 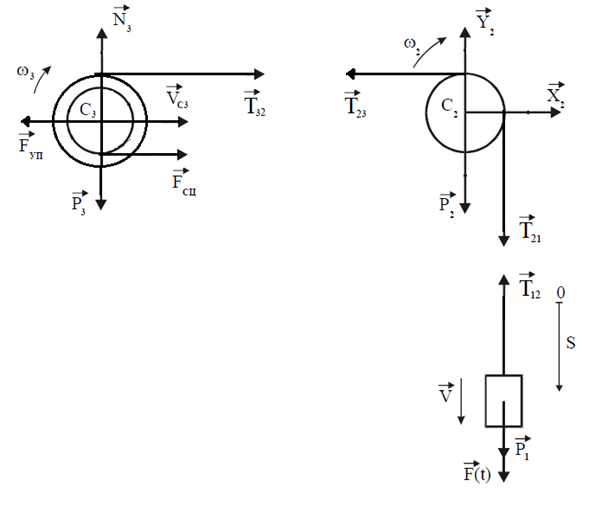 Рис. 3 Определение реакций связей проводим с помощью теоремы об изменении количества движения и теоремы об изменении кинетического момента относительно центра масс. Так, для катка 3 будем иметь: 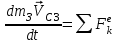 (4.1) (4.1)и 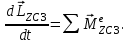 (4.2) (4.2)В соответствии с расчетными схемами на рис. 3 записываем уравнения (4.1) и (4.2) в проекциях на оси координат. Тело 1 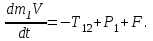 (4.3) (4.3)Тело 2 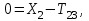 (4.4) (4.4)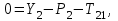 (4.5) (4.5)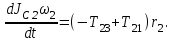 (4.6) (4.6)Тело 3 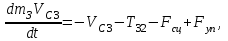 (4.7) (4.7)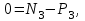 (4.8) (4.8)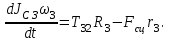 (4.9) (4.9)С учетом кинематических соотношений (2.7) система уравнений (4.3) – (4.9) приводится к виду: 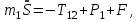 (4.10) (4.10)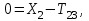 (4.11) (4.11)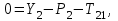 (4.12) (4.12)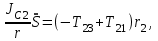 (4.13) (4.13)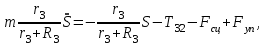 (4.15) (4.15)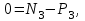 (4.16) (4.16)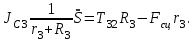 (4.17) (4.17)Уравнения (4.10) – (4.17) составляют систему алгебраических уравнений относительно функций: 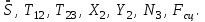 Разрешая систему уравнений (4.10) – (4.17) относительно перечисленных неизвестных, получаем дифференциальное уравнение движение материальной системы и выражения для определения неизвестных реакций связей. Литература: 1. Методические указания. 2. Конспекты лекций по разделу " Динамика ". 3. Никитин Н.Н. Курс теоретической механики. - М.: Высшая школа, 1990. – 607 с. 4. Яблонский А.А. Курс теоретической механики. Т.2. - М.: Высшая школа, 1984. - 424 с. 5. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т.2. – М.: Наука, 1979. – 544 с. 5. Тарг С.М. Краткий курс теоретической механики. - М.: Наука, 1988. - 482 с. |
