Исследование плоскорычажного механизма 1 Структурный анализ механизма
 Скачать 296.29 Kb. Скачать 296.29 Kb.
|
|
Содержание 1. Структурное и кинематическое исследование плоско-рычажного механизма 1.1 Структурный анализ механизма 1.2 Кинематический анализ механизма 2. Силовой анализ плоско-рычажного механизма 2.1 Определение внешних сил 2.2 Определение внутренних сил 3. Синтез зубчатого механизма 3.1 Геометрический синтез зубчатого зацепления 3.2 Определение размеров внешнего зубчатого зацепления 1. Структурное и кинематическое исследование плоско-рычажного механизма 1.1 Структурный анализ механизма Наименование звеньев и их количество Дана структурная схема механизма. Механизм предназначен для преобразования вращательного движения кривошипа 1 в возвратно-поступательное движение ползуна 5. Для данного кривошипно-ползунного механизма (изображенного на 1 листе графического задания), наименование звеньев и их количество приведено в таблице 1. Таблица 1 - Наименование звеньев и их количество
Всего звеньев 6 из них подвижных n=5 Кинематические пары и их классификации Для данного кривошипно-ползунного механизма кинематические пары и их классификации приведены в таблице 2. Таблица 2 - Кинематические пары и их классификации
Всего звеньев 6 из них подвижных n=5 Степень подвижности механизма Число степеней свободы (степень подвижности) кривошипно-ползунного механизма определяется по формуле П.Л. Чебышева: 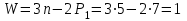 где n – число подвижных звеньев механизма; P1 – число одноподвижных кинематических пар. Т.к. W=1 механизм имеет одно ведущее звено и это звено №1. Разложение механизма на структурные группы (группы Ассура) Проведенное разложение кривошипно-ползунного механизма на структурные группы (группы Ассура) приведено в таблице 3. Таблица 3 - Разложение механизма на структурные группы (группы Ассура)
Структурная формула механизма (порядок сборки) 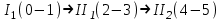 К механизму 1 класса, 1 вида состоящего из звеньев 0 и 1 присоединена группа Ассура II класса, 2 порядка, 1 модификации состоящая из звеньев 2 и 3. К этой группе присоединена группа Ассура II класса, 2 порядка, 2 модификации состоящая из звеньев 4 и 5. 1.2 Кинематический анализ механизма Цель: определение положения звеньев и траектории движения их точек, определение скоростей и ускорений точек звеньев, а также определение угловых скоростей и угловых ускорений звеньев по заданному закону движения ведущего звена. Графический метод кинематического анализа Заключается в построении графиков перемещении, скорости и ускорения последнего звена механизма в функции от времени (построение кинематических диаграмм) и определение их истинных значений. Построение планов положения механизма Кинематический анализ начинаем с построения плана положения механизма. Для этого должны быть известны: 1) размеры звеньев механизма, м; 2) величина и направление угловой скорости ведущего звена 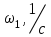 . .Размеры звеньев механизма равны: 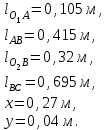 Выбираем масштабный коэффициент длины: 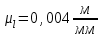 Нулевым положением является крайнее левое положение ползуна 5 – начало преодоления силы F п.с. Построенный план положения механизма представлен на листе №1 графической части курсового проекта. Длина отрезков, изображающих звенья механизма на чертеже, будут равны: 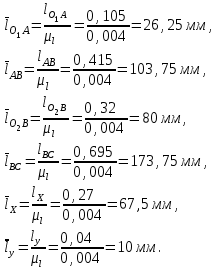 Построение диаграммы перемещений Диаграмма перемещений пятого звена является графическим изображением закона его движения. Проводим оси координат (графическая часть, лист №1). По оси абсцисс откладываем отрезок 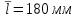 , представляющий собой в масштабе , представляющий собой в масштабе 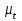 время Т(с) одного периода (время одного полного оборота выходного звена): время Т(с) одного периода (время одного полного оборота выходного звена):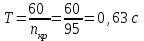 Масштабный коэффициент времени: 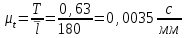 Откладываем перемещение выходного звена по оси ординат, принимаем за нулевое – крайнее нижнее положение ползуна. Масштабный коэффициент будет равен: 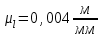 Построенная диаграмма представлена на листе №1 графической части курсового проекта. Построение диаграммы скорости Построение диаграммы скорости осуществляется методом графического дифференцирования диаграммы угла поворота (методом хорд). Н1=40мм – расстояние до полюса графического дифференцирования (Р1). Масштабный коэффициент диаграммы угловой скорости: 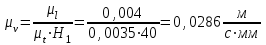 Построенная диаграмма скорости представлена на листе №1 графической части курсового проекта. Построение диаграммы ускорения Построение диаграммы ускорения осуществляется методом графического дифференцирования диаграммы угловой скорости. Н2=30мм – расстояние до полюса графического дифференцирования (Р2). Масштабный коэффициент диаграммы углового ускорения: 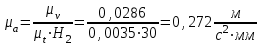 Построенная диаграмма ускорения представлена на листе №1 графической части курсового проекта. Истинные значения перемещения, скорости и ускорения приведены в таблице 4. 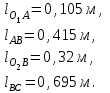 Таблица 4 - Истинные значения перемещения, скорости и ускорения
Графоаналитический метод кинематического анализа Построение плана скорости Исходные данные: Угловая скорость ведущего звена 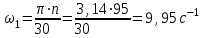 Абсолютная скорость точки А1 на конце ведущего звена 1 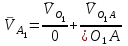 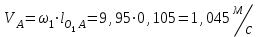 Масштабный коэффициент: 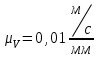 Длинна вектора скорости точки А1: 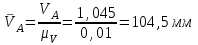 Скорость средней точки первой группы Ассура – точки В, определяем через скорости крайних точек этой группы А и О2. Скорость точки В относительно точки А: 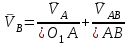 Скорость точки В относительно точки О2: 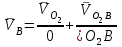 Отрезок 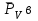 представляет собой вектор скорости точки B, решаем графически. представляет собой вектор скорости точки B, решаем графически.4. Скорость средней точки второй группы Ассура С4 определяем через скорости крайних точек этой группы В и О3. Скорость точки С4 относительно точки В: 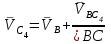 Скорость точки С4 относительно точки О3: 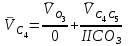 Отрезок 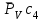 представляет собой вектор скорости точки С4, решаем графически. представляет собой вектор скорости точки С4, решаем графически.Скорости центров тяжести весомых звеньев определяем из соотношения подобия. 5. Пользуясь планом скорости, определяем истинные (абсолютные) значения скоростей точек механизма: 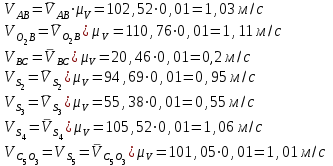 6. Определяем абсолютные величины угловых скоростей звеньев: 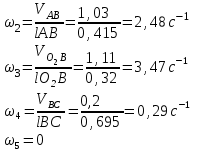 Построение плана ускорения Исходные данные: 1. Кинематическая схема механизма (1 лист) 2. Угловая скорость ведущего звена 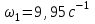 3. План скоростей для заданного положения. Абсолютное ускорение точки А на конце ведущего звена: 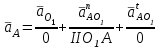 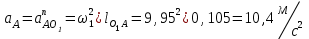 Масштабный коэффициент: 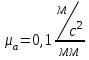 Длина вектора ускорения точки А1: 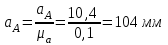 Ускорение средней точки первой группы Ассура – точки В определяем через ускорения крайних точек этой группы А и О2. Ускорение точки В относительно точки А: 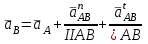 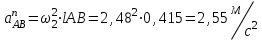 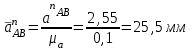 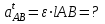 Ускорение точки В относительно точки О2: 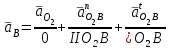 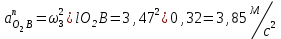 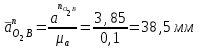 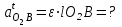 Решаем графически. Ускорение средней точки второй группы Ассура – точки С4 определяем через ускорения крайних точек этой группы В и О3, причем точка С4 принадлежит звену 4 и совпадает с точкой С5. Ускорение точки С4 относительно точки В: 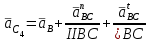 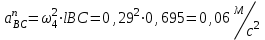 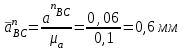 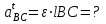 Ускорение точки С4 относительно точки О3: 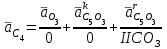 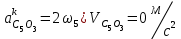 Решаем графически. Ускорения центров тяжести весомых звеньев определяем из соотношения подобия. 6. Пользуясь планом ускорений, определяем истинные (абсолютные) значения ускорений точек механизма:  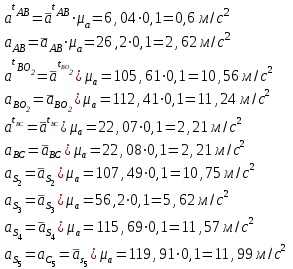 7. Определяем абсолютные величины угловых ускорений звеньев: 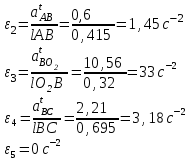 На этом кинематическое исследование кривошипно-ползунного механизма завершено. 2. Силовой анализ плоско-рычажного механизма 2.1 Определение внешних сил К звену 5 приложена сила полезного сопротивления FПС, но при заданном положении она не действует, так же к звену приложена сила линейного сопротивления FЛС (сопротивление движению или сила трения), ее направление противоположно направлению движения. Исходные данные: FЛС = 215 Н 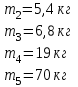 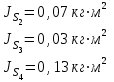 Определяем силы веса по формуле: 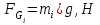 (Принимаем g=10 м/с2 – ускорение свободного падения) 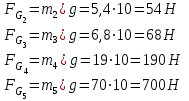 Определяем силы инерции по формуле: 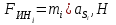 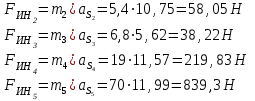 Определяем моменты пар сил инерции по формуле: 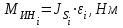 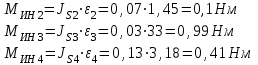 Определяем плечи переноса сил по формуле: 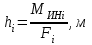 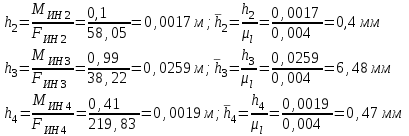 Направление внешних сил проставлено на кинематической схеме механизма (лист №1 графической части курсового проекта) 2.2 Определение внутренних сил Вторая группа Ассура Структурная группа 2 класса, 2порядка, 2 модификации. Изображаем эту группу отдельно. Действие отброшенных звеньев 3 и 0 заменяем силами реакций 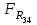 и и 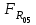 . .В точке О3 на звено 5 действует сила реакции со стороны стойки - 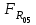 , которая перпендикулярна СО3, но неизвестна по модулю и направлению. , которая перпендикулярна СО3, но неизвестна по модулю и направлению.В точке В на звено 4 действует сила реакции со стороны звена 3 - 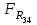 . Т. к. эта сила неизвестна по модулю и направлению, раскладываем её на нормальную и тангенсальную. Для определения тангенсальной силы . Т. к. эта сила неизвестна по модулю и направлению, раскладываем её на нормальную и тангенсальную. Для определения тангенсальной силы 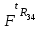 , составляем сумму моментов относительно точки С, для 4 и 5 звена. , составляем сумму моментов относительно точки С, для 4 и 5 звена.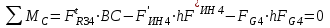 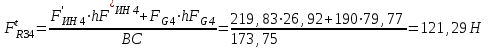 При расчете величина 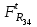 получилась со знаком (+), т. е. Направление силы выбрано верно. получилась со знаком (+), т. е. Направление силы выбрано верно.Векторное уравнение сил, действующих на звенья 4 и 5: 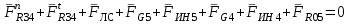 В уравнении отсутствует сила полезного сопротивления, т.к. при заданном положении она не действует. Это векторное уравнение решаем графически, т.е. строим план сил. Принимаем масштабный коэффициент: 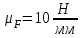 Вектора сил будут равны: 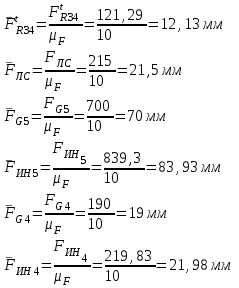 Из плана сил находим: 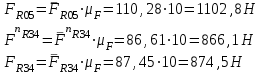 Первая группа Ассура Структурная группа 2 класса, 2порядка, 1 модификации. Изображаем эту группу отдельно. Действие отброшенных звеньев заменяем силами реакций. В точке В на звено 3 действует сила реакции со стороны звена 4 - 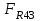 , которая равна по модулю и противоположно направлена найденной ранее силе , которая равна по модулю и противоположно направлена найденной ранее силе 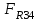 , т.е. , т.е. 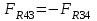 . .В точке О2 на звено 3 действует сила реакции со стороны стойки - 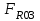 , которая известна по точке приложения и неизвестна по модулю и направлению, раскладываем её на нормальную и тангенсальную. Для определения силы , которая известна по точке приложения и неизвестна по модулю и направлению, раскладываем её на нормальную и тангенсальную. Для определения силы 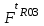 , составляем сумму моментов относительно точки В для третьего звена. , составляем сумму моментов относительно точки В для третьего звена.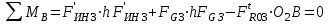 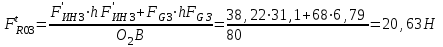 При расчете величина 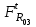 получилась со знаком (+), т. е. Направление силы выбрано верно. получилась со знаком (+), т. е. Направление силы выбрано верно.В точке А на звено 2 действует сила реакции со стороны звена 1 - 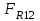 . .Линия действия этой силы неизвестна, поэтому раскладываем её на нормальную и тангенсальную. Величину 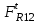 находим из уравнения моментов сил относительно точки В на звено 2. находим из уравнения моментов сил относительно точки В на звено 2.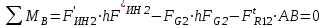 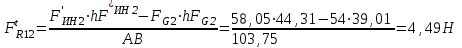 При расчете величина 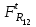 получилась со знаком (+), т. е. Направление силы выбрано верно. получилась со знаком (+), т. е. Направление силы выбрано верно.Векторное уравнение сил, действующих на звенья 2 и 3: 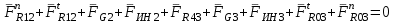 Это векторное уравнение решаем графически, т.е. строим план сил. Принимаем масштабный коэффициент: 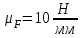 Вектора сил будут равны: 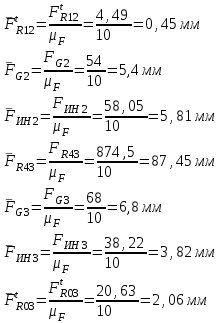 Из плана сил находим: 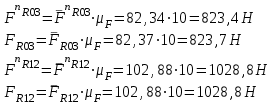 Определение уравновешивающей силы Изображаем ведущее звено и прикладываем к нему все действующие силы. Действие отброшенных звеньев заменяем силами реакций. В точке А на звено 1 действует сила реакции со стороны звена 2 - 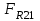 , которая равна по величине и противоположна по направлению найденной ранее силе реакции , которая равна по величине и противоположна по направлению найденной ранее силе реакции 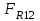 , т.е. , т.е. 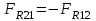 . .В точке О1 на звено 1 действует сила со стороны звена 0 - 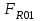 , которую необходимо определить. , которую необходимо определить.Т. к. силу тяжести первого звена не учитываем: 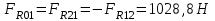 Для уравновешивания звена 1 в точках А и О1 прикладываем уравновешивающие силы - 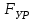 перпендикулярно звену. перпендикулярно звену.Сумма моментов относительно точки О1: 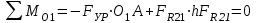 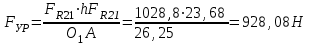 Знак 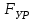 - положительный, следовательно, направление силы выбрано, верно. - положительный, следовательно, направление силы выбрано, верно.Уравновешивающий момент: 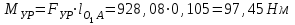 Построенный силовой анализ кривошипно-ползунного механизма изображен на листе №1 графической части курсового проекта. Определение уравновешивающей силы методом Н. Е. Жуковского. Для определения уравновешивающей силы методом Н. Е. Жуковского строим повернутый в любую сторону план скоростей. Силы, действующие на звенья механизма, переносим в соответствующие точки рычага Жуковского без изменения их направления. рычажной механизм зубчатый скольжение Плечи переноса сил на рычаге находим из свойства подобия: 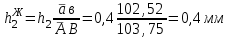 Направление плеча переноса 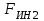 от точки S2 в сторону точки А. от точки S2 в сторону точки А.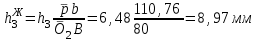 Направление плеча переноса 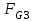 от точки S3 в сторону точки В. от точки S3 в сторону точки В.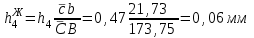 Направление плеча переноса 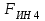 от точки S4 в сторону точки С. от точки S4 в сторону точки С.Уравнение моментов сил, действующих на рычаг относительно полюса: 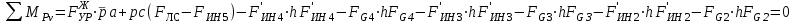 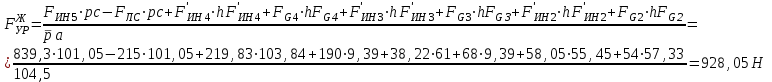 Уравновешивающий момент: 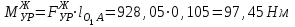 Определение погрешности. Сравниваем полученные значения уравновешивающего момента, используя формулу: 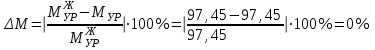 Допустимые значения погрешности менее 3% следовательно, расчеты произведены верно. На этом силовой анализ кривошипно-ползунного механизма закончен. 3. Синтез зубчатого механизма 3.1 Геометрический синтез зубчатого зацепления Задачей геометрического синтеза зубчатого зацепления является определение его геометрических размеров и качественных характеристик (коэффициентов перекрытия, относительного скольжения и удельного давления), зависящих от геометрии зацепления. 3.2 Определение размеров внешнего зубчатого зацепления Исходные данные: Z4 = 12 – число зубьев шестерни, Z5 = 30 – число зубьев колеса, m2 = 10 – модуль зацепления. Шаг зацепления по делительной окружности 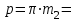 3,14159 · 10 = 31,41593 мм 3,14159 · 10 = 31,41593 ммРадиусы делительных окружностей 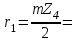 10 · 12 / 2 = 60 мм 10 · 12 / 2 = 60 мм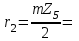 10 · 30 / 2 = 150 мм 10 · 30 / 2 = 150 ммРадиусы основных окружностей 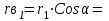 60 · Соs20o = 60 · 0,939693 = 56,38156 мм 60 · Соs20o = 60 · 0,939693 = 56,38156 мм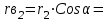 150 · Соs20o = 150 · 0,939693 = 140,95391 мм 150 · Соs20o = 150 · 0,939693 = 140,95391 ммКоэффициенты смещения Х1 – принимаем равным 0,73 т.к. Z4 =12 Х2 – принимаем равным 0,488 т.к. Z5 =30 Коэффициенты смещения выбраны с помощью таблиц Кудрявцева. 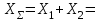 0,73 + 0,488 = 1,218 0,73 + 0,488 = 1,218Толщина зуба по делительной окружности 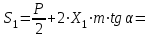 31,41593 / 2 + 2 · 0,73 · 10 · 0,36397 = 21,02192 мм 31,41593 / 2 + 2 · 0,73 · 10 · 0,36397 = 21,02192 мм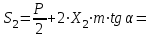 31,41593 / 2 + 2 · 0,488 · 10 · 0,36397 = 19,26031 мм 31,41593 / 2 + 2 · 0,488 · 10 · 0,36397 = 19,26031 ммУгол зацепления Для определения угла зацепления вычисляем: 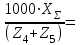 1000 · 1,218 / (12 + 30 ) = 29 1000 · 1,218 / (12 + 30 ) = 29С помощью номограммы Кудрявцева принимаем 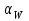 =26о29'=26,48о =26о29'=26,48оМежосевое расстояние 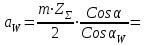 (10·42/2) · Соs20o / Cos26,48o=210·0,939693 / 0,89509 = 220,46446 мм (10·42/2) · Соs20o / Cos26,48o=210·0,939693 / 0,89509 = 220,46446 ммКоэффициент воспринимаемого смещения 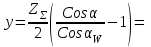 ( 42 / 2 ) · ( 0,939693 / 0,89509 – 1 ) = 21 · 0,04983 = 1,04645 ( 42 / 2 ) · ( 0,939693 / 0,89509 – 1 ) = 21 · 0,04983 = 1,04645Коэффициент уравнительного смещения 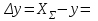 1,218 – 1,04645 = 0,17155 1,218 – 1,04645 = 0,17155Радиусы окружностей впадин 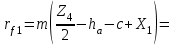 10 · ( 12 / 2 – 1 – 0,25 + 0,73 ) = 54,8 мм 10 · ( 12 / 2 – 1 – 0,25 + 0,73 ) = 54,8 мм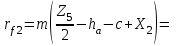 10 · (30 / 2 – 1 – 0,25 + 0,488 ) = 142,38 мм 10 · (30 / 2 – 1 – 0,25 + 0,488 ) = 142,38 ммРадиусы окружностей головок 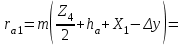 10 · ( 12 / 2 + 1 + 0,73 – 0,17155 ) =75,5845мм 10 · ( 12 / 2 + 1 + 0,73 – 0,17155 ) =75,5845мм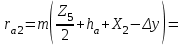 10 · (30 / 2 + 1 + 0,488 – 0,17155 ) =163,1645мм 10 · (30 / 2 + 1 + 0,488 – 0,17155 ) =163,1645ммРадиусы начальных окружностей 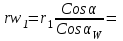 56 · 0,939693 / 0,89509 = 62,98984мм 56 · 0,939693 / 0,89509 = 62,98984мм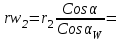 150 · 0,939693 / 0,89509 = 157,47461мм 150 · 0,939693 / 0,89509 = 157,47461ммГлубина захода зубьев 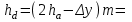 ( 2 · 1 – 0,17155 ) · 10 = 18,2845 мм ( 2 · 1 – 0,17155 ) · 10 = 18,2845 ммВысота зуба 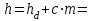 18,2845 + 0,25 · 10 = 20,7845 мм 18,2845 + 0,25 · 10 = 20,7845 ммПроверка: 1. 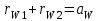 62,98984 + 157,47461 = 220,46445 условие выполнено 2. 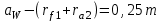 220,46446 – ( 54,8 + 163,1645 ) = 0,25 · 10 220,46446 – 217,9645 = 2,5 условие выполнено 3. 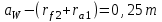 220,46446 – ( 134,176 + 75,5845 ) = 0,25 · 10 220,46446 – 217,9645 = 2,5 условие выполнено 4. 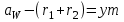 220,46446 – ( 60 + 150 ) = 1,04645 · 10 220,46446 – 210 = 10,4645 условие выполнено Список использованных источников Артоболевский И.И. Теория механизмов и машин. – М.: «Наука», 1975г. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. – Киев: «Высшая школа», 1970г. Фролов К.В. Теория механизмов и машин. – М.: «Высшая школа», 1987г. Попов С.А. Курсовое проектирование по теории механизмов и машин. – М.: «Высшая школа», 1986г. 5. Методические указания по теме Курсовое проектирование по теории механизмов и машин. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||