|
Курсовой проект 106 страниц, 42 рисунка, 2 таблицы, 18 фомул, 15 матриц, 4 приложения
Эллипсоид в графической базе данных задается следующими параметрами:
r – радиус эллипсоида;
h – половина высоты эллипсоида;
n – количество разбиений на вертикальной полуокружности,
m – количество разбиений на горизонтальной полуокружности.
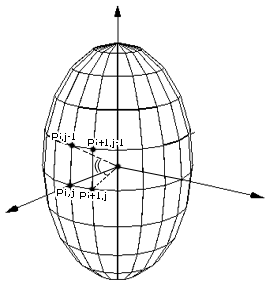
Рассмотрим построение геометрической модели эллипсоида с помощью меридиан и параллелей, центр локальной системы координат свяжем с геометрическим центром эллипсоида, оси которой направлены произвольно. Построение геометрической модели представлено на рисунке 4.6.
z
y
x
0
β
α
Рисунок 4.6 – Модель эллипсоида
Построение эллипсоида начинаем с построения точки с координатами Р00(0, 0, r). Затем строится нулевой меридиан (кривая разбивается на n точек) по формуле:
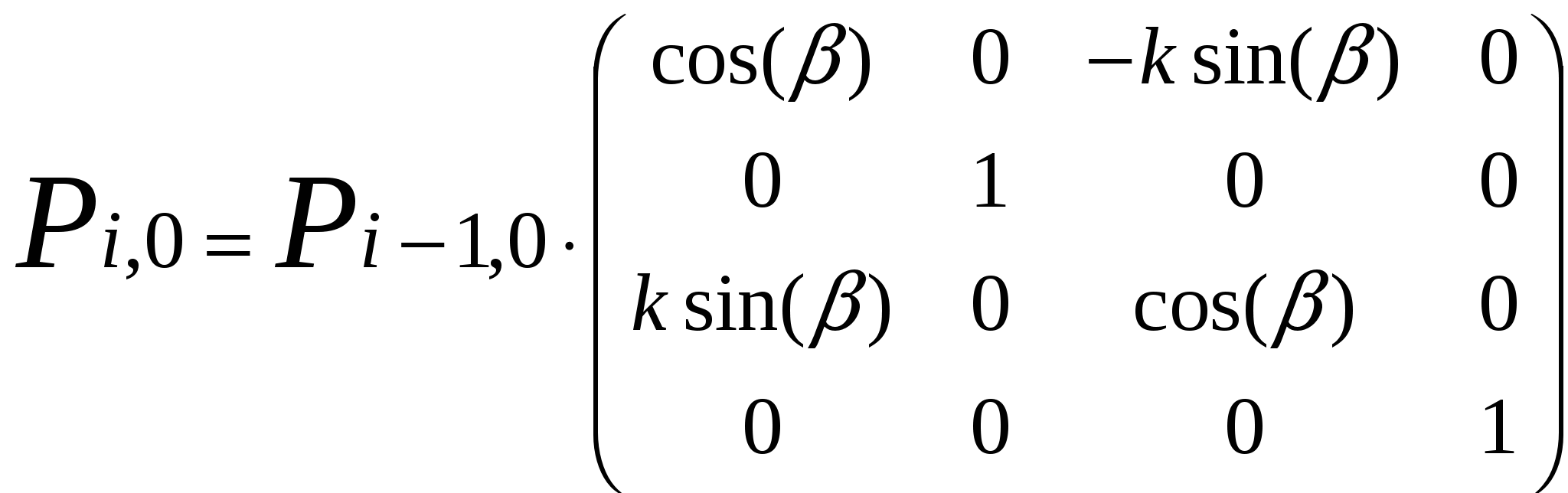
(4.9)
,
где 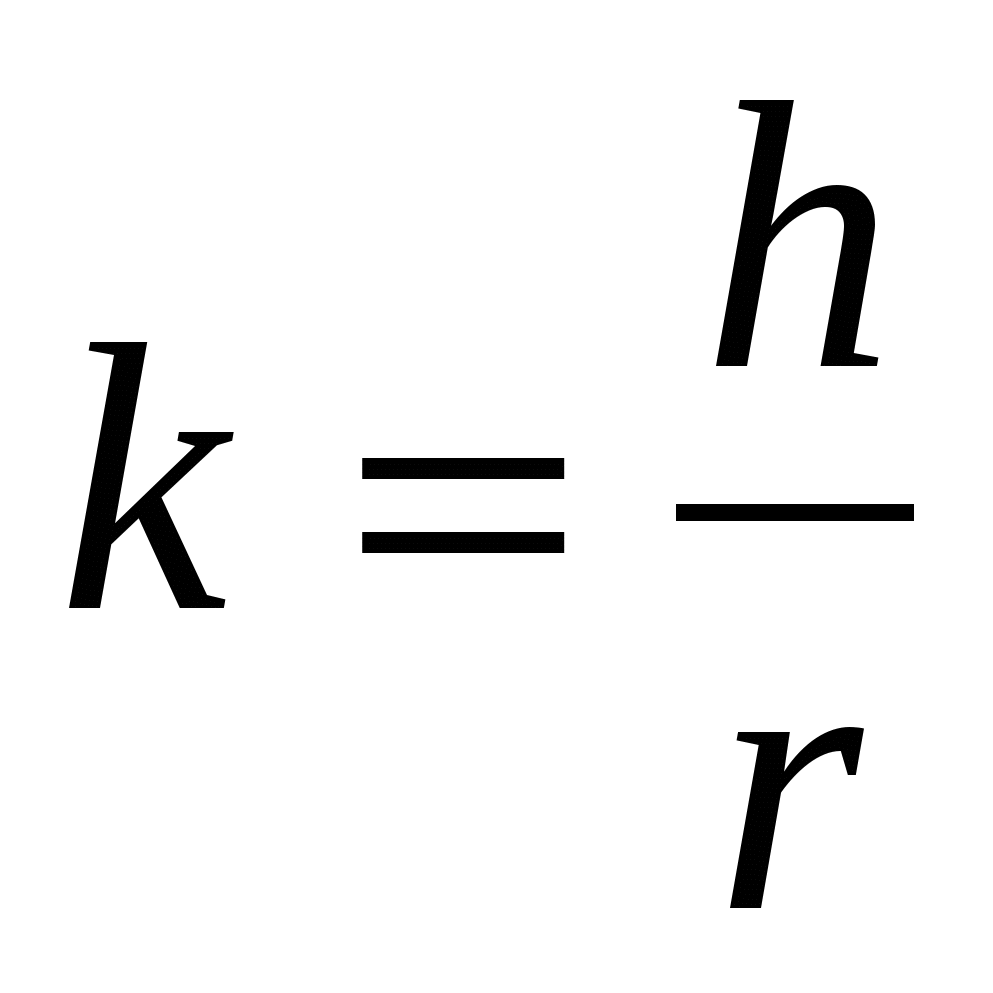 - коэффициент растяжения; - коэффициент растяжения;
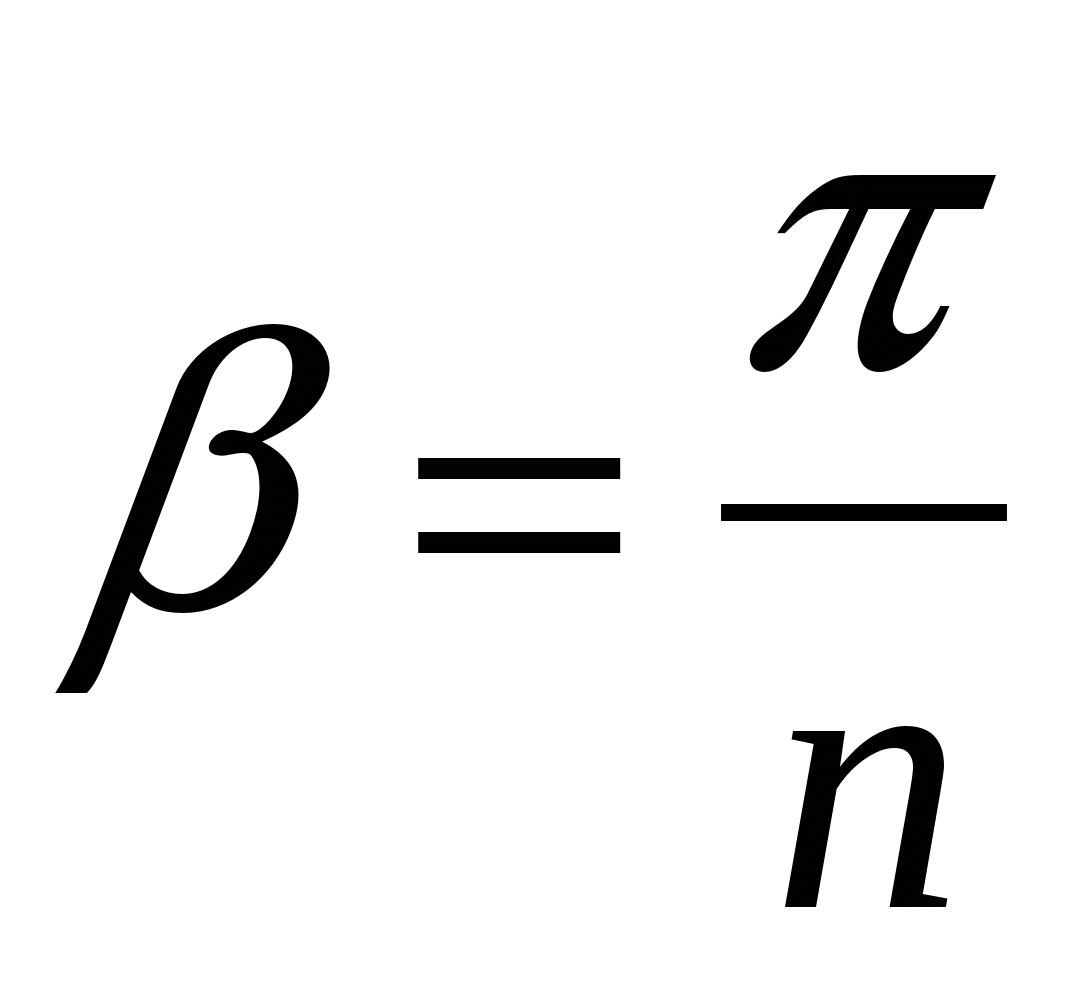 - угол поворота. - угол поворота.
Построенная ломаная, точки P0,0…Pn,0 - нулевой меридиан.
Построение параллелей производится путем вращения нулевого меридиана вокруг оси Z на угол α = 2π/m.
Следовательно, в графической базе данных модель эллипсоида можно задать с помощью формулы (4.10):
Эллипсоид(r,h,n,m) (4.10)
где r – радиус эллипсоида, h – высота половыны эллипсоида, n - количество меридиан, m - количество параллелей.
4.7 Геометрическая модель косоугольного конуса
Косоугольный конус задаётся четырьмя параметрами: высота, радиус основания, смещение вершины конуса относительно центра основания вдоль оси OX, количество разбиений основания. Обозначим эти параметры соответственно буквами h, r, s и n.
Пусть центр основания совпадает с началом локальной системы координат, а часть конуса без основания находится со стороны положительного направления оси OZ. Первая точка основания имеет координаты A1=(0, r, 0). Тогда координаты остальных точек снования будем находить по следующей формуле:
Ai+1= Ai*ПоворотOZ(360/n), (4.11)
а координаты вершины конуса будут равны (s, 0, h).
Вид геометрической модели косоугольного конуса приведен на рисунке 4.6.
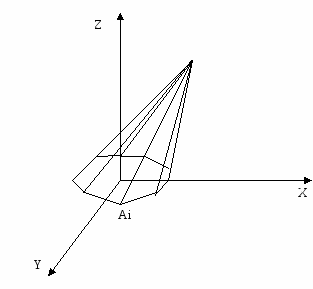
Рисунок 4.6 – Вид геометрической модели косоугольного конуса
4.8 Геометрическая модель пирамиды с пятиугольным основанием
Пирамида с пятиугольным основанием задаётся двумя параметрами: высота и радиус окружности, в которую вписано основание. Обозначим эти параметры соответственно буквами h и r.
Пусть центр основания совпадает с началом локальной системы координат, а часть пирамиды без основания находится со стороны положительного направления оси OZ. Первая точка основания имеет координаты A1=(0, r, 0). Тогда координаты остальных точек снования будем находить по следующей формуле:
Ai+1= Ai*ПоворотOZ(360/5), (4.12)
а координаты вершины конуса будут равны (0, 0, h).
Вид геометрической модели пирамиды с пятиугольным основанием приведен на рисунке 4.7.
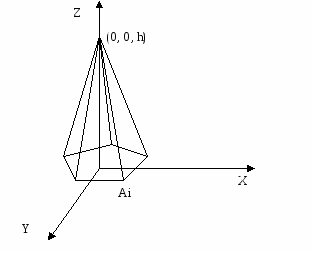
Рисунок 4.7 – Вид геометрической модели пирамиды с пятиугольным основанием
4.9 Геометрическая модель усечённой пирамиды с трёугольным основанием
Данный объект задаётся тремя параметрами: высота, радиус окружности, в которую вписано нижнее основание и радиус окружности, в которую вписано верхнее основание. Обозначим эти параметры соответственно буквами h, r1 и r2.
Пусть центр нижнего основания совпадает с началом локальной системы координат, а часть пирамиды без этого основания находится со стороны положительного направления оси OZ. Первая точка нижнего основания имеет координаты A11=(0, r1, 0), а первая точка верхнего основания A21=(0, r2, h). Тогда координаты остальных точек нижнего снования будем находить по следующей формуле:
A1i+1= A1i*ПоворотOZ(360/3), (4.13)
а координаты точек верхнего основания – по формуле:
A2i+1= A2i*ПоворотOZ(360/3). (4.14)
Вид геометрической модели усеченной пирамиды с треугольным основанием приведен на рисунке 4.8.
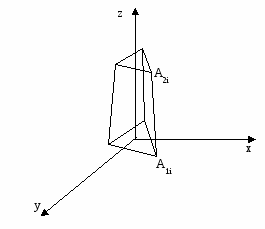
Рисунок 4.8 – Геометрическая модель усечённой пирамиды с трёугольным основанием
4.10 Моделирование икосаэдра
Для построения икосаэдра (рис. 4.9) используется цилиндр радиуса R , ось Z которого совпадает с осью цилиндра, а основание находится друг от друга на расстоянии ± h/2.
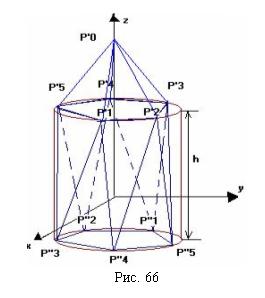
Рисунок 4.9 Построение икосаэдра
Каждое из окружностей оснований разбивается на 5 равных сегментов, и точки окружности последовательно соединяются между собой. Вращаясь против часовой стрелки на угол φ = 2*π /5, выбираются точки на первой и на второй окружности соответственно.
На высоте: 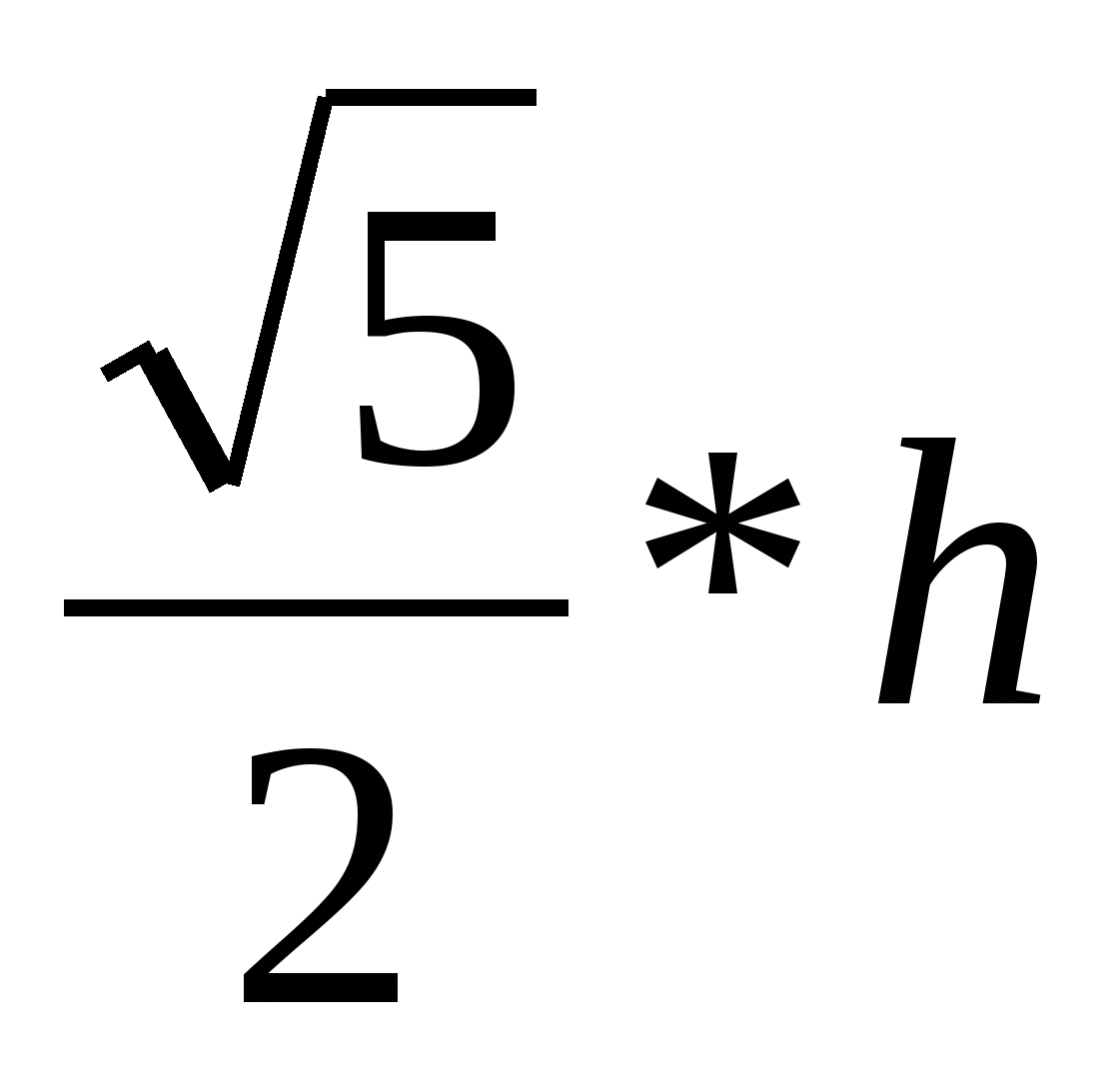 выбираются вершины P'0 и P''0 и соединяются с вершинами в основании (верхнего и нижнего соответственно). выбираются вершины P'0 и P''0 и соединяются с вершинами в основании (верхнего и нижнего соответственно).
Остальные вершины получаются с помощью матрицы поворота:
P’i= P’i-1*Поворот(2*π/5) (4.1)
P"i= P”i-1*Поворот(2* π /5) (4.2)
Модель построенного икосаэдра изображена на рисунке 4.10.
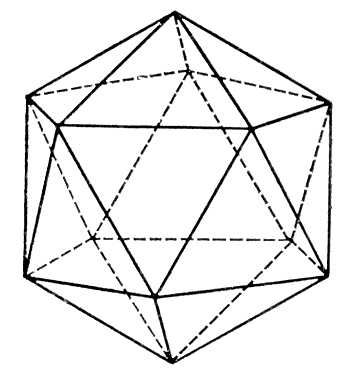
Рисунок 4.10 – Модель икосаэдра
4.11 Геометрическая модель додекаэдра
Построение додекаэдра осуществляется при помощи икосаэдра.
Ниже приведены краткие шаги данной операции.
Построение икосаэдра;
Определение геометрических центров каждой из граней;
Соединение геометрических центров.
Для построения икосаэдра используется цилиндр единичного радиуса R, ось которого совпадает с осью OZ, и основание находится соответственно на высоте 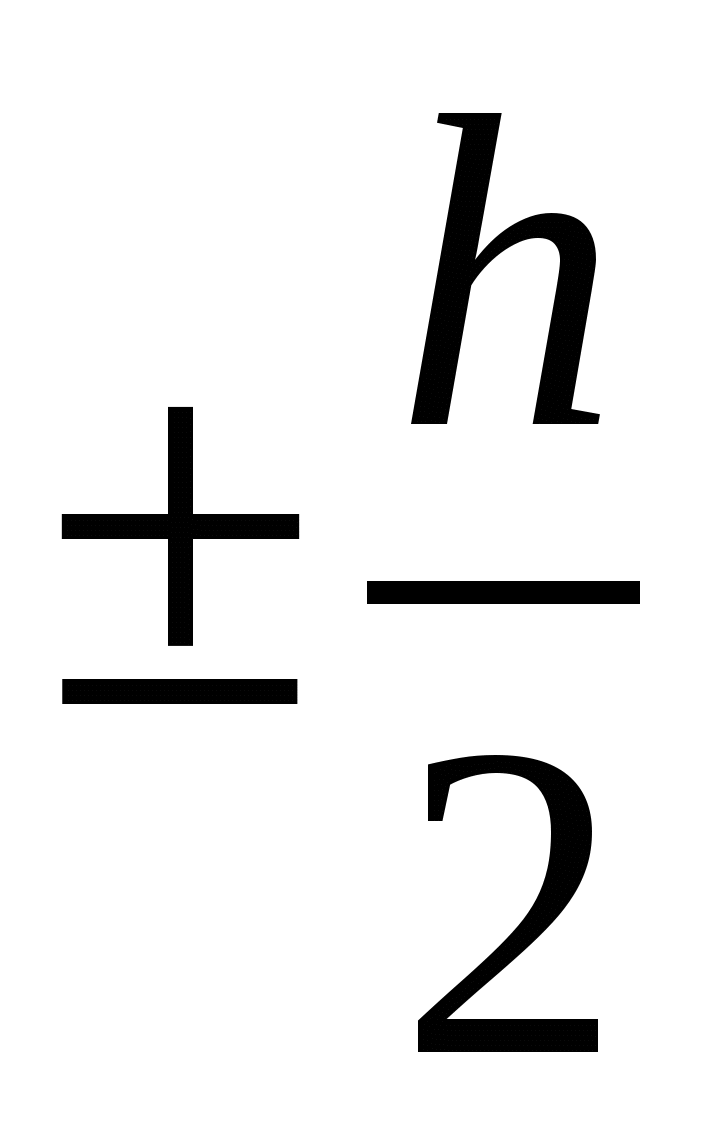 . Каждая из окружностей разбивается на 5 равных сегментов, и точки на окружности последовательно соединяются между собой. . Каждая из окружностей разбивается на 5 равных сегментов, и точки на окружности последовательно соединяются между собой.
Двигаясь против часовой стрелки с шагом α=2π/n, выбираются точки то на одной, то на другой окружности. Далее происходит попарно соединение точек. На высоте 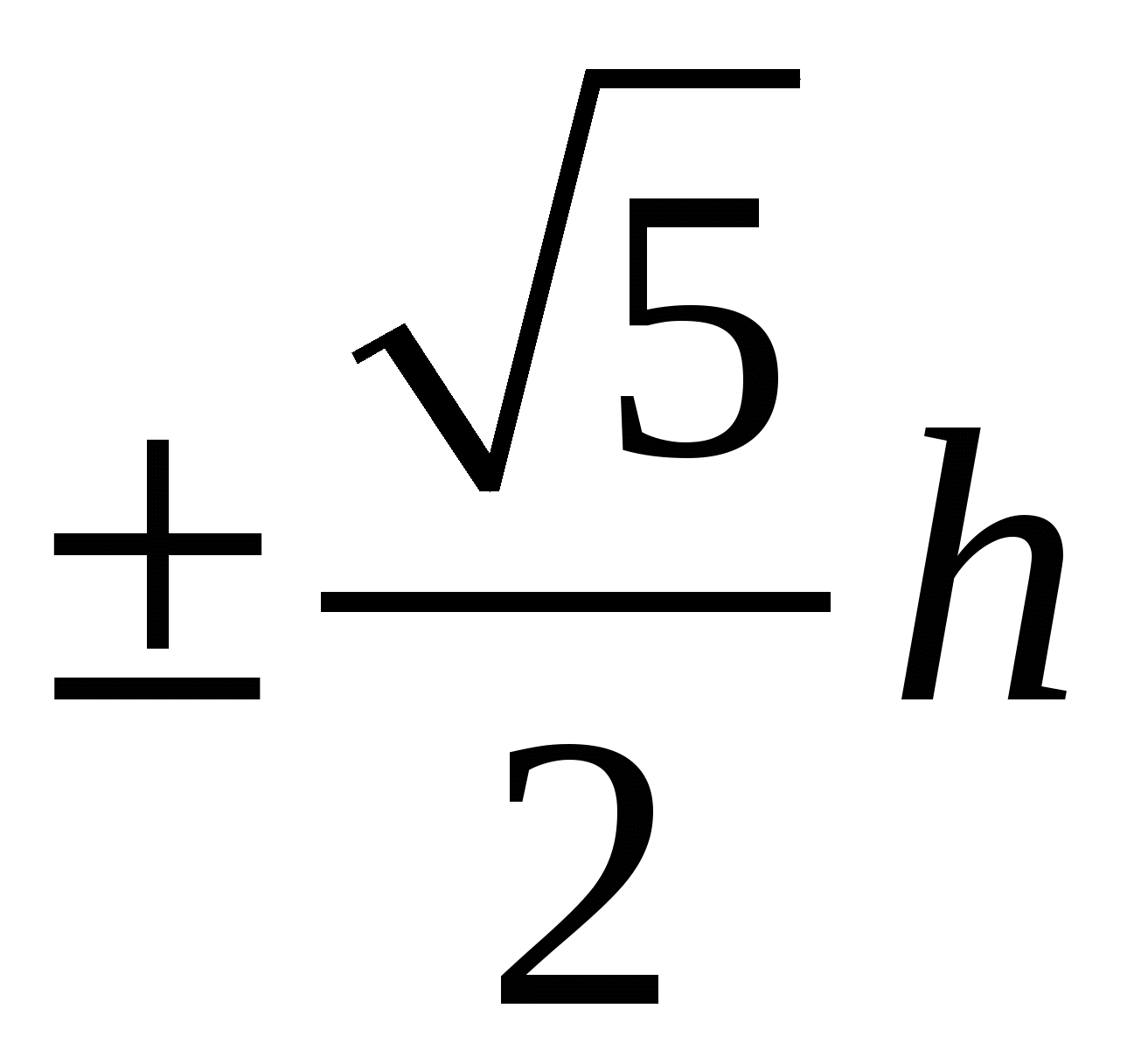 берется окончательная вершина. берется окончательная вершина.
В графической базе данных додекаэдр можно представить в виде:
Додекаэдр(W), (4.15)
где w – длина стороны.
На рисунке 4.11 изображена геометрическая модель додекаэдра.
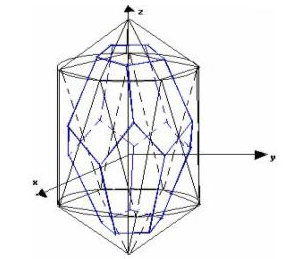
Рисунок 4.11 – Геометрическая модель додекаэдра
5 ПОШАГОВОЕ ПОСТРОЕНИЕ МОДЕЛИ СЛОЖНОГО ОБЪЕКТА
5.1 Декомпозиция сложного объекта
Моделью сложного трехмерного объекта, согласно заданию, является модель робота-краба, которая состоит из таких базовых примитивов как: эллипсоид, икосаэдр, призма с треугольным основанием, сфера, косоугольный цилиндр, усеченная пирамида с треугольным основанием, полусфера, косоугольная призма с треугольным основанием.
Модель робота-краба состоит из лап (призма с треугольным основанием, икосаэдр, усеченная пирамида с треугольным основанием), лап (косоугольный цилиндр) с клещнями (косоугольная призма с теугольным основанием), глаз (сфера), тело (полусфера, элипсоид).
5.2 Параметрические модели примитивов
Лапа состоит из следующих примитивов:
- призма с треугольным основанием Prizm3(r1, h1);
- икосаэдр Iko(r2);
- усеченная пирамида с треугольным основанием Piramid3(r3, r4, h2,).
Лапа с клещами состоит из следующих примитивов:
- косоугольный цилиндр Cyl(r5, h3, n1,m1)*M(сдвига);
- косоугольная призма с теугольным основанием KosPr(r6, h4)* *M(сдвига).
Глаз состоит из следующих примитивов:
- сфера Sphere (r7, n2, m2).
Тело состоит из следующих примитивов:
- полусфера Halfsphere(r8, n3, m3)*M(отсечения);
- элипсоид Elips(r9, n4, m4)*M(сжатия),
где r(i) – радиус, h(i) – высота, n(i), m(i) - число разбиения, М – матрица.
n1=n2=n3=n
m1=m2=m3=m
Запишем значения параметром фигур через r7:
h1=20*r7;
h2=r7;
h3=18*r7
h4=4*r7
r1=1.5*r7;
r2=r7;
r3=r7;
r4=2*r7;
r5=1.5*r7;
r6=1.5*r7;
r8=9*r7
r9=12*r7;
5.3 Пошаговое построение сложного объекта
Строим тело:
- Стоим элипосид:
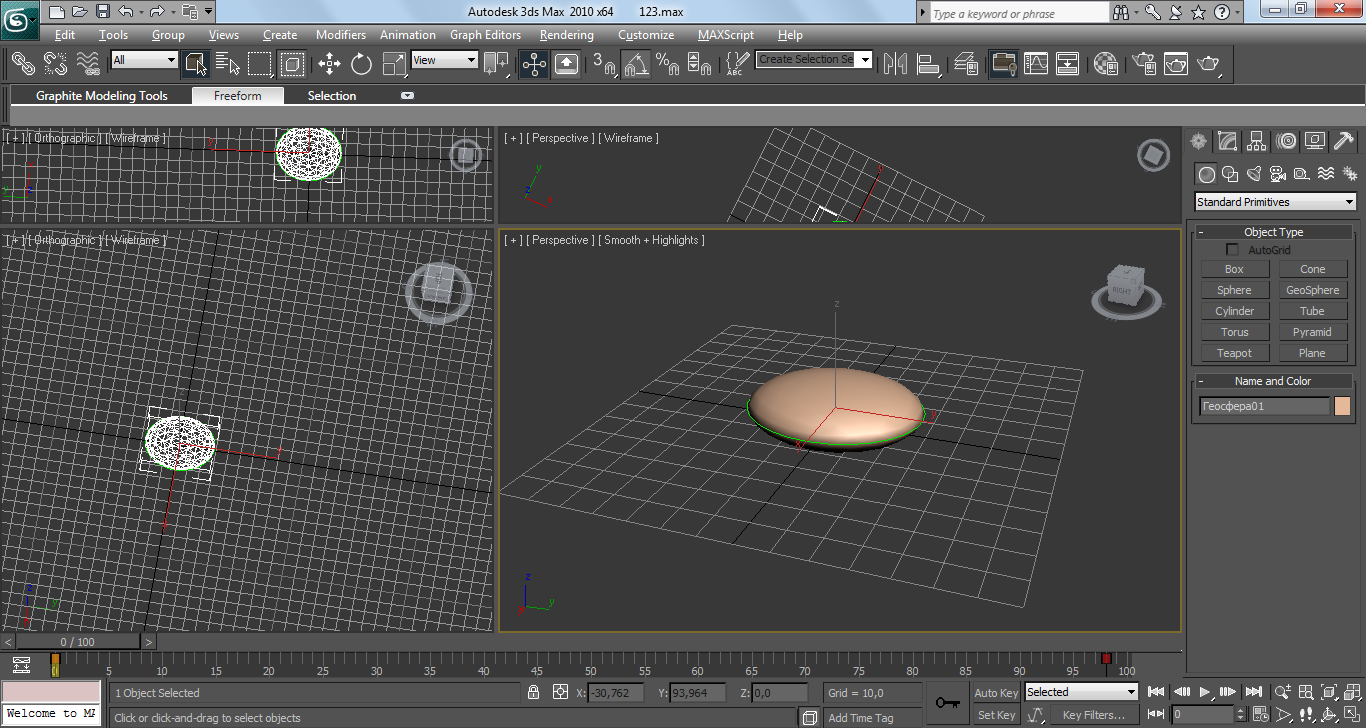
Строим сферу радиусом 12*r7, умножаем на матрицу сжатия М(0.8, 1, 0.25), получаем элипсоид (рисунок 5.1).
Z
Y
X
Рисунок 5.1 – Эллипсоид
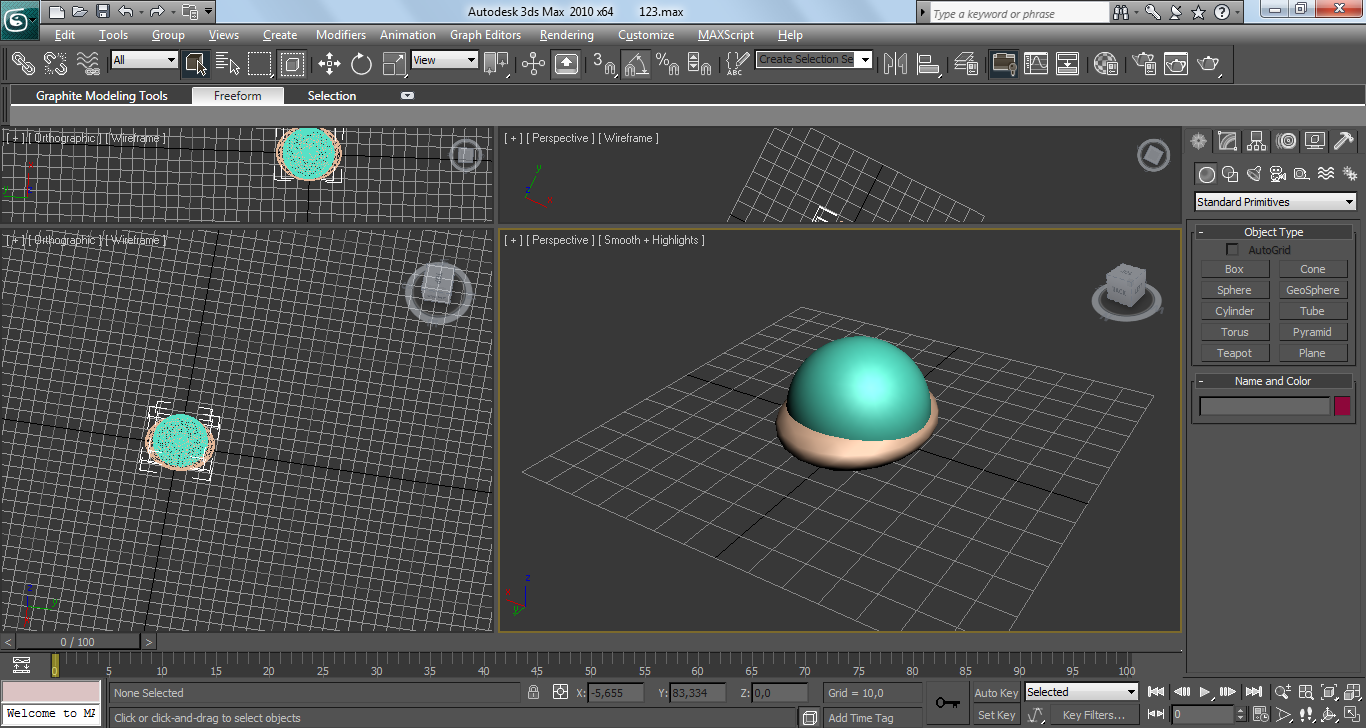
Строим полусферу:
- cтроим сферу радиусом 9*r7. Отсекаем пол сферу по оси –OZ.
Полученная фигура будет телом (рисунок 5.2).
Z
-X
Y
Рисунок 5.2- Тело
Строим глаза:
1 глаз:
- cтроим сферу радиусом r7. Переносим на (4*r7, 3*r7, 8*r7);
2 глаз:
- строим сферу радиусом r7. Переносим на (-4*r7, 3*r7, 8*r7).
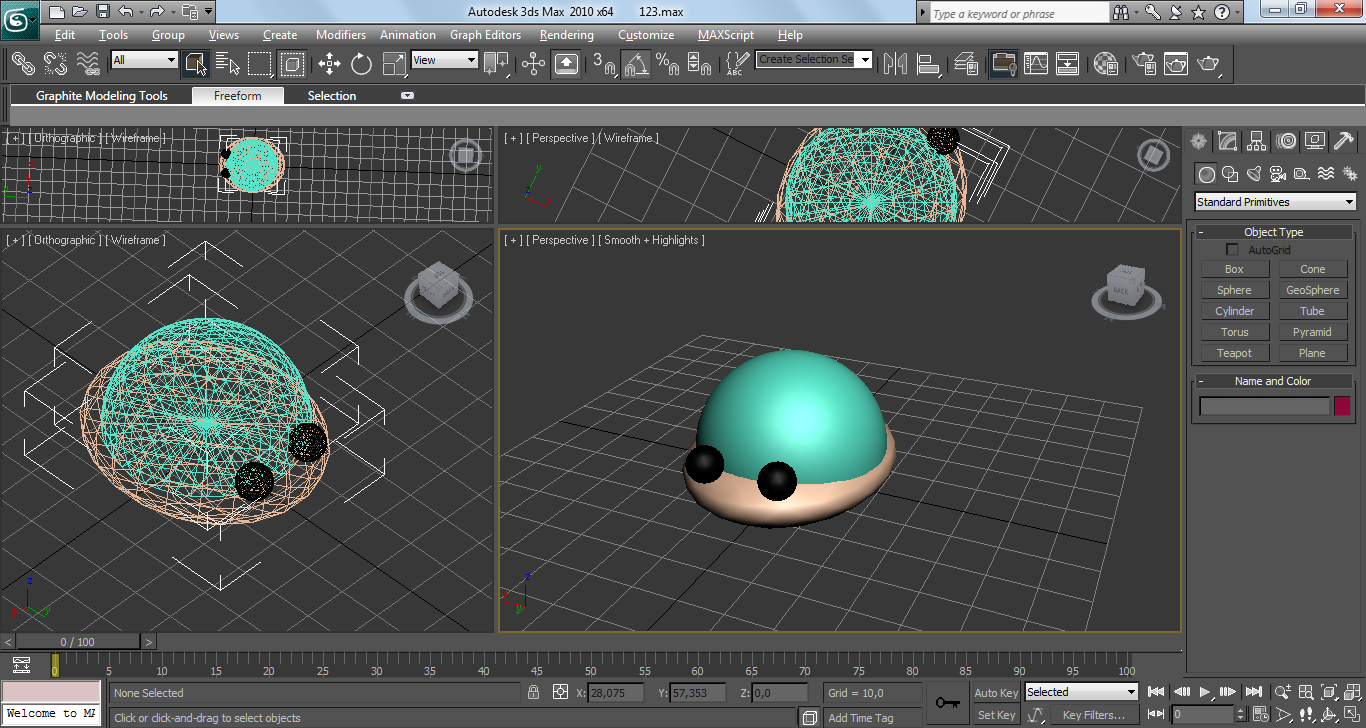
Полученная фигура будет телом с глазами (рисунок 5.3)
Z
-X
Y
Рисунок 5.2- Тело с глазами
Строим лапы:
- строим призму с треугольным основанием:
- строим цилиндр с числом разбиения равным 3, радиуса 1.5*r7 и высотой 20*r7;
- строим икосаэдр
строим икосаэдр радиусом r7 и перемещаем на (0, 0, 20*r7);
- строим усеченную призму с треугольным основанием:
строим цилиндр с числом разбиения равным 3, радиусами r7, 2*r7 и высотой r7, поворачиваем вокруг оси OY на -90 градусов, перемещаем на (0, 0, 3*h-2/5h).
1 лапа:
- поворачиваем построенные фигуры на 90 градусов вокруг оси OX и 45 градусов вокруг оси OZ;
2 лапа:
- поворачиваем построенные фигуры на 90 градусов вокруг оси OX и -45 градусов вокруг оси OZ;
3 лапа:
- поворачиваем построенные фигуры на -90 градусов вокруг оси OX и 45 градусов вокруг оси OZ;
4 лапа:
- поворачиваем построенные фигуры на -90 градусов вокруг оси OX и -45 градусов вокруг оси OZ;
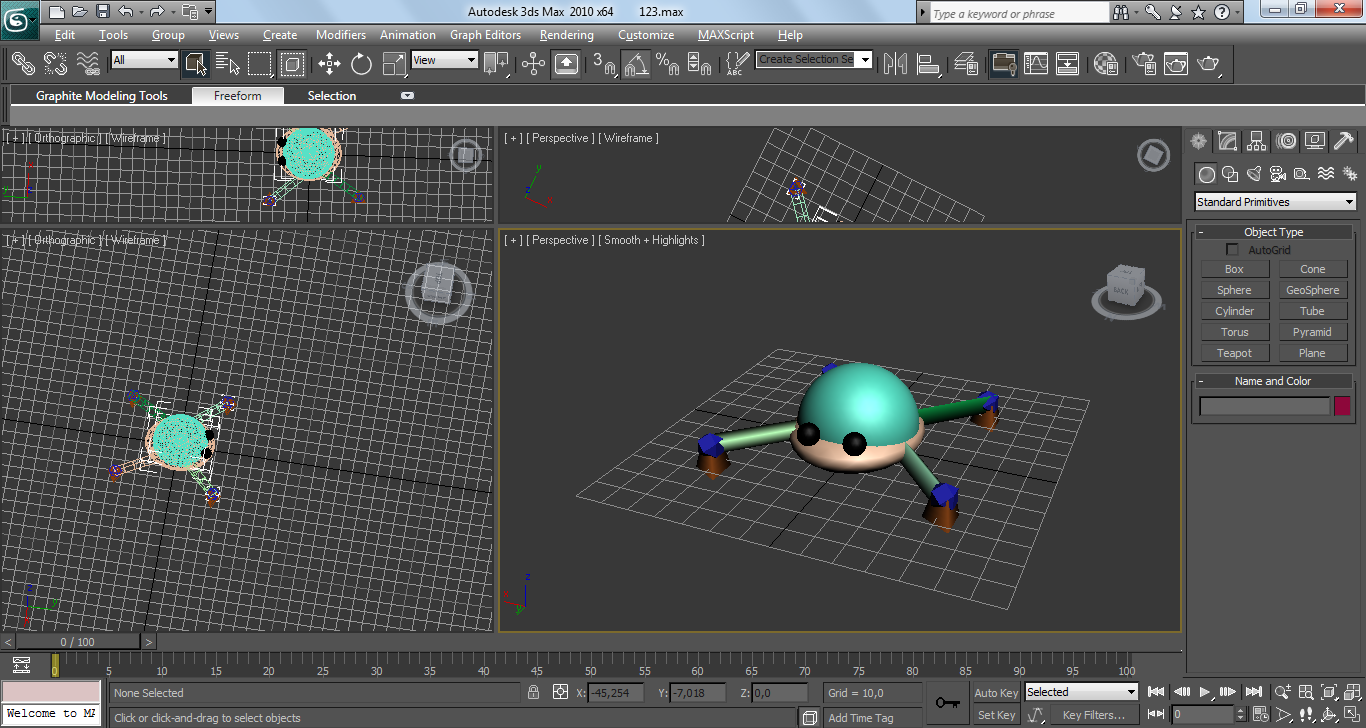
Полученная фигура будет содержать лапы (рисунок 5.3)
Z
-X
Y
Рисунок 5.3 - Фигура с лапами
Строим лапы с клещнями:
- строим косоугольный цилиндр:
- строим цилиндр радиусом 1.5*r7, высотой 20*r7, сдвигаем по оси OY на 0.1*r7
- строим косоугольную призму с треугольным основанием:
- строим цилиндр с числом разбиения равным 3, радиусом 1.5*r7, высотой 18*r7, сдвигаем по оси OX на 0.1*r7, перемещаем на 4*r7;
- Поворачиваем полученные фигуры на 90 градусов вокруг оси OX.
1 лапа с клещней:
- поворачиваем полученные фигуры на 30 градусов вокруг оси OY;
2 лапа с клещней:
- поворачиваем полученные фигуры на -30 градусов вокруг оси OY.
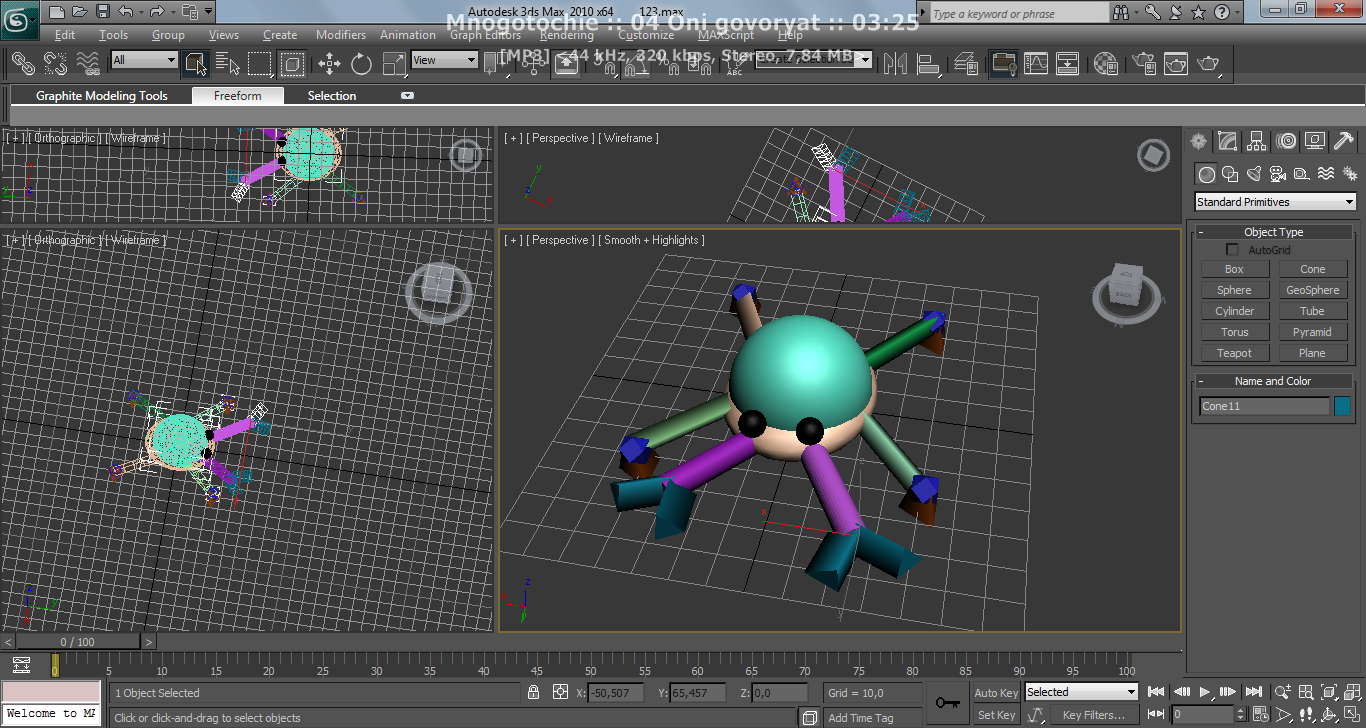
Получили робота-краба (рисунок 5.4)

Z
-X
Y
Рисунок 5.4 - Робот-краб
6 ОПИСАНИЕ ПРОГРАММНОЙ РЕАЛИЗАЦИИ
6.1 Структуры данных для хранения параметрических объектов
В данном курсовом проекте описаны классы, упрощающие работу с 3D-примитивами, информационной частью данных классов являются структуры данных, хранящие параметры объектов. Иерархия данных классов описывается диаграммой на рисунке 6.1.
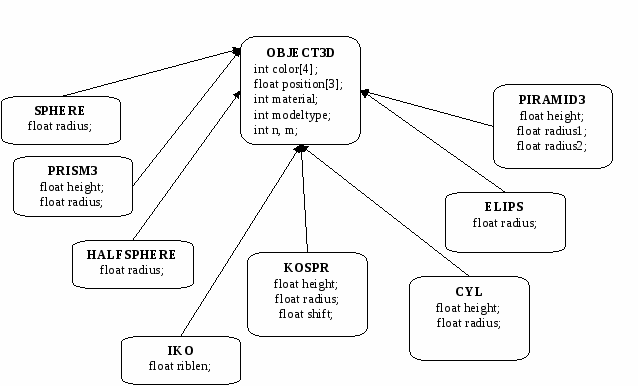
Рисунок 6.1 – Иерархия классов, содержащих параметры объектов сцены
6.2 Структуры данных для камеры
В реализуемом программном продукте структура данных для камеры описывается на языке C++ следующим образом:
struct
{
float posx, posy, posz;
float dirx, diry, dirz;
}settings, где
posx, posy, и posz –соответственно координаты наблюдателя, а dirx, diry, dirz – соответственно координаты направляющего вектора.
6.3 Структуры данных для источников света
В реализуемом программном продукте структура данных для источников света описывается на языке C++ следующим образом:
struct
{
float pos[4];
float dir[3];
float color[4];
int lightmodeltype;
bool shining;
} settings, где
pos – массив координат источника света, dir – массив координат напрвляющего вектора, color – массив, содержащий цвет излучаемого света в формате RGBA, lightmodeltype – тип источника света (точечный, удалённый, цилиндрический), shining – признак включенности источника света.
Выше приведена структура данных заключена в класс, написанный для облегчения работы с источниками света, имеющий следующий протокол
class LIGHT
{
struct{
float pos[4];
float dir[3];
float color[4];
int lightmodeltype;
GLboolean shining;
} settings;
int index;
public:
void Draw();
GLenum GetIndex();
bool Shining();
LIGHT& TurnOn();
LIGHT& TurnOff();
LIGHT(int gllight):index(gllight);
LIGHT(){glDisable(index);}
void SetLightModelType(int lmt);
void Dispose(float PosX, float PosY, float PosZ, float PosT);
LIGHT& Direct(float DirX, float DirY, float DirZ);
LIGHT& SetColor(float r, float g, float b);
void GetPosition(float *x, float *y, float *z);
void GetDirection(float *x, float *y, float *z);
void GetColor(float *r, float *g, float *b);
};
6.4 Описание внутреннего формата графической БД
Графическая база данных реализуемого программного продукта организована в виде набора структур данных, содержащих параметры графических примитивов, камеры и источников. К операциям, осуществимым над графической базой данных, относятся добавление, удаление и поиск графических примитивов, а также изменение их параметров.
6.5 Описание формата файла хранения сцены
Файл, содержащий параметры сцены имеет формат, показанный на таблице 6.1.
Таблица 6.1 – Описание формата файла хранения сцены
Название блока
|
Размер блока в байтах
|
Параметры графических примитивов
|
508
|
Параметры источников света
|
236
|
Параметры камеры
|
85
|
Матрица модельно-видовых преобразований
|
64
|
Параметры интерфейса программы
|
18
|
Размер файла хранения сцены составляет 911 байт.
6.6 Описание программных моделей
Для удобства построения системы трехмерного графического моделирования программа была разбита на следующие модули:
- KP.cpp – главный программный модель;
- globals.h – файл, содержащий описание глобальных переменных, доступных из всех программных модулей;
- glsetup.h – файл, содержащий подпрограммы, служащие для установки матриц проекций и областей просмотров;
- primitives.h – файл, содержащий описание протоколов и реализации классов, упрощающих работу с графическими примитивами;
- light.h – файл, содержащий описание протоколов и реализации классов, упрощающих работу с источниками света;
- camera.h – файл, содержащий описание протокола и реализацию классоа, упрощающего работу с камерой;
- drawscene.h - файл, содержищий подпрограммы отрисовки сцены;
- mainwnd.h - файл, содержищий описание функций для работы с главным окном программы;
- panel.h – файл, содержищий описание функций для работы с панелью управления в главном окне программы;
- panel_aff_aj.h, panel_camera.h, panel_light.h, panel_primitives.h, panel_scene.h – модули, касающиеся построения интерфейса программы, содержащие реализацию подпрограмм, описывающих поведение диалоговых панелей, позволяющих пользователю изменять параметры камеры, графических примитивов, источников света и сцены, а также осуществлять аффинные преобразования.
Взаимосвязь программных модулей показана на рисунке 6.2.
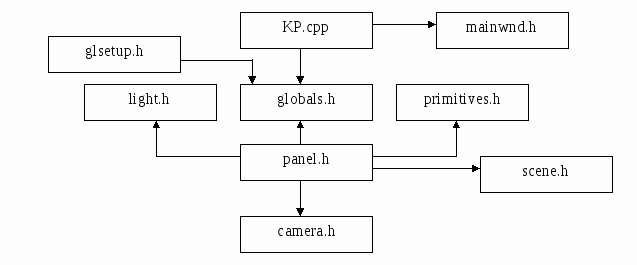
Рисунок 6.2 - Взаимосвязь программных модулей
6.7 Описание основных процедур и функций
Программный продукт, реализуемый в данном курсовом проекте, разбит на функции следующих категорий:
1) функции настройки графического вывода:
- void glSetViewport(int vp). Устанавливает область вывода. vp – параметр, задающий область вывода, которую необходимо установить;
- void SetOrtho(). Устанавливает ортографическую проекцию;
- void SetIso(). Устанавливает изометрическую проекцию.
2) Функции отрисовки графических примитивов и визуализации источников света:
- void SPHERE::Draw(). Функция отрисовки сферы;
- void HALFSPHERE::Draw(). Функция отрисовки полусферы;
- void CUBE::Draw(). Функция отрисовки куба;
- void PRISM5::Draw(). Функция отрисовки пятигранной пизмы;
- void PRISM3::Draw(). Функция отрисовки трёхгранной призмы;
- void PIRAMID::Draw(). Функция отрисовки пирамиды с пятиугольным основанием;
- void PIRAMID3::Draw(). Функция отрисовки усечённой пирамиды с трёхугольным основанием;
- void CONE::Draw(). Функция отрисовки косоугольного конуса;
- void LIGHT::Draw(). Функция визуализации источника света.
- void DrawAxes().Функция отрисовки координатных осей;
- void DrawScene(). Функция отрисовки всей сцены.
3) функции сохранения-зугрузки параметров сцены:
- void SaveScene(char *fn). Сохраняет в файл с именем, заданным аргументом fn, параметры сцены;
- void LoadScene(char *fn). Загружает параметры сцены из файла с именем, заданным аргументом fn;
4) функции построения графического интерфейса:
- void ShowHelp(). Данная функция загружает текст справки из файла и выводит в его во всплывающем окне;
- void InitMainWindow(HINSTANCE hInstance, char *caption, int wdth). Инициализирует главное окно программы. hInstance – экземпляр приложения, caption – заголовок главного окна, width – ширина главного окна;
- void InitPanel(HINSTANCE hInstance). Инициализирует окно панели управления. hInstance – экземпляр приложения;
- void ShowSeparators(int cmd). Функция показа-скрытия разделителей окон проекций. cmd – аргумент, значением которого определяется выполняемое действие (показ или скрытие).
6.8 Описание использованных функций OpenGL
Функции аффинного преобразования в пространстве:
- glRotatef(float a, float x, float y, float z) – поворот. a – угол поворота, x, y, z – координаты вектора, вокруг которого осуществляется вращение;
- glScalef(float x, float y, float z) – масштабирование. x, y и z –коэффициенты масштабирования соответственно по осям Ox, Oy и Oz;
- glTranslatef(float x, float y, float z) – перенос. x, y, z – коеффициенты, задающие расстояние, на которое происходит перемещение по осям Ox, Oy и Oz.
Функции проецирования:
- glViewPort(x,y,width,height) – устанавливает область вывода, заданную переменными x, y, width и height;
- glOrtho(Xmi,Xma,Ymi,Yma,Zmi,Zma) – ортографическая проекция. Xmi, Xma, Ymi и Yma, Zmi, Zma – координаты противолежащих углов параллелепипеда;
Функции для работы с камерой:
- glLookAt(ex,ey,ez,lx,ly,lz,x,y,z) – задает позицию и направление камеры. ex, ey, ez – координаты наблюдателя, lx, ly, lz – точка наблюдения, x, y, z – координаты вектора главной оптической оси камеры.
Функции для работы со светом:
- glLight(light,pname,param) – задает параметры источнику света;
- glLightModelf(pname,param) – задает модель освещения. Pname - имя параметра модели освещения, param – устанавливаемое значение.
Функции удаления невидимых граней:
- glEnable(DEPTH_TEST) – включает тест глубины;
- glDisable(DEPTH_TEST) – выключает тест глубины;
- glDepthFunc(func) – устанавливает функцию глубины;
- glClearDepth(dep) – очищает буфер глубины;
- glDepthRange(Zn,Zf) – задает диапазон глубины.
Функции работы с матрицами:
- glLoadMatrixf(float *matr) – устанавливает в качестве текущей матрицы matr;
- glMultMatrixf(float *matr) – умножает текущую матрицу на matr;
- glLoadIdentity() – делает текущую матрицу единичной;
- glMatrixMode(int matr) – задаёт текущую матрицу.
Функции получения переменных состояния:
- glGetFloatf(float *v) – получение значения переменной типа float;
Функции заания значений переменных состояния булевого типа:
- glEnable(int param) – установка переменной, заданной параметром pname, в true;
- glDisable(int param) – установка переменной, заданной параметром pname, в false.
6.9 Реализация аффинных преобразований
В программе графического моделирования пользователю предоставляется возможность выполнения пяти видов аффинных преобразований: перенос, вращение, масштабирование, сдвиг и отражение. Причём, задание параметров каждого из преобразований производится пользователем. Все аффинные преобразования производятся над всеми примитивами одновременно.
Преобразования переноса, поворота и масштабирования производятся путём вызова функций OpenGL, соответствующих этим преобразованиям (glTranslate, glRotate и glScale), а преобразования отражения и сдвига – путём умножения матрицы модельно-видового преобразования на матрицу соответствующего аффинного преобразования, путём вызова функции OpenGL glMultMatrix.
6.10 Описание структуры программы в виде блок-схемы
Структура работы программы отражена диаграммой состояний на рисунке 6.3.
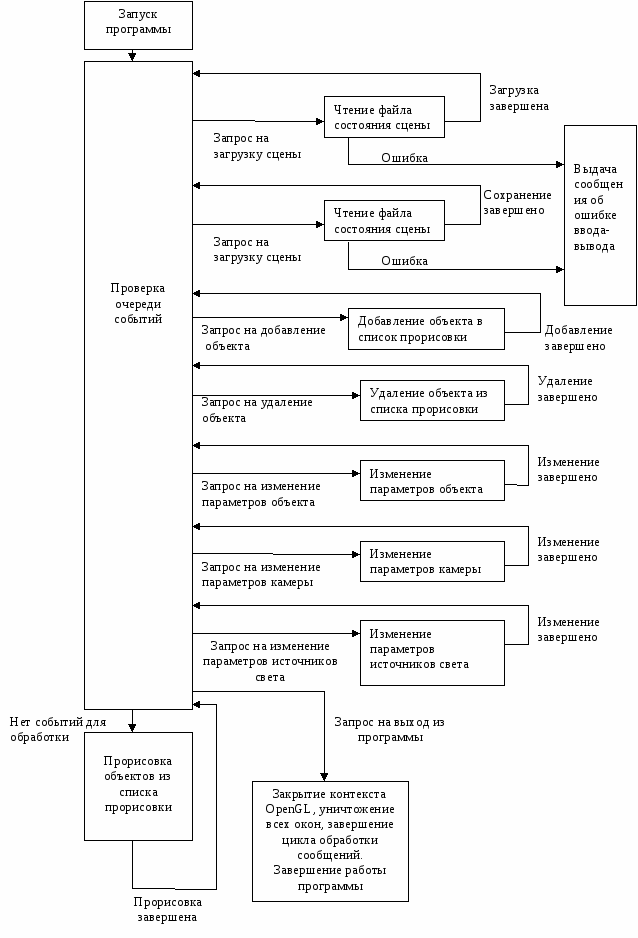
Рисунок 6.3 - Дианрамма состояний
7 ПРОВЕДЕНИЕ ТЕСТОВЫХ ИСПЫТАНИЙ
Проведение тестовых испытаний заключалось в следующем:
- тестирование работы алгоритмов аффинных преобразований над заданной моделью робота-краба и базовых примитивов (см. рис. ,В14,В12);
- тестирование камеры и источников света (см. рис. В.10,В.11,В.13);
- тестирование прорисовки заданных примитивов (см. рис. В.2-В.9);
- тестирование открытия и сохранения сцены;
- сравнение фигуры построенной фигуры (В.14) с ее моделью (А1).
ЗАКЛЮЧЕНИЕ
В результате работы над курсовым проектом была создана интерактивная система трехмерного графического моделирования в пространстве таких объектов как: сфера, полусфера, икосаэдр, призма с треугольным основанием, усеченная пирамида с треугольным основанием, косоугольная призма с треугольным основанием, эллипсоид, косоугольный цилиндр. В ходе реализации проекта были рассмотрены аффинные преобразования как методы выполнения преобразований над объектами в пространстве. Реализована возможность сохранение сцены в файл. Результаты тестирования показали, что программа удовлетворяет предъявленным в постановке задания требованиям.
В дальнейшем КП может быть модернизирован и улучшен в соответствии с нововведенными требованиями.
Список использованной литературы
Курс лекций.
Френсис Хилл. OpenGL. Программирование компьютерной графики. Для профессионалов. – Спб.: Питер, 2002. – 1088 с.: ил.
Девис Т., Нейдер Дж., Шрайнер Д. OpenGL. Руководство по программированию. Юиюлиотека программиста. 4-е издание.- СПб: Питер, 2006 -624с.
Выгодский М.Я. Справочник по высшей математике.– М.: Наука, 1964. – 872с.: ил.
Баяковский Ю.М., Игнатенко А.В. Начальный курс OpenGL.М.: «Планета Знаний», 2007. – 221с.
Шикин А.В. Боресков А.В. Компьютерная графика. Динамика, реалистические изображения. – М.: ДИАЛОГ-МИФИ, 1996. – 288с.
Препарата Ф., Шеймос М. Вычислительная геометрия: Введение: Пер. с англ. - М.: Мир, 1989.-478с.
Эгрон Жерар. Синтез изображений. Базовые алгоритмы.: пер. с франц. А.В.Серединского. М.:Радио и связь, 1993. 216с. библ.-44 , рус.библ.-5.
Rogers, D. 1998. Procedural Element for Computer Graphics. New York: McGraw-Hill;
Yaglom, I.M. 1962 Geometric Transformations. Toronto. Random House.
FAQ по программированию OpenGL http://faqs.org.ru [opengl.txt]
Приложение А
|
|
|
 Скачать 5.65 Mb.
Скачать 5.65 Mb.



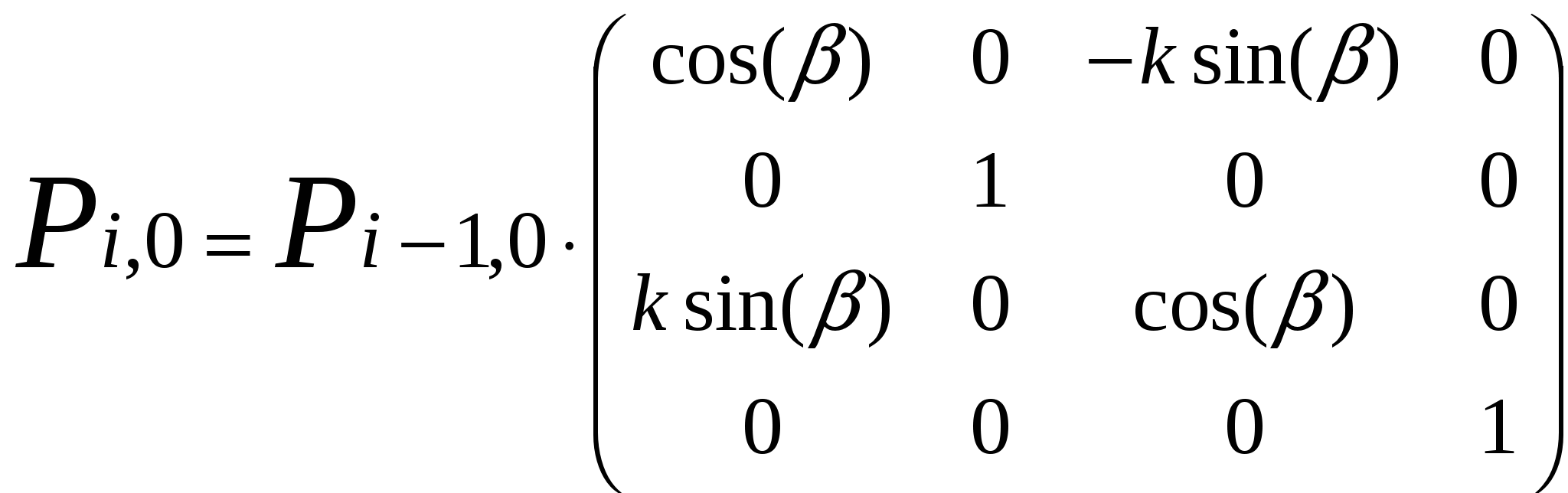





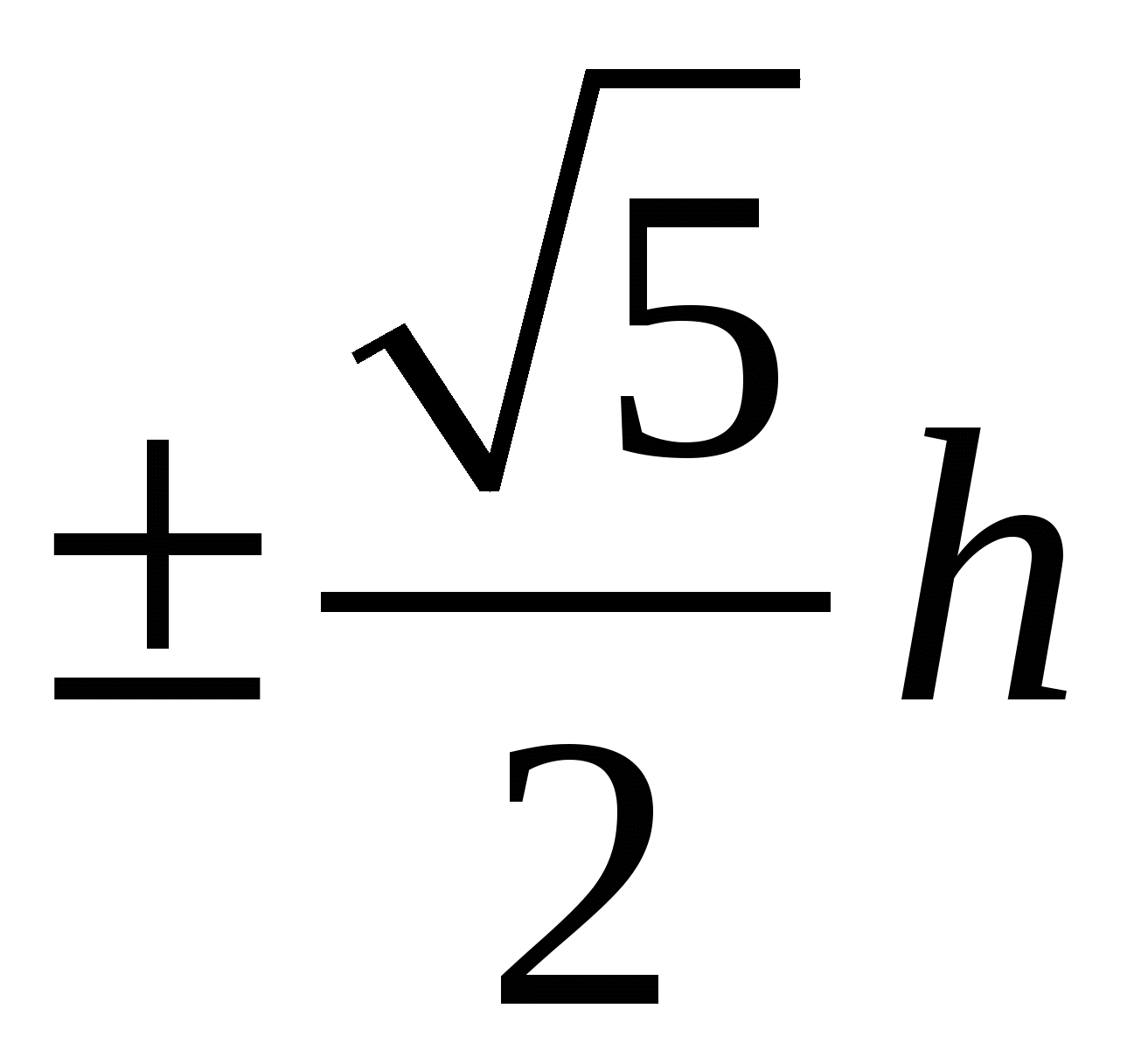 берется окончательная вершина.
берется окончательная вершина.













