Курсовой проект 106 страниц, 42 рисунка, 2 таблицы, 18 фомул, 15 матриц, 4 приложения
 Скачать 5.65 Mb. Скачать 5.65 Mb.
|
Введение В настоящее время применение компьютеров во всех сферах деятельности человека значительно увеличивается. Теперь в какой бы области вы не работали, вам обязательно придется столкнуться с ЭВМ. Одним из бурно развивающихся направлений применения ЭВМ является трёхмерное моделирование. Ещё несколько десятилетий назад никто не мог и представить себе, что с помощью компьютера будет возможно визуально воспроизвести элементы окружающей действительности. В наши дни технологии трёхмерного моделирования позволяют не только увидеть изображение того или иного объекта на экране монитора, но и посмотреть на объект в движении, с разных ракурсов. Более того, изображения получаются настолько реалистичными, что при создании кинофильмов элементы трёхмерного моделирования на ЭВМ великолепно вписываются в съемки реального мира. Компьютерная графика используется во многих отраслях, как научных, то есть при проектировании различных систем или механизмов, так и сфере бизнеса - для создания различного рода рекламных роликов, и индустрии развлечений -для создания разнообразных игр, спецэффектов. Она широко применяется в фильмах, математике, физике. Программа, работающая с трёхмерной графикой, рассчитывает математическую модель изображаемой сцены, преобразуя её к двумерной картине для вывода на плоский монитор, поэтому можно задать закон изменения координат объекта либо самого объекта. Именно такой подход позволяет создавать спецэффекты для фильмов, рисовать произвольные поверхности, изображать движение физической модели. Данный курсовой проект – реализация основных операций, необходимых для работы с объемными изображениями. В нем реализованы три ортогональных проекции и одна изометрическая, основные видовые операции и некоторые операции над объектами. Всё это очень важно для познания методов представления 3D-графики и качественного и эффективного использования её в графическом и геометрическом моделировании в информационных системах. 1 ПОСТАНОВКА ЗАДАЧИ 1.1 Цель создания Целью создания проекта является приобретение практических навыков трёхмерного графического моделирования, а так же разработка системы моделирования трехмерных сцен поддерживающей параметрические объекты и позволяющей производить простейшие преобразования над ними: перемещение, вращение, масштабирование, отражение, сдвиг. 1.2 Область применения Данный проект может быть использован для демонстрации работы основных алгоритмов построения и визуализации трёхмерных моделей простейших геометрических объектов. 1.3 Актуальность разработки Задача построения трёхмерных моделей решалась не раз. Примером этому могут служить такие известные пакеты как 3D Studio Max, Maya и AutoCAD. Безусловно, они предоставляют гораздо более широкий круг функциональных возможностей, чем данный проект, но в то же время для использования только в демонстрационных целях они занимают слишком много места на жестком диске и ресурсов системы. 1.4 Постановка задачи Основной задачей разработки является разработка и реализация с помощью библиотеки OpenGL системы трехмерного графического моделирования, поддерживающей несколько типов параметрических объектов и видов проецирования, позволяющей просматривать композиции данных объектов с разных ракурсов и проводить их визуализацию с использованием различных методов. Систему трехмерного графического моделирования должна обладать следующей функциональностью:
1.5 Сравнительный анализ существующих графических библиотек На современном этапе развития систем по обработке компьютерной графики существует несколько методов по визуализации на экране компьютера графических объектов. Рассмотрим три основных метода: программный, использование библиотеки OpenGL и библиотеки DirectX. 1.5.1 Библиотека Microsoft DirectX Библиотека Microsoft DirectX является наиболее динамично развивающейся и полнофункциональной. Ее преимущества: - поддержка со стороны операционной системы Microsoft Windows; - набор методов DirectInput, DirectPlay, DirectSound, DirectDraw, позволяющих не только выводить графику, но и обрабатывать ввод данных со стороны пользователя, обрабатывать звуковую информацию, а также производить обмен данными по компьютерной сети. - Основными недостатками этой библиотеки являются: моноплатформенность; - не очень сильная аппаратная поддержка со стороны графических процессоров; - абсолютная коммерциализация всех продуктов корпорации Microsoft. 1.5.2 Пакет графического моделирования OpenGL Библиотека OpenGL представляет собой интерфейс программирования трехмерной графики. Единицей информации является вершина, из них состоят более сложные объекты. Программист создает вершины, указывает как их соединять (линиями или многоугольниками), устанавливает координаты и параметры камеры и ламп, а библиотека OpenGL берет на себя работу создания изображения на экране.. Используя OpenGL легко создать трехмерные поверхности, наложить на них текстуры, осветить источниками света, сделать эффект тумана, прозрачности, смешивания цветов, а также наложить трафарет, передвигать объекты сцены, лампы и камеры по заданным траекториям, сделав, тем самым, анимацию. Для работы с устройствами ввода, такими как клавиатура или мышь, можно задействовать функции конкретной операционной системы, под которую пишется программа, или воспользоваться надстройками над OpenGL, такими как библиотеки GLUT или GLAUX. В различных видеокартах по разному реализованы функции по обработке данных. Часть из них лучше работает с интерфейсом OpenGL, часть – DirectX. Большинство производителей видеокарт обеспечивают аппаратную поддержку как можно большего числа функций. Но, так как спецификация библиотеки OpenGL абсолютно открыта, то реализация чисто OpenGL-алгоритмов часто оказывается лучше, чем алгоритмов DirectX. 2 ОБОСНОВАНИЕ ИСПОЛЬЗОВАНИЯ OPENGL Графический стандарт OpenGL, разработан и утвержден в 1992 году девятью ведущими фирмами, среди которых Digital Equipment Corporation, Evans & Sutherland, Hewlett–Packard Co., IBM Corp., Intel Corp., Intergraph Corp., Silicon Graphics, Inc., Sun Microsystems Inc. В основу стандарта была положена библиотека IRIS GL, разработанная Silicon Graphics. Это достаточно простая в изучении и использовании графическая система, обладающая при этом поразительно широкими возможностями. Вот только некоторые из ее достоинств:- Стабильность. OpenGL устоявшийся стандарт, действующий уже девятнадцать лет. Все вносимые в него изменения предварительно анонсируются и реализуются таким образом, чтобы гарантировать нормальную работу уже написанного программного обеспечения. - Надежность. Все приложения, использующие OpenGL, гарантируют одинаковый визуальный результат вне зависимости от используемого оборудования и операционной системы. - Переносимость. Для запуска OpenGL-приложения необходима лишь его компиляция под конкретную платформу без изменения OpegGL-части кода. - Простота использования.OpenGL хорошо структурирована. Ее драйверы включают информацию об основном оборудовании, освобождая разработчика приложения от необходимости проектирования для специфических особенностей графических устройств. Команды OpenGL обеспечивают необходимый баланс между необходимыми функциональными возможностями и гибкостью. Каждая команда OpenGL строго придерживается опубликованной спецификации, сохраняя драгоценный цикл разработки, который теряется при работе с другим, менее удачно спроектированным интерфейсом. Альтернативой библиотеке OpenGL являются разработанные компанией Microsoft библиотеки DirectShow и DirectDraw, входящие в состав DirectX. В отличие от OpenGL DirectX не является свободно распространяемой библиотекой и не обеспечивает переносимости приложений, т.к. разработана исключительно для операционных систем Microsoft Windows. 3 АНАЛИЗ ГРАФИЧЕСКИХ И ГЕОМЕТРИЧЕСКИХ МЕТОДОВ 3.1 Системы координат 3.1.1 Декартова система координат Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат в пространстве. Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 3.1). 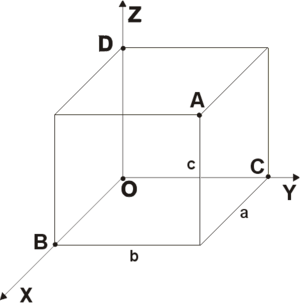 Рисунок 3.1. Декартова система координат Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(x,y,z). 3.1.2 Векторная система координат Для векторной системы координат, как и для декартовой, характерно задание прямых, направлений и единичных отрезков, но в отличие от декартовой, в ней устанавливает взаимно однозначное соответствие между векторами пространства и упорядоченными тройками действительных чисел, а не между числами и точкой. Любой вектор р заданный тройкой чисел представляет собой направленный отрезок исходящий из точки O в точку Р. Векторная система координат показана на рисунке 3.2. 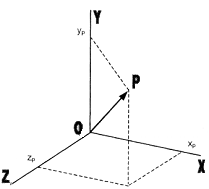 Рисунок 3.2 - Векторная система координат 3.1.3. Аффинная система координат Аффинная система координат является объединением декартовой и векторной систем координат и устанавливает взаимно однозначное соответствие между точками, векторами пространства и упорядоченными тройками действительных чисел. 3.1.4 Однородные координаты точки Для n-мерного пространства в однородных координатах вершины всегда задаются n+1 координатами. Основное удобство применения однородных координат заключается в том, что с их помощью все виды преобразований координат могут быть представлены в единой форме. Они были введены в геометрии и впоследствии использованы в графике. В однородных координатах положение точки Р(х, у, z) записывается как P(W*x, W*y, W*z, W) или P(X, Y, Z, W), для любого масштабного множителя, причем трехмерные декартовы координаты легко определяются: х = X/W; у = Y/W; z = Z/W (3.1) То есть привычная для нас ортогональная система координат получается как проекция однородной системы на плоскость W = 1. Таким образом для преобразования точки из обычных координат в однородные нужно добавить компоненту равную 1 и умножить все компоненты на любое вещественное число. Для преобразования точки из однородных координат в обычные координаты разделите все компоненты на последний компонент и отбросьте его. 3.2 Аффинные преобразования в пространстве Аффинные преобразования - это комбинация линейных преобразований, переводящие параллельные прямые в параллельные, скрещивающиеся в скрещивающиеся и сохраняющие величину отношения длин отрезков параллельных прямых. Они допускают компактное матричное представление. Аффинные преобразования в однородных координатах описываются матрицами 4*4. Пусть есть некоторая точка P и некоторое аффинное преобразование, которому соответствует матрица М. Тогда результирующая точка P’ для данного аффинного преобразования и данной точки может быть вычислена по формуле: Используя матрицы аффинных преобразований, получают координаты точки после преобразования по координатам исходной точки. Используя матрицу, обратную матрице преобразования, по координатам результирующей точки получают координаты исходной точки. Композиция нескольких аффинных преобразований в одно представляется в матричном виде как произведение матриц составляющих сложного преобразования в порядке их применения к точке. Основными аффинными преобразованиями принято считать преобразования переноса, поворота и масштабирования. Также отдельно выделяют преобразование отражения и сдвига. 3.2.1 Преобразования переноса Перенос точки Р на вектор (x,y,z) осуществляется при помощи умножения вектора координат точки Р на матрицу переноса. Матрица переноса имеет вид: 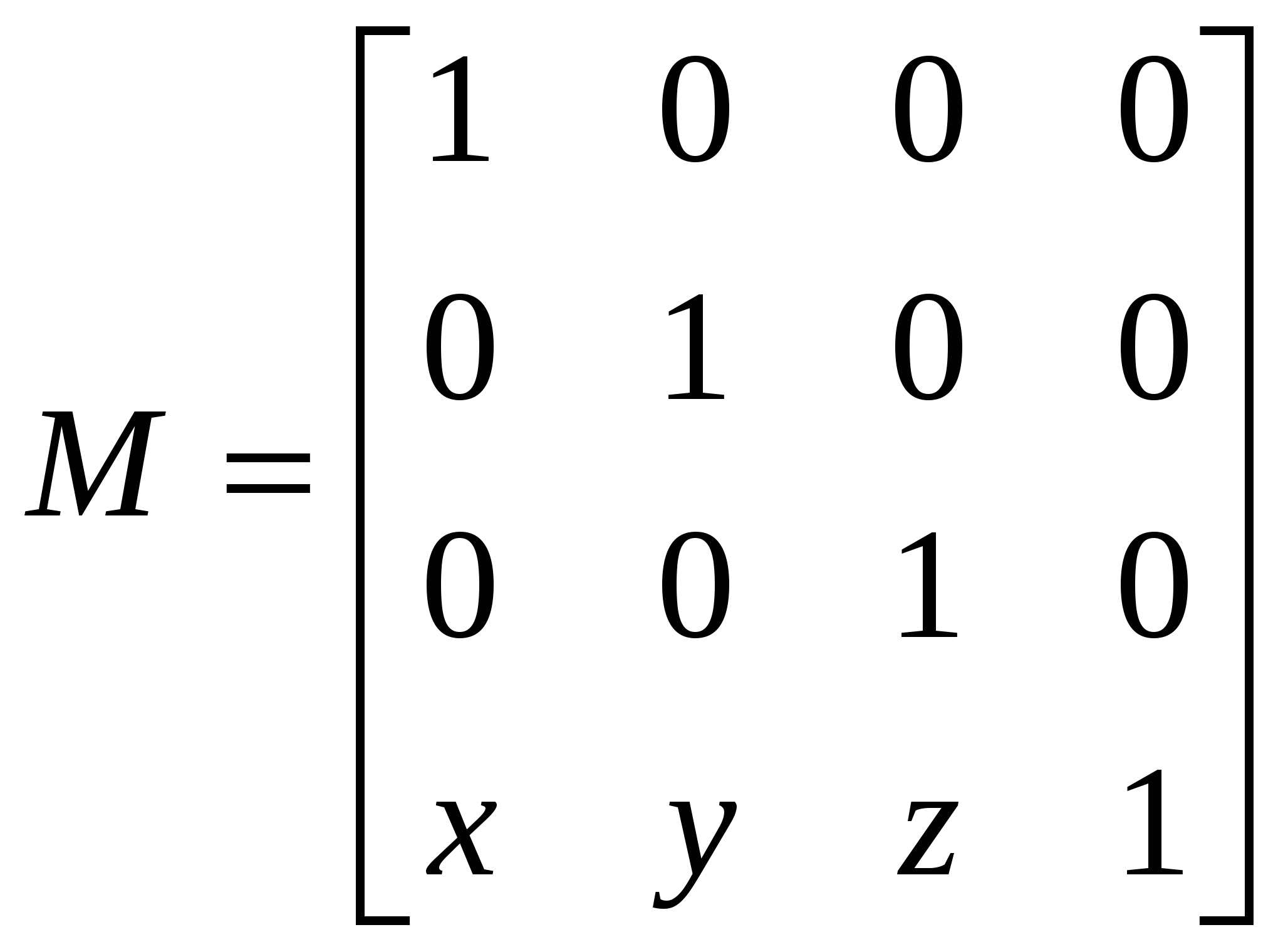 (3.1) (3.1)Перенос точки Р в точку Р’ показан на рисунке 3.3. 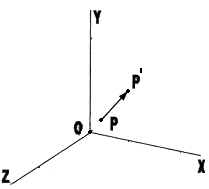 Рисунок 3.3 – Перенос точки Р в точку Р’ 3.2.2 Преобразования поворота Одной из основных операций аффинных преобразований является поворот фигуры относительно заданной точки на некоторый угол. Осуществляется он при помощи умножения координат фигуры на матрицу поворота. Матрицы поворота вокруг заданных осей на угол r имеют вид: Вокруг оси абсцисс: 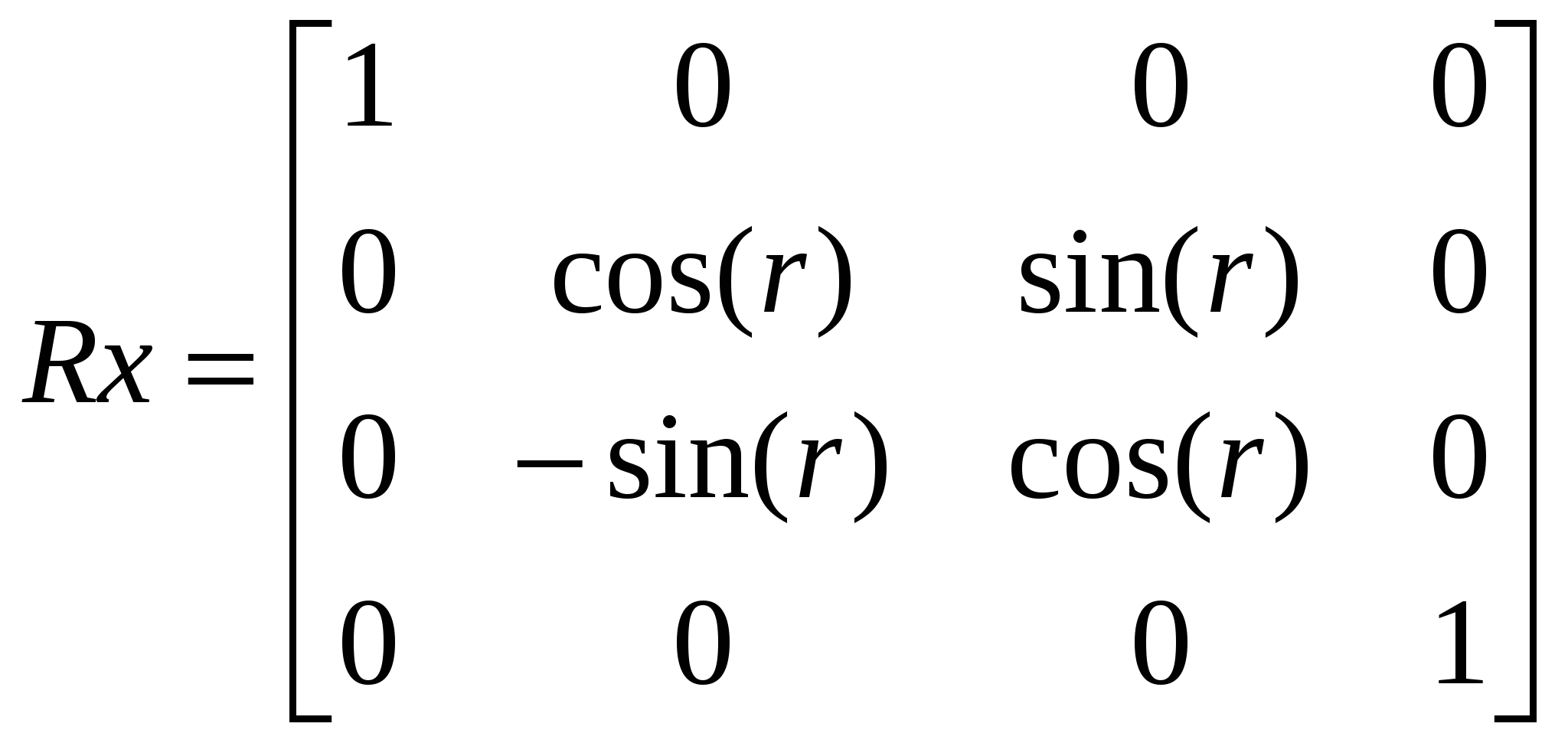 (3.2) (3.2)Вокруг оси ординат: 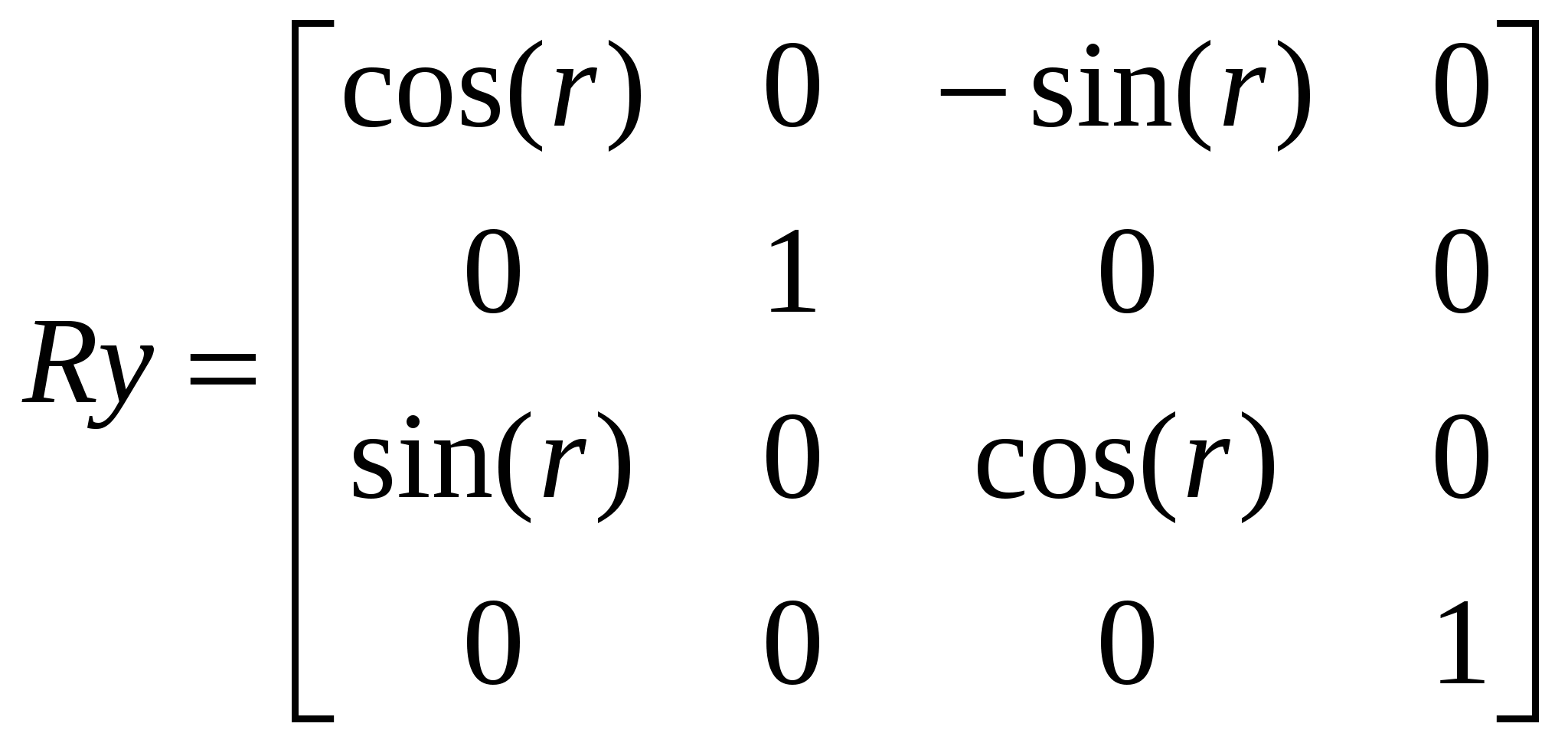 (3.3) (3.3)Вокруг оси аппликат: 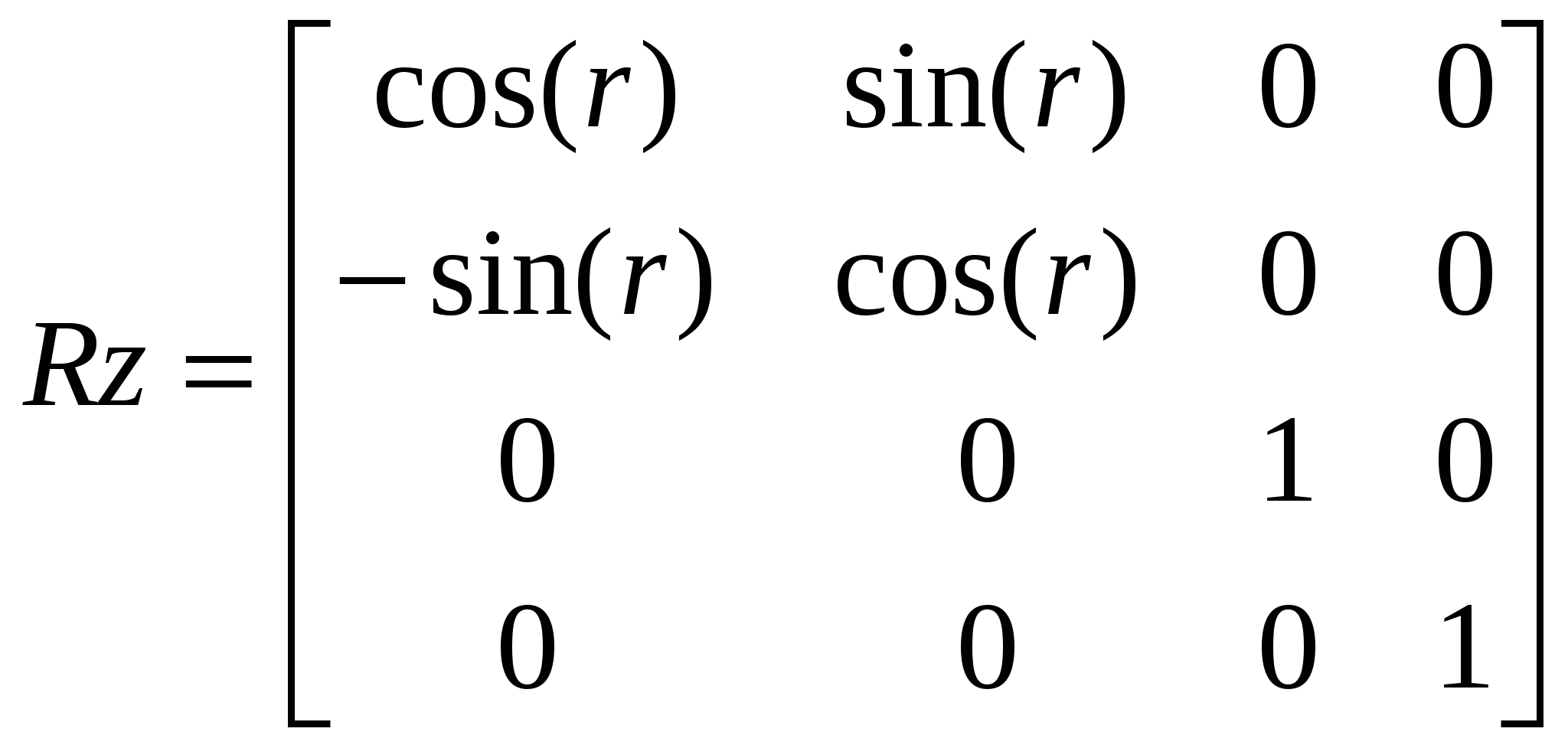 (3.4) (3.4)На рисунке 3.4 приведены три основных положительных поворота. 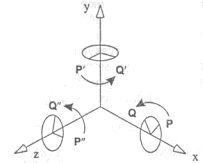 Рисунок 3.4 – Положительные повороты вокруг осей 3.2.3 Преобразования масштаба Масштабирование изменяет размер фигуры и использует три масштабных множителя — Sx , Sy и Sz для координат x, у и zсоответственно. Более строго такой способ масштабирования называется масштабированием относительно начала отсчета, поскольку каждая точка передвигается в Sx раз дальше от начала отсчета в направлении х, в Syраз дальше от начала отсчета в направлении y и в Sz раз дальше от начала отсчета в направлении z. Матрица масштабирования имеет вид: 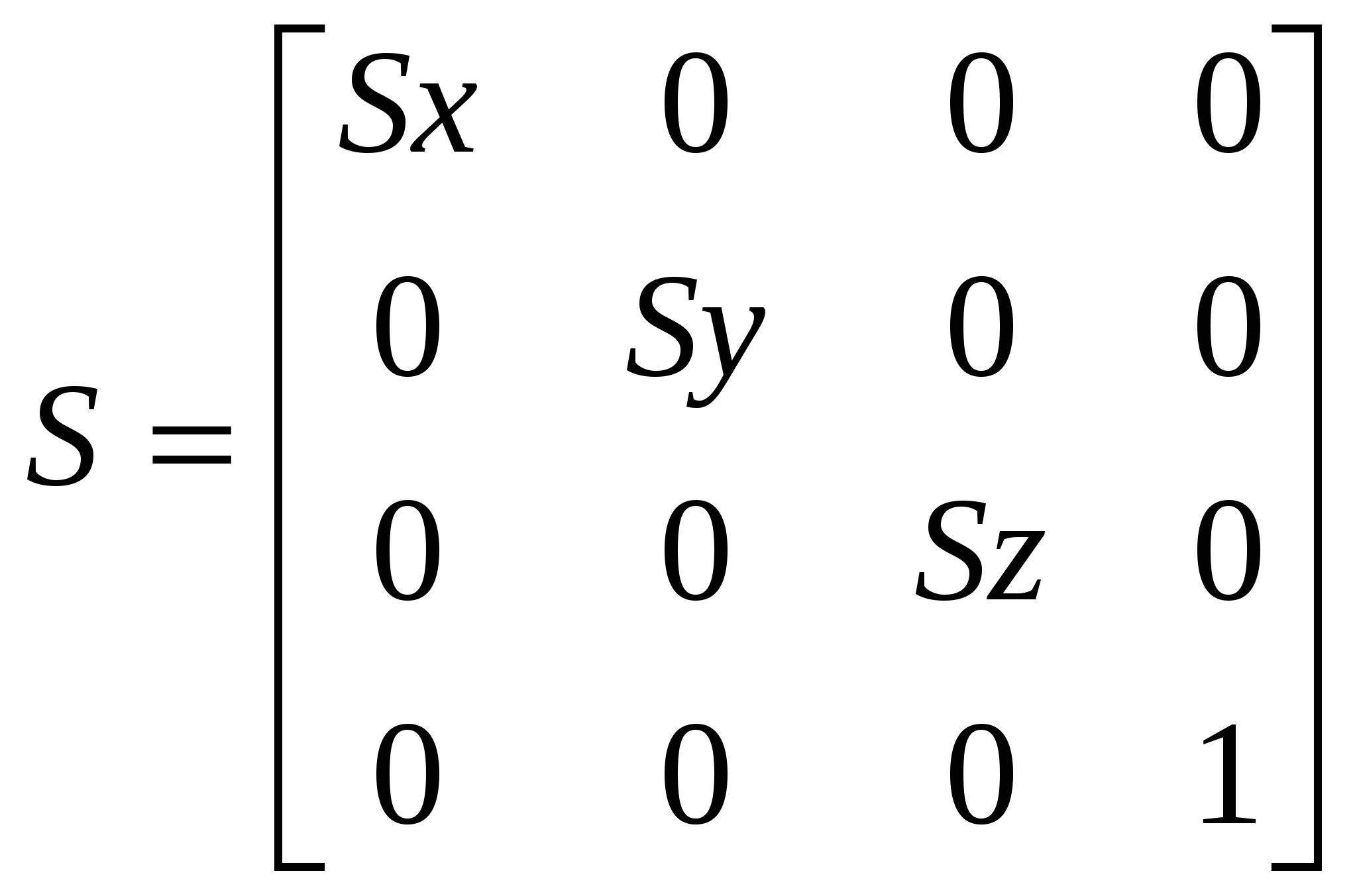 ( 3.5) ( 3.5) 3.2.4 Преобразования отражения Если масштабный множитель отрицателен и равен 1, то происходит отражение относительно координатных плоскостей. Матрицы отражения относительно плоскостей YОZ, XОZ и XОY имеют вид: 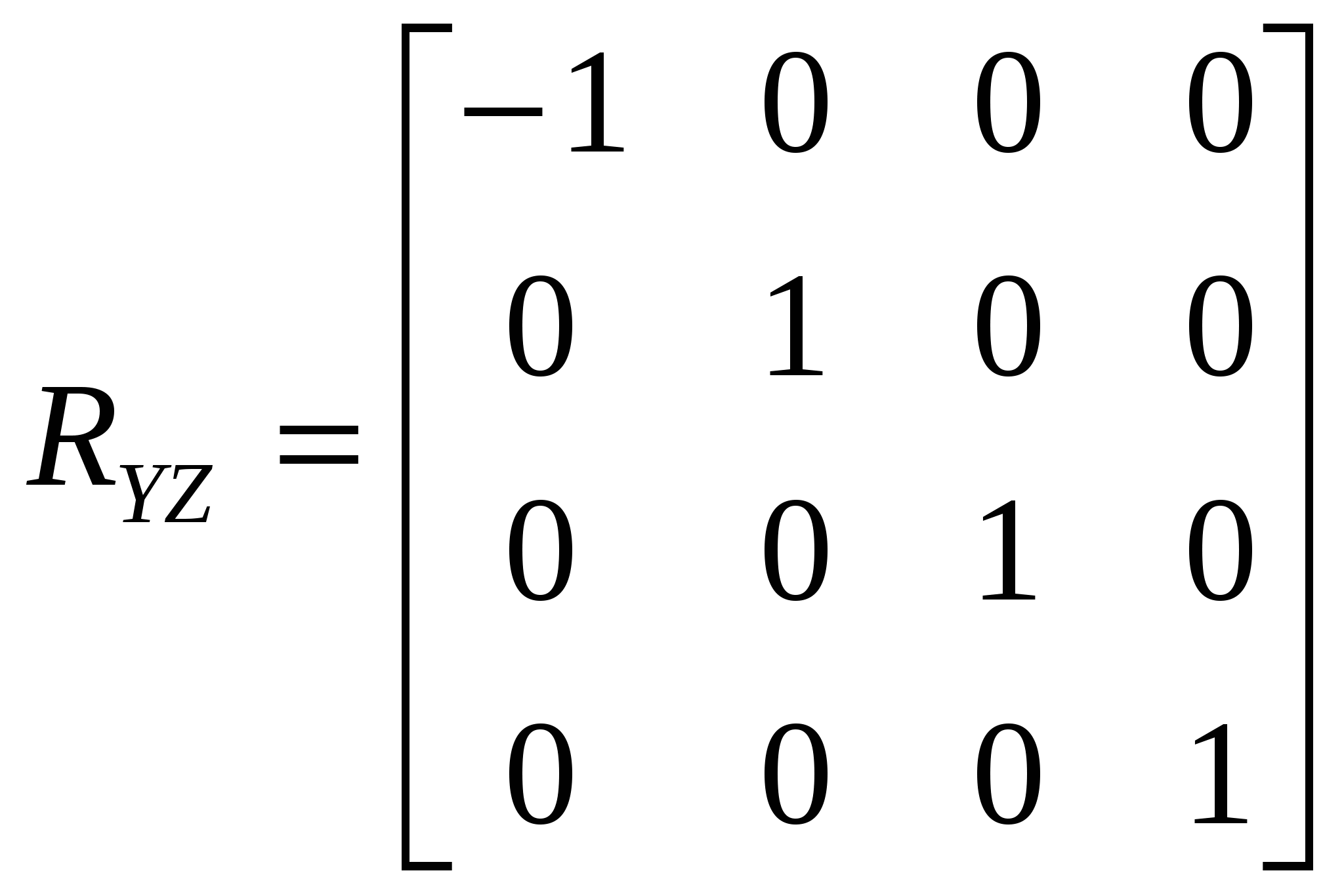 (3.6); (3.6); 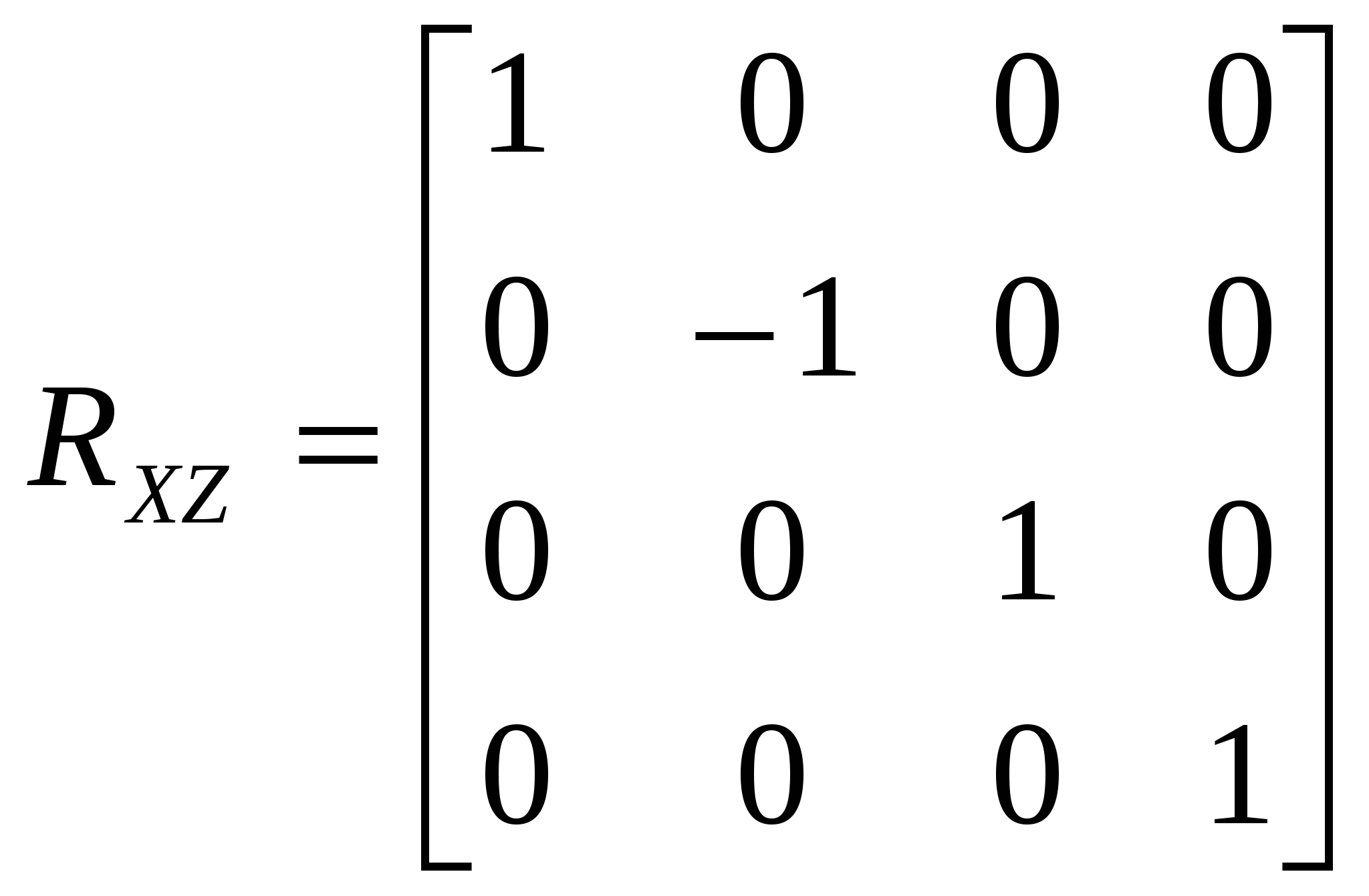 (3.7); (3.7);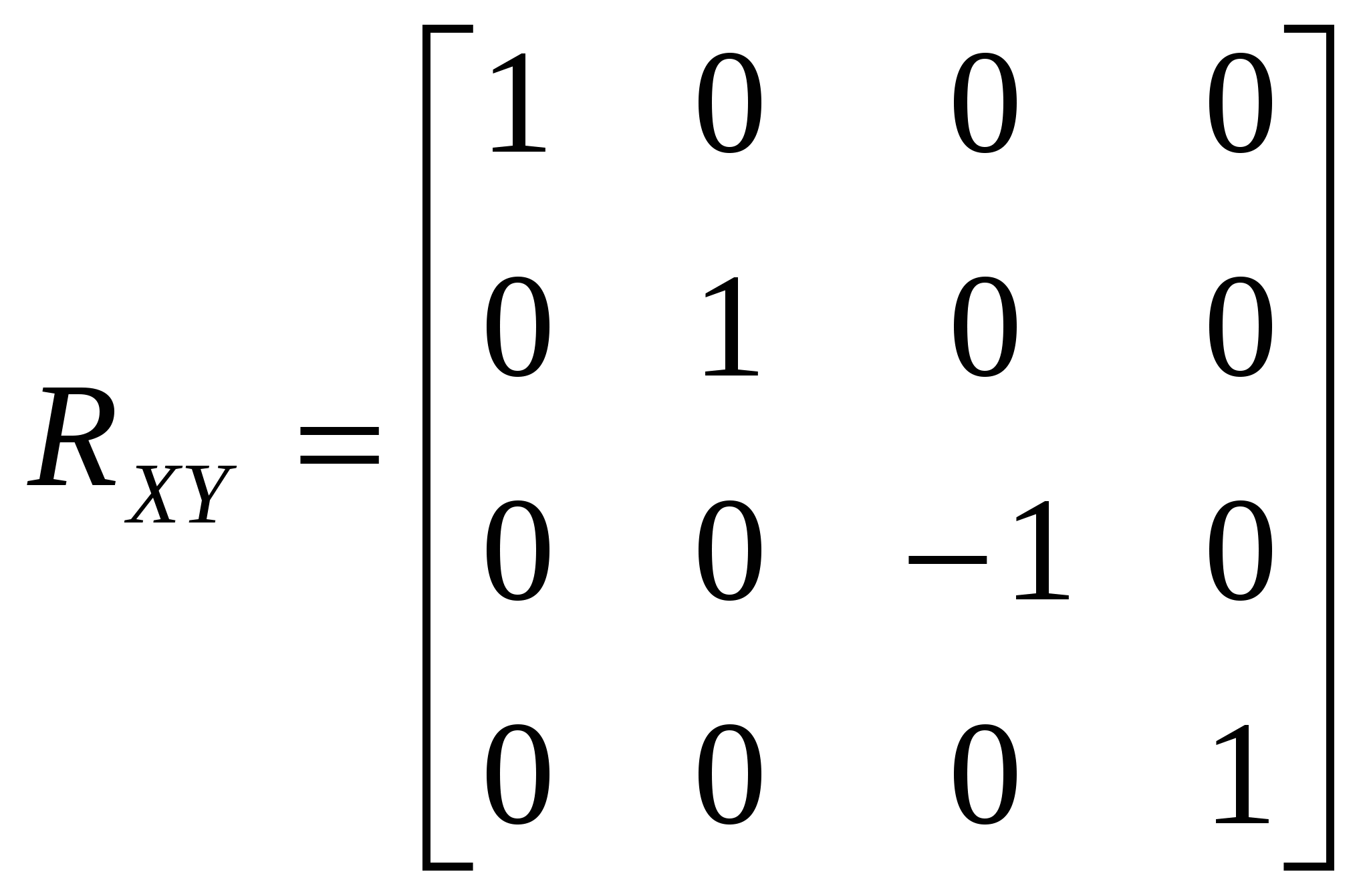 (3.8); (3.8);На рисунке 3.5 приведен пример отражения точки А относительно плоскости XОY. 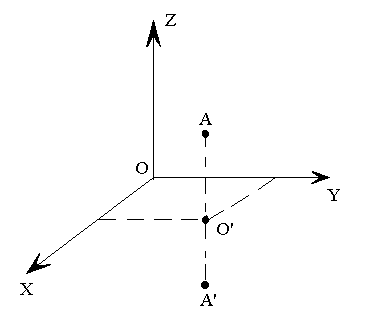 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

