билеты геометрия. Билеты аналитическая геометрия. 1. Декартовы координаты на прямой
 Скачать 1.74 Mb.
|
|
Декартовы координаты на прямой. Направленный отрезок. 1. Декартовы координаты на прямой Прямая, на которой выбрано положительное направление, называется осью.  Ось, с выбранным началом координат и масштабом единицы, называется числовой осью. Направленным отрезком, называется отрезок на оси, для которого указана, какая из его ограниченных точек является началом, а какая концом. 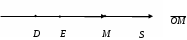 Каждому направленному отрезку на оси ставится определенная числовая характеристика – ее величина. Определение: Величиной направленного отрезка AB, называется число, равное длине отрезка AB, взятое со знаком плюс, если направление отрезка AB совпадает с положительным направлением оси и со знаком минус, если направление AB противоположно направлению оси. АВ – величина  - длина Если начало и конец направленного отрезка совпадают, то такой отрезок называется нулевым,  .Замечание: 1) нулевой отрезок не определяет направление; 2) величина нулевого отрезка равна нулю. Предложение: Необходимым и достаточным условием равенства двух направленных отрезков на данной оси является равенство величин этих отрезков,  и  - противоположны друг другу.При любом расположении точек A, B и C на оси величины отрезков  связаны соотношением AB+BC=AC, которое называется основным тождеством.  П  усть дана произвольная прямая а. На прямой а выберем определенное направление и некоторую точку О (начало координат). Укажем единицу масштаба.Декартовой координатой точки Рассмотрим произвольную точку М на прямой. Определение:Декартовой координатой xточки М на прямой называется величина направленного отрезка  и обозначается  , x=OM.Символ M(x) означает, что точка М имеет координату x. Пусть  и  - две произвольные точки прямой а.Теорема:Каковы бы ни были две точки и , всегда имеет место равенство:  .Чтобы получить величину отрезка оси, нужно от координаты его конца отнять координату начала. Длина  2.Декартовы координаты на плоскости. Определение: Упорядоченная тройка точек O,  принадлежащие одной плоскости и не лежащие на одной прямой называется аффинной системой координат.О  бозначения.  . О – начало координат. Две взаимно перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют прямоугольную декартовую систему координат на плоскости.Точка пересечения осей называется началом координат, а сами оси – координатными осями. 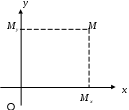  - ось абсцисс. - ось ординат.M - произвольная точка на плоскости.  - проекции соответственно на оси  . Определение: Декартовыми прямоугольными координатами x и y точки М наплоскости, называются соответственно величины направленных отрезков 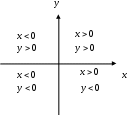 и  .  . Декартовы координаты x и y точки М называются соответственно ее абсциссой и ординтой. Обозначается через М(x,y). К  оординатные оси разбивают плоскость на четыре квадранты (координатные четверти).3.Декартовы координаты в пространстве Определение: Аффинной системой координат в пространстве, называется упорядоченная четверка точек общего положения (никакие четыре не лежат в одной плоскости). 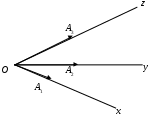   Три взаимно перпендикулярные оси в пространстве с общим началом О и одинаковой масштабной единицей, образуют декартовую прямоугольную систему координат в пространстве. Ось 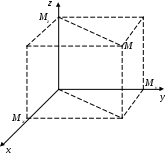называется осью абсцисс, ось осью ординат, ось  называется осью аппликат.  Пусть  - проекции произвольной точки М на координатные оси , и соответственно.Определение: Декартовыми прямоугольными координатами точки М в пространственазываются соответственно величины направленных отрезков  .  ,  ,  . Обозначают через M(x,y,z). Три координатные оси разбивают пространство на 8 четвертей или октанты. 4.. Расстояние между двумя точками. a) на числовой оси. Пусть нам дана числовая ось.  - произвольные точки на оси. - величина.  - длина.б) на плоскости ПДСК. Пусть нам задана прямоугольная декартовая система координат. 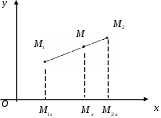  ,  ,  . .   - расстояние между двумя точками на плоскости.в) в пространстве:  - расстояние между двумя точками в пространстве.II. Деление отрезка в данном отношении: а) на прямой. Пусть задана числовая прямая и пусть даны три точки, принадлежащие ей. 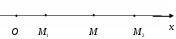 Определение: Число А равное отношению величины отрезков  называется простым отношением трех точек и обозначается  , где  - базисные (основные) точки, M – делящая точка.Если: 1) А>0, то  2) А<0, то  3) А=1, то M - середина отрезка 4) А =-1, то М -не существует. 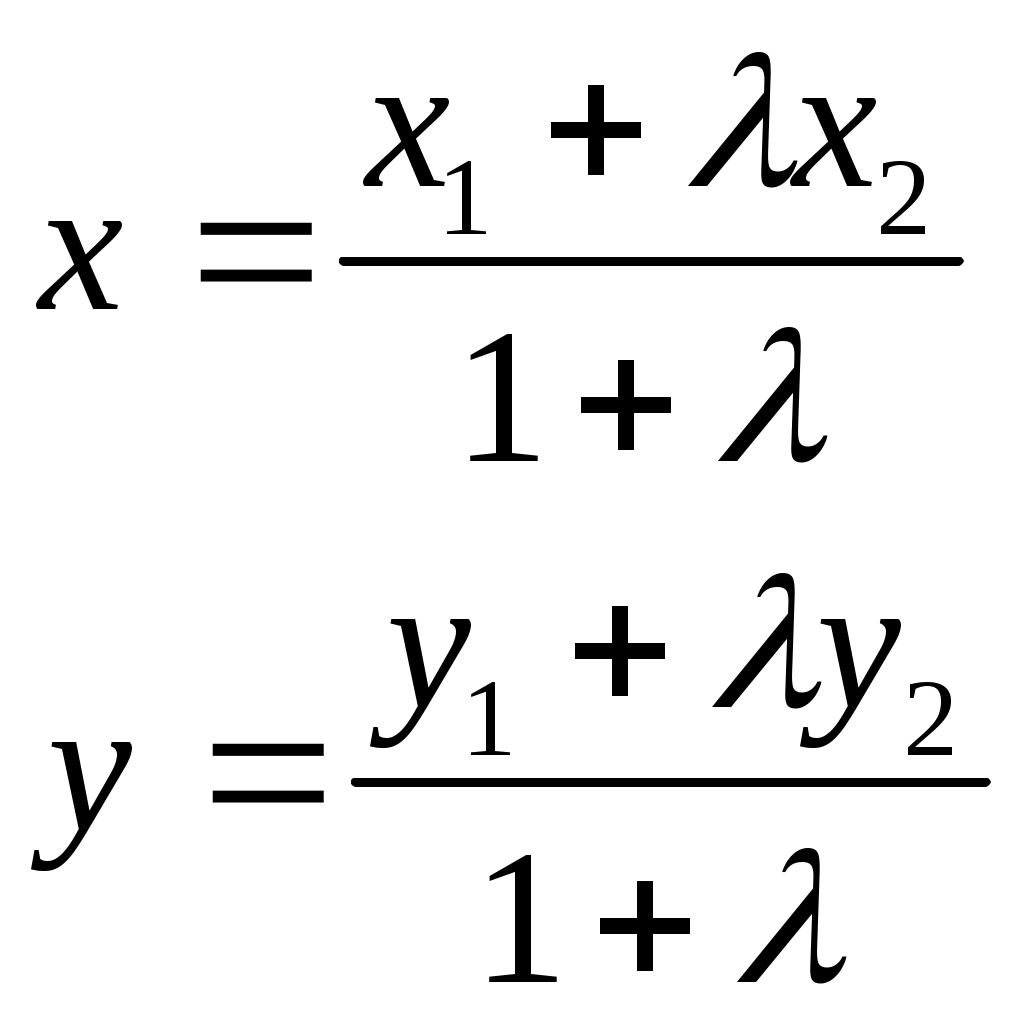 - формулы деления отрезка в данном отношении.Если  ,  - середина.в) в пространстве:  ,  ,  - формулы деления отрезка в данном отношении.5.Полярные, цилиндрические и сферические координаты 1. Полярные координаты Полярные координаты на плоскости вводятся следующим образом. Выберем на плоскости некоторую точкуO(полюс) и некоторый выходящий из него луч Ox,укажем единицу масштаба. Определение: Полярными координатами точки M называются два числа  , где  - полярный радиус,  - полярный угол, угол на который нужно повернуть против часовой стрелки луч Oxдо совмещения с лучом  .Обозначение 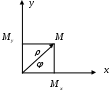 - точка М с полярными координатами  и . Для того чтобы соответствие между отличными от полюса точками плоскости и парами полярных координат  было взаимно однозначным, считают, что изменяются в следующих границах:  ,   Предположим, что начало декартовой прямоугольной системы координат находится в полюсе, а ось Оx совпадает с полярной осью. M(x,y) – декартовы координаты, - полярные координаты.Тогда  - связь между полярными координатами точки и ее декартовыми координатами. ,  . Цилиндрические координаты Цилиндрические координаты в пространстве вводятся следующим образом. Выберем на фиксированной плоскости 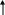 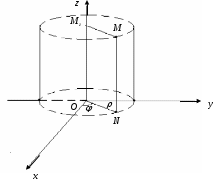некоторую точку О и выходящий из него луч Оx. Рассмотрим Oz, проходящую через точку О перпендикулярно плоскости . Пусть М – любая точка пространства, N – проекция этой точки на плоскость . - проекция М на ось Oz.   Определение: Цилиндрическими координатами точки М называются три числа  , где  - являются полярными координатами точки N d плокскоти относительно полюса О и полярной оси Ox, а число z – есть величина отрезка  . Точку М с цилиндрическими координатами обозначают  . связь между цилиндрическими и декартовыми координатами точки.Сферические координаты Для введения сферических координат в пространстве рассмотрим три взаимно перпендикулярные оси Ox, Oy, Oz c общим началом О. Пусть М – любая точка пространства, N – ее проекция на плоскость Oxy. ,  - угол, который образует направленный отрезок  с осью Oz, - угол, на который нужно повернуть против часовой стрелки ось Oxдо совмещения с лучом  . называются широтой и долготой.Сферическими координатами точки М называются три числа 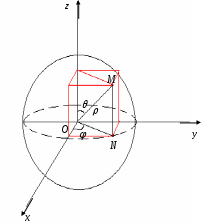 . Для того чтобы соответствие между точками пространства и тройками сферических координат  было взаимно однозначным, считают, что изменяются в следующих границах: , . Координата по определению заключена между 0 и .   связь между сферичекскими и декартовыми координатами точки. 6.Понятие вектора и линейные операции над векторами Определение: Геометрическим вектором, или просто вектором называют направленный отрезок. Обозначается  , где А начало, В конец вектора. Начало вектора называется точкой его приложения. Определение: Число, равное длине вектора называется его модулем. Модуль вектораа обозначается символом  .Определение: Если  , то вектора называется единичным. Определение: Единичный вектор, имеющий одинаковое направление с данным векторома, называется ортом вектораа и обозначается символом  .  .Определение: Вектор называется нулевым, если начало и конец его совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Определение: Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Определение: Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными. Линейными операциями принято называть операцию сложения векторов и операцию умножения векторов на вещественные числа. Определение: Суммой 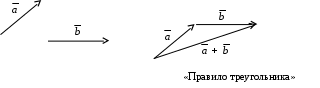 двух векторова иbназывается вектор, идущий из начала вектораа в конец вектора b при условии, что векторb приложен к концу вектора а. Если векторыа иbприведены к общему началу и на них построен параллелограмм , то сумма 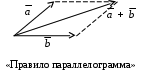, есть вектор совпадающий с диагональю этого параллелограмма, идущей из общего началаа иb.  Свойства сложения векторов: 1.  (переместительное свойство, коммутативность);2.  (сочетательное свойство, ассоциативность);3.Существует нулевой вектор 0такой, что  для любого вектора;4. Для каждого вектораа существует противоположный ему вектор  такой, что  .Определение: Разностью 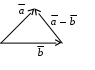 вектораа и вектораb называется такой векторс, который в сумме с векторомb, дает вектора. Правило построения разности Если два вектораа иb приведены к общему началу, то разность их есть вектор идущий из концаb (вычитаемого) к концуа (уменьшаемого).Определение: Произведением  вектораа на вещественное число называется вектор, модуль которого равен произведению модуля вектораа на модуль числа .  . Он параллелен векторуа или лежит с ним на одной прямой и направлен также, как вектора, если  , и противоположно векторуа, если  .Геометрический смысл операции умножения вектора на число: при умножении вектораа на число вектора «растягивается» в если раз.  Свойства: 5.  (распределительное свойство числового сомножителя относительно суммы векторов);6.  (распределительное свойство векторного сомножителя относительно суммы чисел);7.  (сочетательное свойство числовых сомножителей).2. Линейная зависимость векторов Теорема 1: Если векторыа иb коллинеарны и  , то существует единственное число такое, что  . Теорема 2: Если векторыа,b ис компланарны, а векторы а,b не коллинеарны, то существует единственные числа и такие, что  .Определение: Система векторов  называется линейно зависимой, если существуют числа  среди которых хотя бы одно отлично от нуля, и такие что  (1).Если же равенство (1) справедливо при  , то система векторов называется линейно независимой.Теорема 3: Система векторова,bлинейно зависима тогда и только тогда, когда эти векторы коллинеарны. Определение: Множество V называется векторным пространством, если на V определена операция сложения векторов и умножения вектора на число. Определение: Базисом векторного пространства называется такая система векторов, которая задана в определенном порядке и удовлетворяет условиям: а) система линейно не зависима; б) любой вектор пространства является линейной комбинацией данной системы векторов. 6. Проекция вектора на ось Определение: Проекцией вектора на ось и называется число, равное величине отрезка  оси и, где А1 – является проекцией точки А на ось и, В1 – является проекцией точки В на ось и.Обозначение  .Теорема: Проекция вектораа на ось и равна длине вектораа, умноженной на cos угла наклона вектораа к оси и. . (2)7. . Разложение вектора на компоненты. Координаты вектора. Направляющие косинусы. Определение: Тройка векторовi,j,k называется координатным базисом, если эти векторы удовлетворяют следующим условиям: векторi лежит на оси Ох,j – на оси Оу,k – на оси Oz. каждый из векторовi,j,k направлен на своей оси в положительную сторону. в 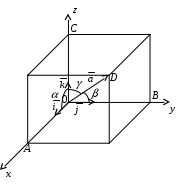 екторыi,j,k – единичные, т.е.  .Каким бы ни был вектора, он всегда может быть разложен по базисуi,j,k, т.е. может быть представлен в виде  .Коэффициенты этого разложения являются координатами вектораа. Символически обозначается  .ОА = Х; ОВ = Y; ОС = Z. OD – диагональ параллелепипеда.  . (3), , - углы наклона вектораа к осям OX, OY, OZ. Тогда  ,  ,  (из (2) см. формулу проекцию вектора на ось).cos, cos, cos - называются направляющими косинусами вектораа. Из формулы (3) вытекает  .Сумма квадратов направляющих косинусов любого вектора равна единице. Вектора однозначно определяется заданием его длины и трех направляющих косинусов. Если  и  , , .Признаком коллинеарности двух векторов является пропорциональность их координат.  то  .8.Скалярное произведение векторов Определение: Скалярным произведением двух векторов называется число равное произведению длин этих векторов на косинус угла между ними.  Геометрические свойства скалярного произведения Теорема1: Необходимым и достаточным условием ортогональностей двух векторов является равенство нулю их скалярного произведения. Теорема 2: Два вектораа иb составляют острый (тупой) угол, если их скалярное произведение положительно (отрицательно).Алгебраические свойства скалярного произведения 1.  (коммутативность)2.  (ассоциативнсть числового сомножителя)3.  (дистрибутивность)4.  , если вектора не нулевой вектор. если вектора нулевой вектор .10. Выражение скалярного произведения в декартовых координатах. Теорема : Если векторыа иb определены своими декартовыми координатами, то скалярное произведение  .Следствие1 : Необходимым и достаточным условием ортогональности двух векторов является равенство:  Следствие2: Угол между векторамиа иbопределяется по следующей формуле: 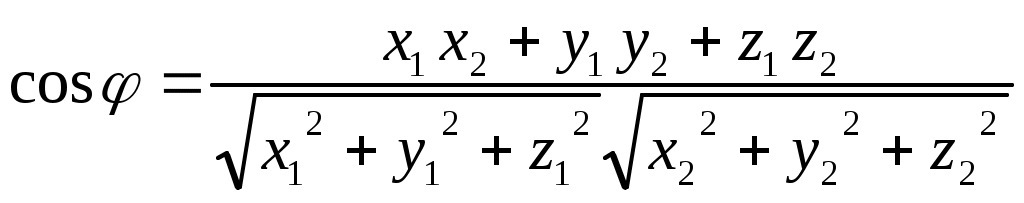 11. Векторное произведение векторов. Алгебраические и геометрические свойства. Определение: Пусть векторыа,b,с некомпланарные, тогда векторным произведением называется вектор обозначаемый символом  и определяемый следующими тремя условиями:1. Модуль векторного произведения равен произведению длин векторова иb на синус угла между ними  .2. Вектор перпендикулярен каждому из векторова иb. Вектор перпендикулярен векторуа, вектор перпендикулярен векторуb.3. Направление векторного произведения соответствует правилу правой руки оно означает: если векторыа,b и 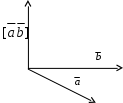приведены к общему началу, то должен быть направлен как средний палец правой руки, большой палец направлен по векторуа, а указательный по векторуb.  Геометрические свойства векторного произведения Теорема1: Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения. Теорема2: Модуль векторного произведения равняется площади параллелограмма, построенного на приведенных к общему началу векторова иb. Алгебраические свойства векторного произведения 1.  (антикоммутативность)2.  .3. [(  + ) ] = [  ] + [ ]; 4. для любого вектора " [ ] =  ;  12.Векторное произведение в декартовых координатах Теорема: Если векторы 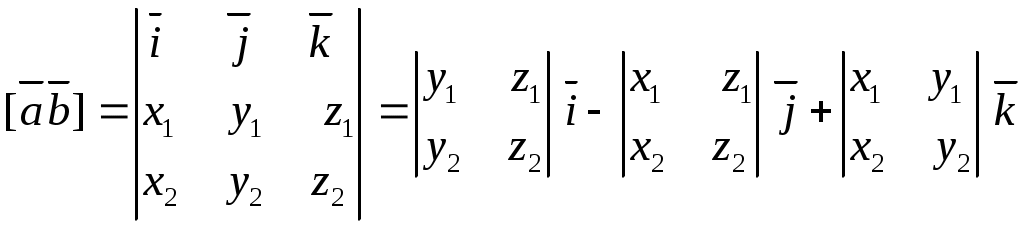 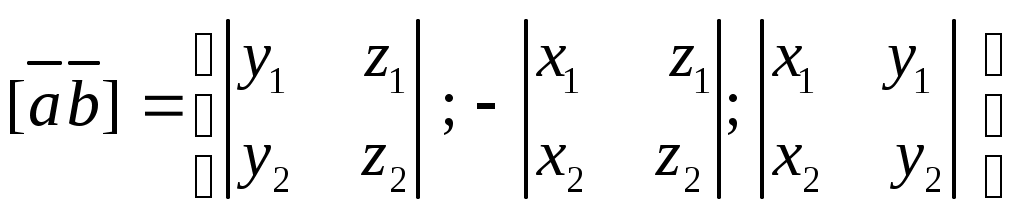иb определены своими декартовыми координатами  и  , то векторное произведение определяется .  .13. Смешанное произведение векторов. Геометрический смысл смешанного произведения. Определение:Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях. Определение:Пусть даны три произвольных вектораа,b ис. Если вектора векторно умножается на векторb, а затем получившийся при этом вектор скалярно умножается на векторс, то в результате получается число  , называемое смешанным произведением векторова,bис.Геометрический смысл смешанного произведения Теорема: Смешанное произведение равно объему параллелепипеда, построенного на приведенных общему началу вектораха,b ис, взятому со знаком плюс, если тройкааbс правая, и со знаком минус, если тройка аbс левая. Если векторыа,b ис компланарны, то равно 0.Следствие1: Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения. Следствие2: Смешанное произведение трех векторов, два из которых совпадают, равно нулю. Свойства смешанного произведения: 1. Смешанное произведение не зависит от группировки множителей:  .2. Смешанное произведение не изменяется от круговой перестановки множителей: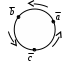  .3. Смешанное произведение суммы векторов на два других вектора равна сумме смешанных произведений каждого из векторов-слагаемых на два других вектора:  .4. Скалярный множитель можно выносить за знак смешанного произведения:  .14.Смешанное произведение в декартовых координтах Теорема: Если три вектора а,b ис определены своими декартовыми прямоугольными координатами 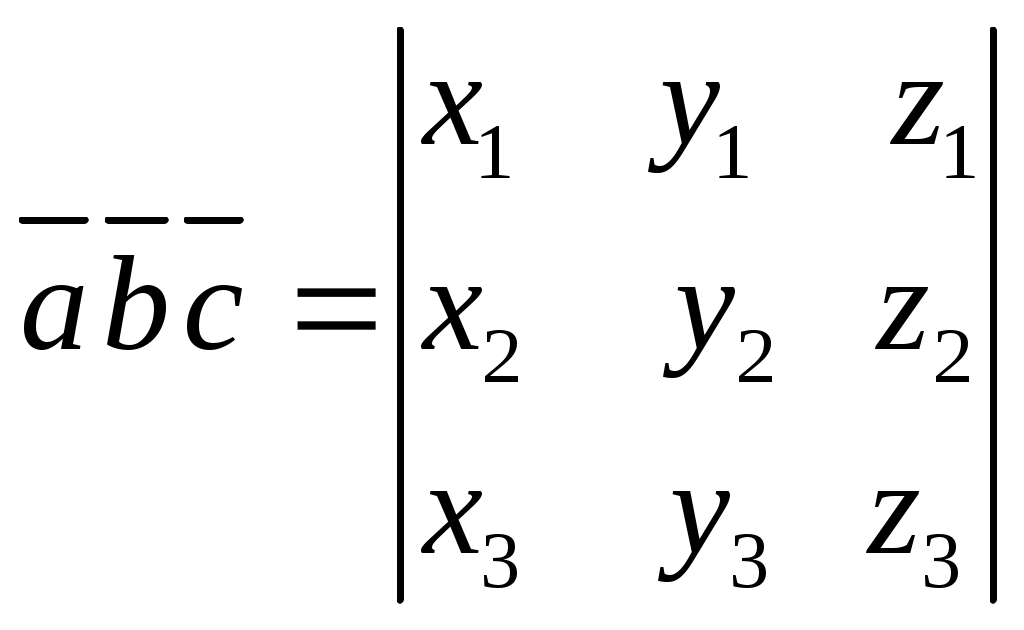 ,  ,  , то смешанное произведение  равняется определителю, строки которого равны координатам перемножаемых векторов. .Теорема: Для того чтобы три вектора были компланарными, необходимо и достаточно, чтобы их смешанное произведение было равно нулю. Следствие: Необходимым и достаточным условием компланарности трех векторов , , является равенство нулю определителя, строками которого служат координаты этих векторов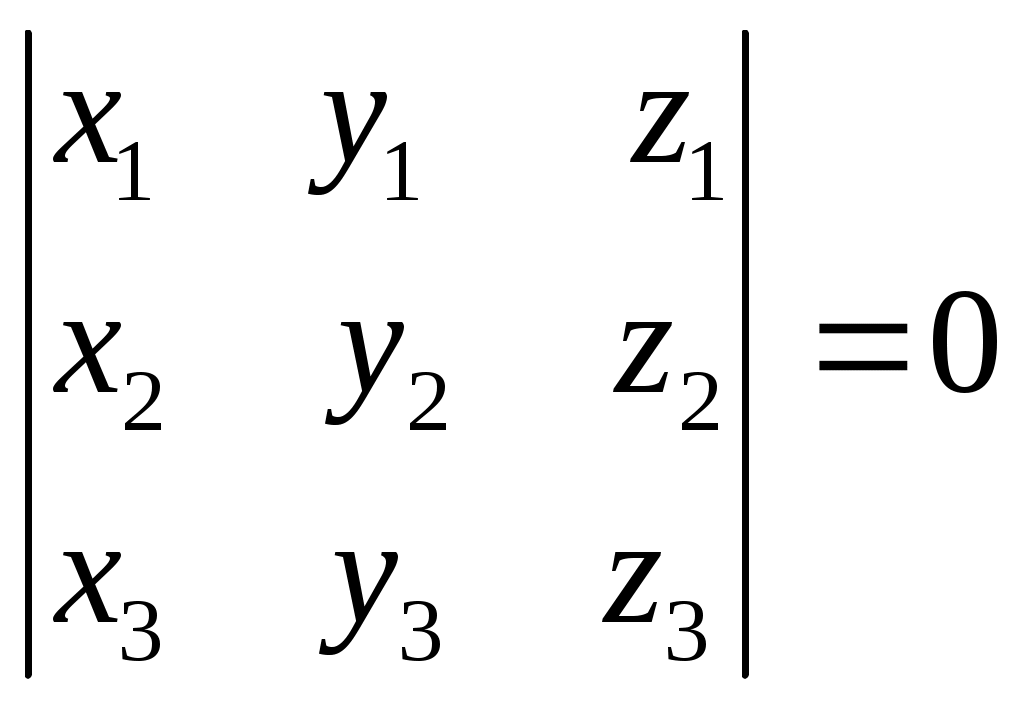. .15. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Неполные уравнения прямой. Уравнение прямой в отрезках. Общее уравнение прямой В декартовых координатах каждая прямая определяется уравнением первой степени, и обратно, каждое уравнение первой степени определяет прямую.  (1)Уравнение (1) с произвольными коэффициентами  , что А и В не равны нулю одновременно, называется общим уравнением прямой.Уравнение (1) имеет хотя бы одно решение  , то есть существует хотя бы одна точка  , координаты которой удовлетворяют уравнению (1)  (2) (Получили тождество). Из уравнения (1) вычитаем уравнение (2)  (3) Мы получили уравнение эквивалентное уравнению (1). Докажем, что уравнение (3) определяет прямую  , проходящую через точку , и перпендикулярно вектору  . Если точка  лежит на прямой , то её координаты удовлетворяют уравнению (3).Составим вектор  , . .Следовательно,  ортогональные векторы.Мы доказали, что прямая, определяемая общим уравнением (1), ортогональна к вектору . Вектор  называется нормальным вектором прямой (1) . Неполные уравнения прямой. Уравнение прямой в отрезках Общее уравнение (1) называется полным, если все его коэффициенты отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение называется неполным.Рассмотрим все возможные виды неполных уравнений. 1.  - прямая, проходящая через начало координат2.  - прямая, параллельная  ,   3.  или  - прямая, параллельная  ,  4.  определяет ось 5.  определяет ось  -(4) , уравнение (4) называется уравнением прямой «в отрезках».В уравнении (4) числа 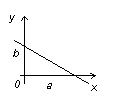 и  имеют простой геометрический смысл: они равны величинами отрезков, которые отсекает прямая на осях и соответственно:  16. Уравнение прямой проходящей через данную точку и имеющий угловой коэффициент. Уравнение прямой проходящей через две данные точки. Прямая с угловым коэффициентом Рассмотрим произвольную прямую, не параллельную оси 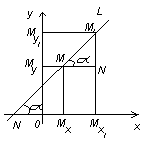. Введем понятие угла наклона прямой к оси . - угол, на который надо повернуть против часовой стрелки ось до совпадения с прямой .Тангенс угла наклона прямой к оси называется угловым коэффициентом прямой и обозначается    (5)-уравнение прямой, проходящей через точку , и имеющей угловой коэффициент  . . Примем выражение  за , тогда получим  (6)Уравнение (6) называется уравнением прямой с угловым коэффициентом. - величина отрезка, отсекаемого данной прямой на оси , начиная от начала координат.Если прямая задана общим уравнением  , то её угловой коэффициент  .Уравнение прямой проходящей через две данные точки 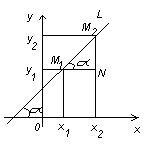 Рассмотрим треугольник.  = , |