билеты геометрия. Билеты аналитическая геометрия. 1. Декартовы координаты на прямой
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
Исследование формы эллипса1. Симметрия. Так как каноническое уравнение эллипса содержит только квадраты текущих координат, то если точка (х, у) находится на эллипсе, то и точка Ось симметрии эллипса, на которой располагаются фокусы, называется фокальной осью. Точка пересечения осей симметрии эллипса – центр эллипса. 2. Точки пересечения эллипса с осями симметрии называются его вершинами. А1(а; 0), А2(-а; 0), В1(0; b), B2(0; -b) – вершины эллипса. Отрезки А1А2 и В1В2, соединяющие противоположные вершины эллипса, а также их длина 2а и 2b называют соответственно большой и малой осями эллипса. а – большая полуось, b – малая полуось. 3. Форма эллипса. Чтобы исследовать форму эллипса, в уравнении Из (1) 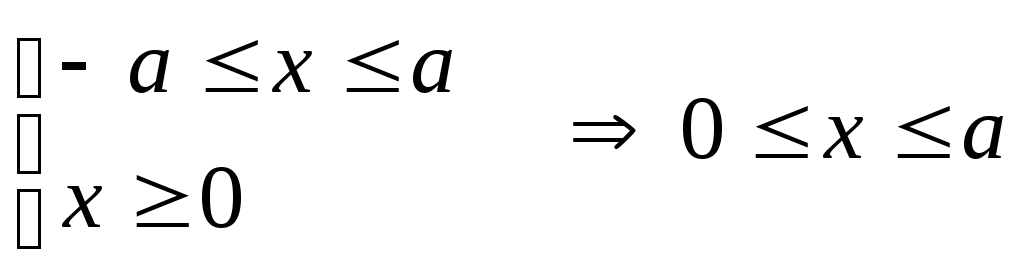 . .С увеличением х от 0 до а, у уменьшается от b до 0. 4. Эксцентриситет и директрисы эллипса. Величина Так как, 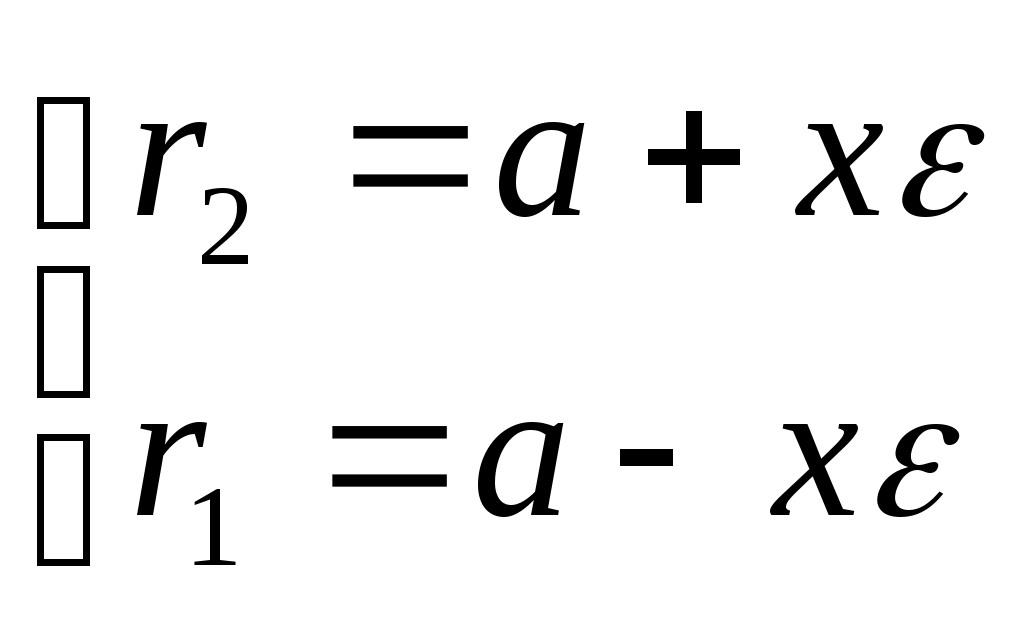 выражение формулы для фокальных радиусов эллипса. выражение формулы для фокальных радиусов эллипса.Опрделение: Две прямые перпендикулярные к фокальной оси эллипса и отстоящие (от нее) на расстояние Свойство директрисы : Отношение расстояний от любой точки эллипса до фокуса соответствующей директрисы есть величина постоянная равная . 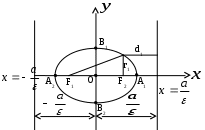 - свойство директрисы. - свойство директрисы.28. Каноническое уравнение гиперболы. Директриса и эксцентриситет гиперболы. Определение: Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек, называемых фокусами, есть постоянная величина равная 2а. Указанная разность берется по абсолютному значению и обозначается через 2а. Фокусы гиперболы обозначают буквами F1F2 = 2c. По определению 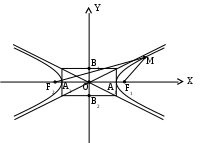 Пусть дана гипербола. Выберем оси координат так же, как и в эллипсе. То в этой системе координат уравнение гиперболы имеет вид: Исследование гиперболы 1. Из канонического уравнения видно, что гипербола имеет две оси симметрии, так как х и у входят во вторую степень. Одна ось проходит через фокусы и называется действительной осью гиперболы. Вторая ось перпендикулярна первой, проходит через начало координат и называется мнимой осью гиперболы. 2. Пересечение гиперболы с осью А1(а, 0), А2(- а, 0) Пересечение гиперболы с осью Действительная ось гиперболы пересекает гиперболу в двух точках А1 и А2, которые называются вершинами гиперболы. 2а – большая ось, а – большая полуось 2b – малая ось, b – малая полуось 3. Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы. Диагонали основания прямоугольника являются асимптотами гиперболы. В1(0, b), B2(0, - b) 4. Величина > 1 Эксцентриситет гиперболы характеризует форму ее основного прямоугольника, значит и форму самой гиперболы. Чем меньше , тем больше вытянут ее основания прямоугольник. 5. Гипербола, полуоси которой равны, называется равносторонней. a  = b = b 6. Гипербола 7. Выражения фокальных радиусов гиперболы. 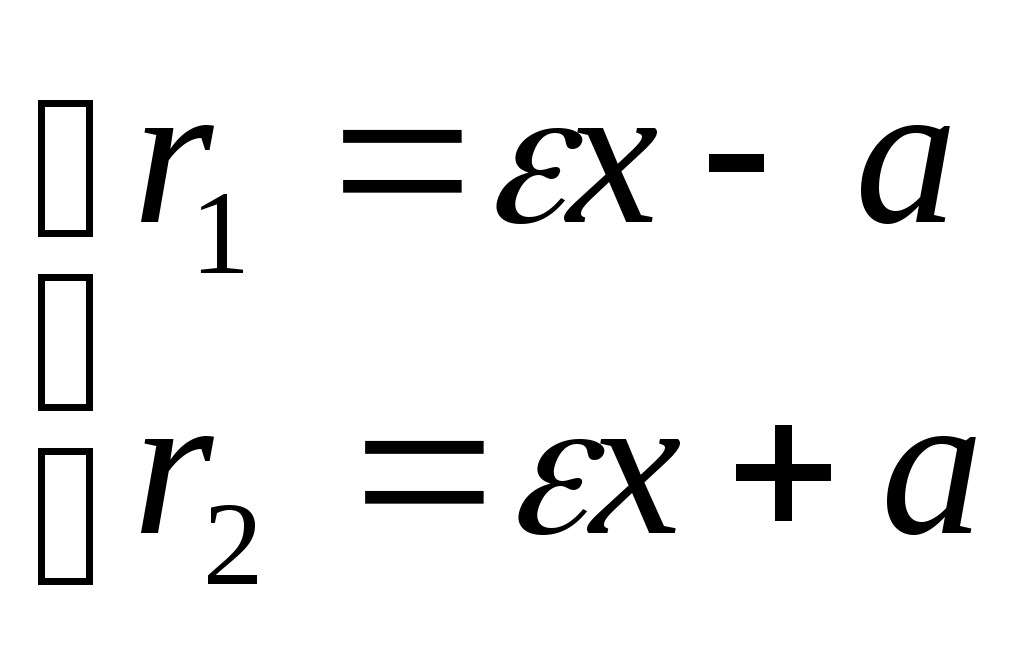 - для правой ветви гиперболы - для правой ветви гиперболы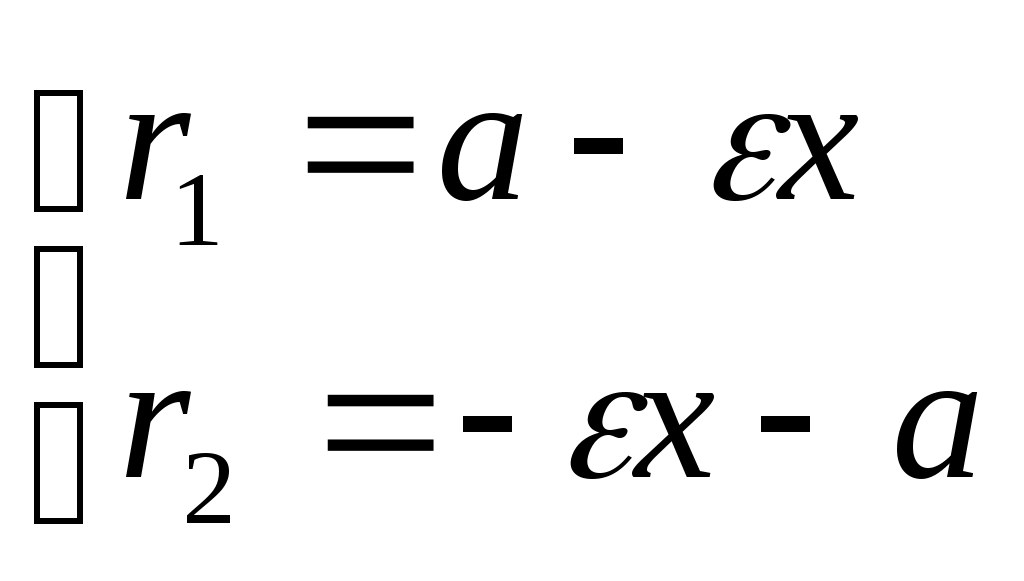 - для левой ветви гиперболы - для левой ветви гиперболы 8. Директрисы гиперболы. Определение: Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположена относительно центра на расстоянии 9. Свойство директрисы: Если r– расстояние от произвольной точки гиперболы до какого-нибудь фокуса, а d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение 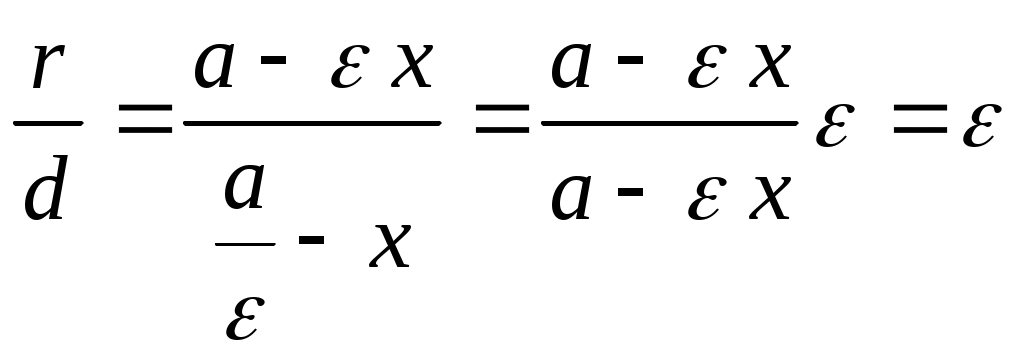 29. Каноническое уравнение параболы. Директриса параболы Уравнение параболы, свойства Определение: Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокусы параболы обозначается буквой F, расстояние от фокуса до директрисы – буквой p . Число p называется параметром параболы. Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посредине между фокусом и директрисой. В этой системе координат данная парабола будет определяться уравнением: В этой же системе координат директриса данной параболы имеет уравнение: 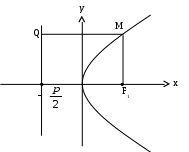 |
