билеты геометрия. Билеты аналитическая геометрия. 1. Декартовы координаты на прямой
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
32.Параболоиды Поверхность, определяемая уравнением (4), называется эллиптическим параболоидом. 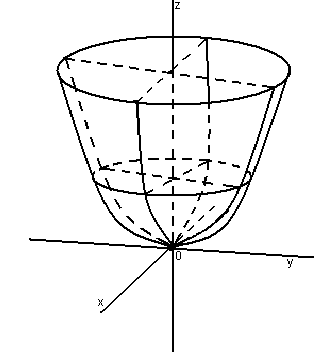 Исследуем эту поверхность методом сечений. Так как в уравнение поверхности переменные X и Y входят только во второй степени, а Z –только в первой, то это значит, что эллиптический параболоид, определяемый уравнением (4), симметричен относительно плоскостей XOZ и YOZ. Ось OZ является осью симметрии эллиптического параболоида, она пересекает поверхность только в начале координат. Начало координат называется вершиной эллиптического параболоида. Плоскость X=0 пересекает эллиптический параболоид по параболе 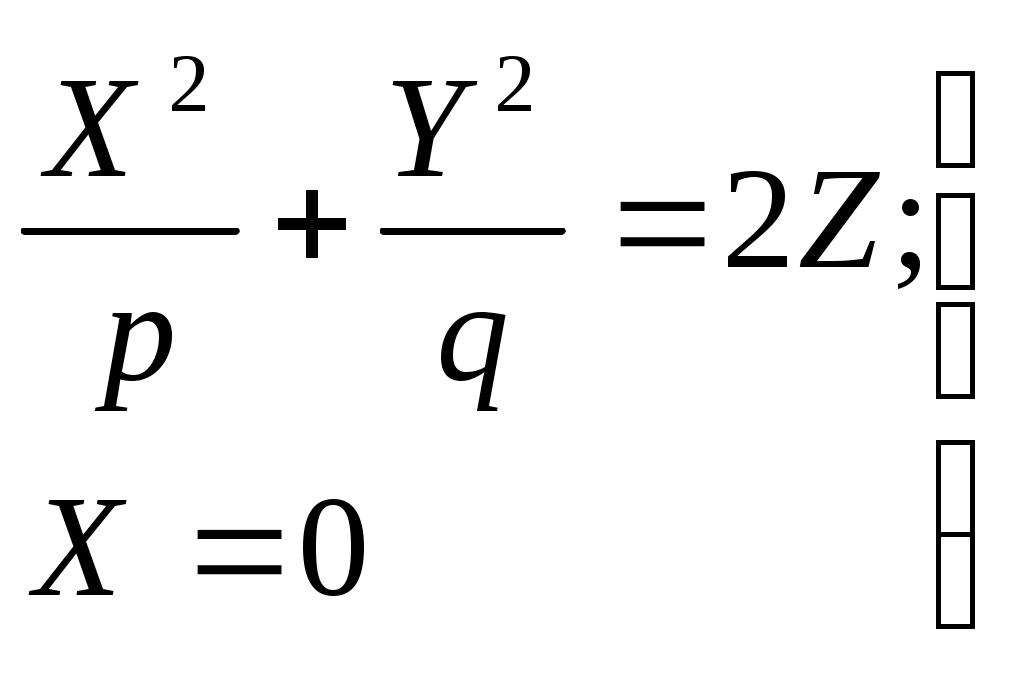 или или 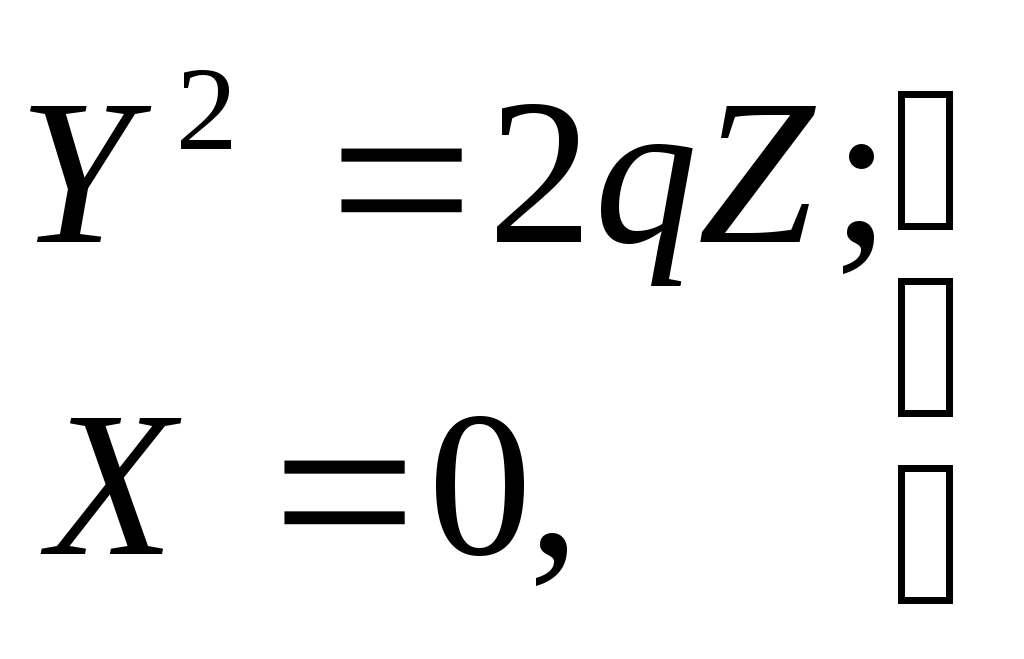 плоскость Y=0 –по параболе 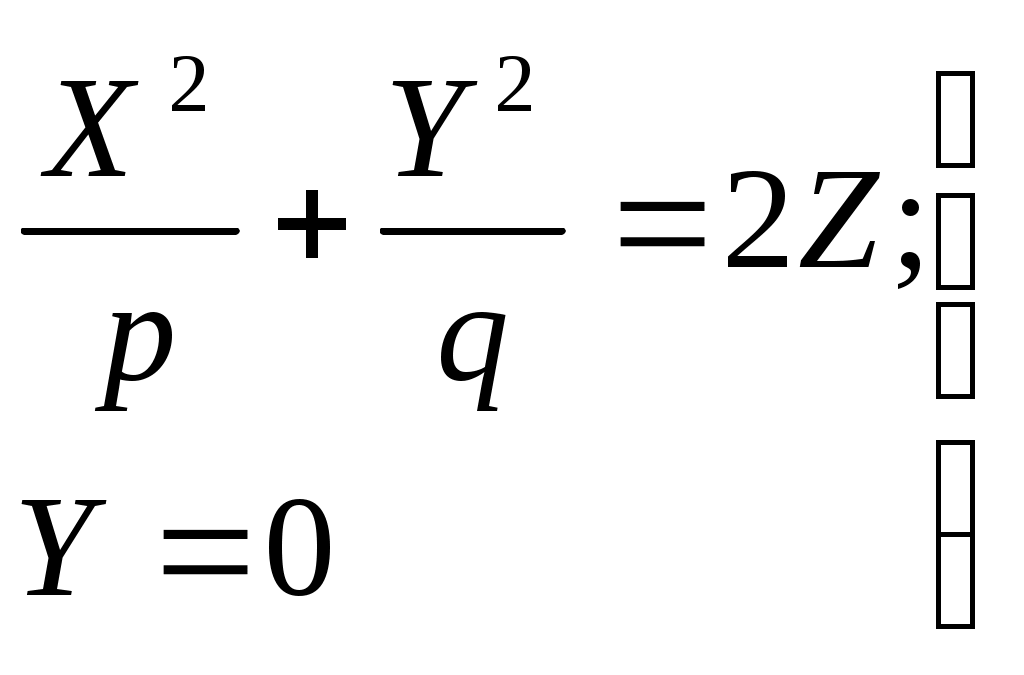 или или 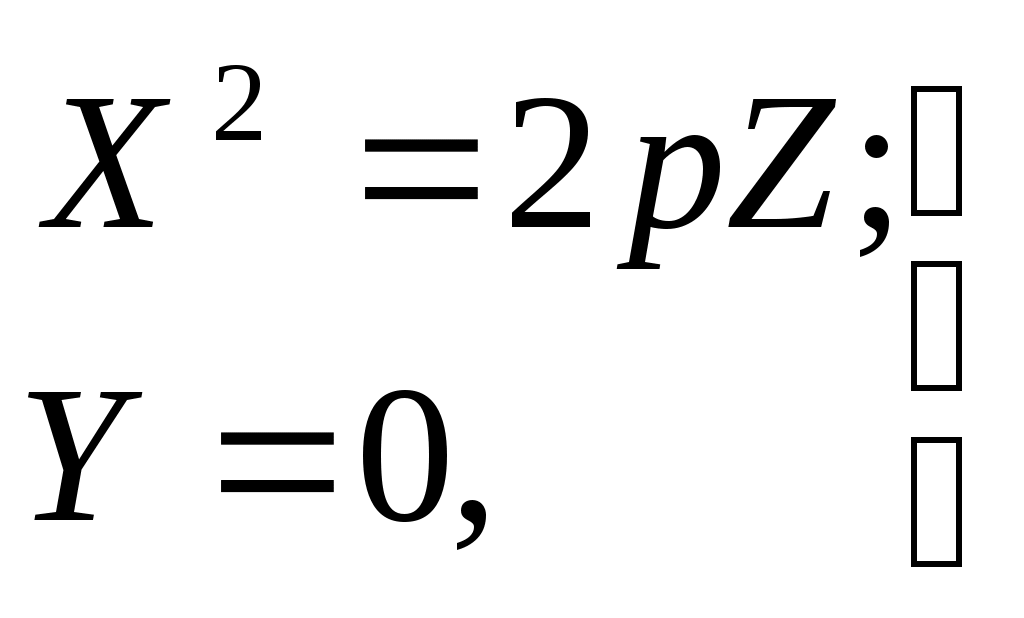 Следовательно, p и q –параметры парабол, получающихся при пересечении эллиптического параболоида его плоскостями симметрии. Плоскость Z=h пересекает эллиптический параболоид по линии 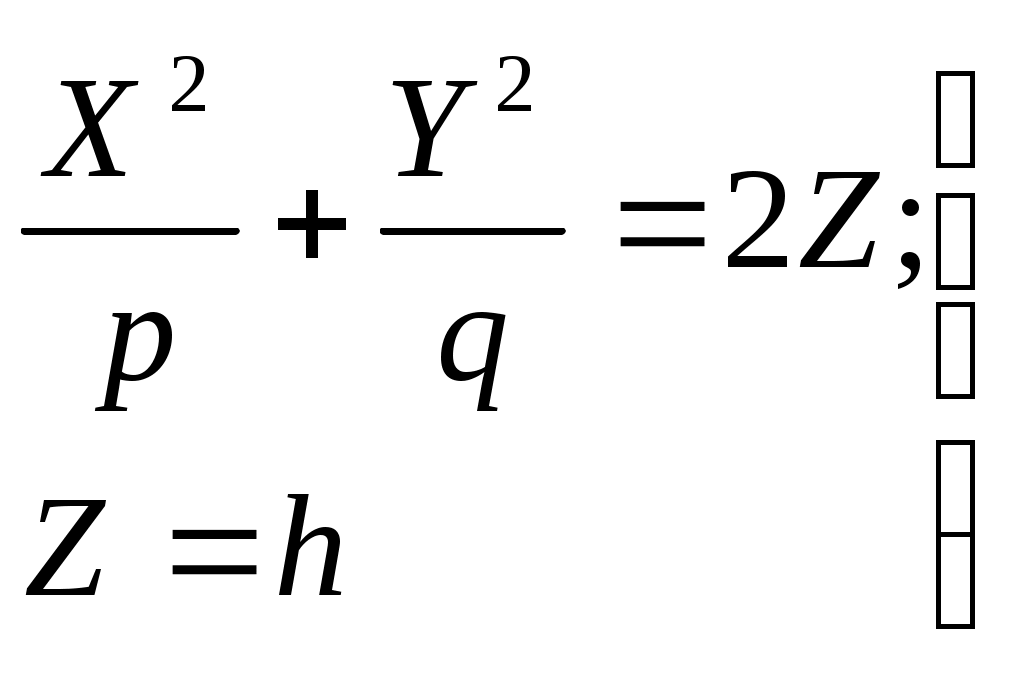 или или 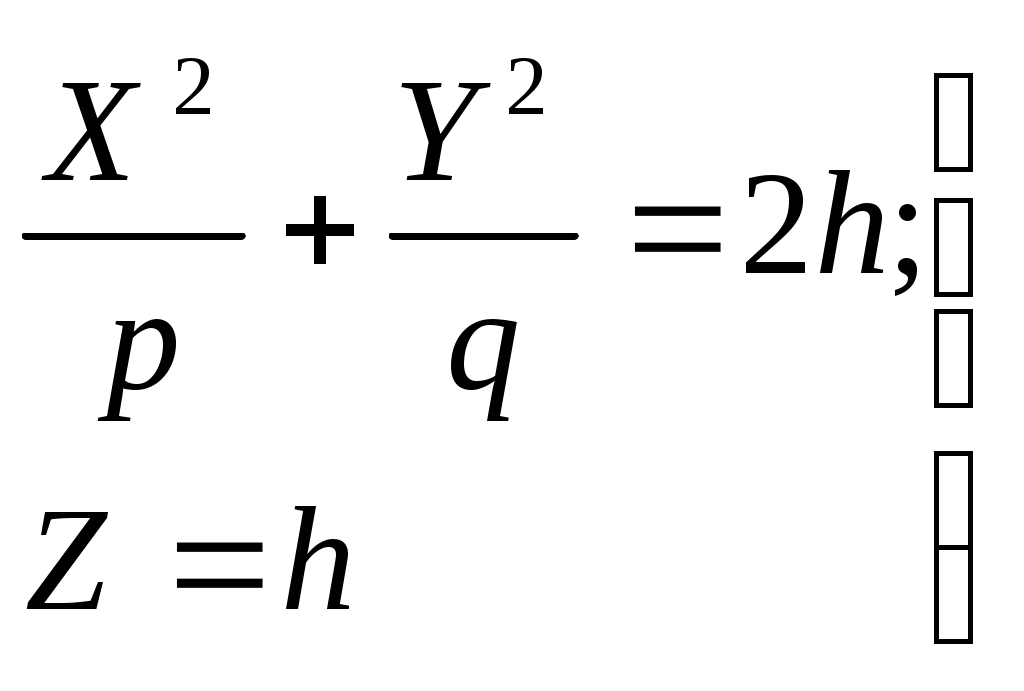 Если h>0, то в сечении образуется эллипс 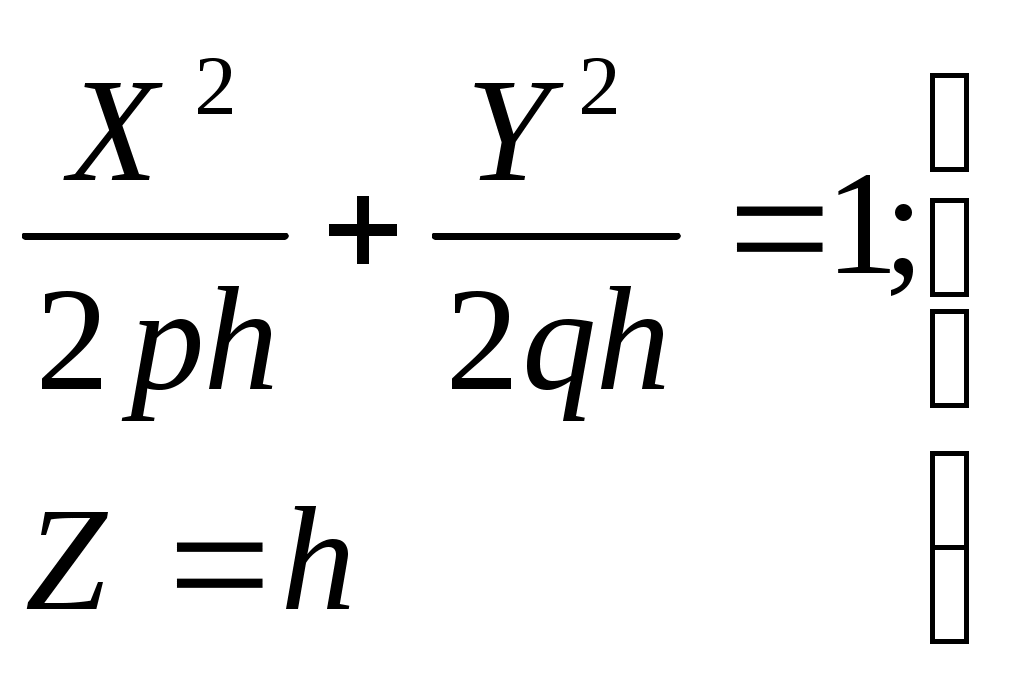 При h=0 в сечении получается точка. Значит, поверхность имеет с плоскостью XOY одну точку – начало координат. Если h<0, то сечением является мнимый эллипс, так как по условию p>0 и q>0. Следовательно, поверхность расположена по одну сторону от плоскости XOY. Гиперболический параболоид. Поверхность, определяемая относительно некоторой прямоугольной декартовой системы координат уравнением где p>0; q>0, называется гиперболическим параболоидом. Исследуем эту поверхность методом сечений. 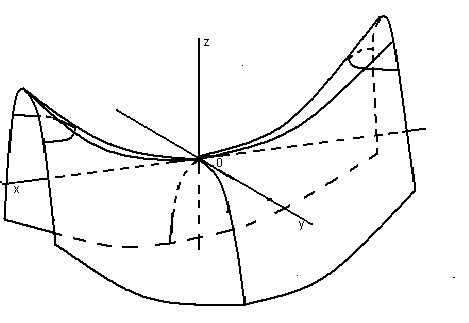 Так как в уравнение (5) поверхности переменные x и y входят только во второй степени, а переменная z – в первой, то это значит, что поверхность симметрична относительно плоскостей xOz и yOz. Ось Ozявляется осью симметрии гиперболического параболоида, она пересекает гиперболический параболоид, определяемый уравнением (5), в начале координат – его вершине. Плоскость y=0 пересекает гиперболический параболоид по параболе 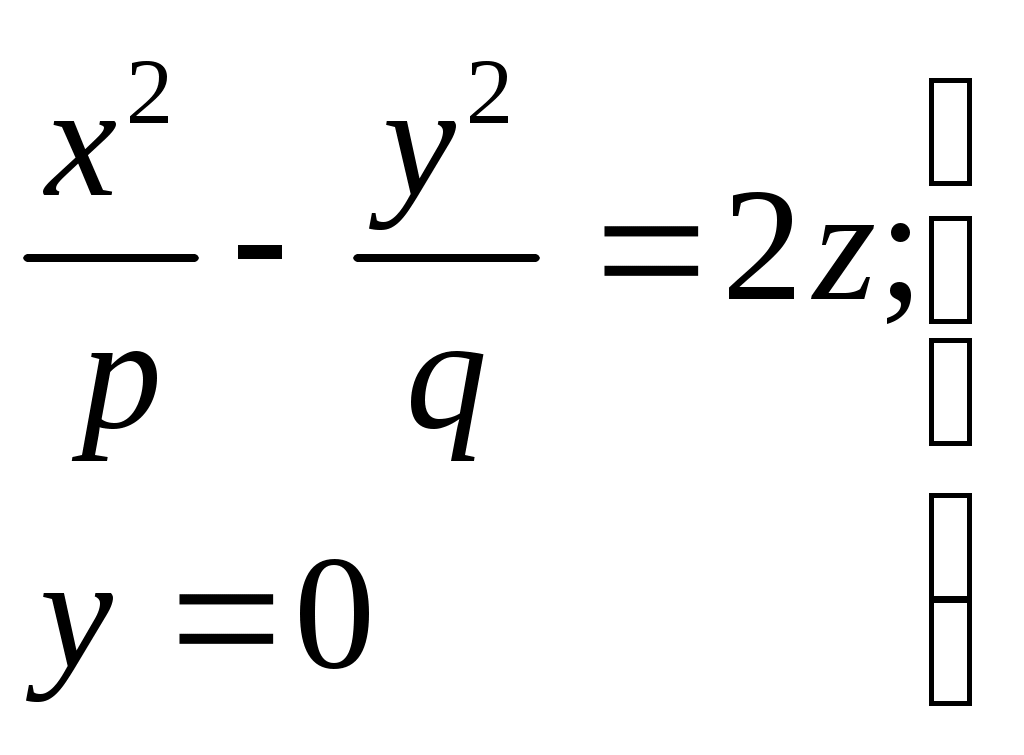 или или 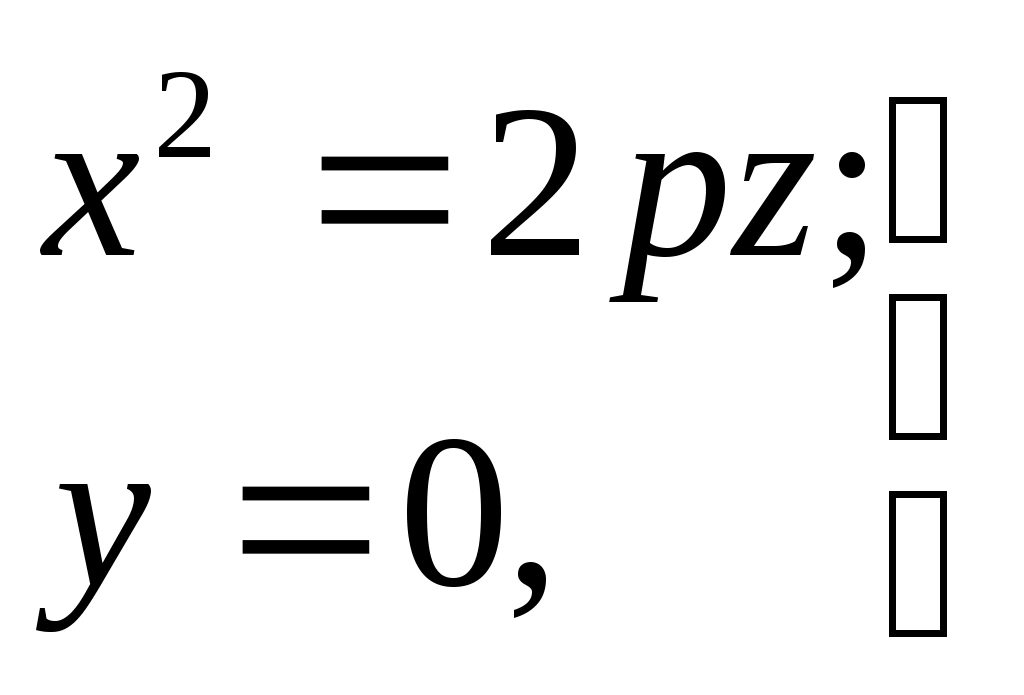 плоскость x=0 – по параболе 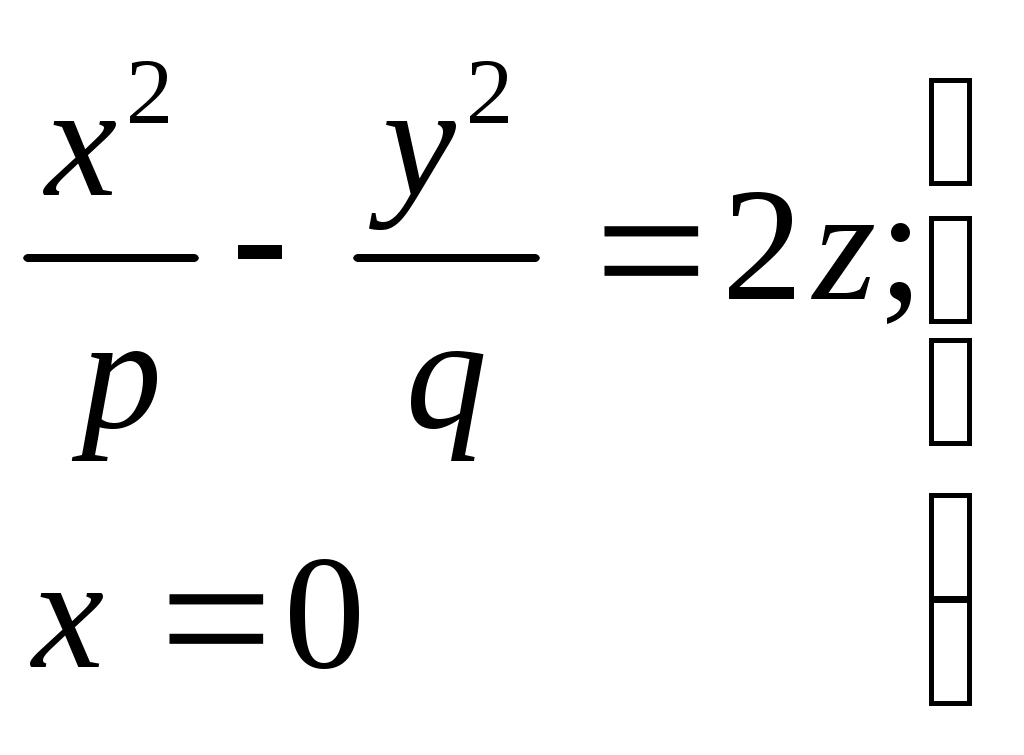 или или 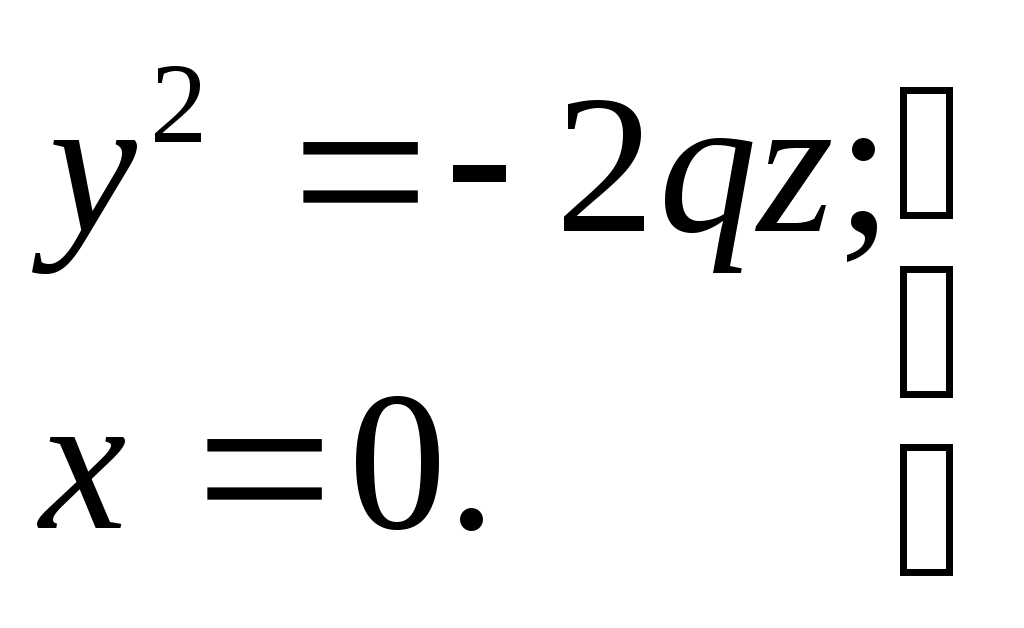 Следовательно, pи q – параметры парабол, получающихся при пересечении гиперболического параболоид его плоскостями симметрии. В сечении гиперболического параболоида плоскостью z=h получим линию 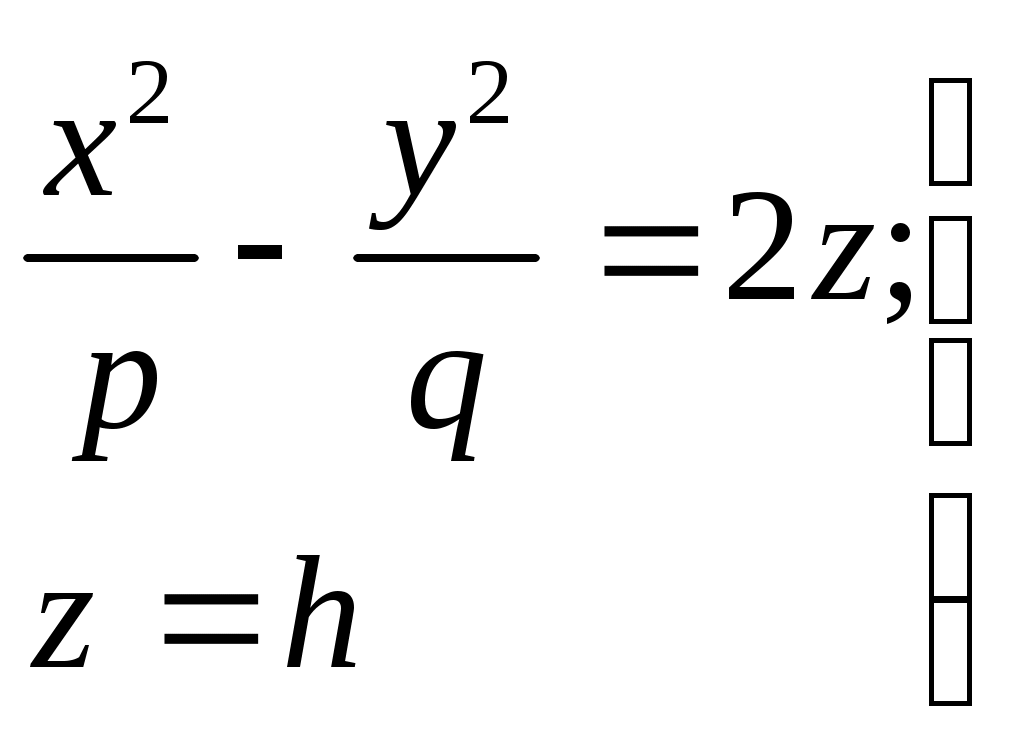 или или 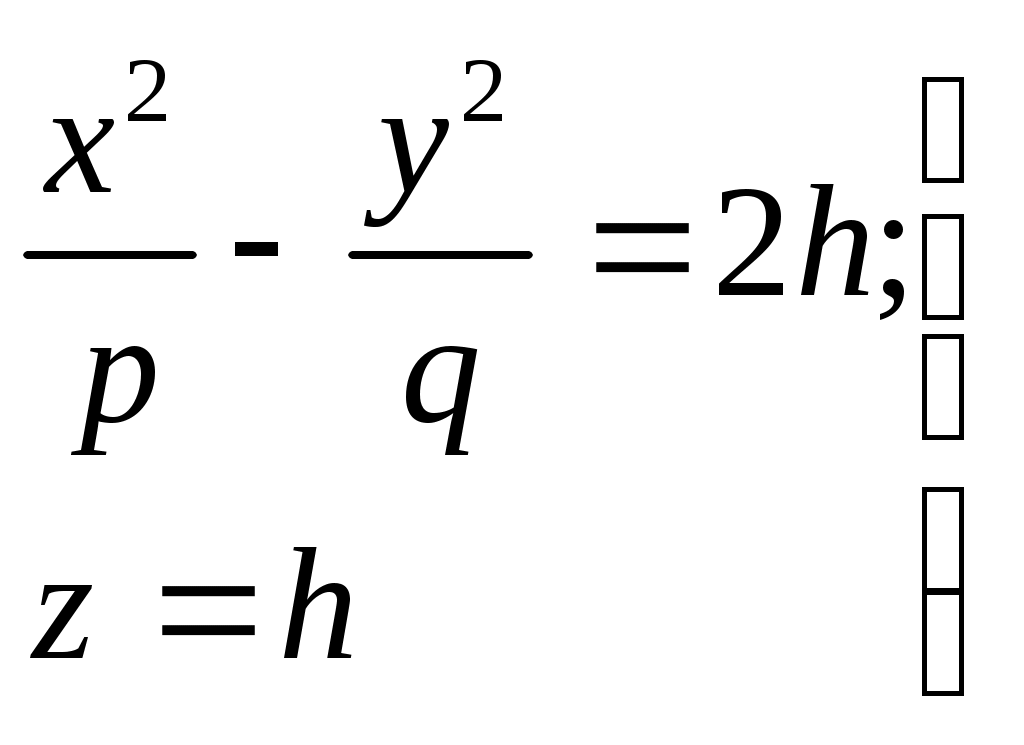 Если h>0, то сечением является гипербола, действительная ось которой параллельна оси Ox; центр гиперболы находится в точке (0, 0, h). При h=0 в сечении получаются две прямые: 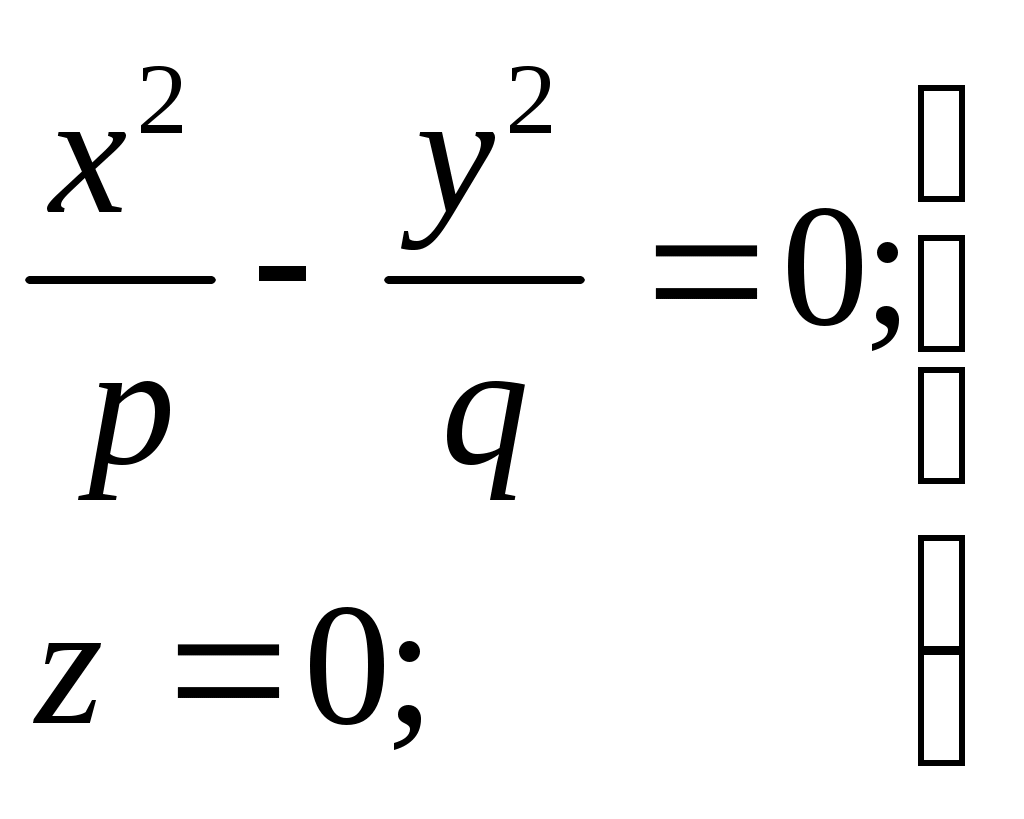 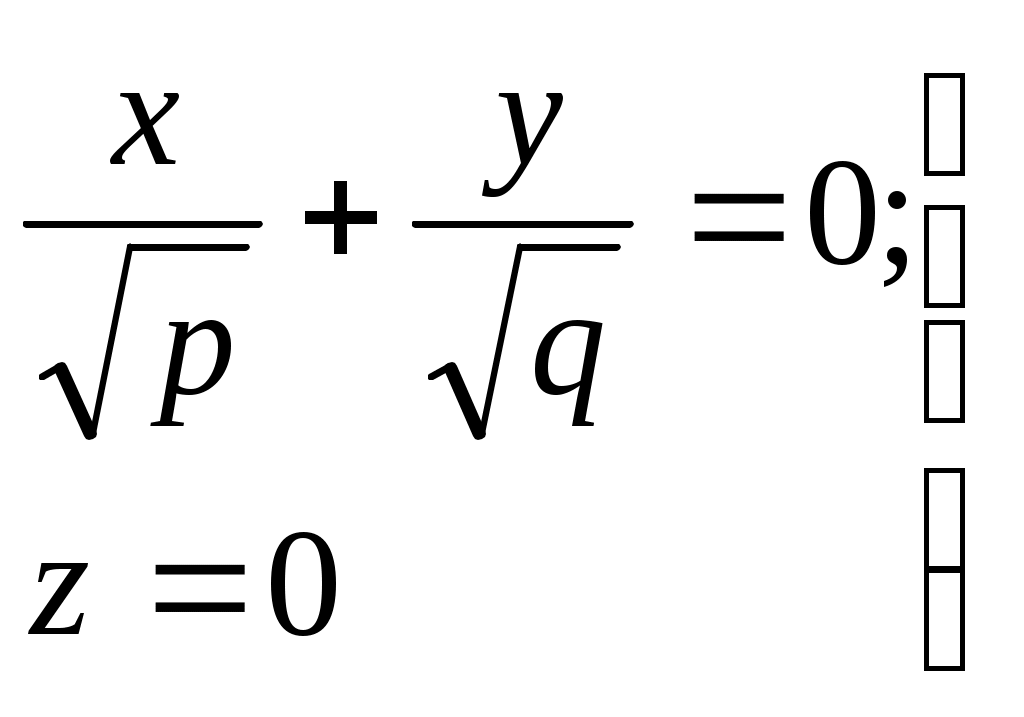 или 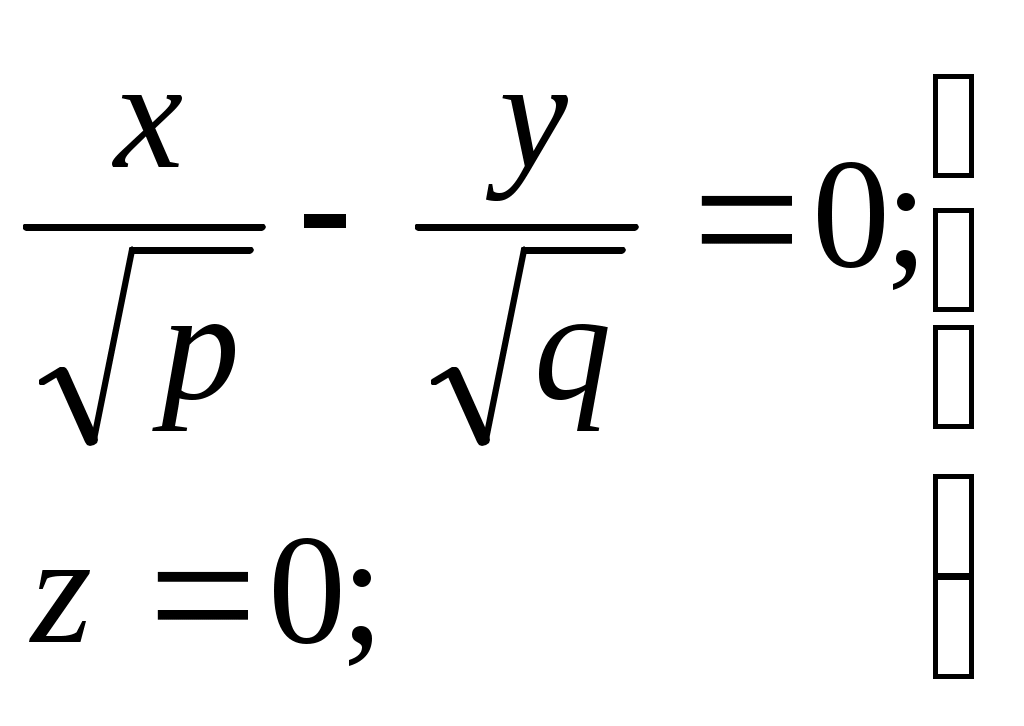 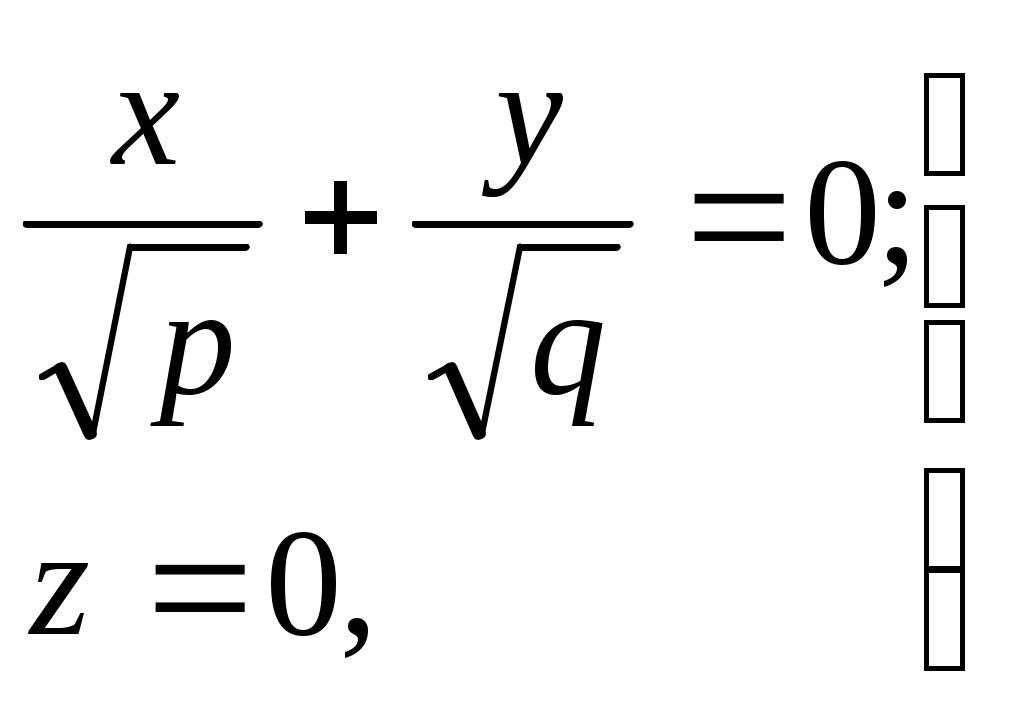 которые называются прямолинейными образующими гиперболического параболоида. Если h<0, то сечением является гипербола, ось которой параллельна оси Oy. Найдем сечения гиперболического параболоида плоскостями, параллельными плоскости yOz. В сечении плоскостью x=h получаем параболу 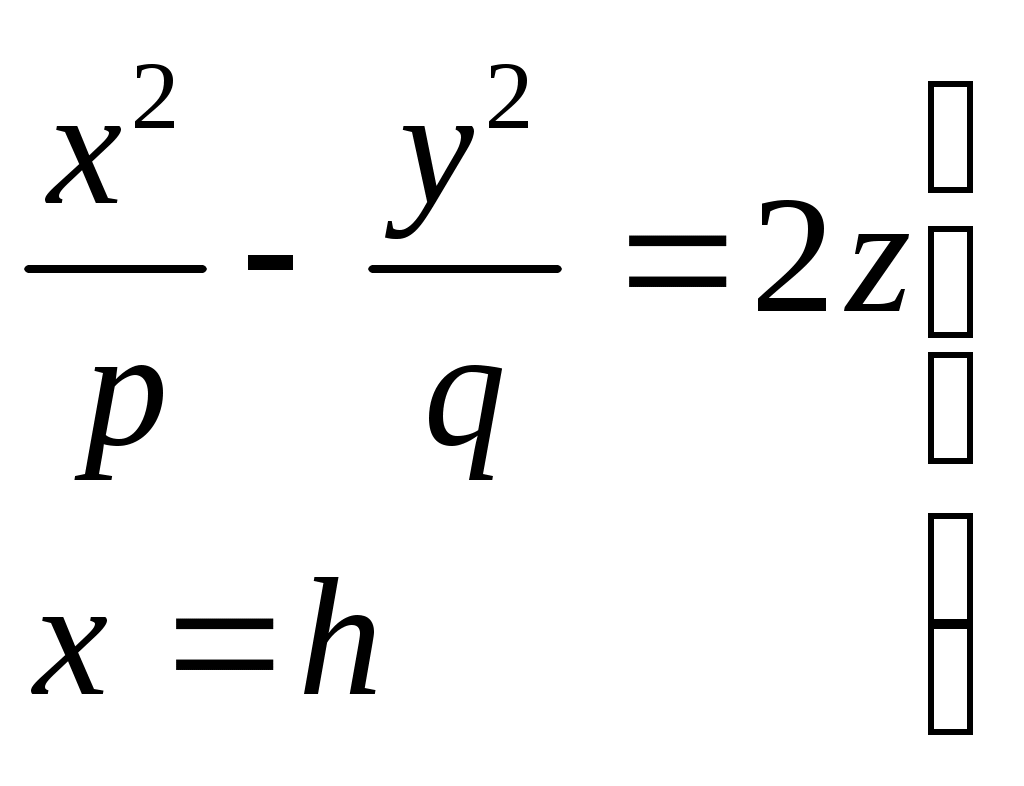 или или 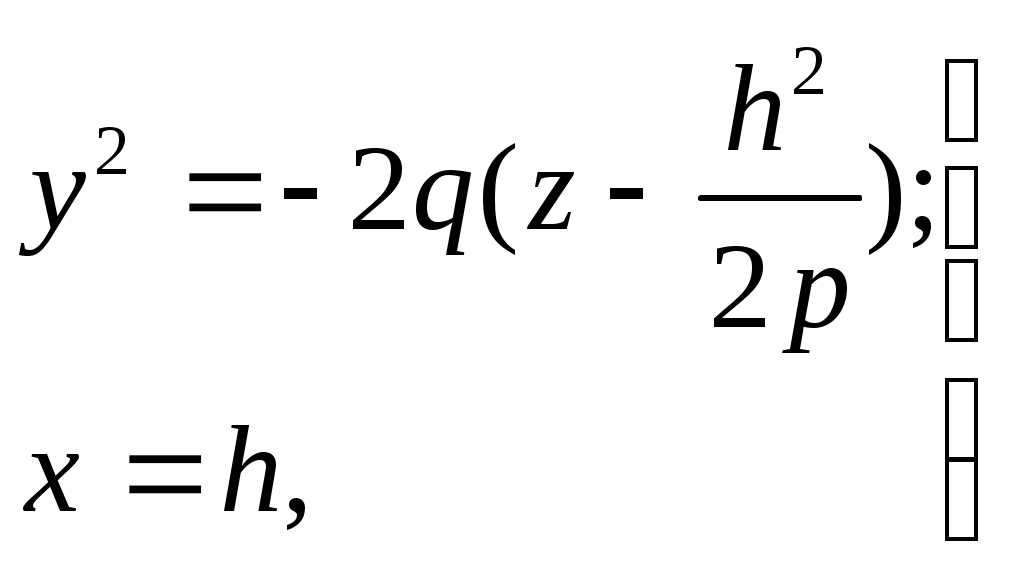 ось симметрии которой параллельна оси Oz и вершина находится в точке (h; 0; гиперболический параболоид может быть получен при параллельном переносе параболы, лежащей в плоскости yOz, при условии, что ее вершина скользит по параболе, лежащей в плоскости xOz. 33. Конус второго порядка и цилиндр. Поверхность определяемая уравнением 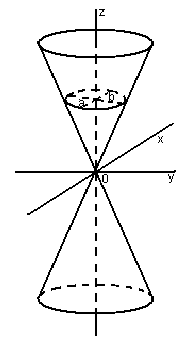 Так как в уравнение поверхности переменные X,Y,Z входят только во второй степени, это значит, что поверхность симметрична относительно всех трех координатных плоскостей и координатных осей. Начало координат является центром симметрии поверхности. Оно называется вершиной конуса второго порядка. Найдем сечения поверхности ее плоскостями симметрии. Сечениями конуса второго порядка плоскостями yOz и xOz является пара пересекающихся прямых: 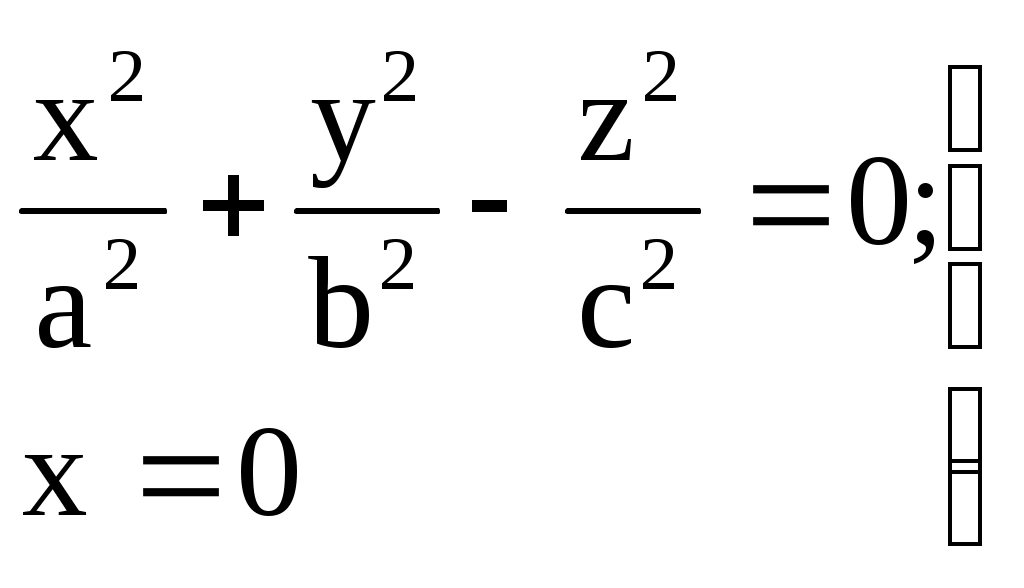 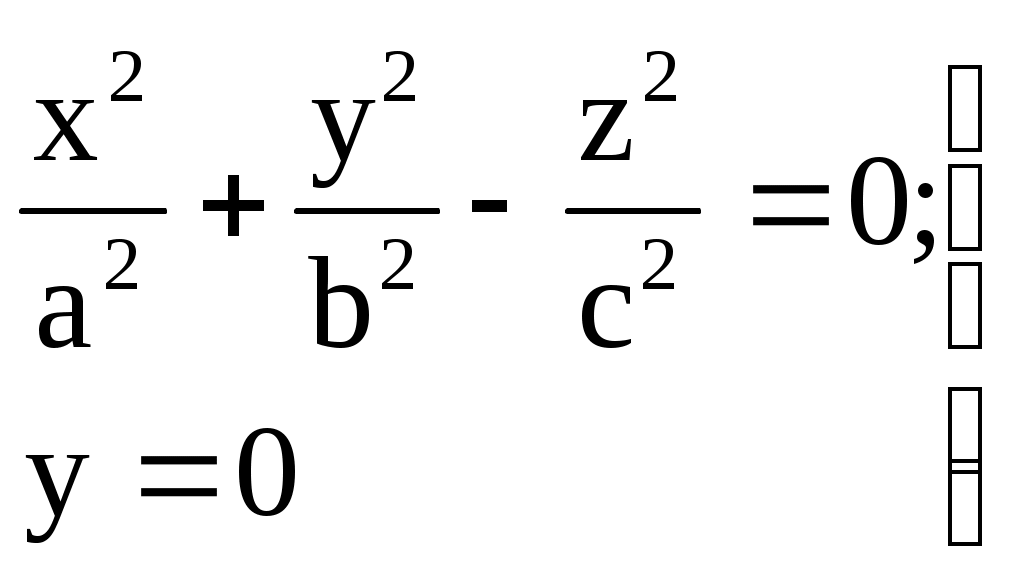 или или 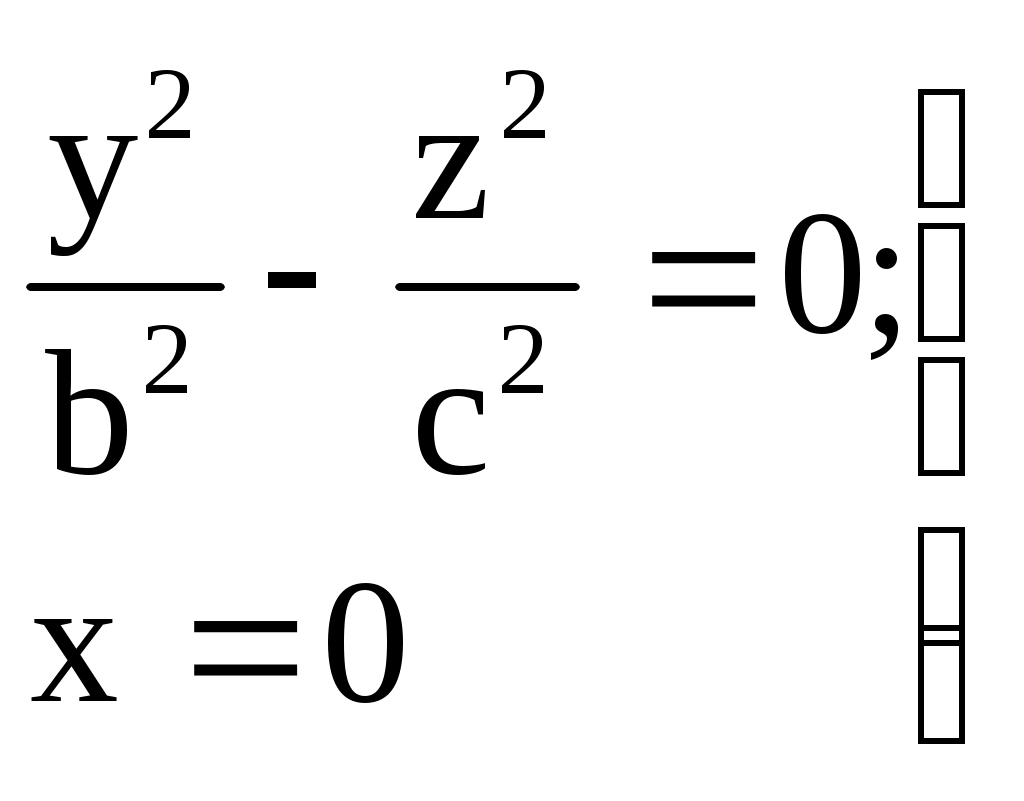 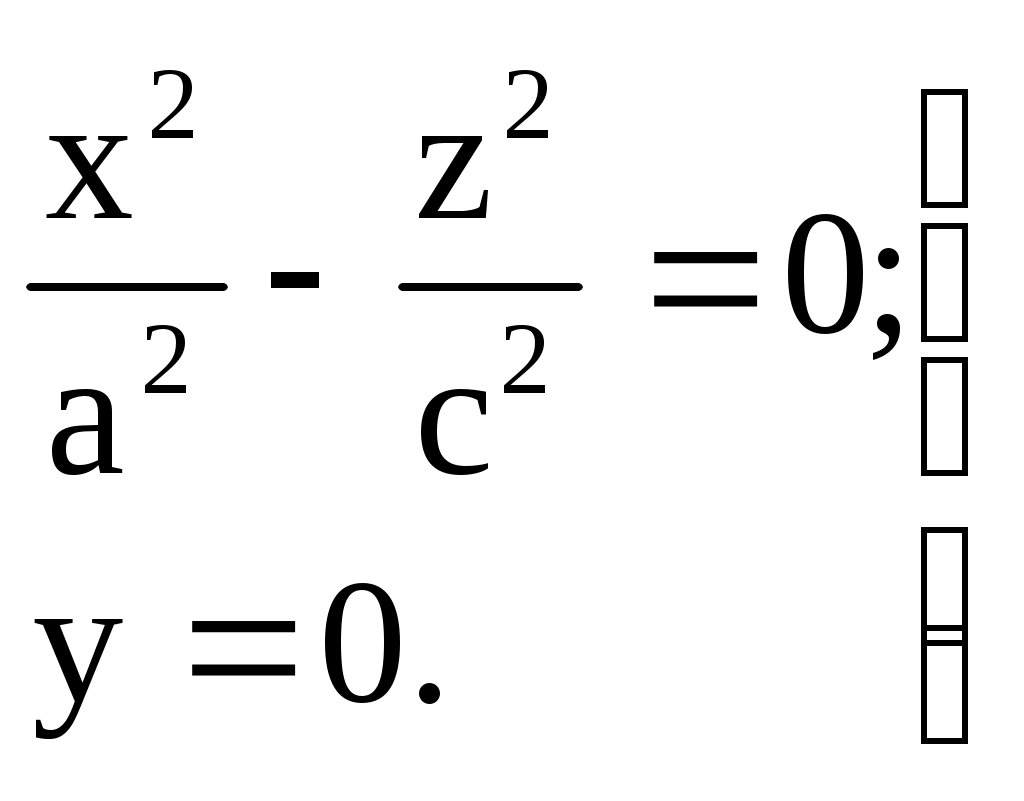 Поскольку xOy имеет с конусом второго порядка, определяемым уравнением (6), только одну общую точку – начало координат (вершину конической поверхности). Плоскость z=h пересекает конус второго порядка по эллипсу 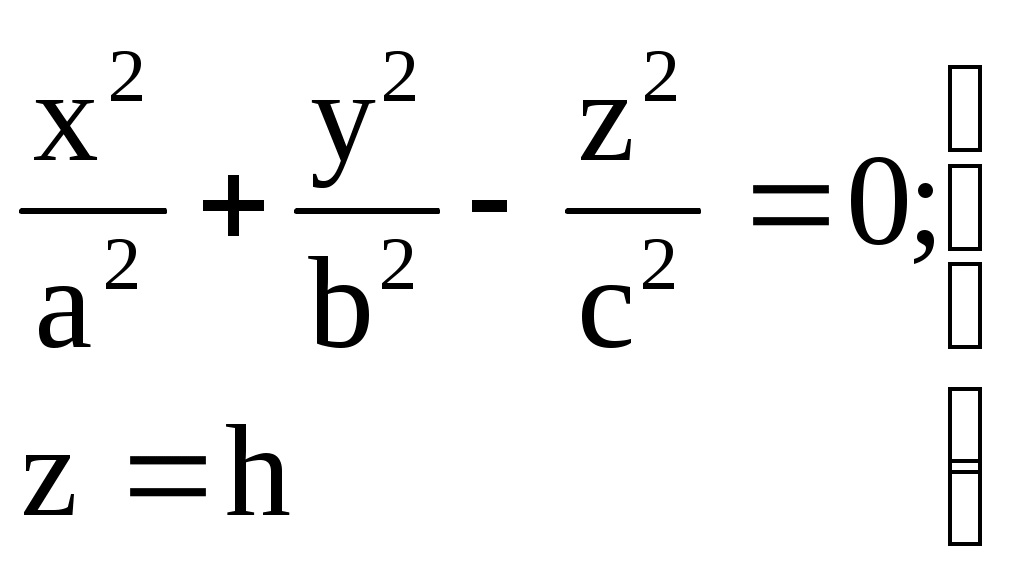 или или 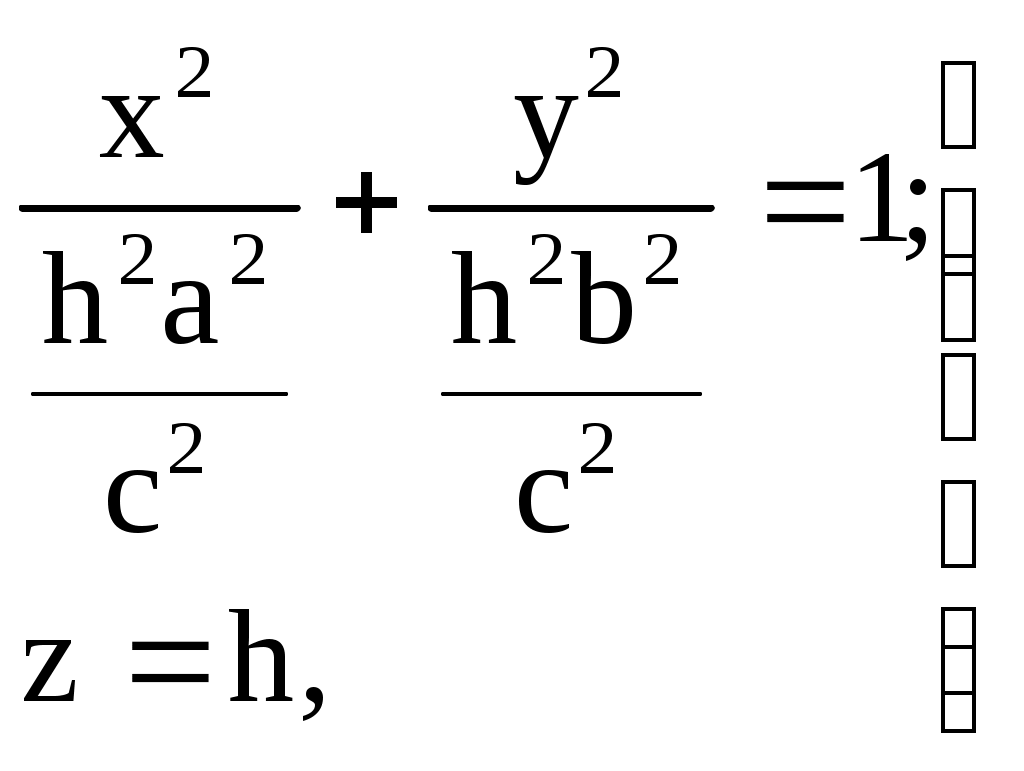 Полуоси которого увеличиваются с возрастанием Цилиндрические поверхности Цилиндрическая поверхность – это поверхность, образованная при поступательном движении прямой, называемой образующей, проходящей через все точки некоторой линии, называемой направляющей. Существует три типа цилиндров второго порядка: 1) эллиптический цилиндр 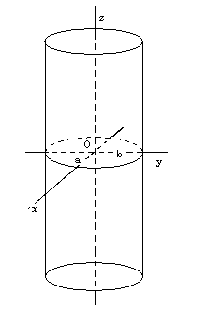 2) гиперболический цилиндр 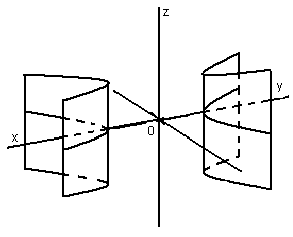 3) параболический цилиндр 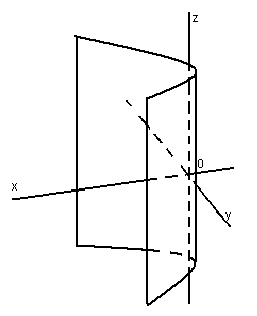 |
