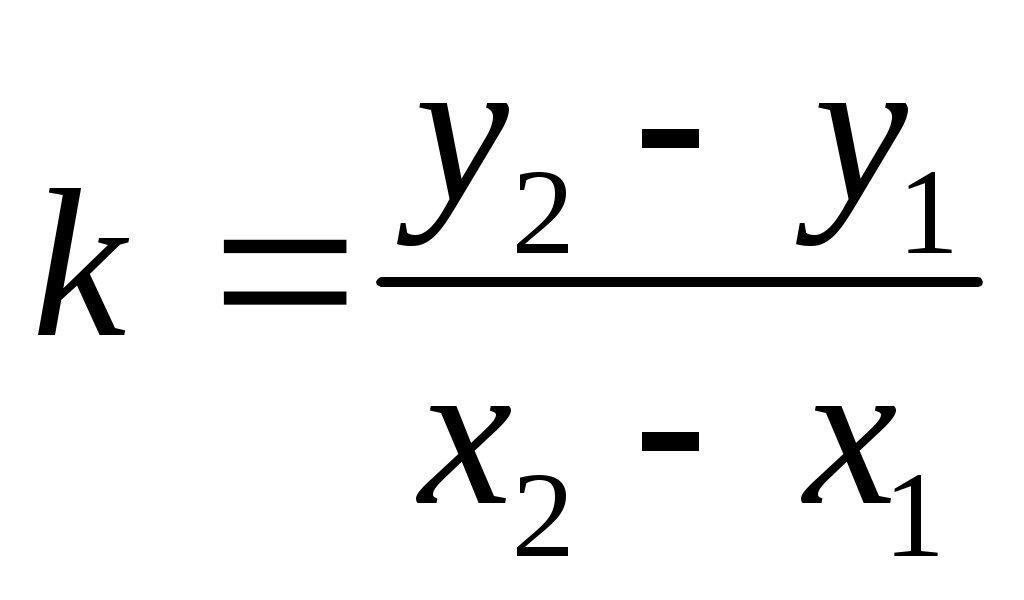 , ,
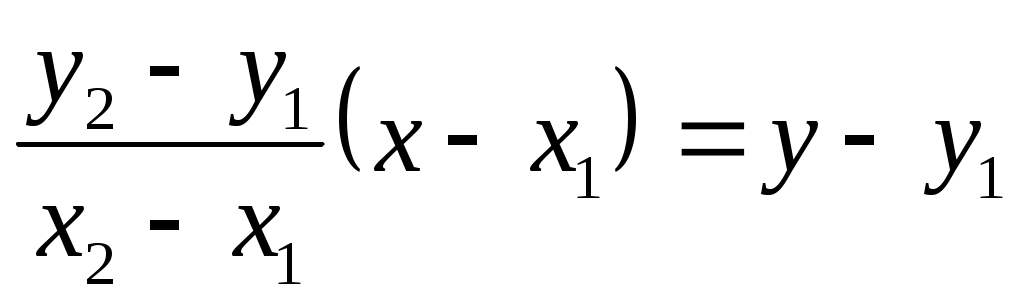 , преобразовывая, получим , преобразовывая, получим 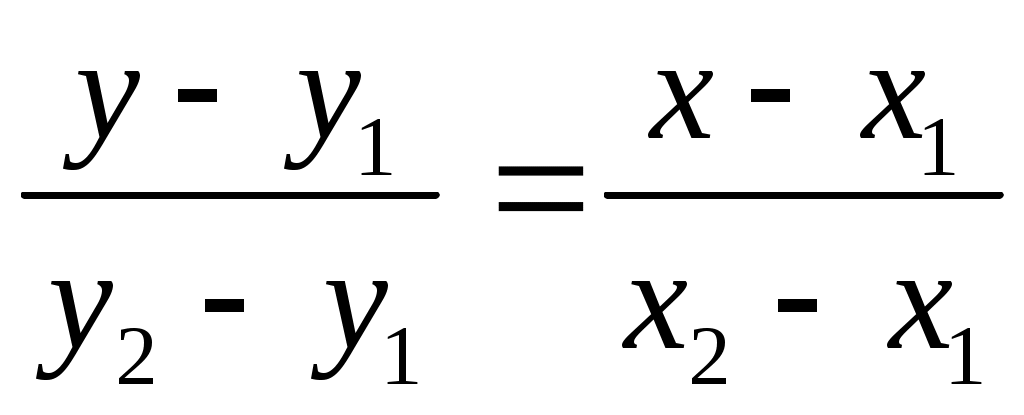 (7), уравнение (7) является уравнением прямой, проходящей через две данные точки. (7), уравнение (7) является уравнением прямой, проходящей через две данные точки.
17. Угол между двумя прямыми на плоскости, условия параллельности и перпендикулярности двух прямых.
Угол между двумя прямыми. Условие перпендикулярности и параллельности двух прямых
а) Пусть даны две прямые 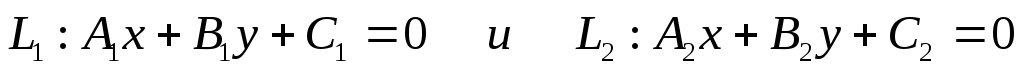
Нормальным вектором прямой 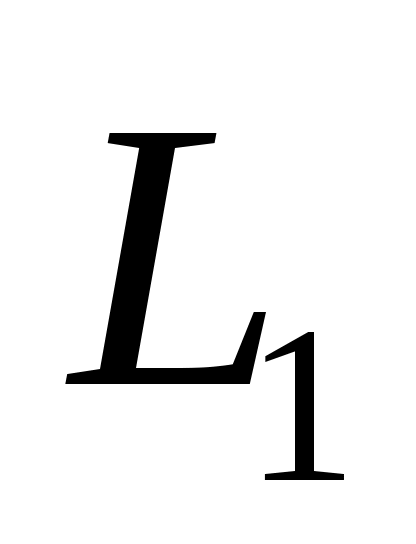 является вектор является вектор 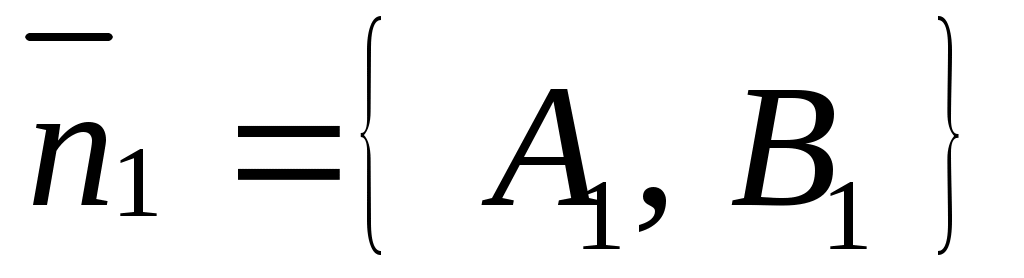 , а нормальным вектором прямой , а нормальным вектором прямой 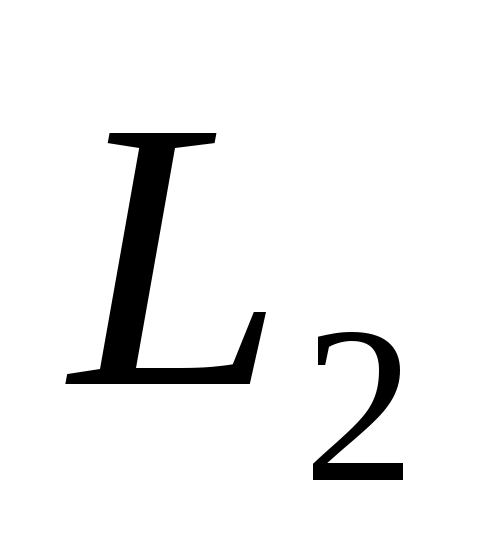 является вектор является вектор 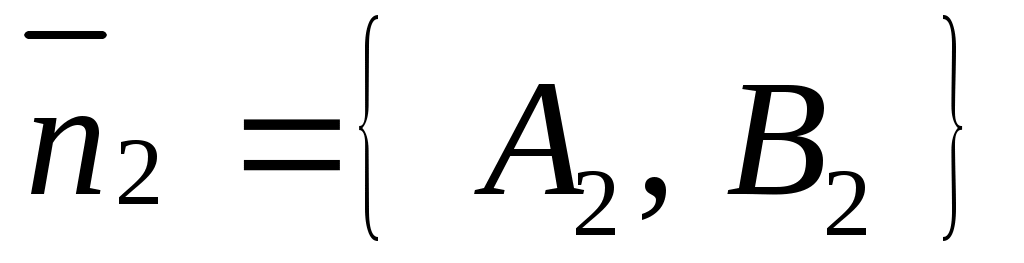 . Задача об определении угла между этими двумя прямыми сводится к определениям угла . Задача об определении угла между этими двумя прямыми сводится к определениям угла 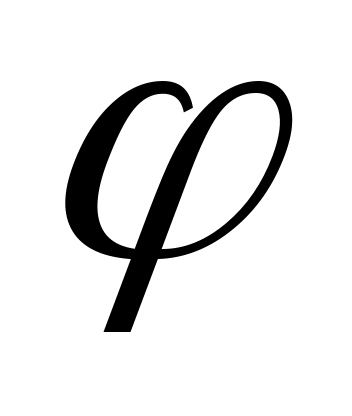 между между 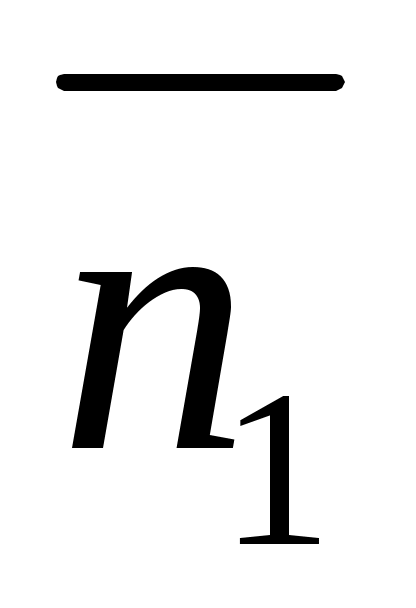 и и 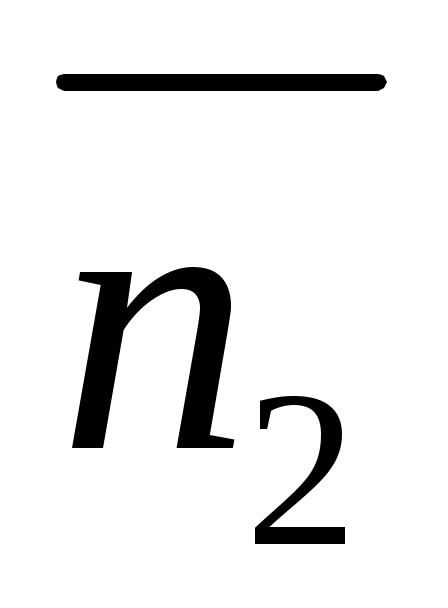 . .
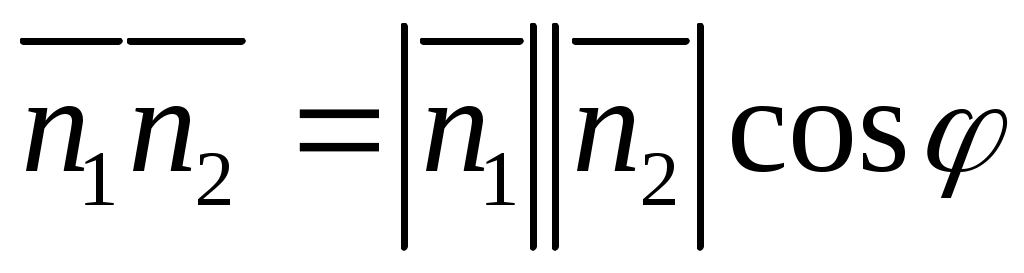 , , 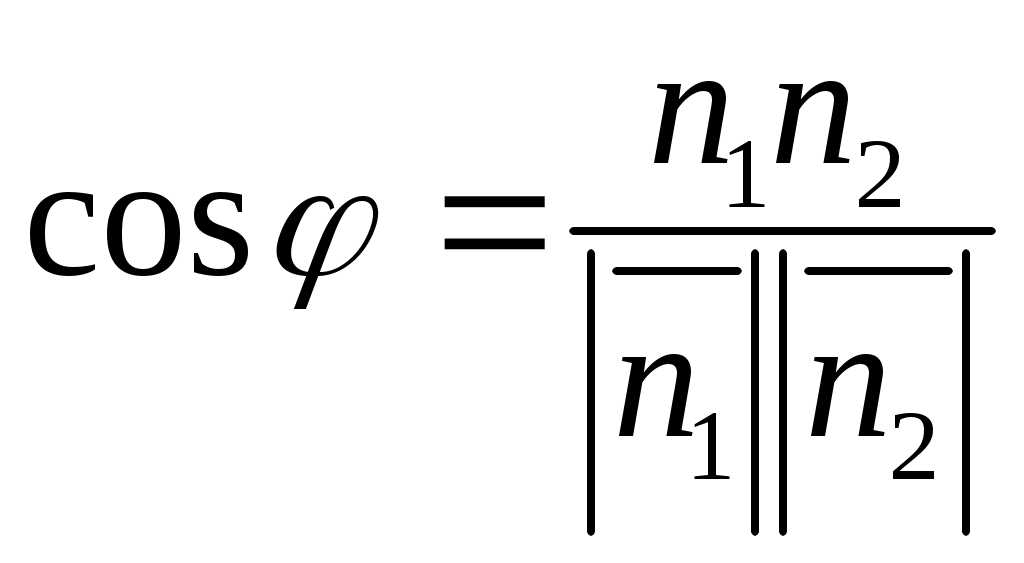 , , 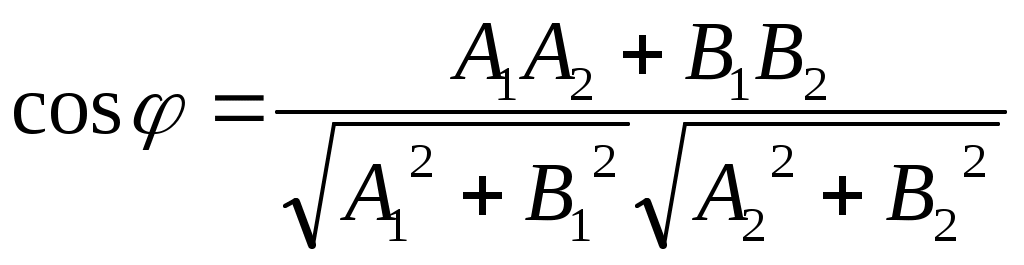
Условие параллельности 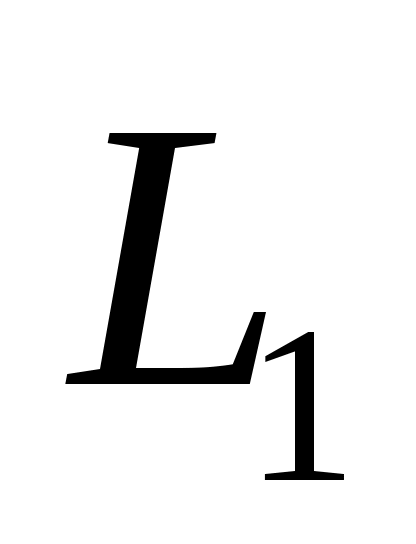 и и 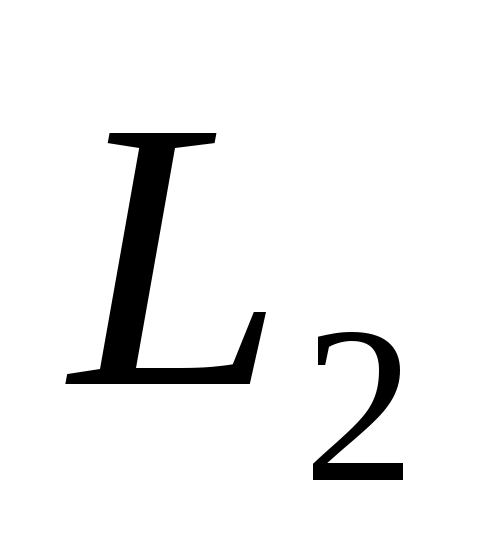 вытекает из условий коллинеарности вытекает из условий коллинеарности 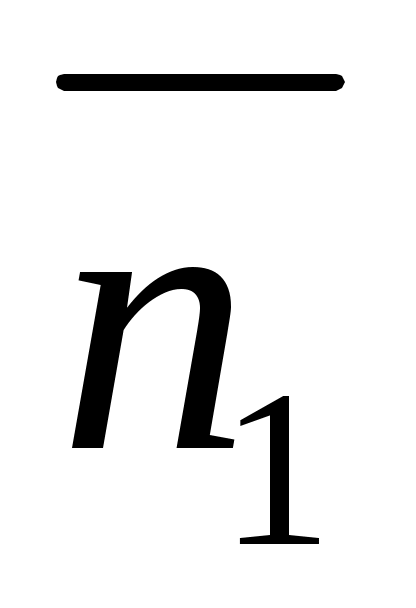 и и 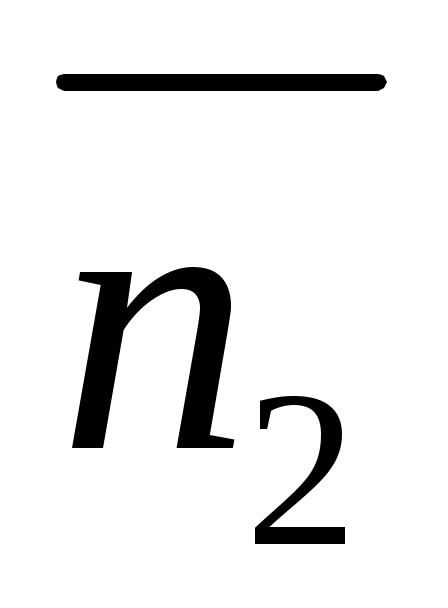
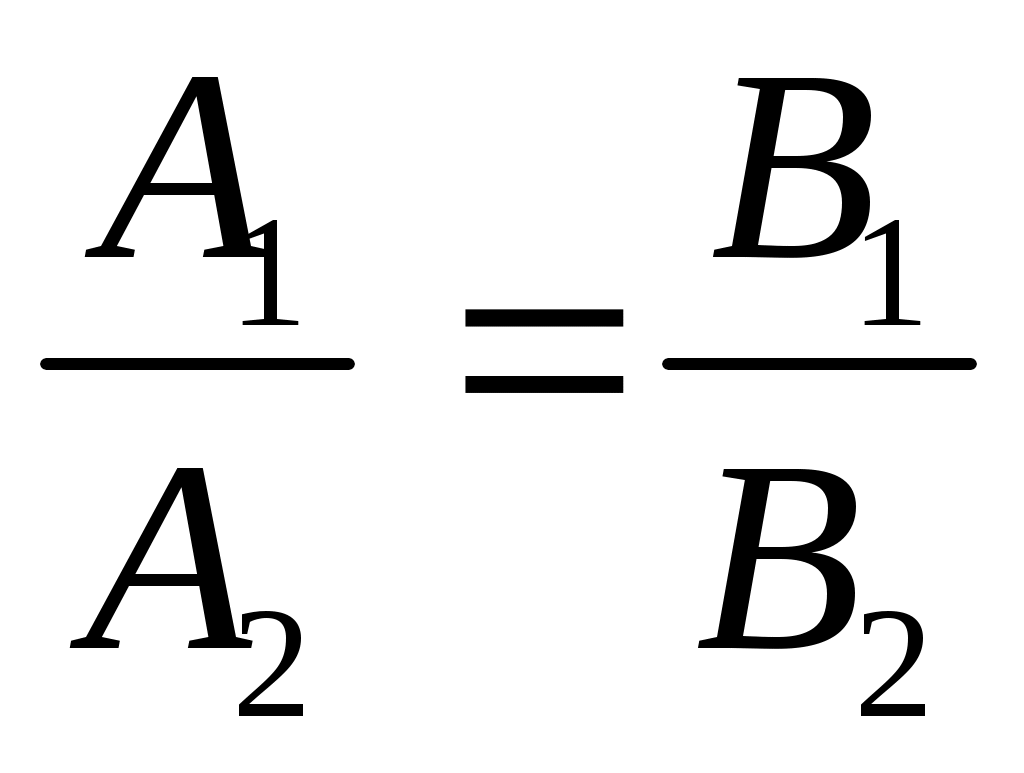 . .
Условие перпендикулярности 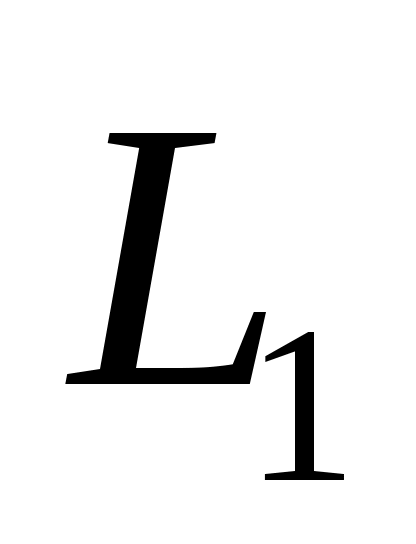 и и 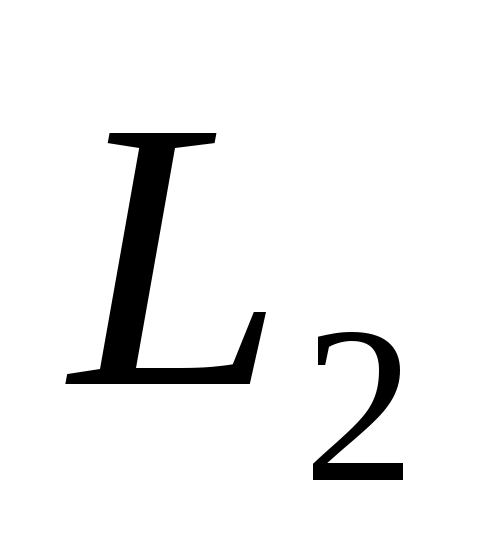 вытекает из вытекает из 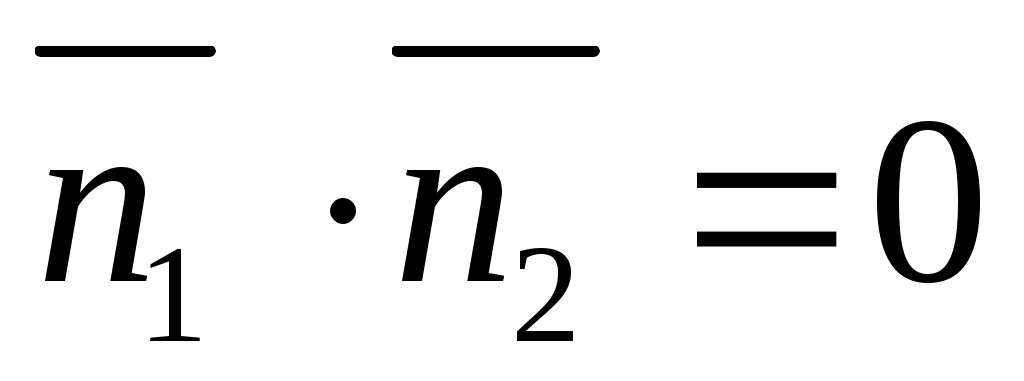
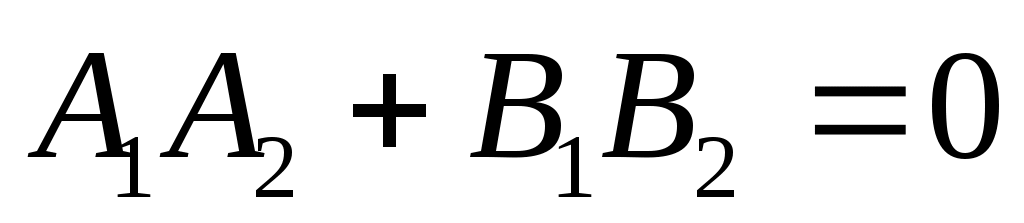 . .
б) Если две прямые 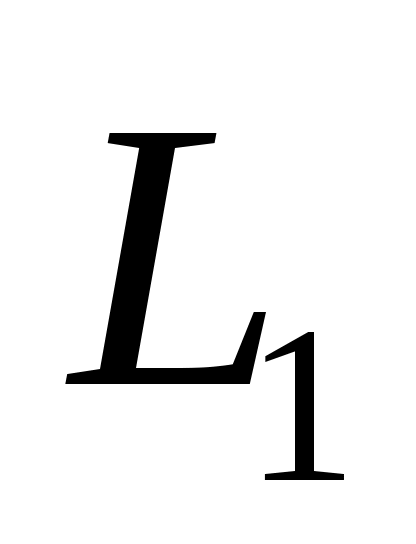 и и 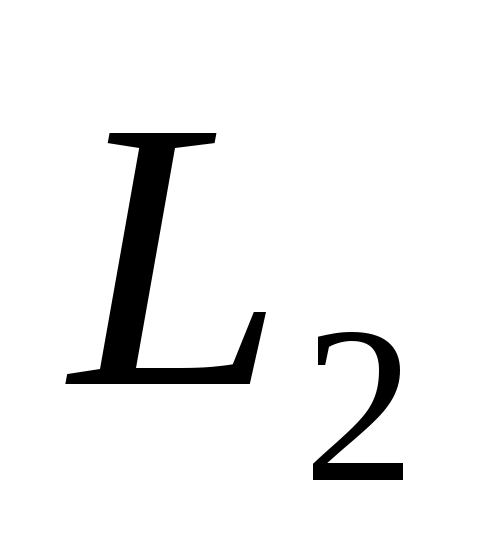 заданы уравнениями с угловыми коэффициентами заданы уравнениями с угловыми коэффициентами 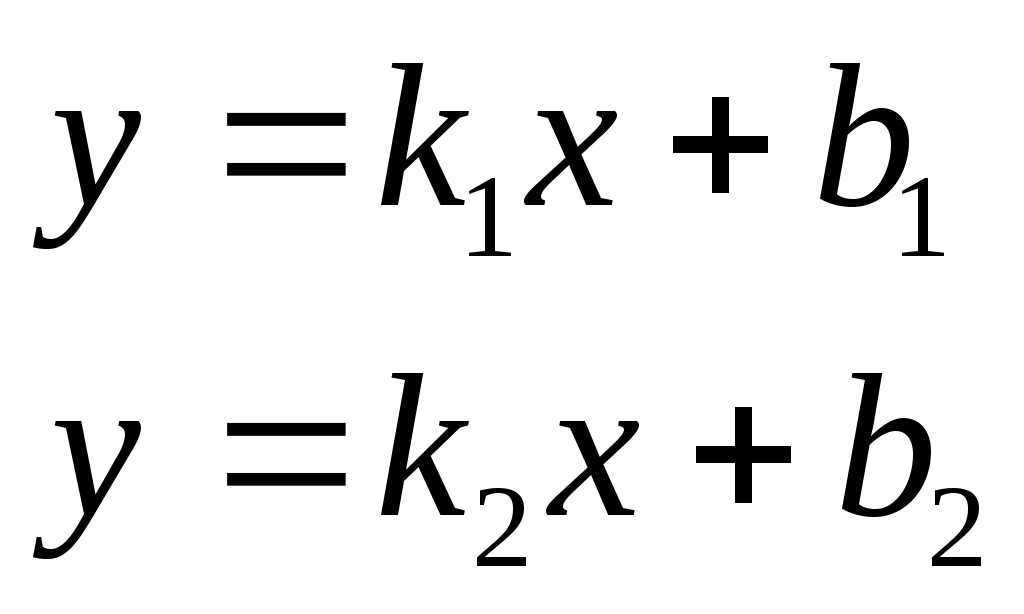
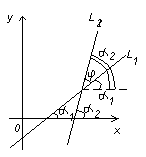
Если 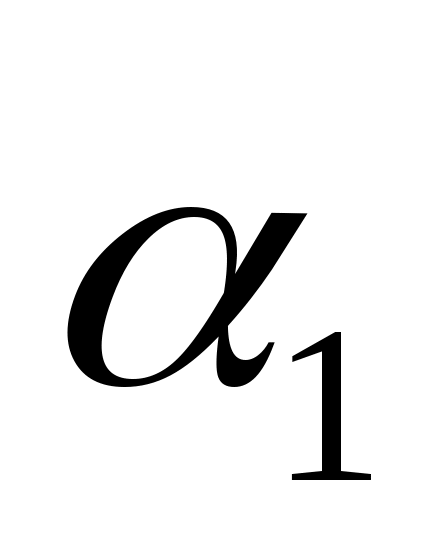 и и 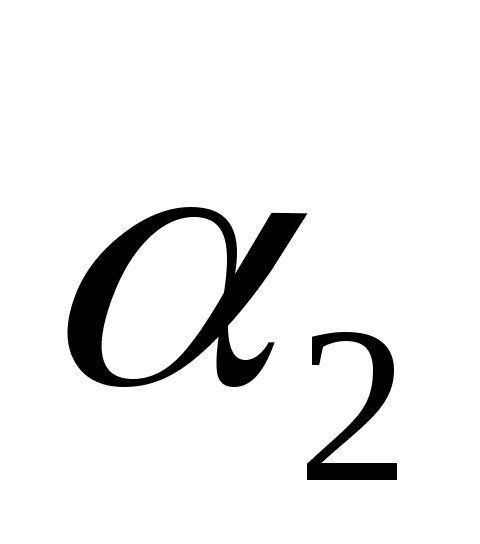 - углы наклона прямых - углы наклона прямых 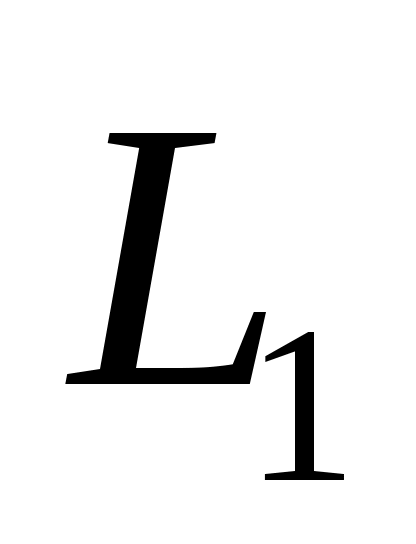 и и 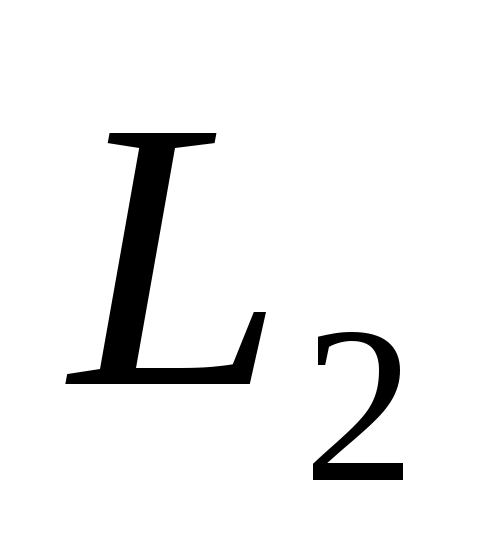 к оси к оси 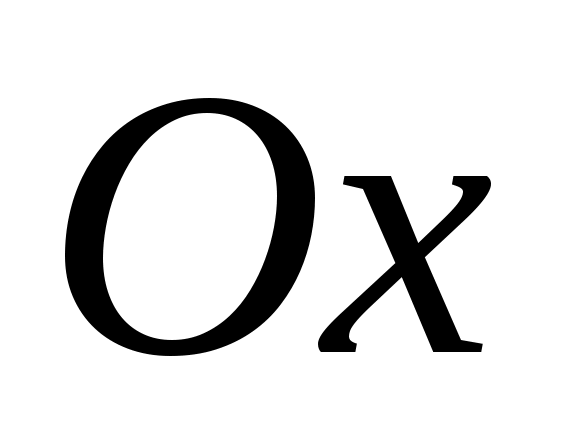 , а , а 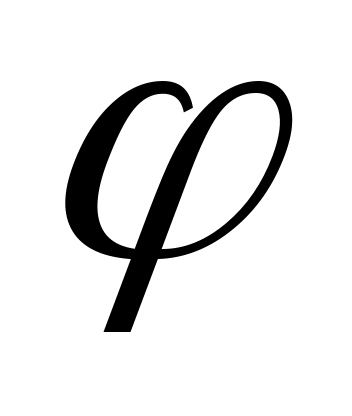 -один из углов между этими прямыми, тогда -один из углов между этими прямыми, тогда 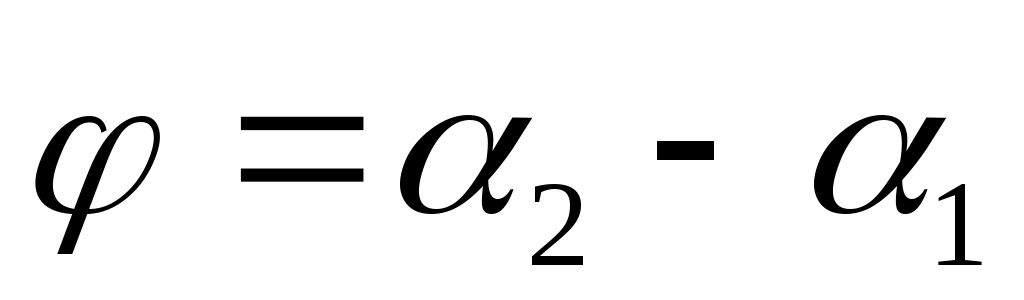 . .
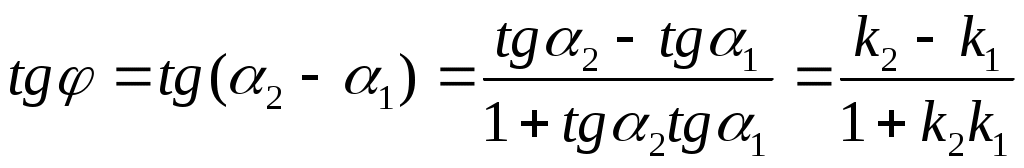
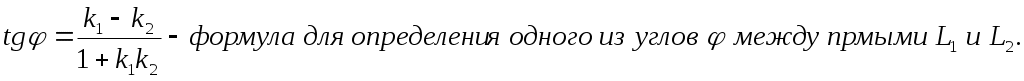
Прямые параллельны, когда тангенс угла между ними равен нулю.
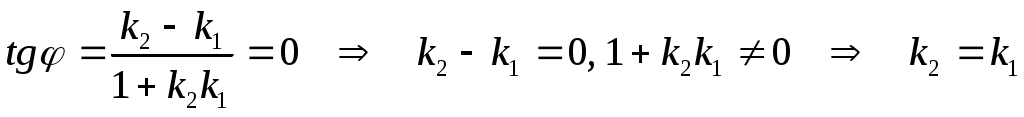 - условие параллельности двух прямых. - условие параллельности двух прямых.
Условие перпендикулярности прямых 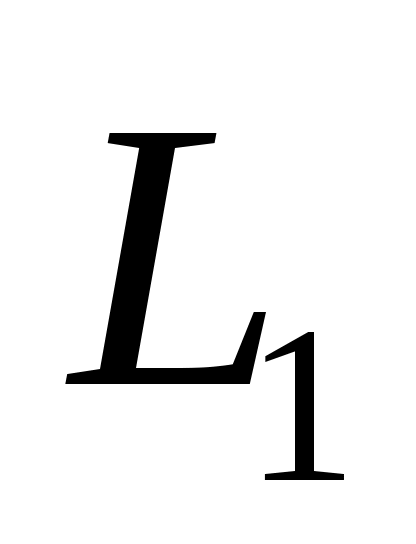 и и 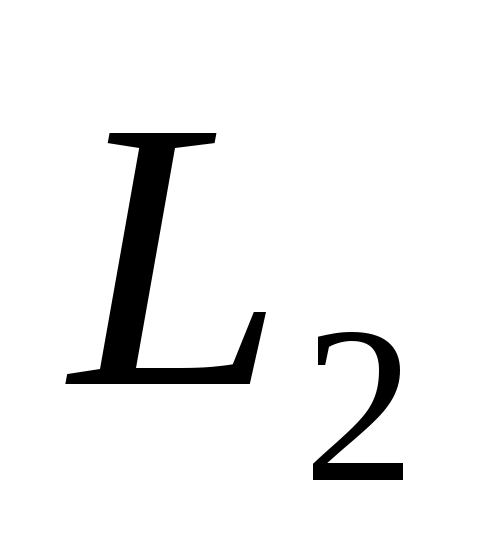 . .
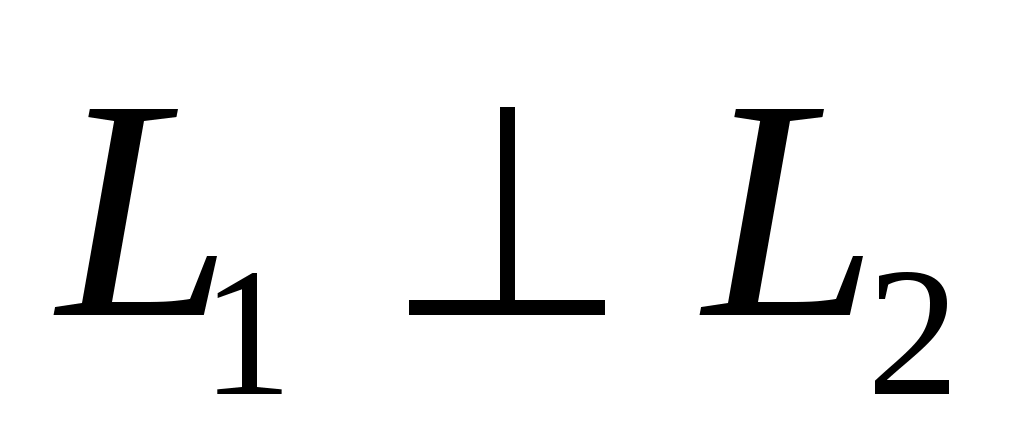 , то , то 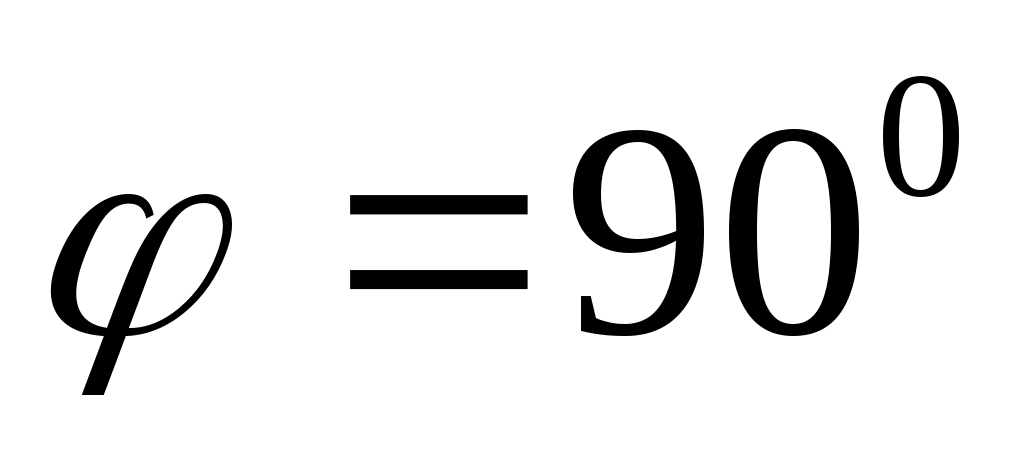 . Тангенс угла . Тангенс угла 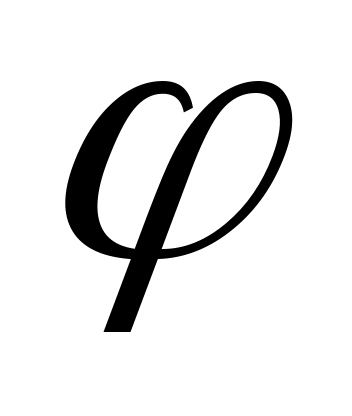 не существует. Знаменатель формулы обращается в нуль. не существует. Знаменатель формулы обращается в нуль.
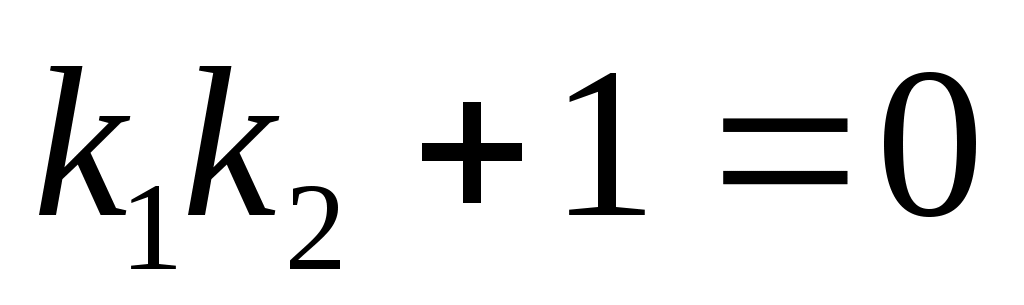
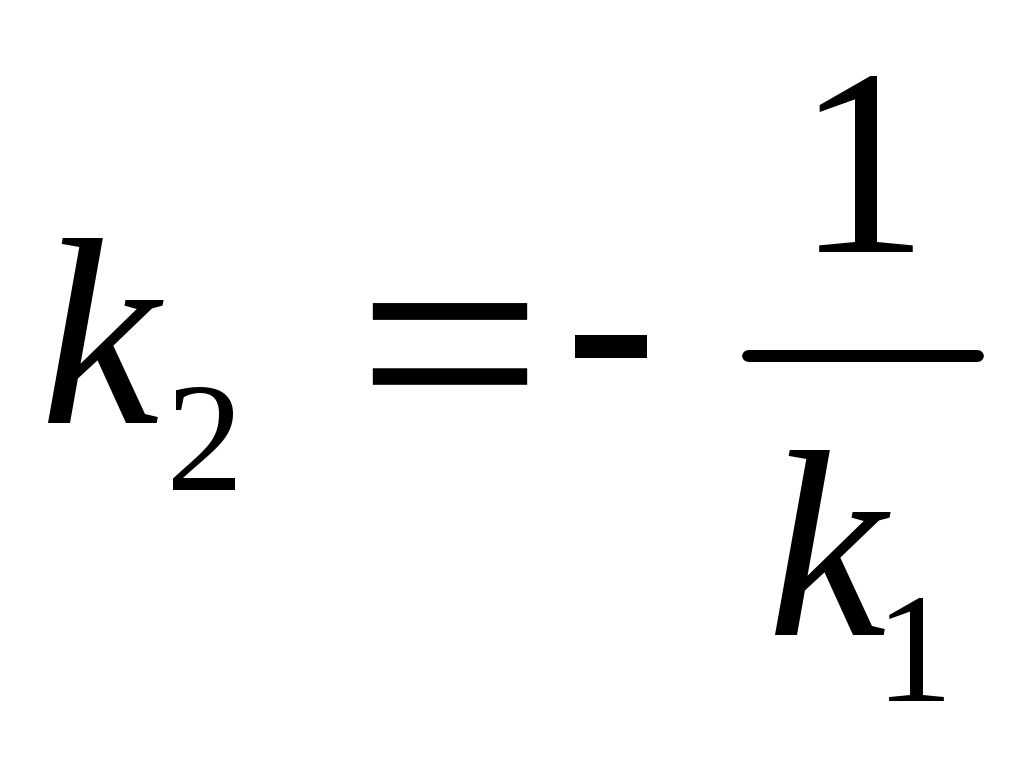 - условие перпендикулярности двух прямых. - условие перпендикулярности двух прямых.
18.Нормированное уравнение прямой. Расстояние от точки до прямой
Теорема: Если два общих уравнения 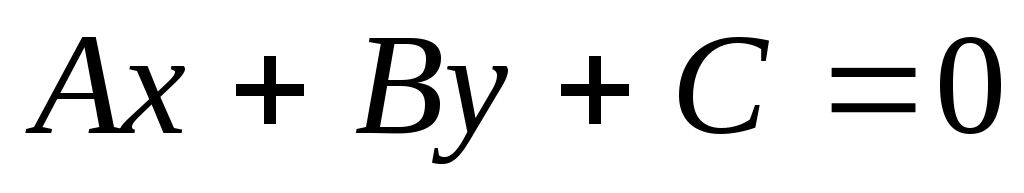 и и 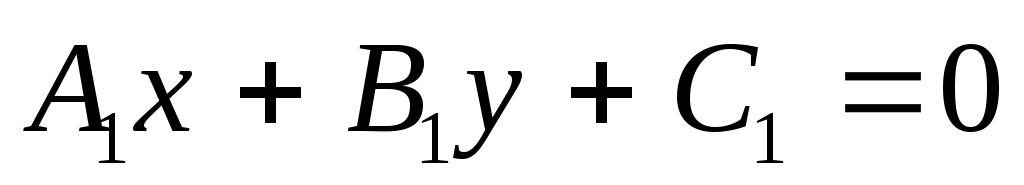 определяют одну и ту же прямую, то найдется такое число определяют одну и ту же прямую, то найдется такое число 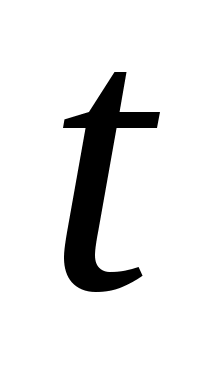 , что справедливы следующие равенства , что справедливы следующие равенства 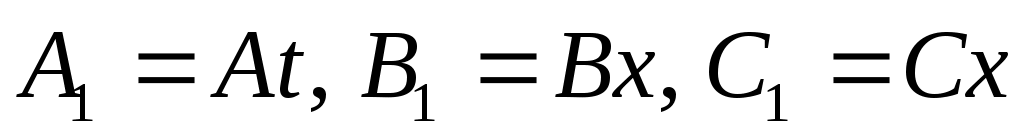
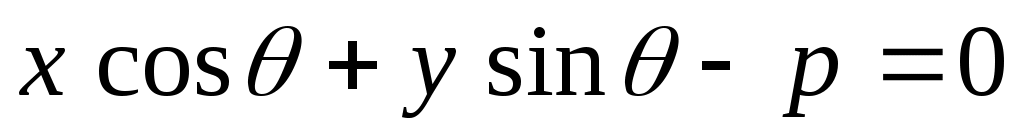 (8) , уравнение (8) называется нормированным уравнением прямой. (8) , уравнение (8) называется нормированным уравнением прямой.
Отклонение произвольной точки 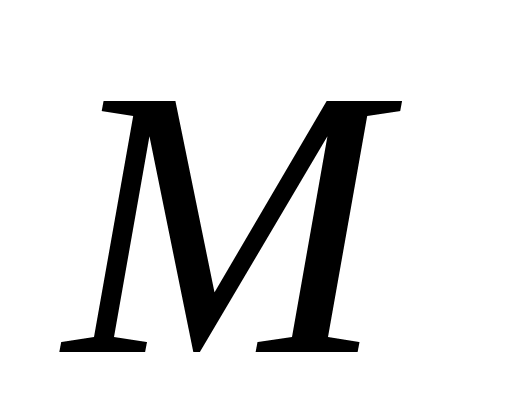 от данной прямой от данной прямой 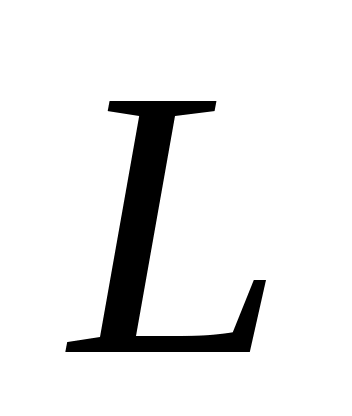 . .
П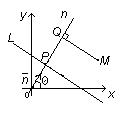 усть число усть число 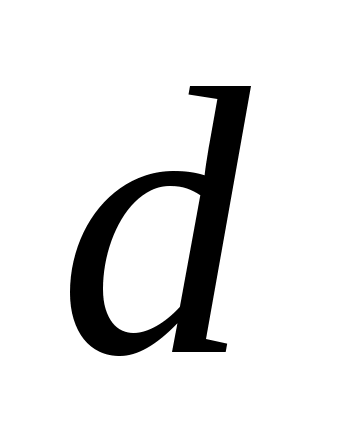 обозначает расстояние от точки обозначает расстояние от точки 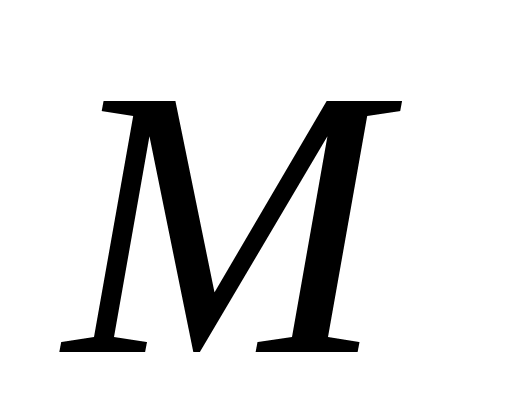 до прямой до прямой 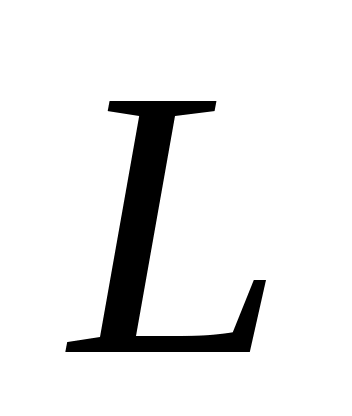 . .
Определение: Отклонением 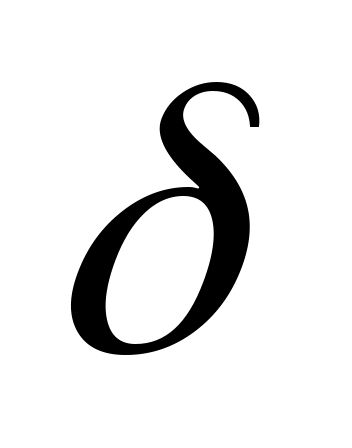 точки точки 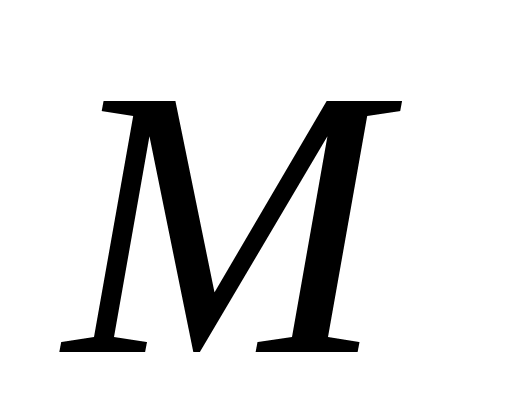 от прямой от прямой 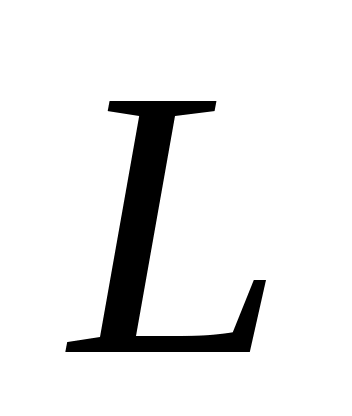 называется число называется число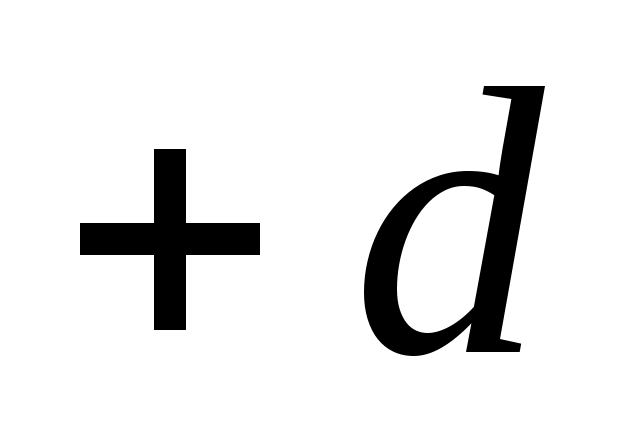 , если точка , если точка 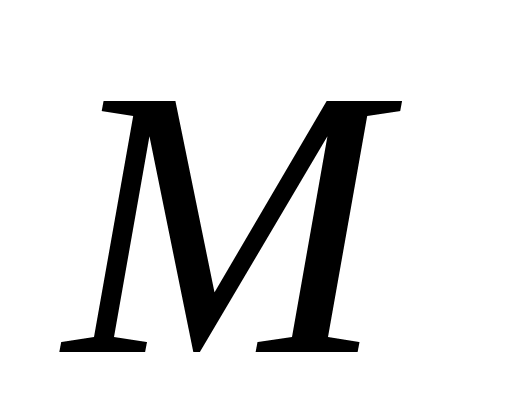 и начало координат и начало координат 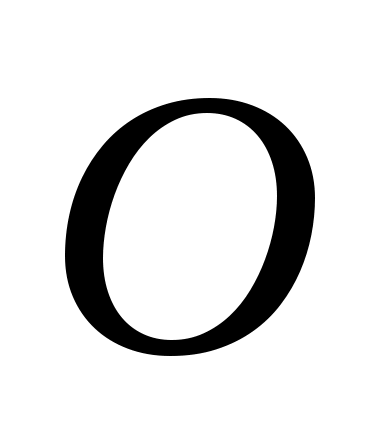 лежат по разные стороны от прямой лежат по разные стороны от прямой 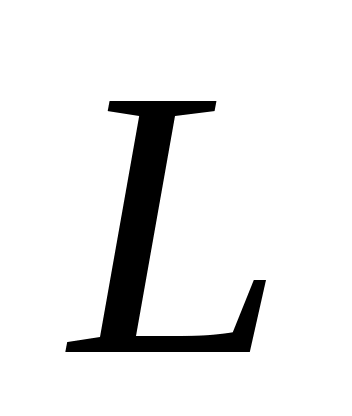 , , 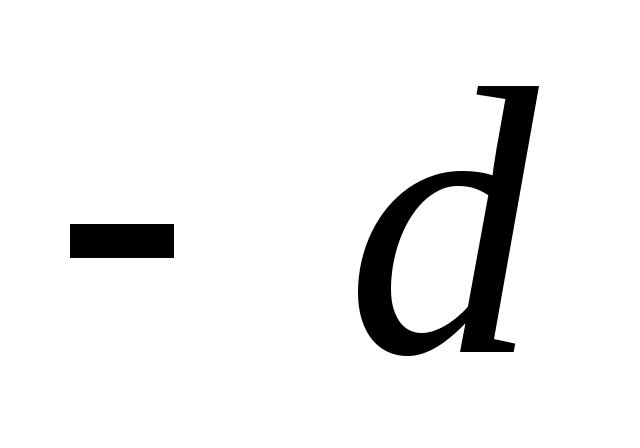 , если точка , если точка 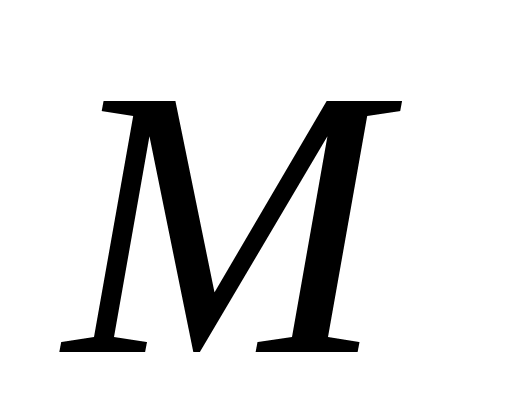 и начало координат и начало координат 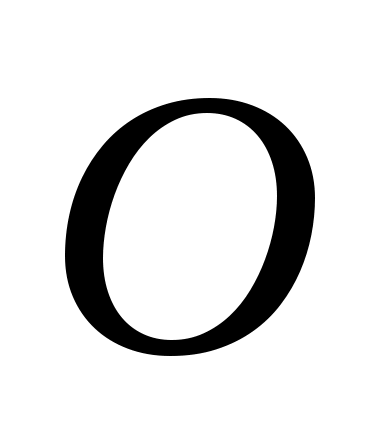 лежат по одну сторону лежат по одну сторону 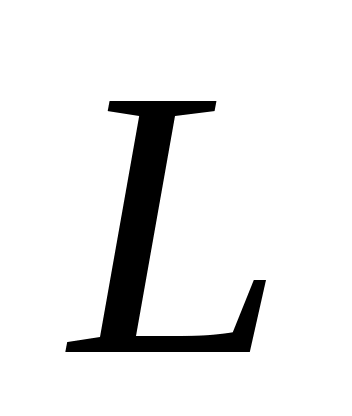 . .
Теорама: Левая часть нормированного уравнения прямой (1) равна отклонению точки 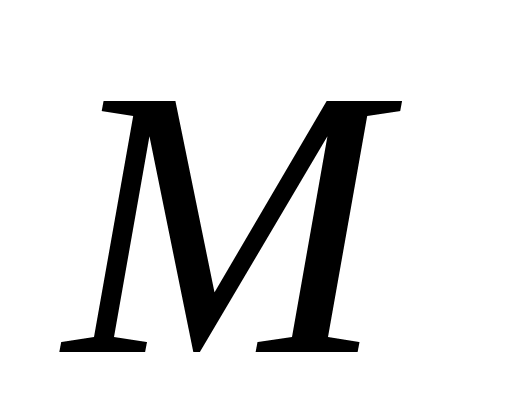 с координатами с координатами 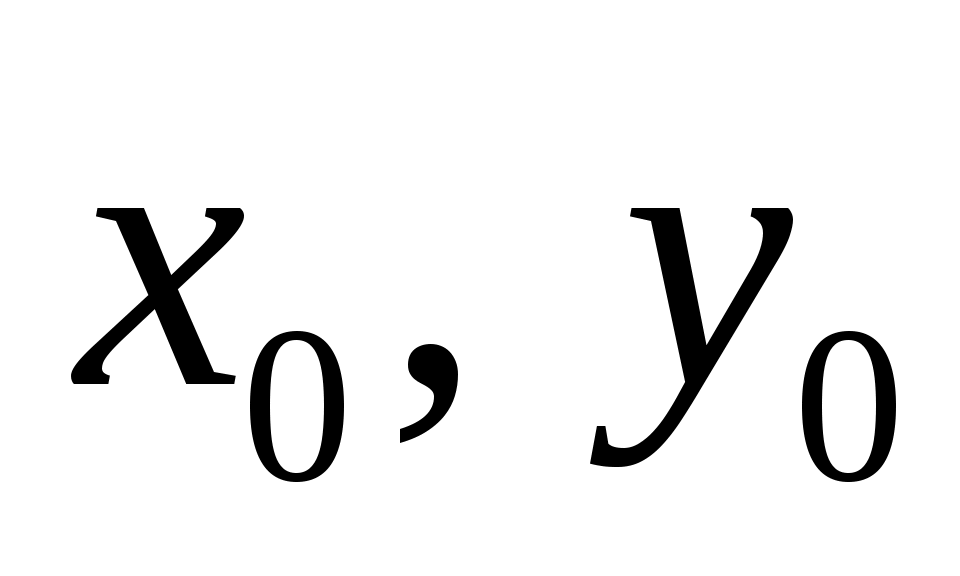 от прямой от прямой 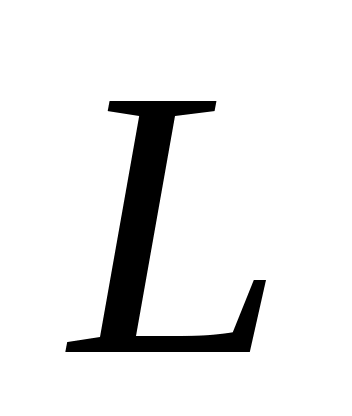 , определяемой уравнением , определяемой уравнением 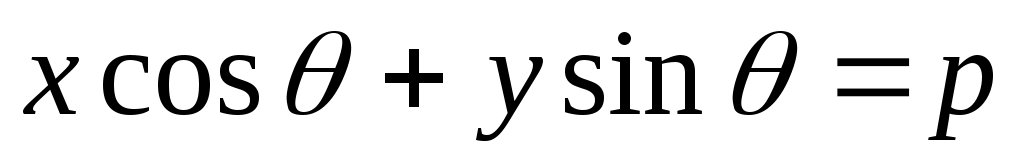 . .
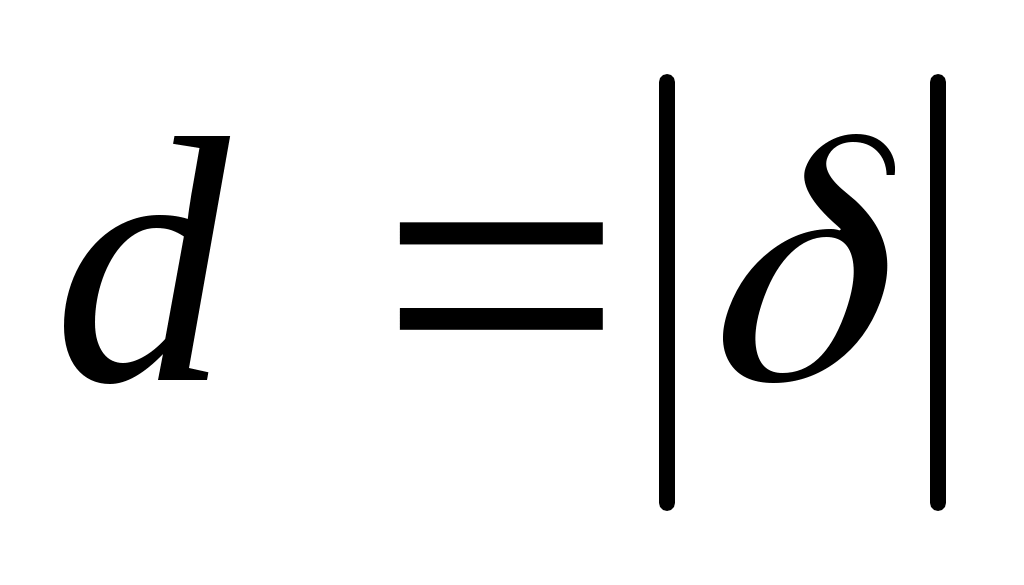
Алгоритм приведения общего уравнения прямой к нормированному виду.
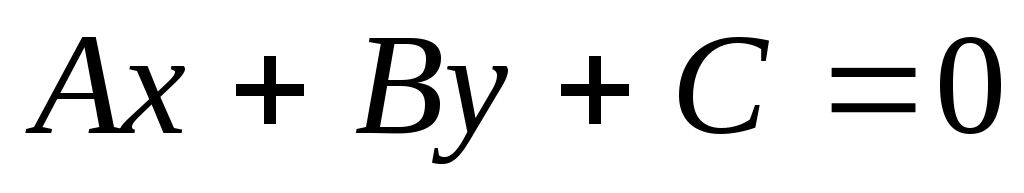 , , 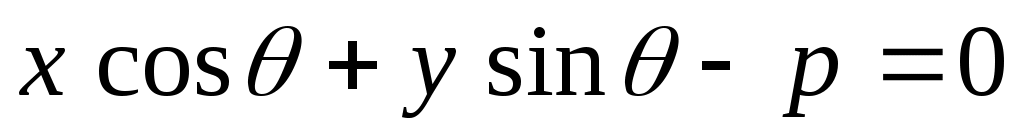 . Так как указанные уравнения должны определять одну и ту же прямую, найдется число . Так как указанные уравнения должны определять одну и ту же прямую, найдется число 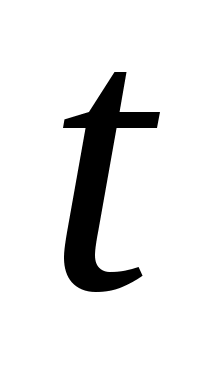 такое, что такое, что
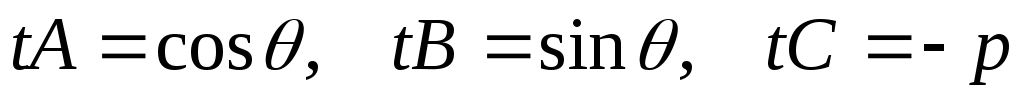 (2) (2)
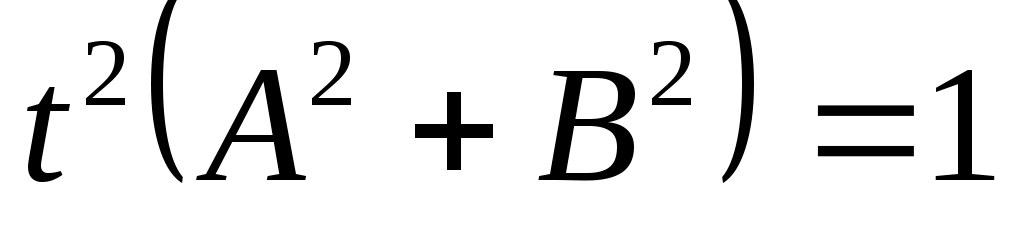 , , 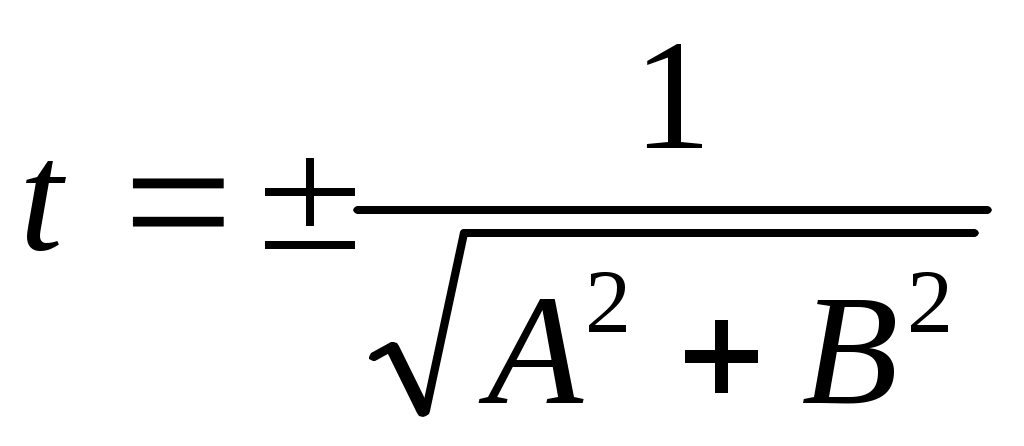 - нормирующий множитель. - нормирующий множитель.
Так как по смыслу расстояние 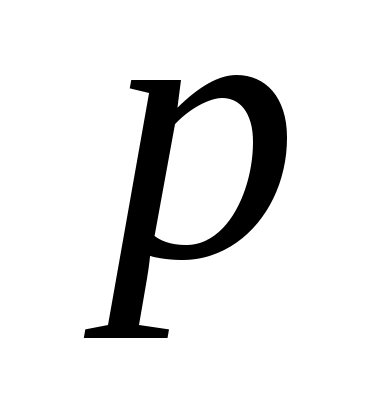 всегда неотрицательно, то из третьего равенства (2) следует, что знак всегда неотрицательно, то из третьего равенства (2) следует, что знак 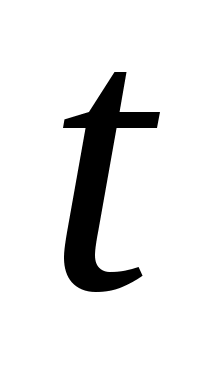 противоположен знаку противоположен знаку 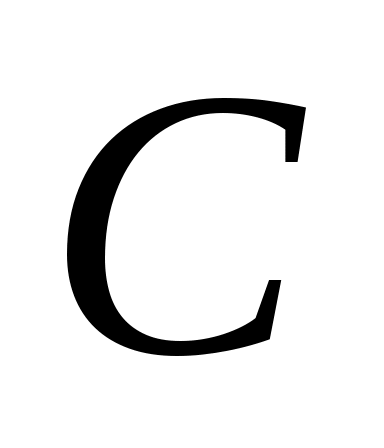 . .
Таким образом, для приведения общего уравнения прямой 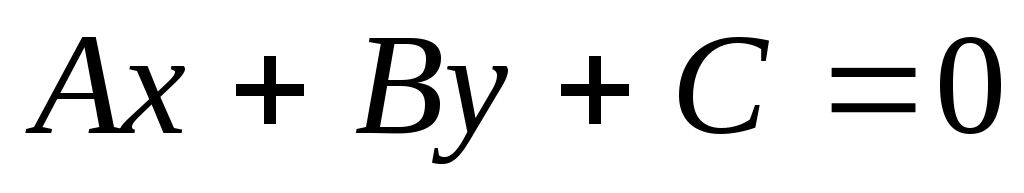 к нормированному виду следует умножить его нормирующий множитель к нормированному виду следует умножить его нормирующий множитель 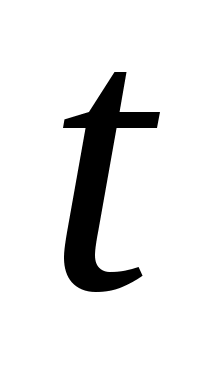 , знак которого противоположен знаку , знак которого противоположен знаку 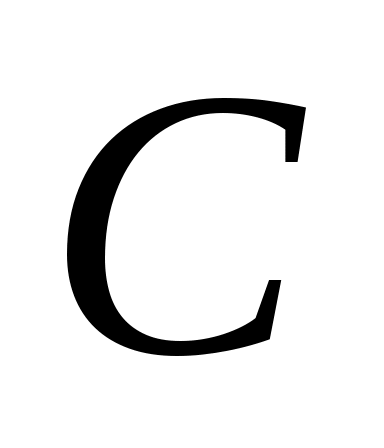 . .
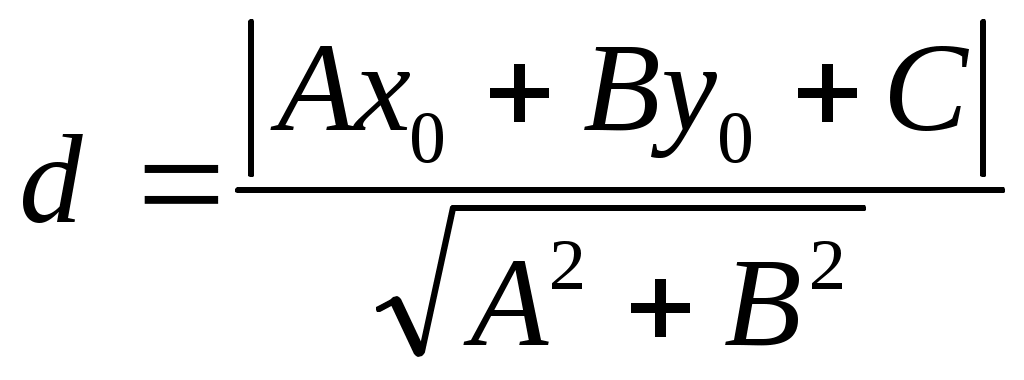 - формула для вычисления расстояния от точки до прямой. - формула для вычисления расстояния от точки до прямой.
19. Общее уравнение плоскости. Неполные уравнения плоскости. Уравнение плоскости в отрезках.
Общее уравнение плоскости
Теорема: В декартовых координатах каждая плоскость определяется уравнением первой степени.
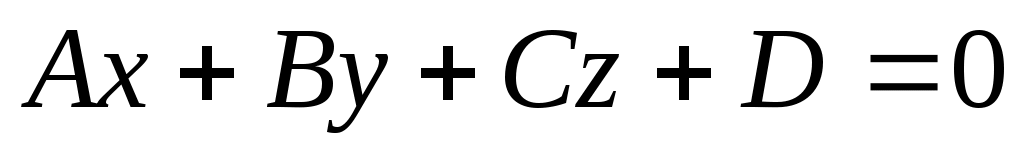 (1) Общее уравнение плоскости (1) Общее уравнение плоскости
Определение: Вектор, перпендикулярный к плоскости называется нормальным вектором плоскости 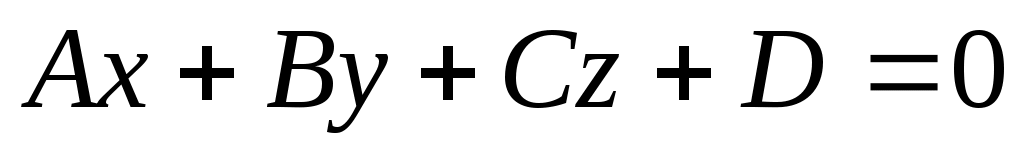 , , 
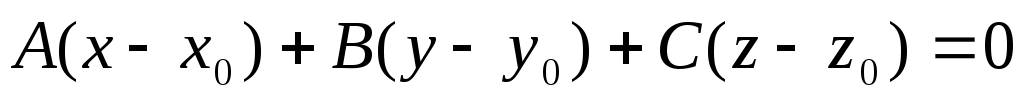 (2) - есть уравнение плоскости проходящей через точку (2) - есть уравнение плоскости проходящей через точку 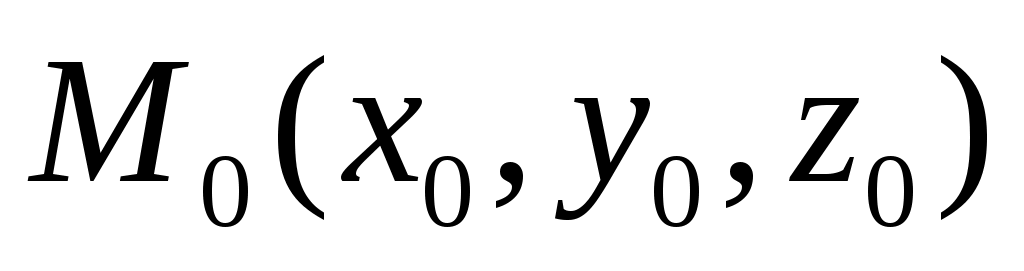 и имеющей нормальный вектор и имеющей нормальный вектор  . .
Неполные уравнения плоскости
Общее уравнение плоскости 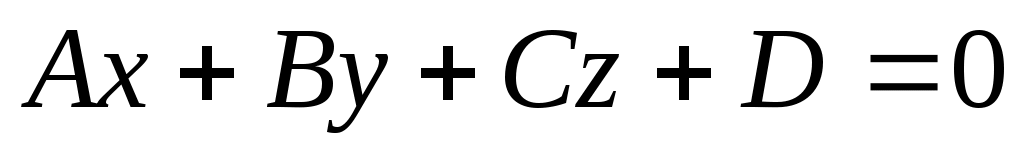 называется полным, если все его коэффициенты называется полным, если все его коэффициенты 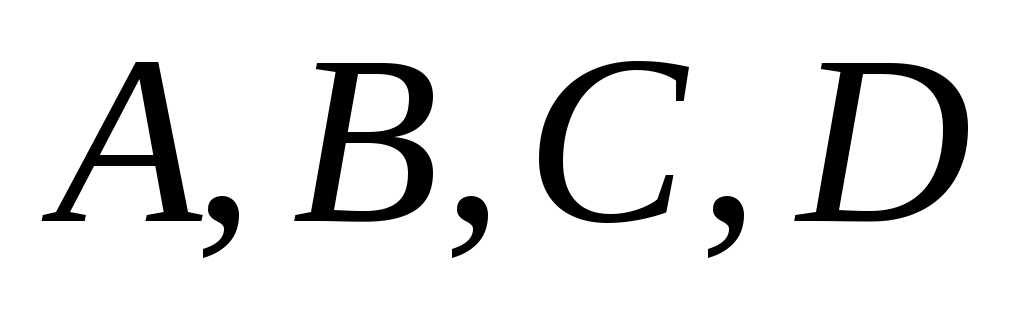 отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение называется неполным. отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение называется неполным.
Различные виды неполных уравнений.
1) Если 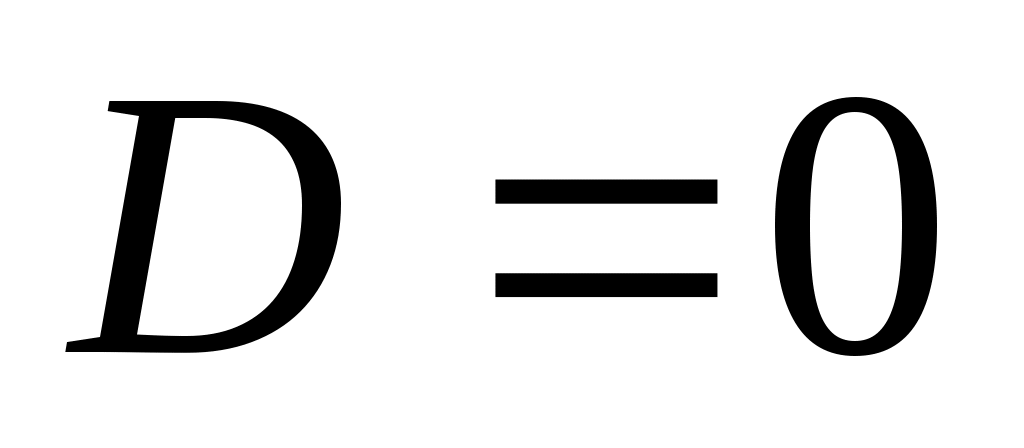 ,тогда ,тогда 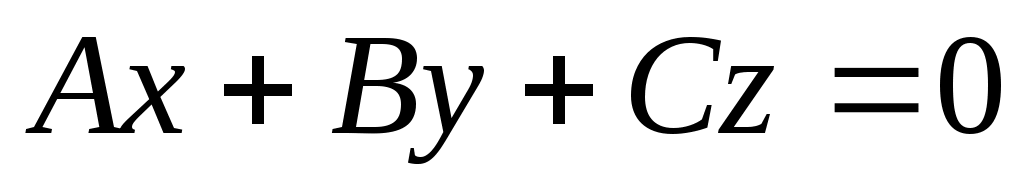 , определяет плоскость, проходящую через начало координат. , определяет плоскость, проходящую через начало координат.
2) Если  , тогда , тогда 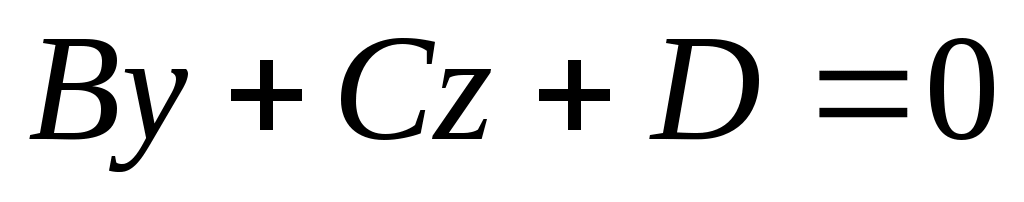 , определяет плоскость параллельную оси , определяет плоскость параллельную оси 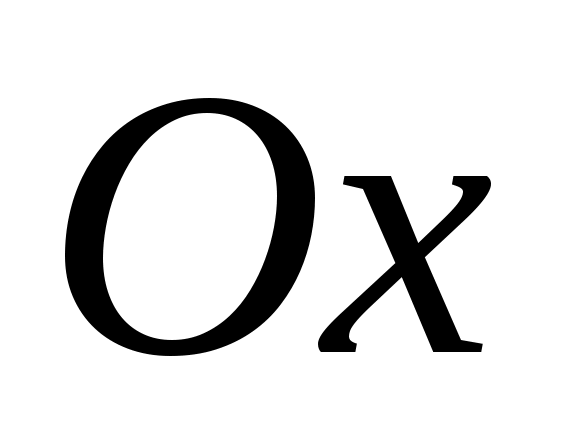 . .
3) Если 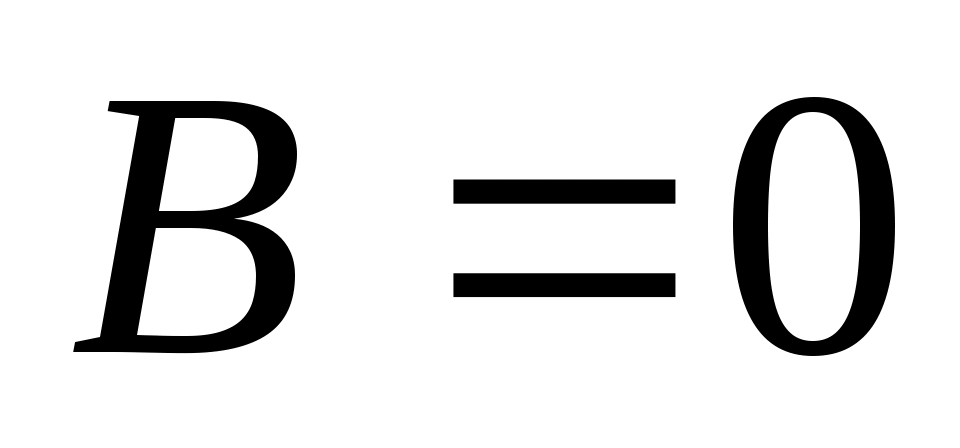 , тогда , тогда 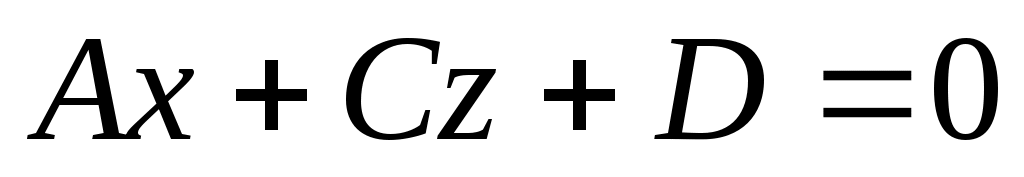 , определяет плоскость параллельную оси , определяет плоскость параллельную оси 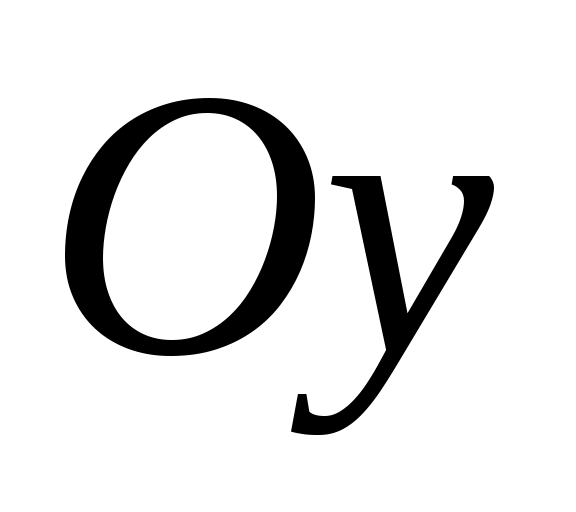 . .
4) Если 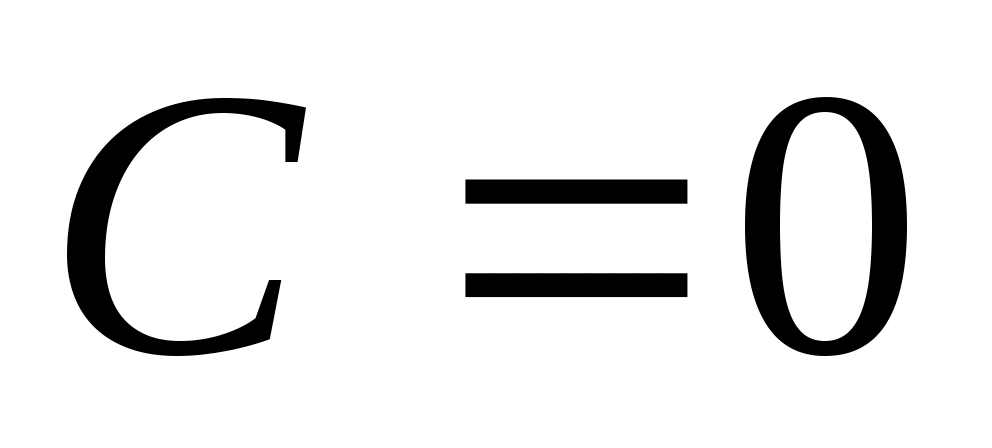 , тогда , тогда 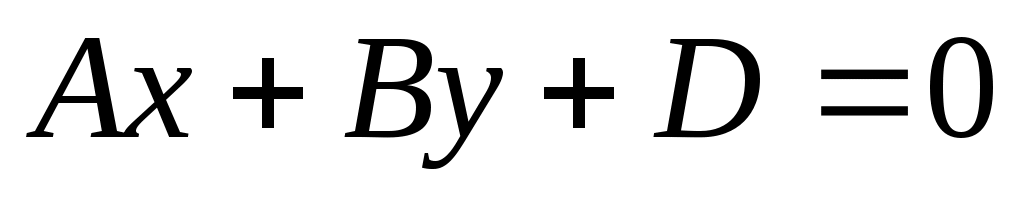 определяет плоскость параллельную оси определяет плоскость параллельную оси  . .
5) Если 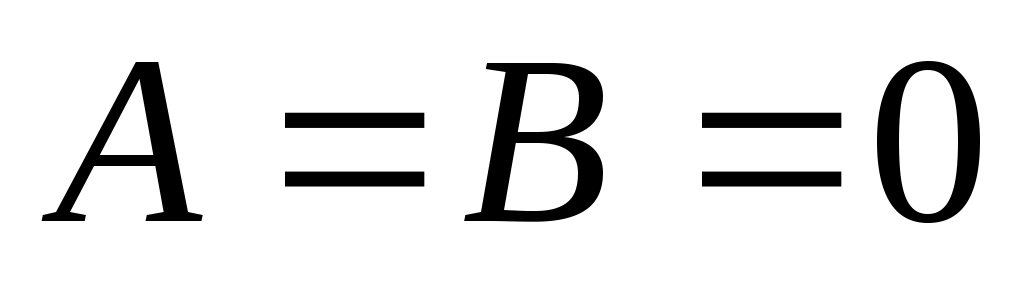 , тогда , тогда 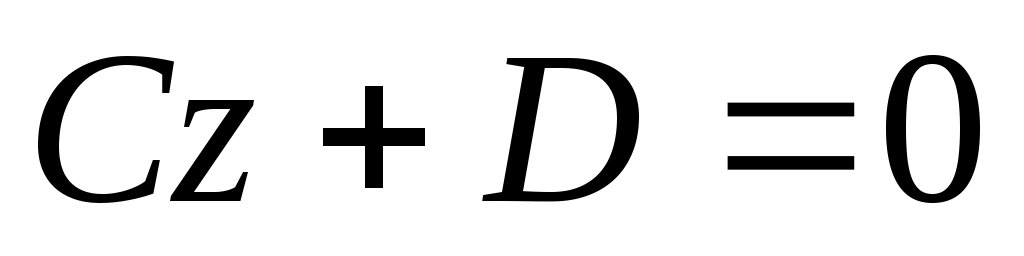 , определяет плоскость параллельную координатной плоскости , определяет плоскость параллельную координатной плоскости 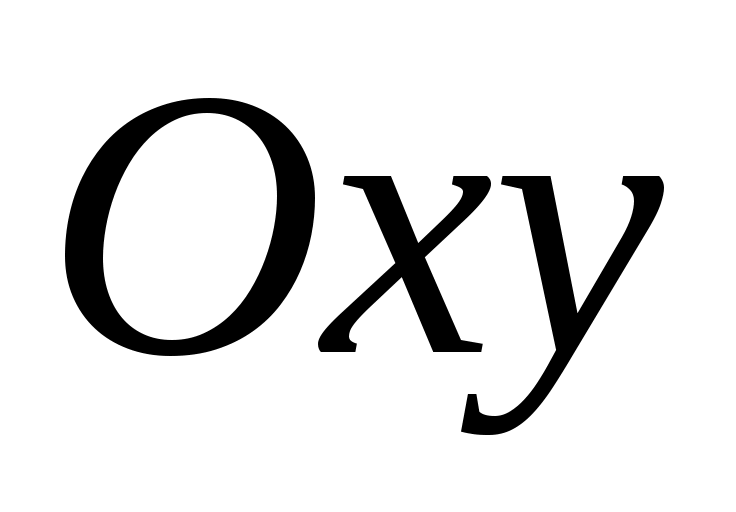 (либо параллельна осям (либо параллельна осям 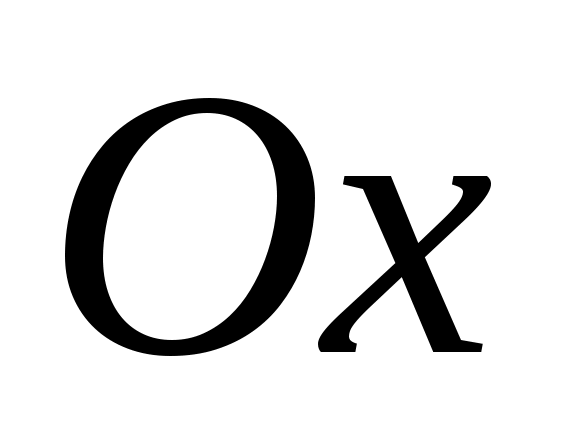 и и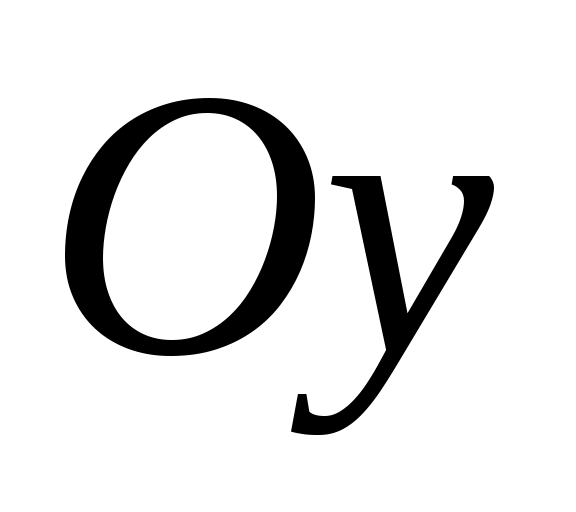 ). ).
6) 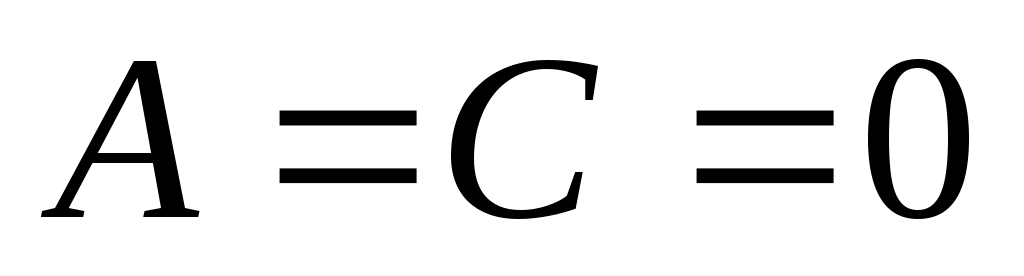 , тогда , тогда 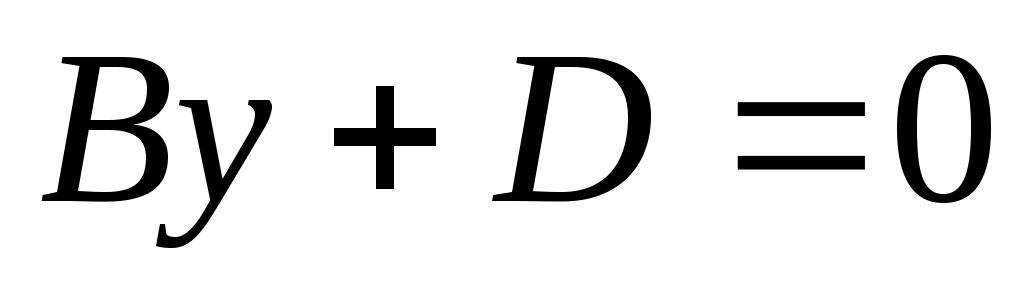 параллельна оси параллельна оси 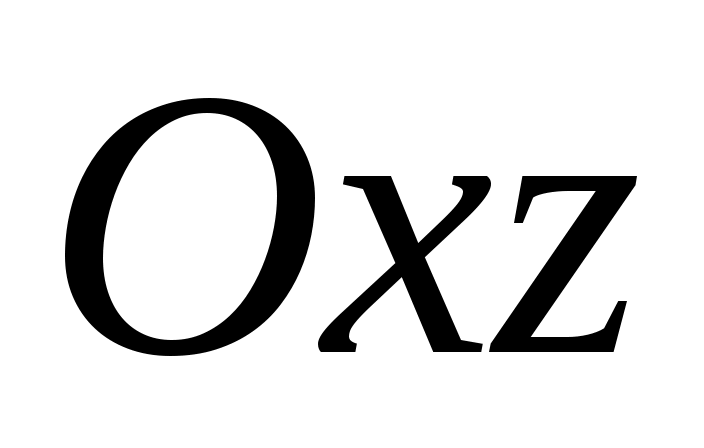 . .
7) 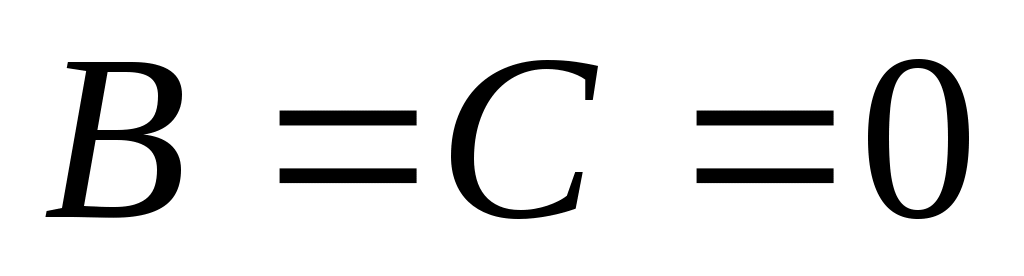 , тогда , тогда 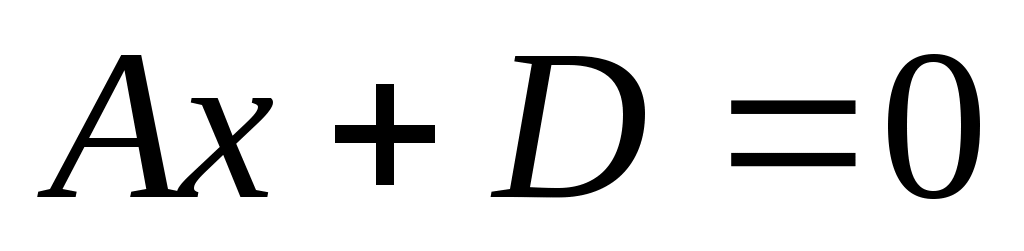 параллельна оси параллельна оси  . .
8 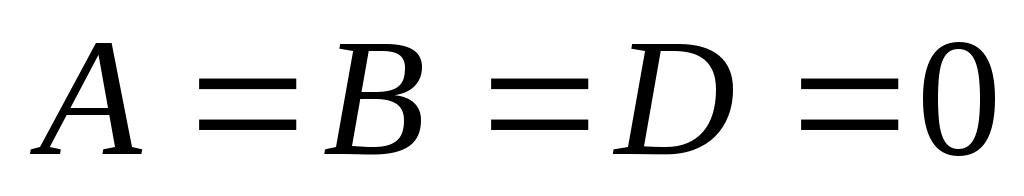 , тогда , тогда 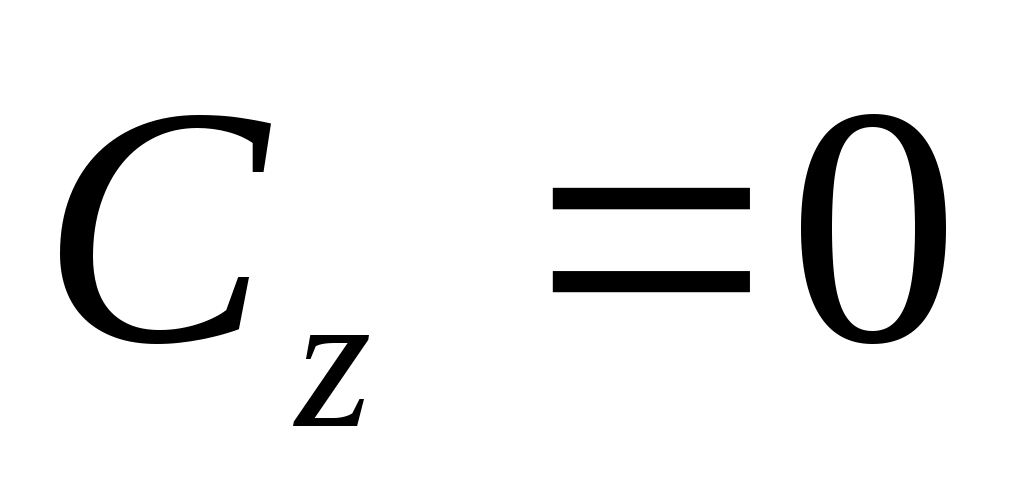 определяет координатную плоскость определяет координатную плоскость 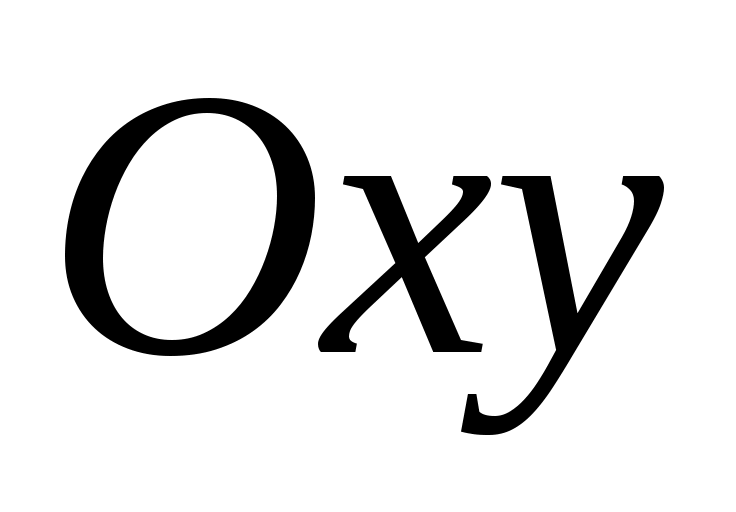 . .
9) 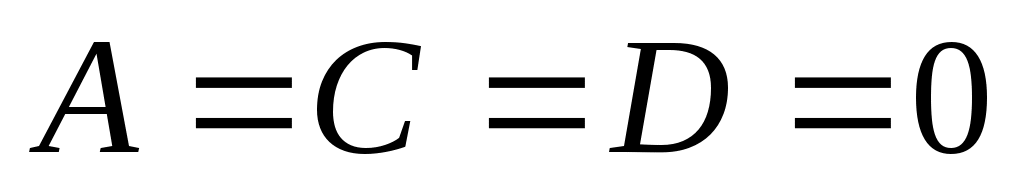 , тогда , тогда 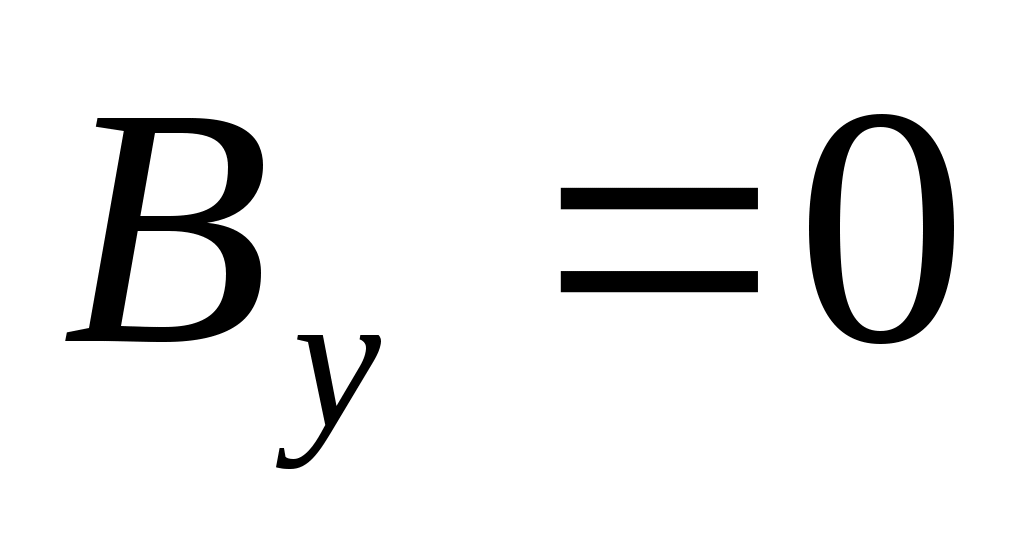 определяет координатную плоскость определяет координатную плоскость 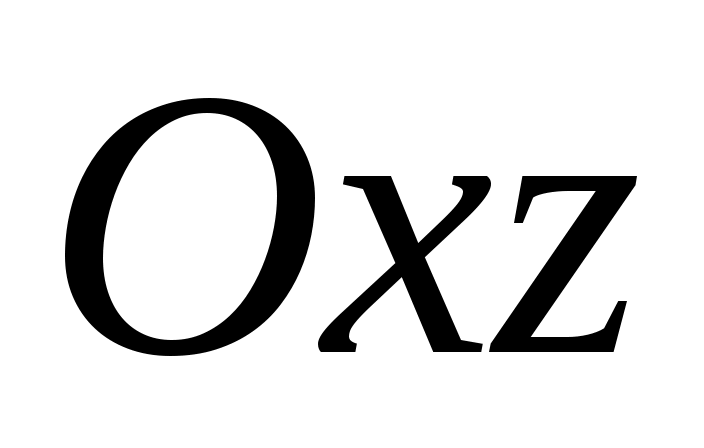 . .
10) 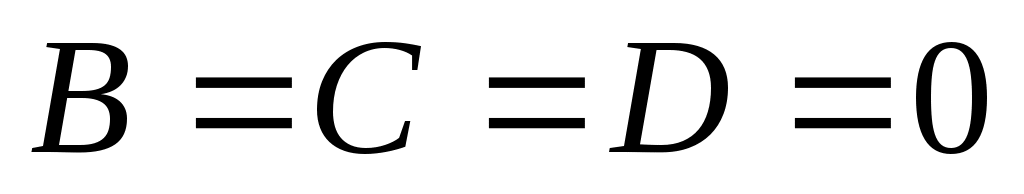 , тогда , тогда 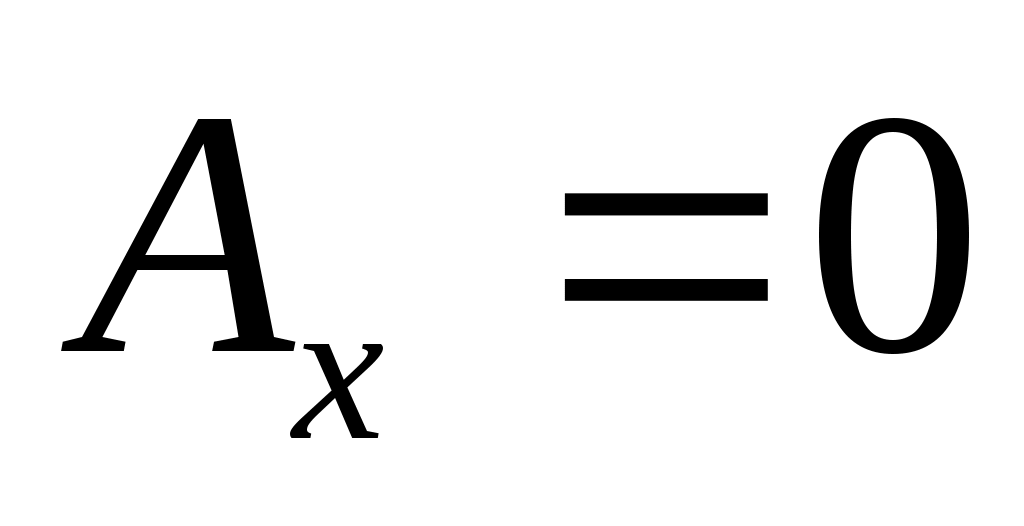 определяет координатную плоскость определяет координатную плоскость  . .
Уравнение плоскости «в отрезках». Рассмотрим общее уравнение (1). Уравнение
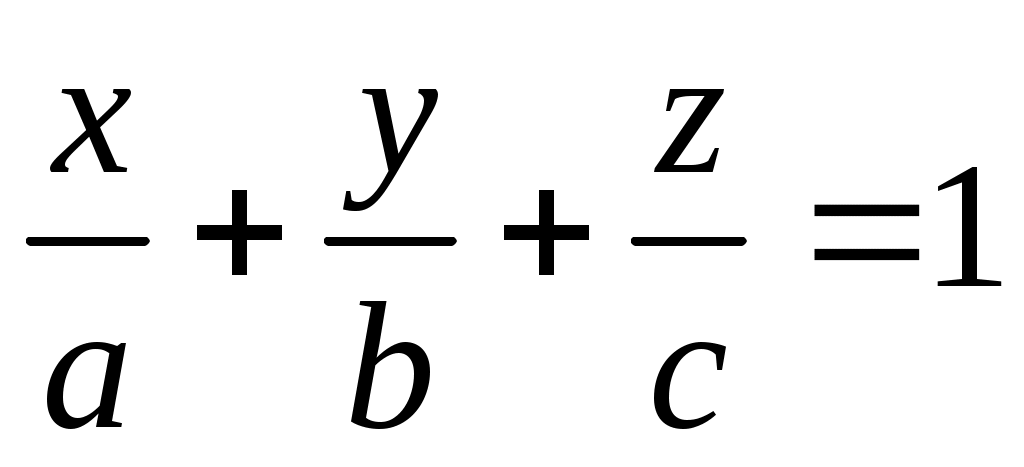 (3) - называется уравнением плоскости «в отрезках». (3) - называется уравнением плоскости «в отрезках».
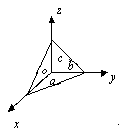
В уравнении (3) числа а, в и с имеют простой геометрический
смысл: они равны величинами отрезков, которые отсекают
плоскость на осях 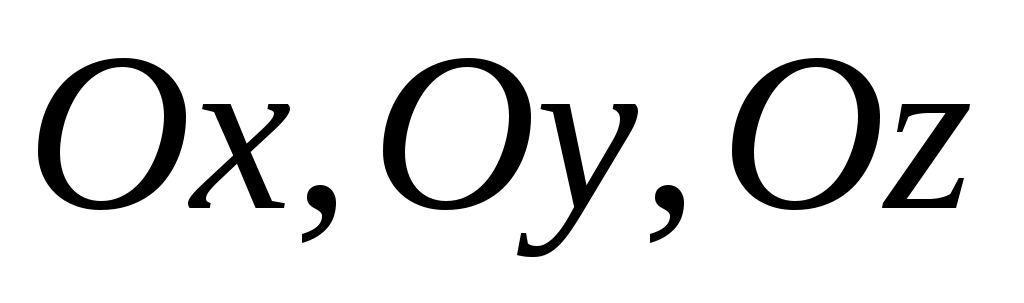 соответственно. соответственно.
Отрезки отсчитываются от начала координат.
20.Уравнение плоскости проходящей через три различные точки не лежащие на одной прямой
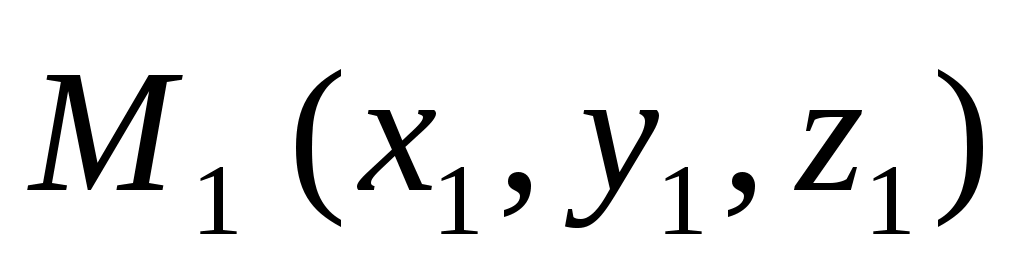 , , 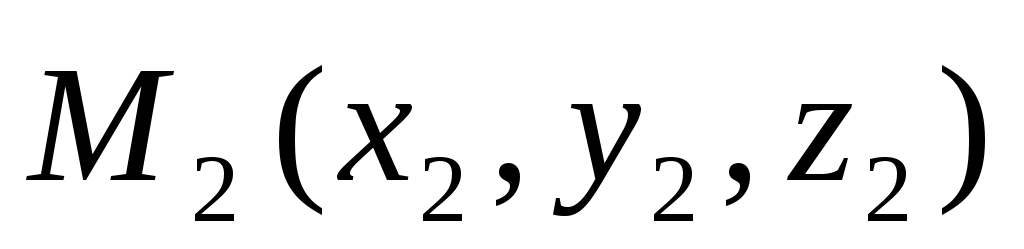 , ,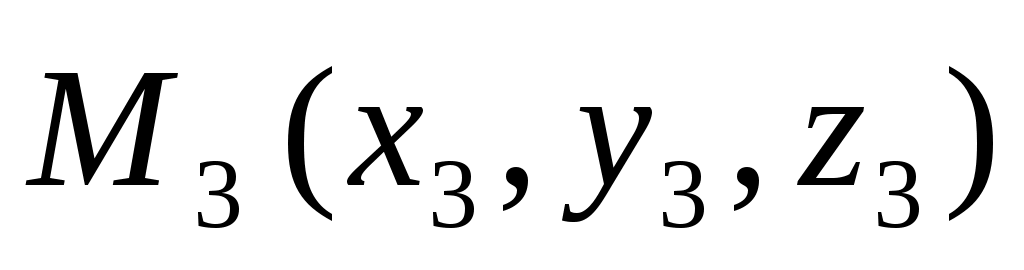 -данные точки. -данные точки. 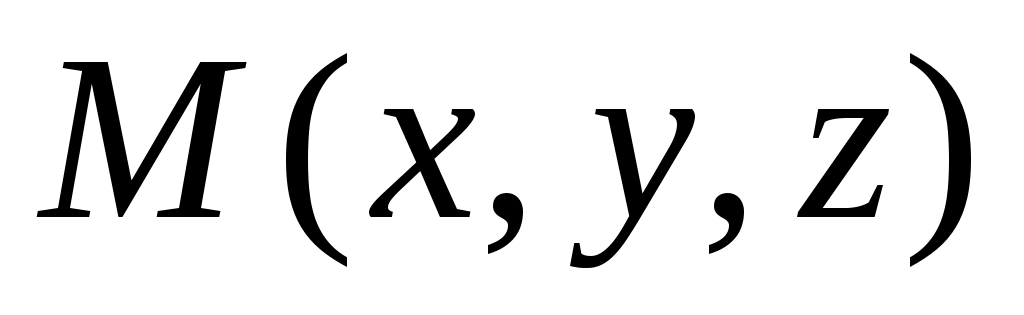 – произвольная точка плоскости. – произвольная точка плоскости.
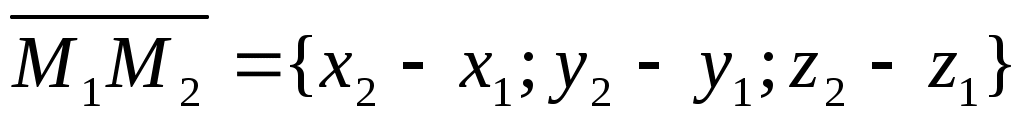
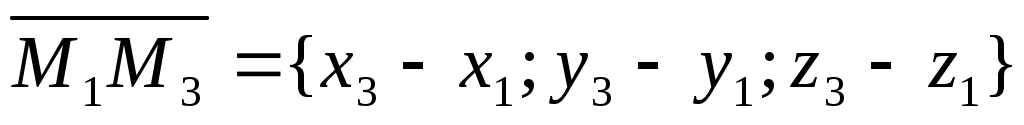
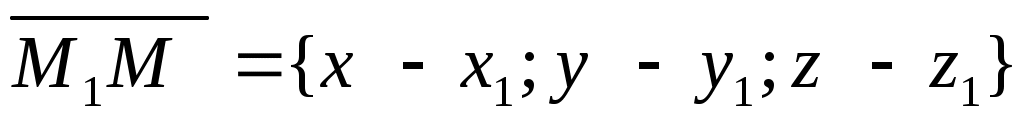
Точка 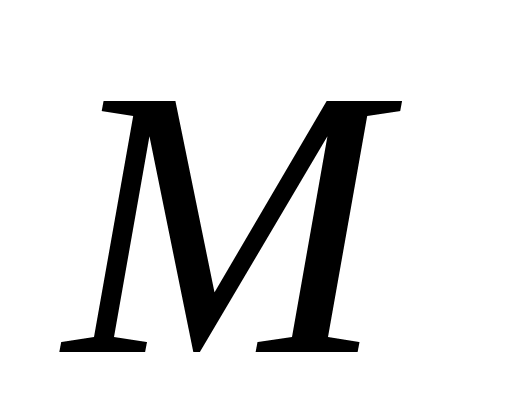 лежит в одной плоскости с точками лежит в одной плоскости с точками  тогда и только тогда, когда векторы тогда и только тогда, когда векторы , , 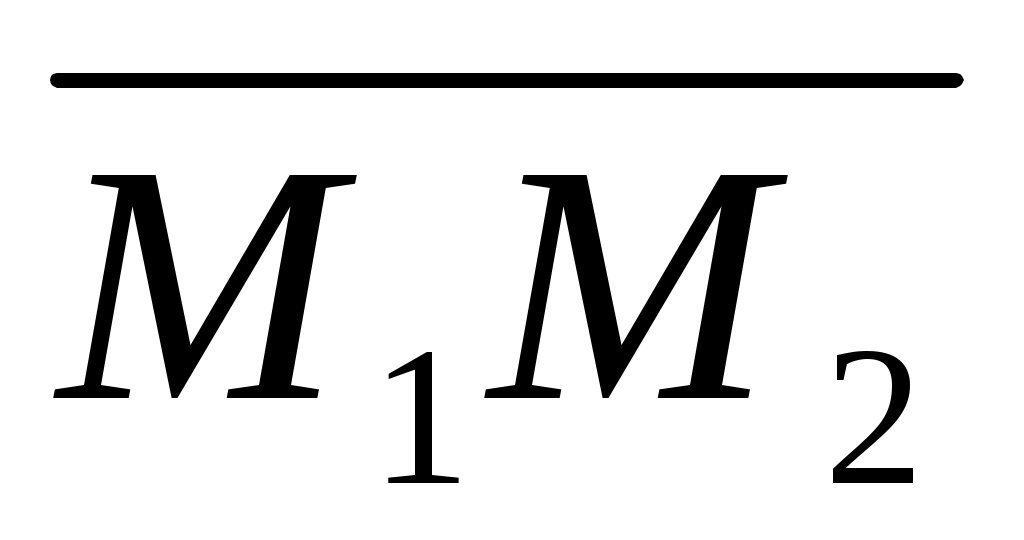 , , 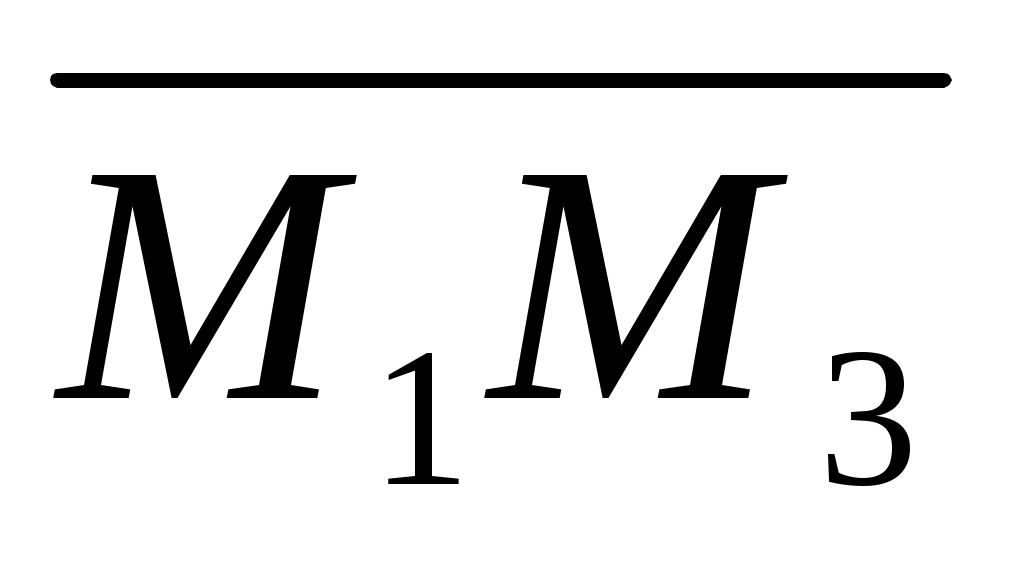 - компланарны. - компланарны.
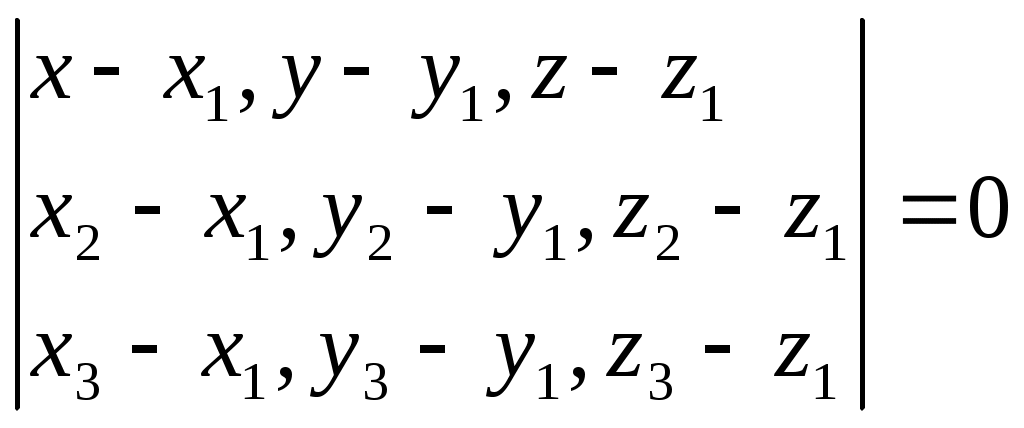 (4) - уравнение плоскости проходящей через три различные точки не лежащие на одной прямой. (4) - уравнение плоскости проходящей через три различные точки не лежащие на одной прямой.
20 Угол между двумя плоскостями.
Пусть две плоскости 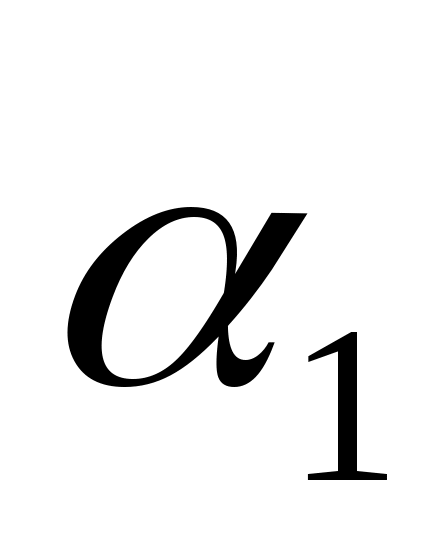 и и 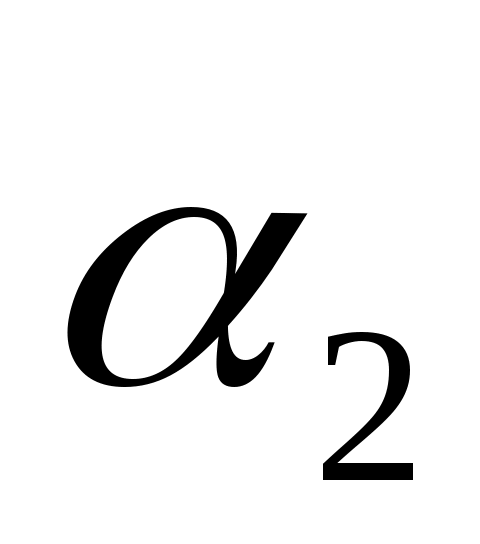 заданы общими уравнениями. заданы общими уравнениями.
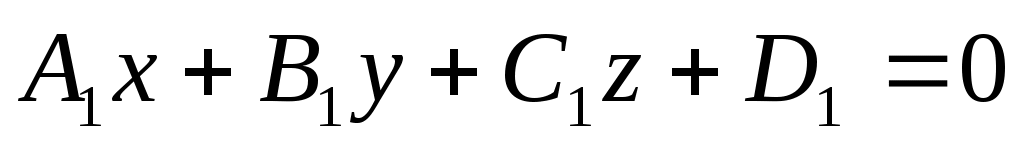 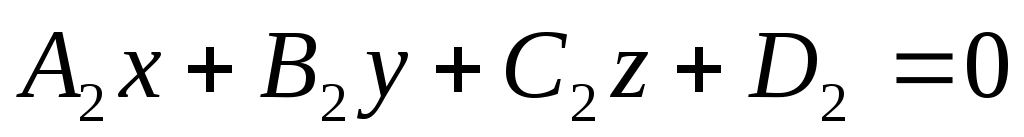
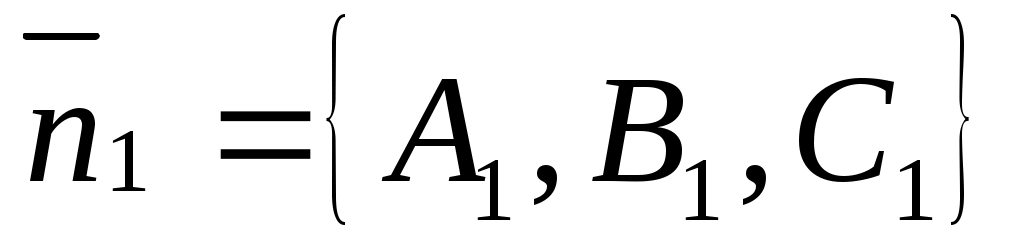 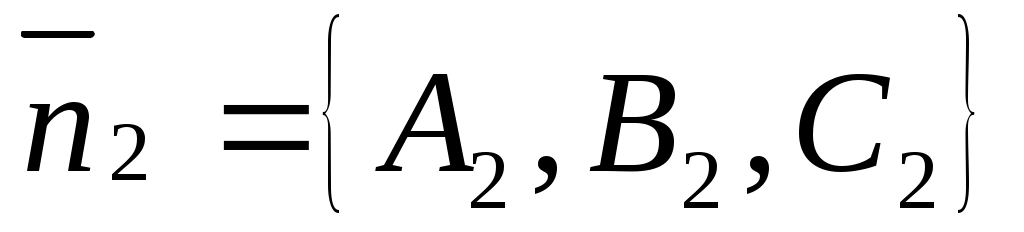
Вопрос об определении угла между плоскостями сводиться к определению угла 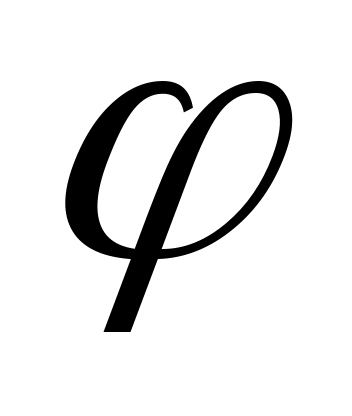 между их нормальными векторами между их нормальными векторами 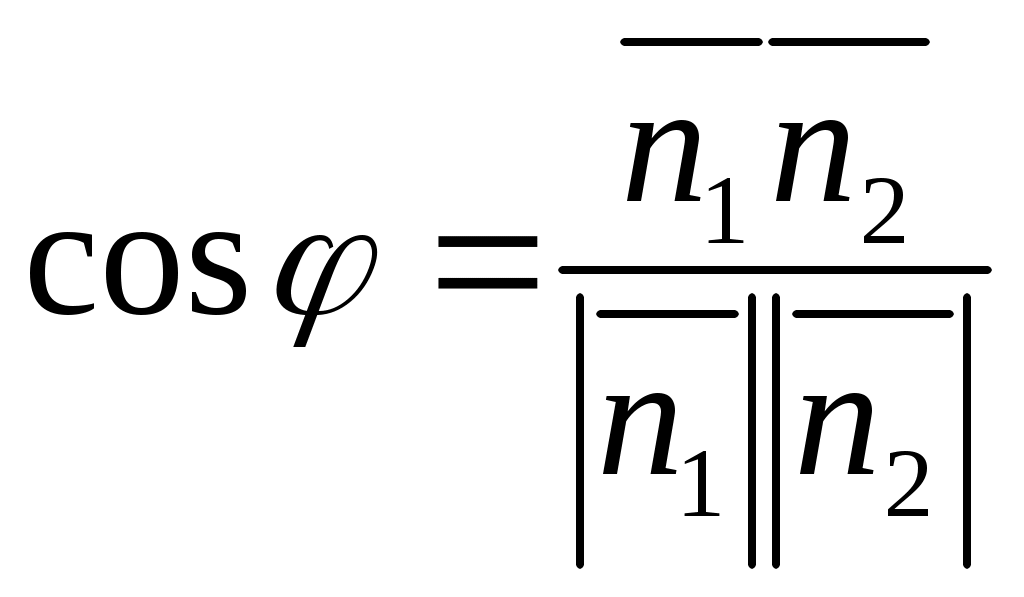
22. Условия параллельности и перпендикулярности плоскостей.
Условие параллельности: 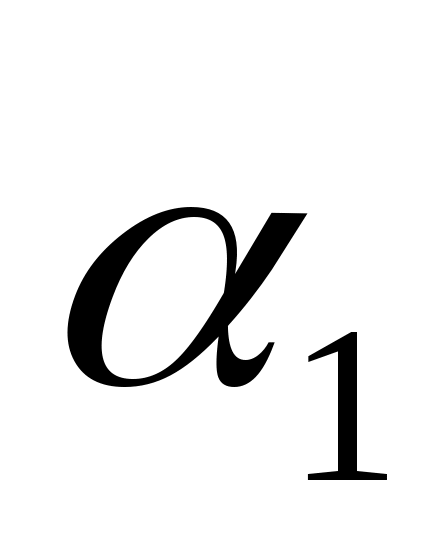 параллельна параллельна 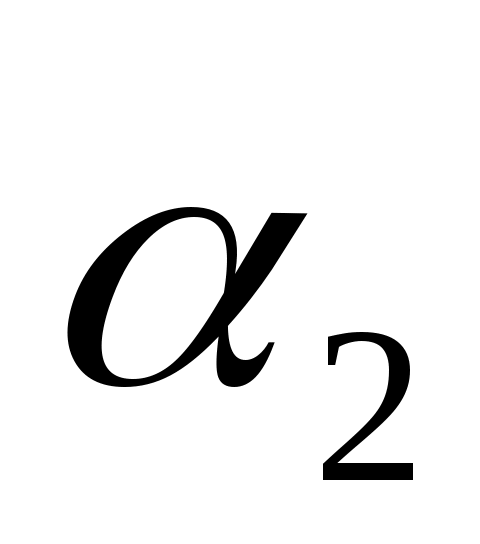 , следовательно , следовательно 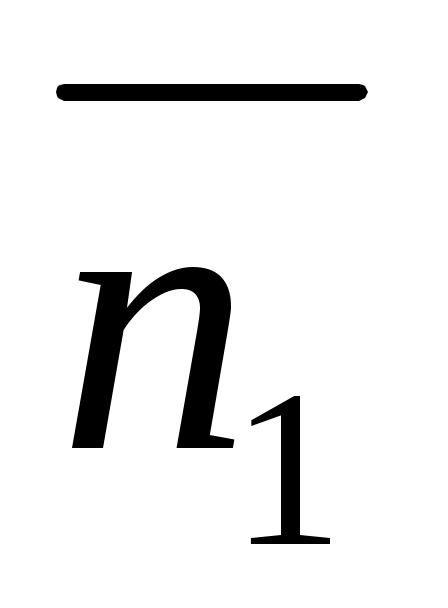 и и 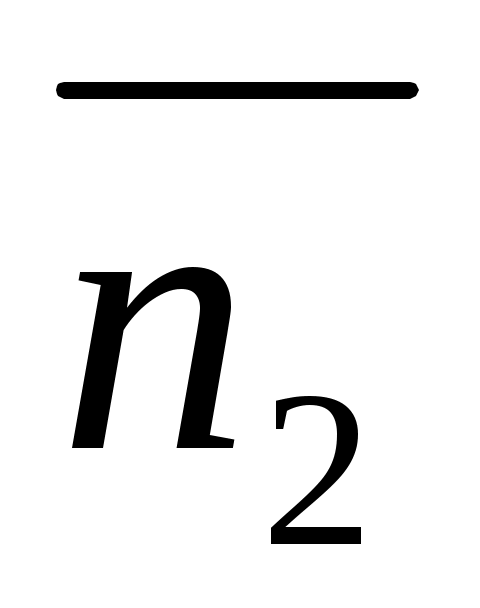 коллинеарные, следовательно коллинеарные, следовательно 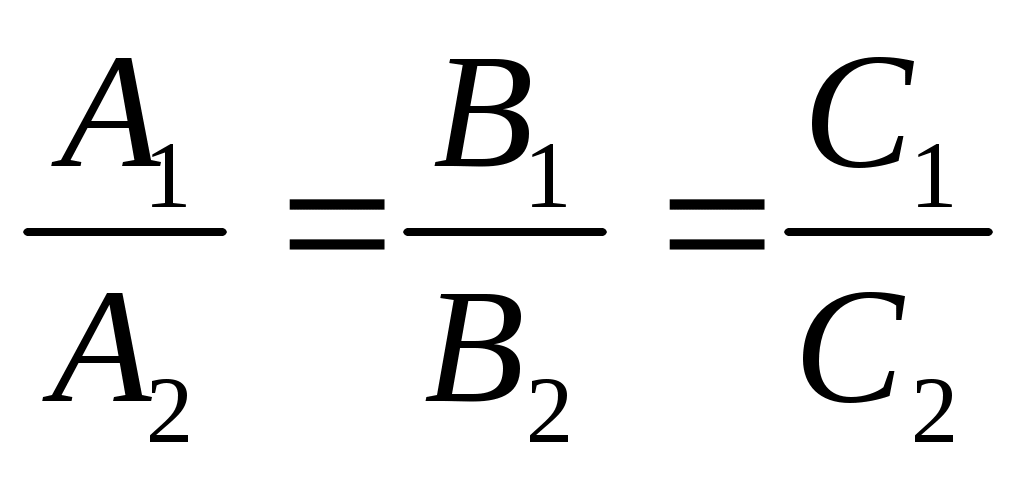
Условие перпендикулярности: 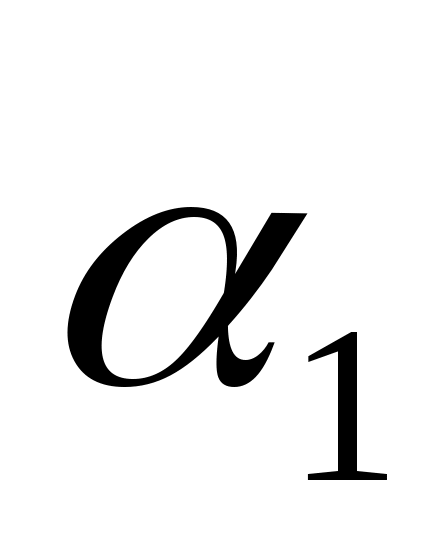 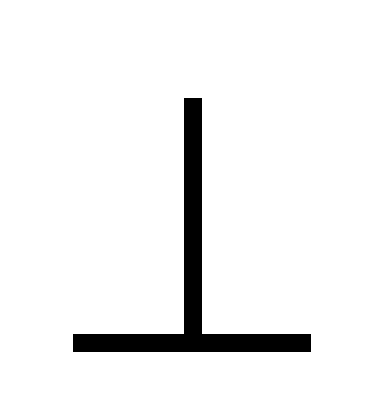 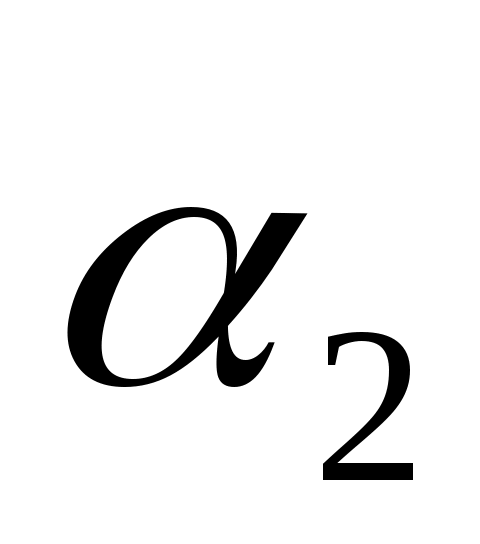 , следовательно , следовательно 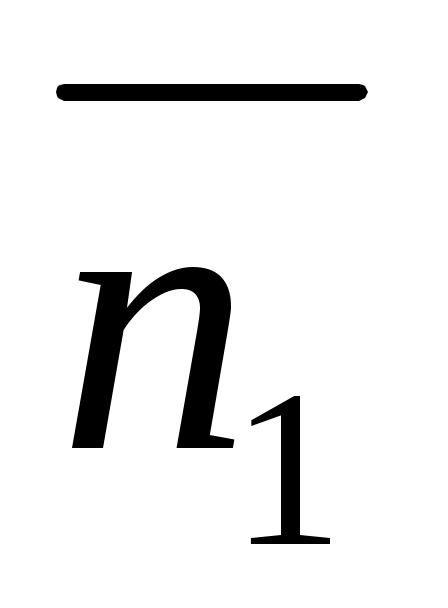 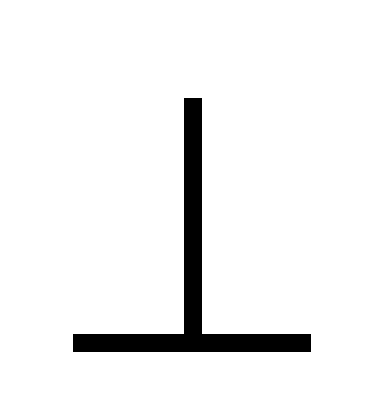 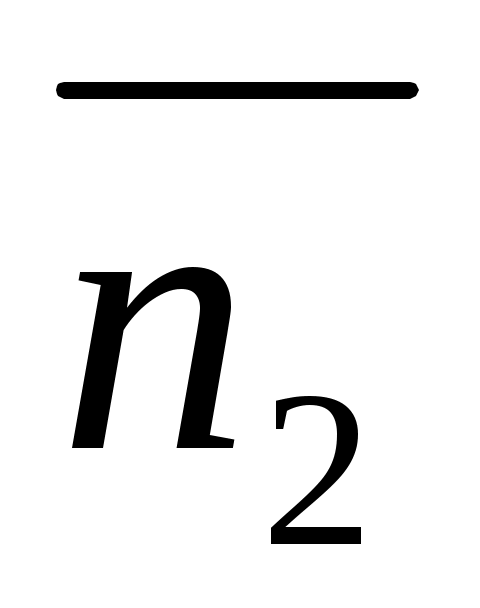
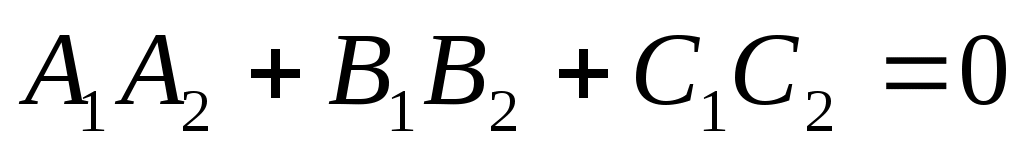
Теорема: Если два уравнения в плоскости 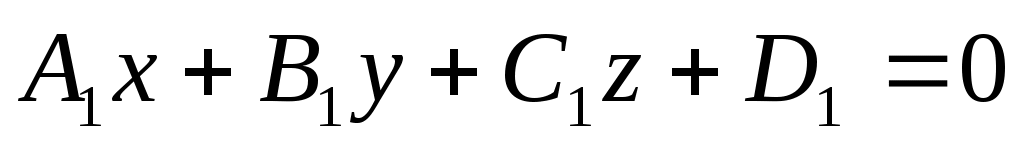 и и 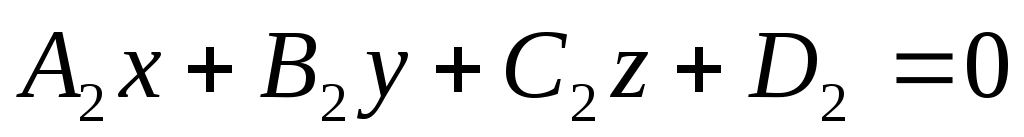
определяют одну и ту же плоскость, то их коэффициенты пропорциональны.
23. Нормированное уравнение плоскости. Расстояние от точки до плоскости.
Рассмотрим плоскость  . .
Проведем через начало координат прямую 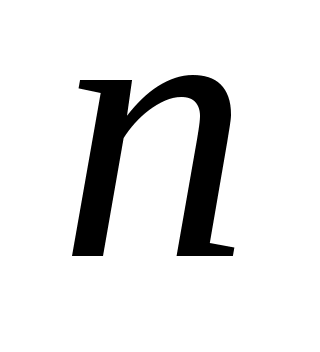 , перпендикулярно к плоскости , перпендикулярно к плоскости  . . 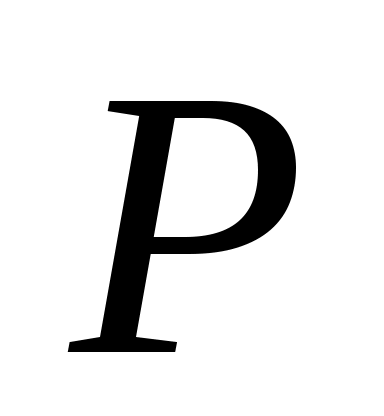 точка прямой точка прямой 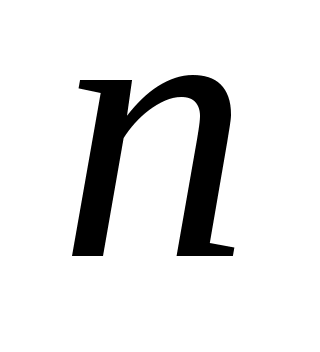 и плоскости и плоскости  . На прямой возьмем единичный вектор, направление которого совпадает с направлением . На прямой возьмем единичный вектор, направление которого совпадает с направлением  . Найти уравнение плоскости . Найти уравнение плоскости  . .
Через длину 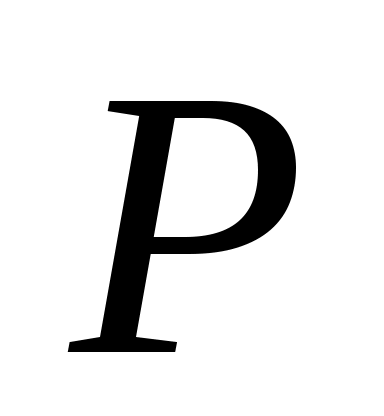 отрезка отрезка  , , 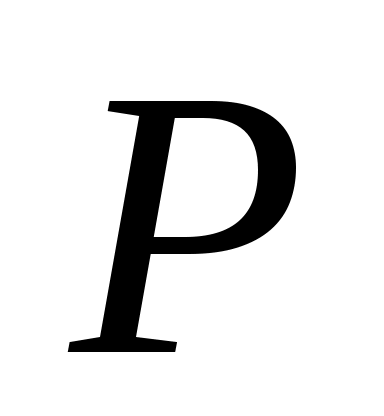 = =
Через углы наклона 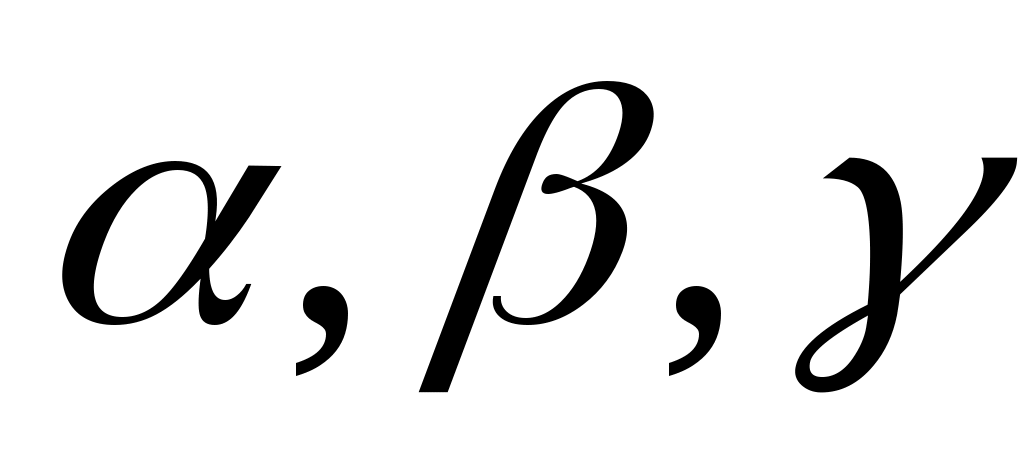 вектора вектора 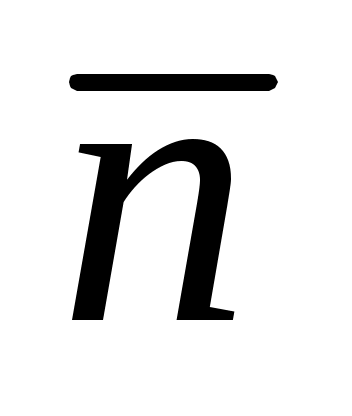 к осям к осям 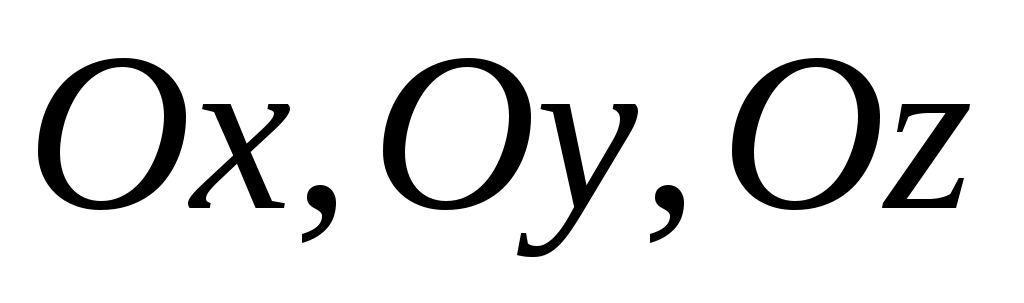 соответственно. соответственно.
Так как 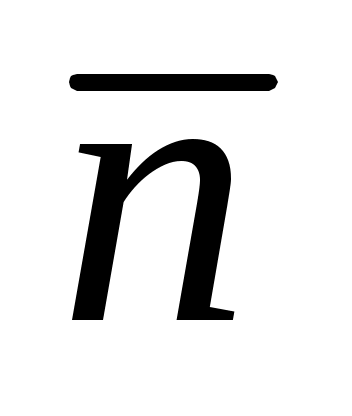 –единичный вектор, то его координаты имеют вид: –единичный вектор, то его координаты имеют вид: 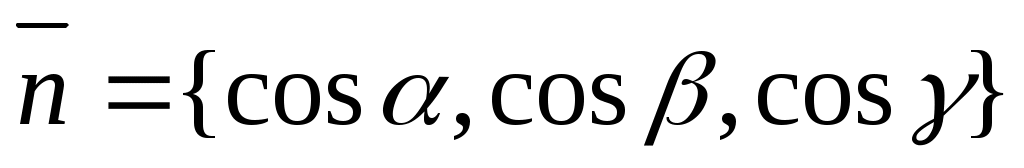
Точка 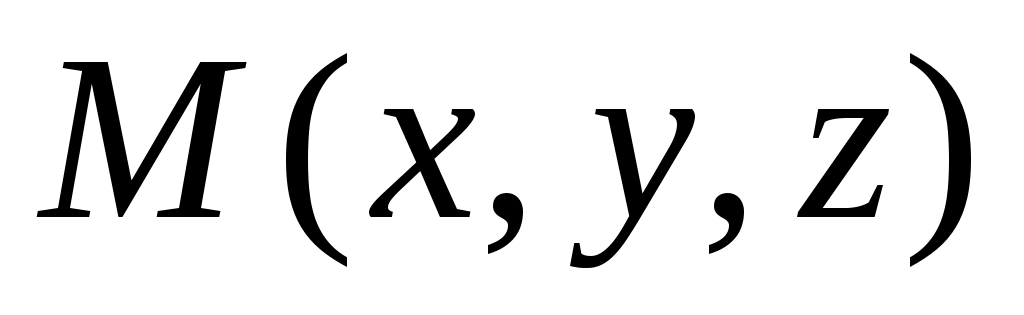 лежит на плоскости лежит на плоскости  тогда и только тогда, когда проекция вектора тогда и только тогда, когда проекция вектора  на ось, определяемую вектором на ось, определяемую вектором 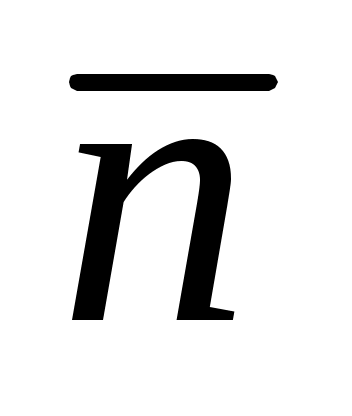 , равна , равна 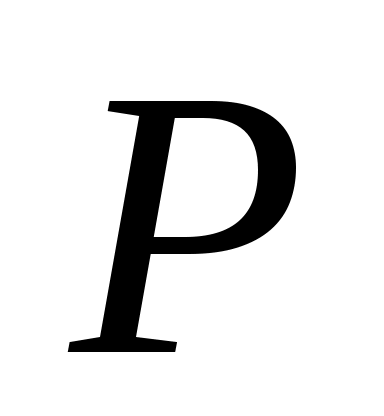 т.е при условии т.е при условии 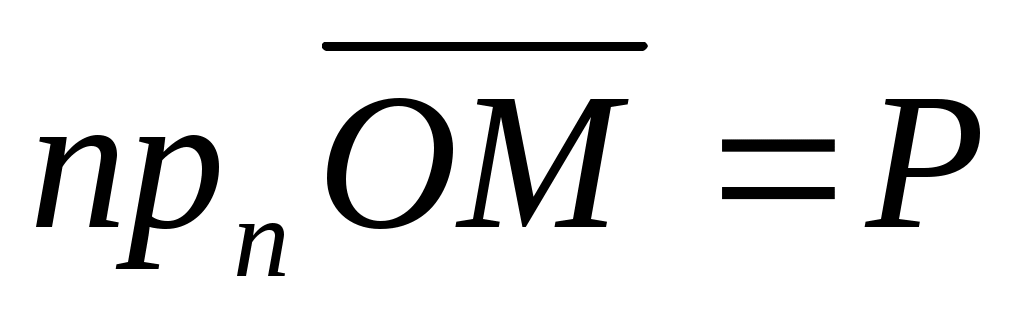
Так как 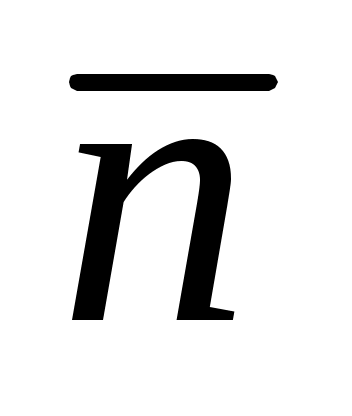 – единичный вектор – единичный вектор 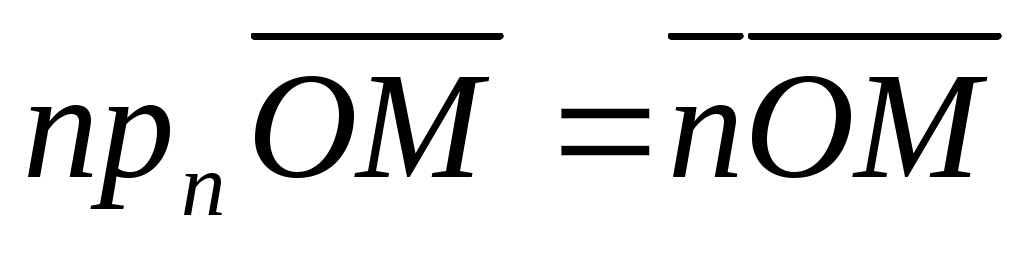 , , 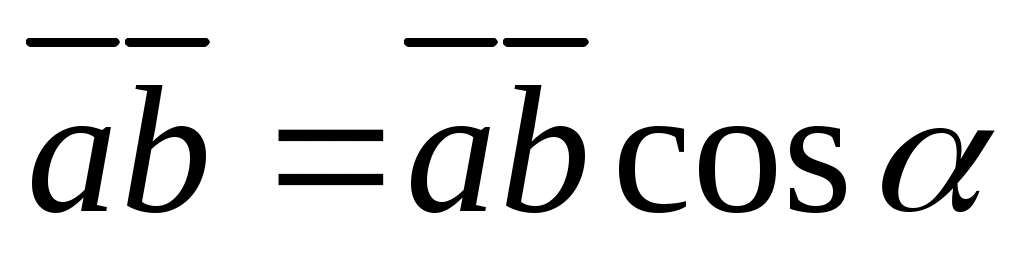 . .
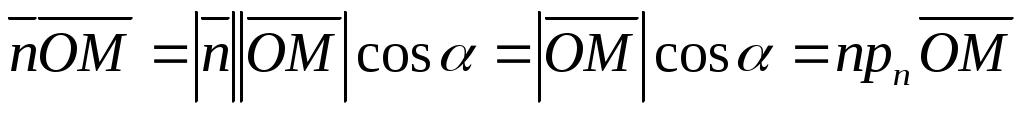 следовательно следовательно
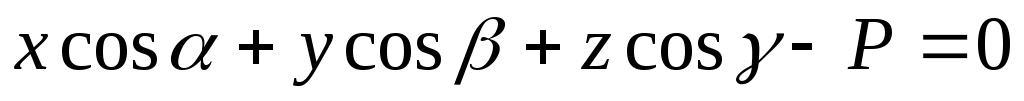 (5) нормированное уравнение плоскости. (5) нормированное уравнение плоскости.
Понятие отклонения произвольной точки  от данной плоскости от данной плоскости  . .
Пусть число 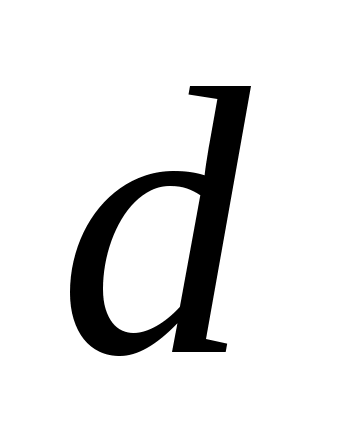 обозначает расстояние от точки обозначает расстояние от точки  до плоскости. до плоскости.
Определение: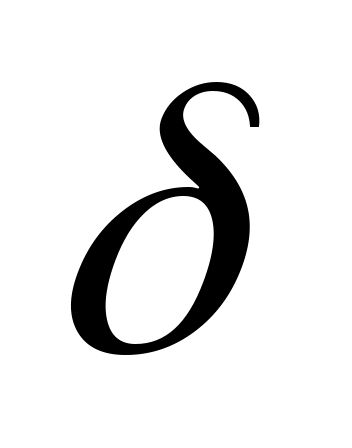 -отклонением точки -отклонением точки  от плоскости от плоскости  называется число + называется число + 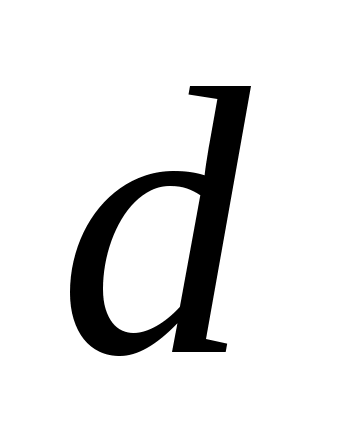 , когда точка , когда точка  и начало координат О лежат по разные стороны от плоскости и начало координат О лежат по разные стороны от плоскости  и число – и число –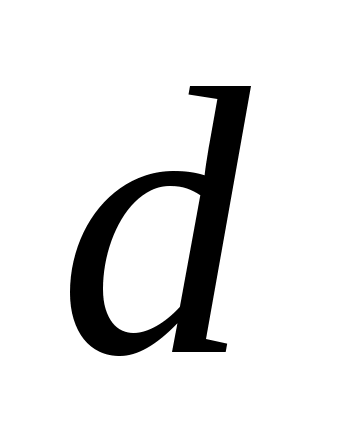 , если точки , если точки  и О лежат по одну сторону от плоскости и О лежат по одну сторону от плоскости  . .
Теорема: Левая часть нормированного уравнения плоскости (5) равна отклонению точки  с координатами с координатами 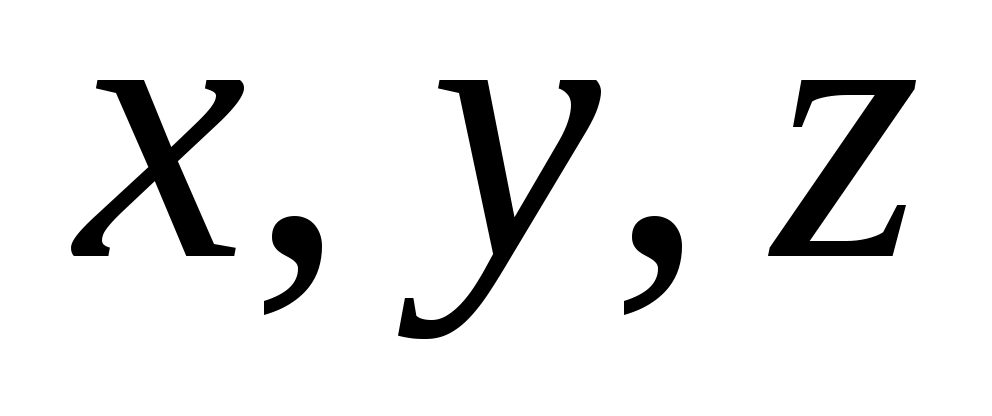 от плоскости определяемой общим уравнением плоскости (1) от плоскости определяемой общим уравнением плоскости (1)
Для нахождения отклонения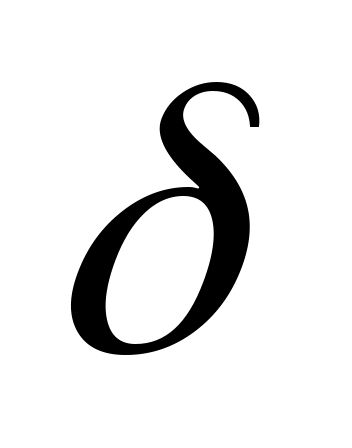 точки точки 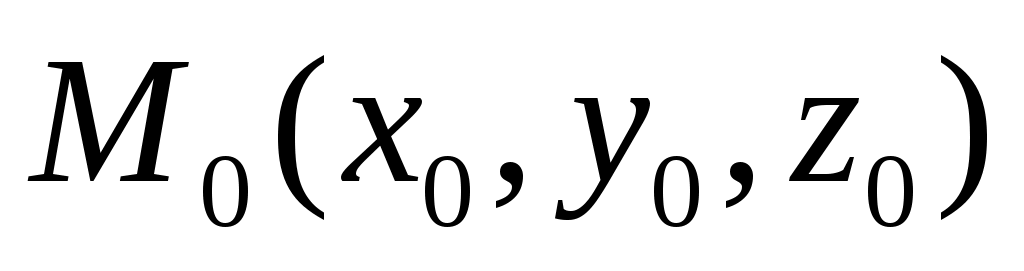 от плоскости от плоскости  следует в левую часть нормированного уравнения плоскости следует в левую часть нормированного уравнения плоскости  подставить на место подставить на место 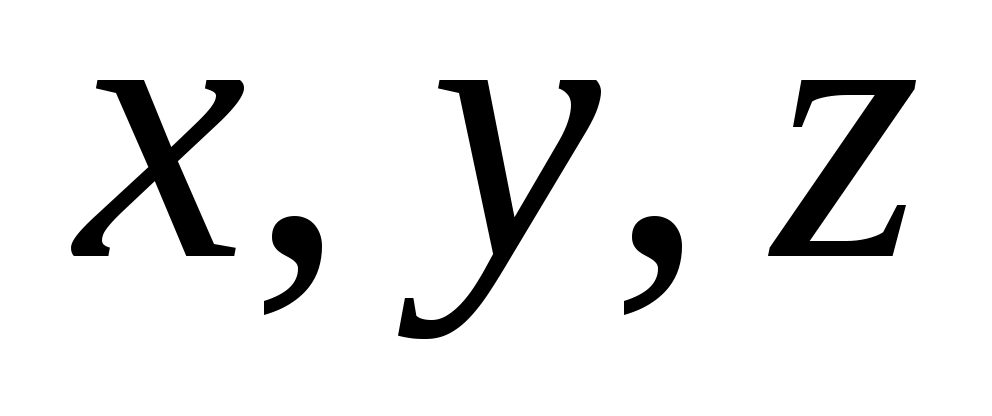 координаты точки координаты точки 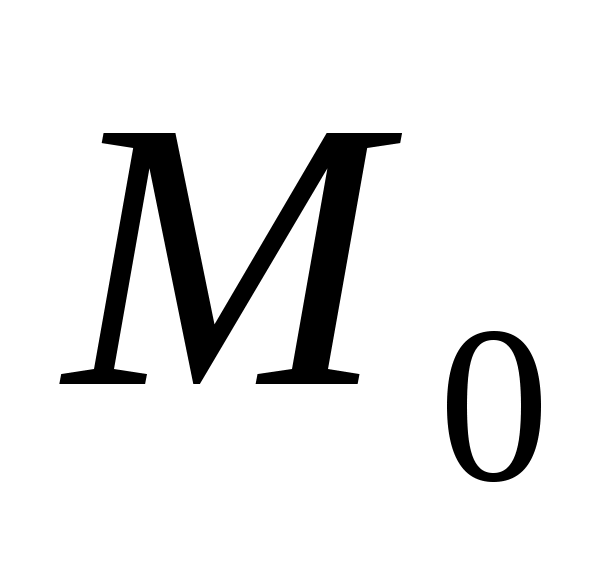 . .
Расстояние от точки  до плоскости равно модулю отклонения. до плоскости равно модулю отклонения. 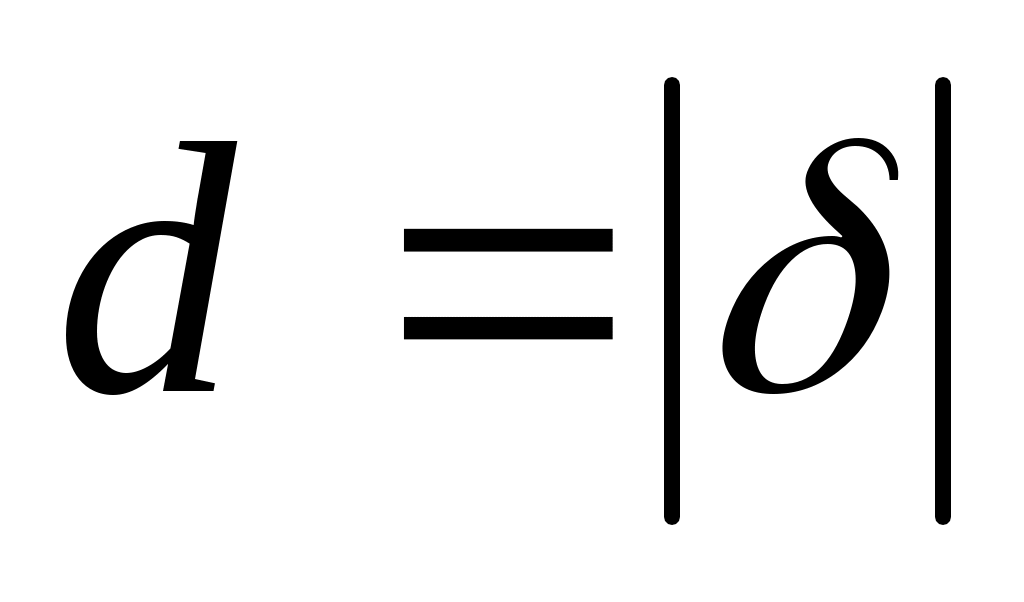
Алгоритм приведения общего уравнения плоскости к нормированному виду
Дано общее уравнение 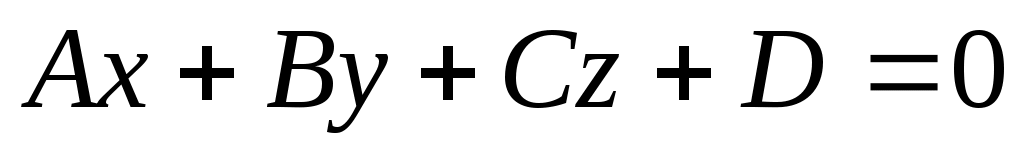 и и 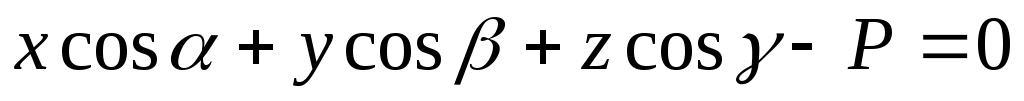
эти плоскости должны определять одну и ту же плоскость, то найдется число 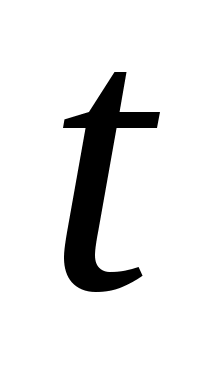 такое, что такое, что 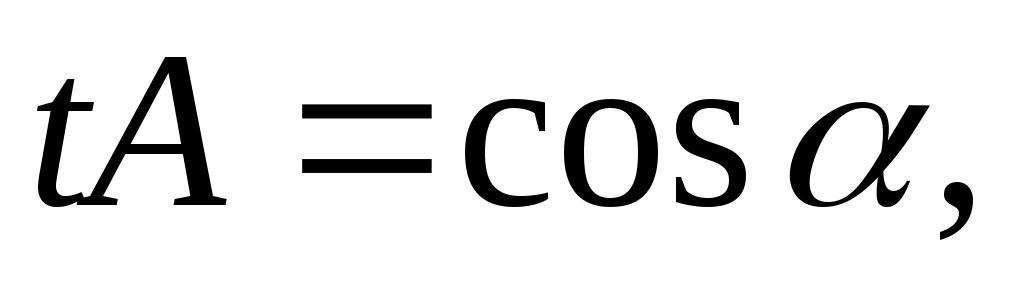 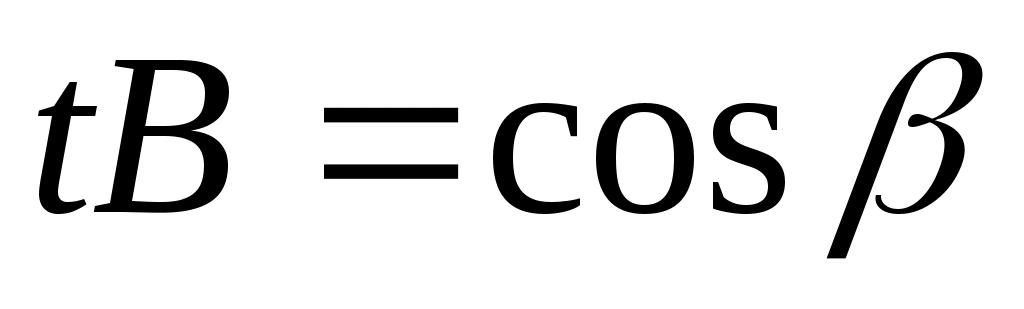 , , 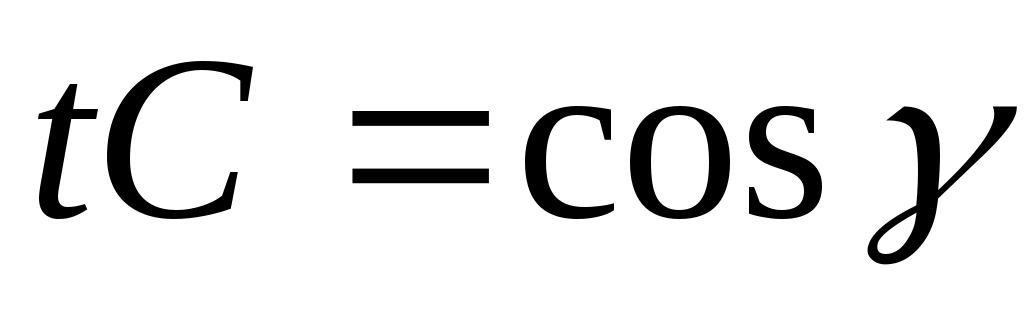 , , 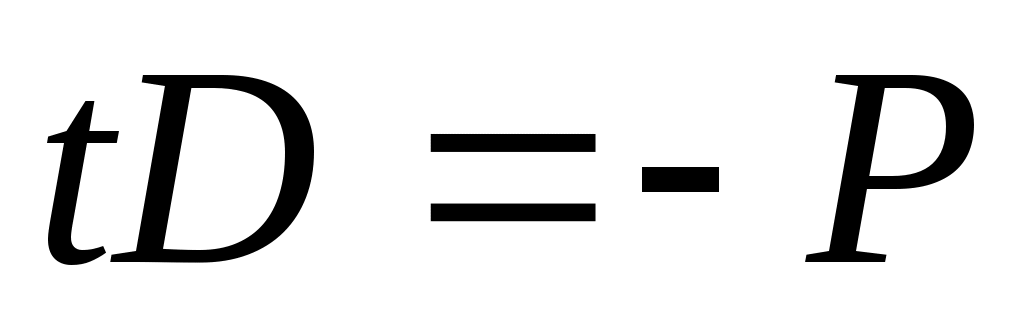
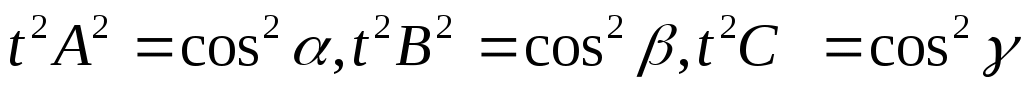
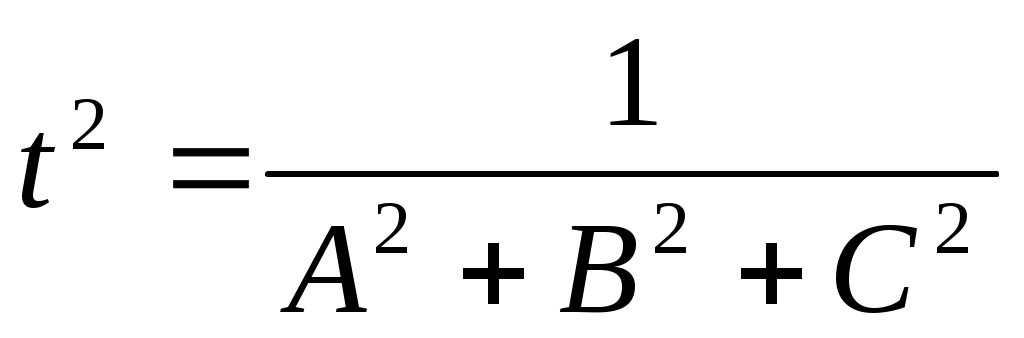 следовательно следовательно 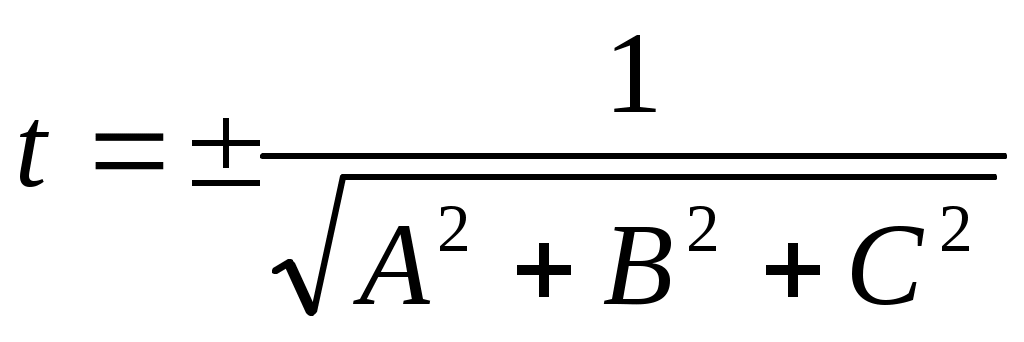
Так как по смыслу расстояние 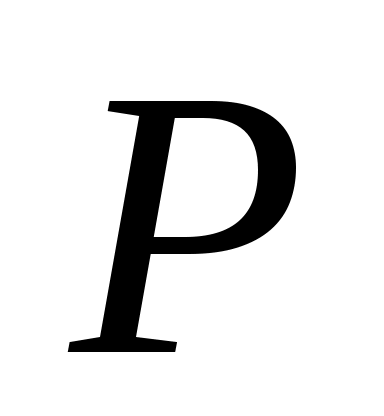 всегда неотрицательно, то из всегда неотрицательно, то из 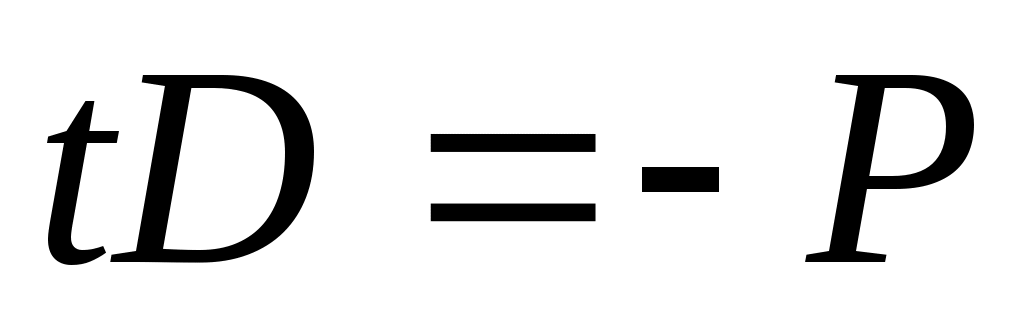 заключаем, что знак заключаем, что знак 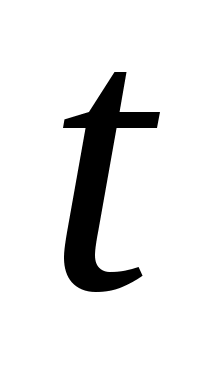 противоположен знаку противоположен знаку 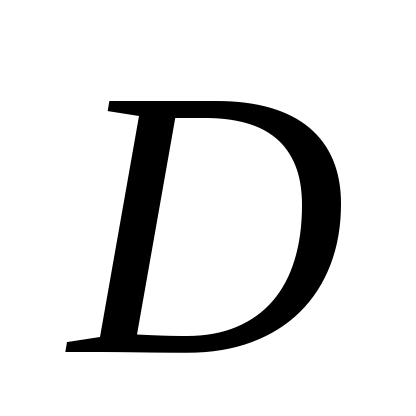 . Для приведения общего уравнения плоскости к нормированному виду, следует его умножить на нормирующий множитель, знак которого противоположен по знаку . Для приведения общего уравнения плоскости к нормированному виду, следует его умножить на нормирующий множитель, знак которого противоположен по знаку 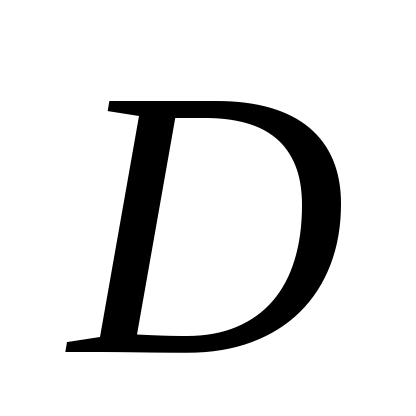
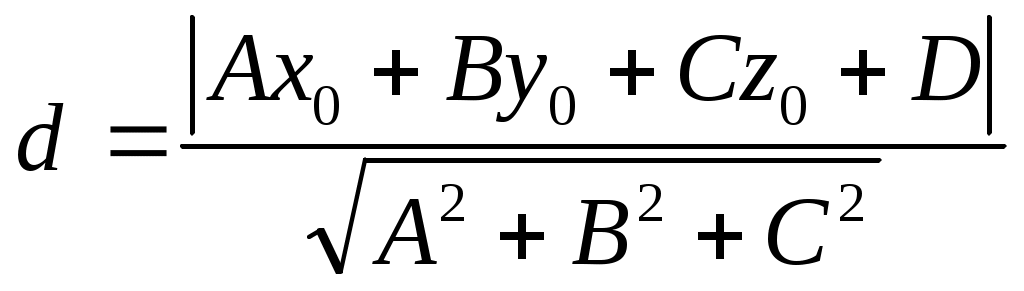 - формула для вычиления расстояния от точки до плоскости. - формула для вычиления расстояния от точки до плоскости.
24. Уравнение прямой в пространстве. Его каноническое уравнение. Параметрические уравнение прямой. Уравнение прямой проходящей через данные две точки
Канонические уравнения прямой в пространстве
Определение: Прямая линия в пространстве определяется как пересечение двух плоскостей, определяется совместным заданием двух уравнений первой степени 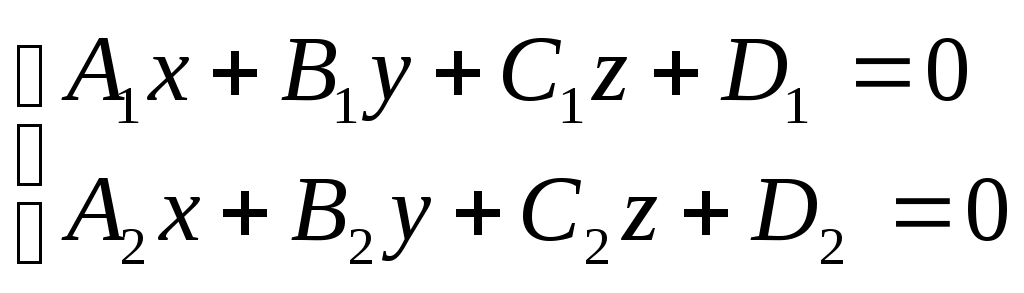 (1) при условии (1) при условии 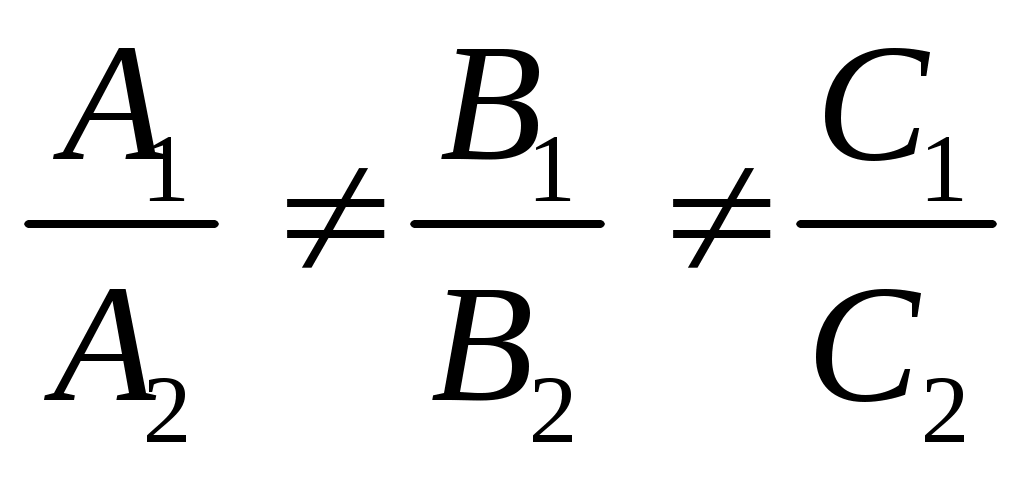
Определение: Любой не нулевой вектор параллельный данной прямой называется направляющим вектором этой прямой.
Вывод уравнения прямой, проходящей через данную точку пространства 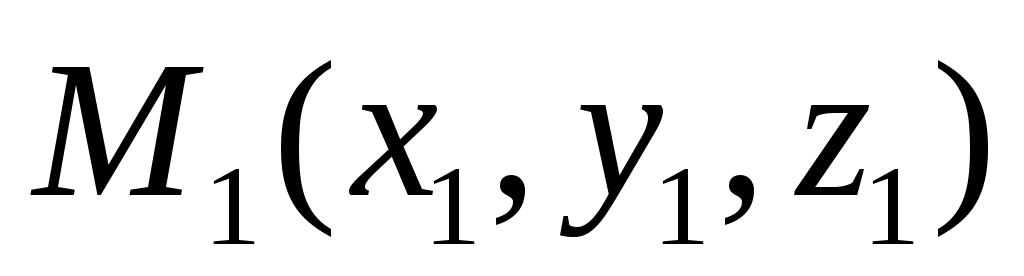 и имеющий заданный направляющий вектор и имеющий заданный направляющий вектор 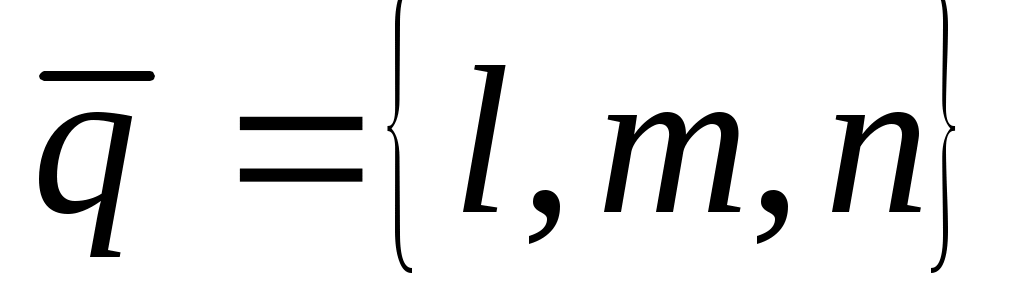 . .
Точка 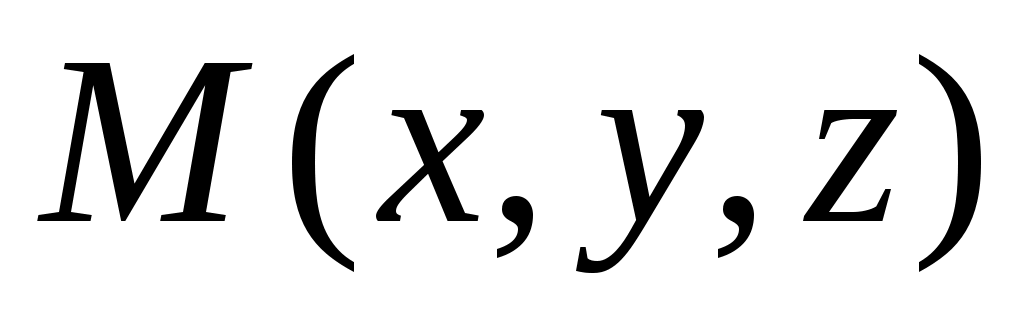 лежит на прямой тогда и только тогда, когда векторы лежит на прямой тогда и только тогда, когда векторы 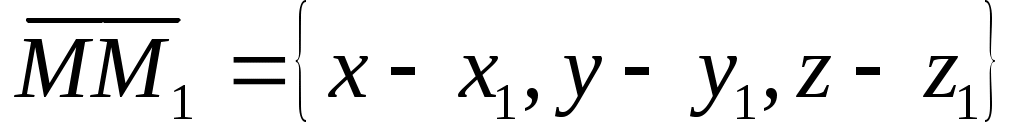 и и 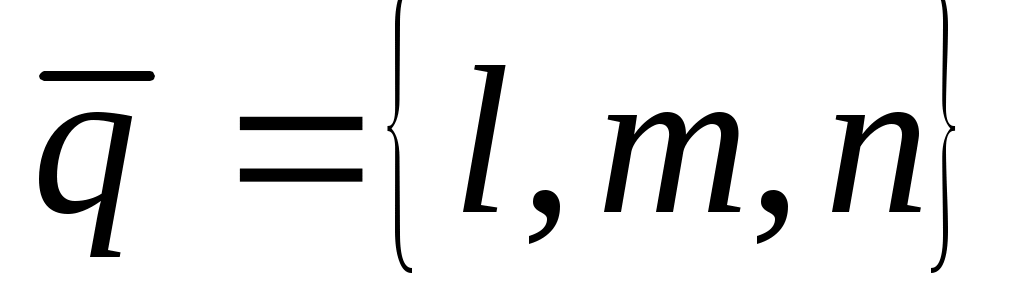 коллинеарны. коллинеарны.
Условие коллиниарности 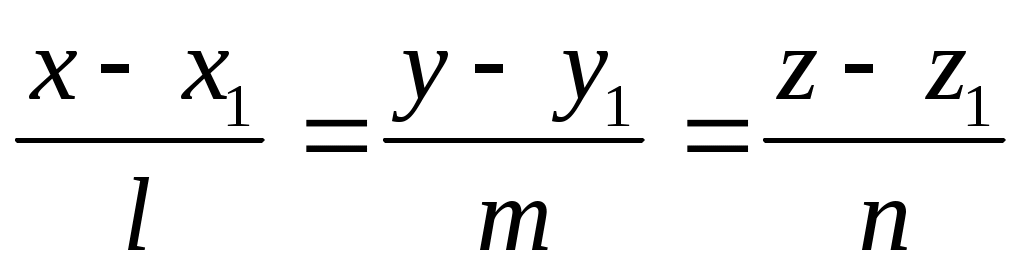 (2) (2)
Уравнения (2) называются каноническими уравнениями прямой в пространстве.
Иногда имеет случай 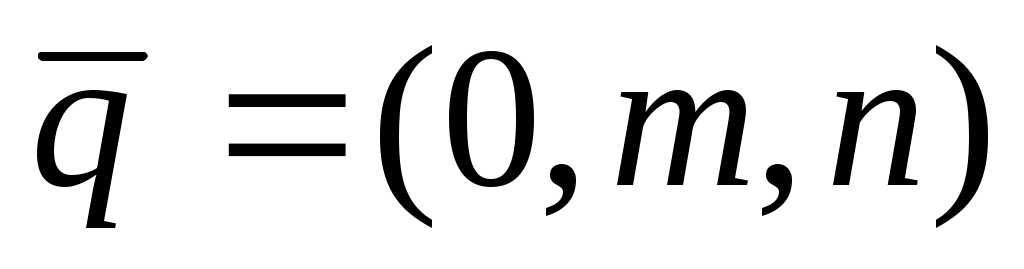  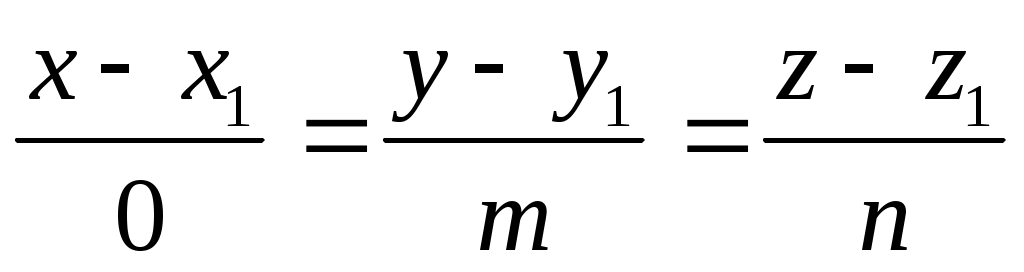
Обращение в нуль одного из знаменателей в (2) означает что обращение в нуль и соответствующего числителя.
Уравнение прямой, проходящей через две данные точки 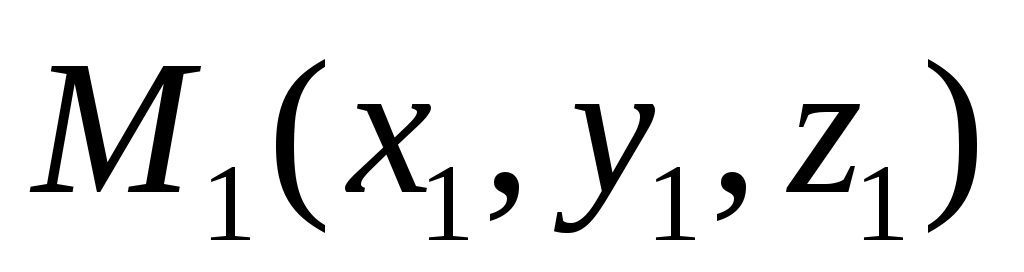 , , 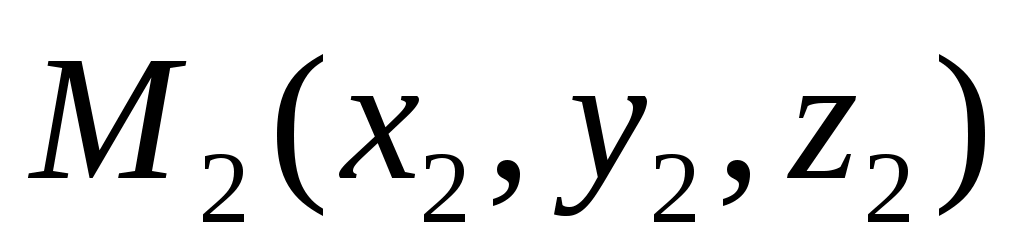
Уравнение прямой проходит через точку 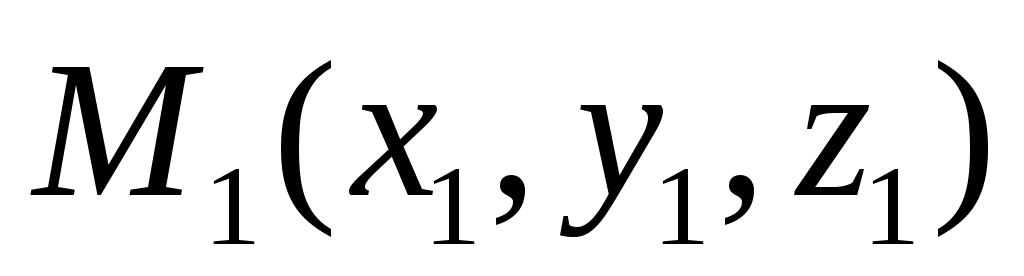 и имеет направляющий вектор и имеет направляющий вектор 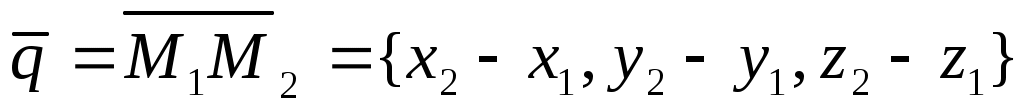 . .
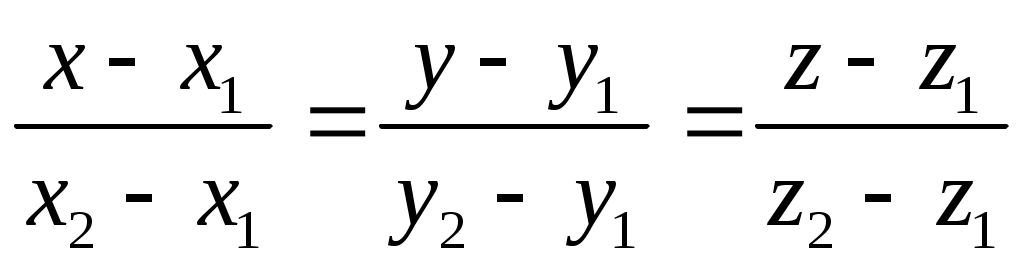 (3) - уравнение прямой, проходящей через две данные точки (3) - уравнение прямой, проходящей через две данные точки 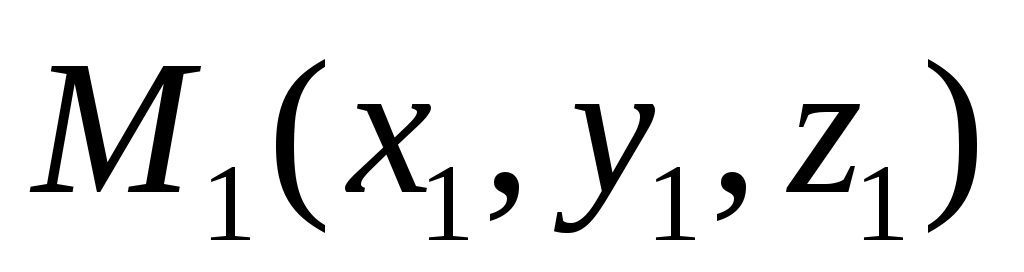 , , 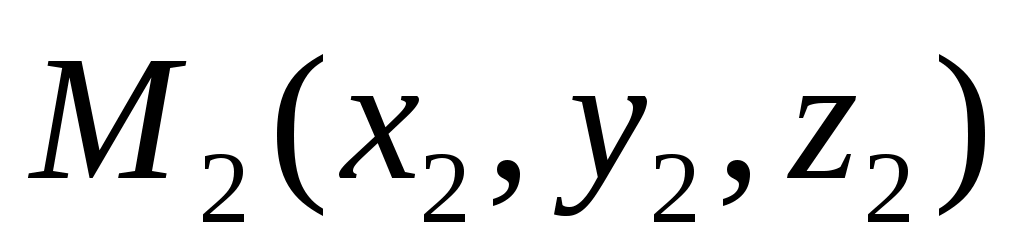
Параметрические уравнения прямой получаются из канонических уравнений прямой.
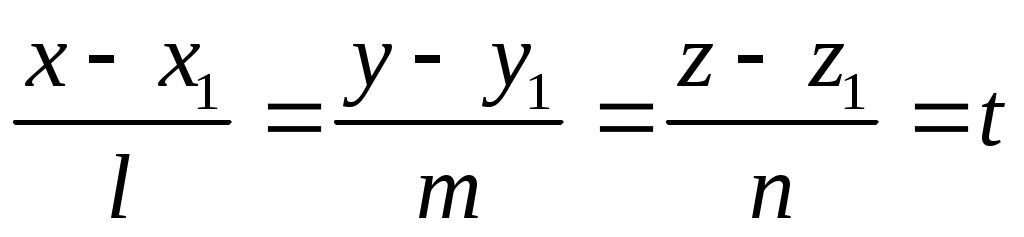 , где , где 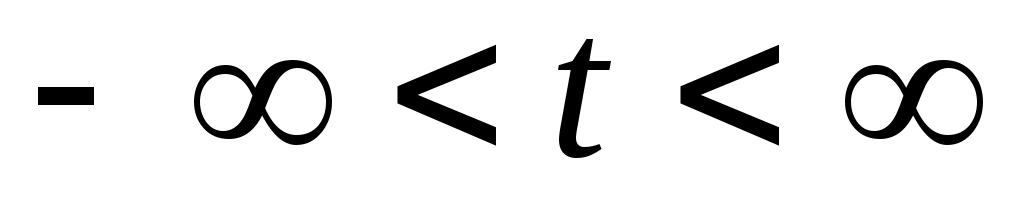 . .
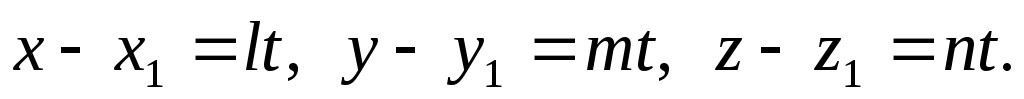
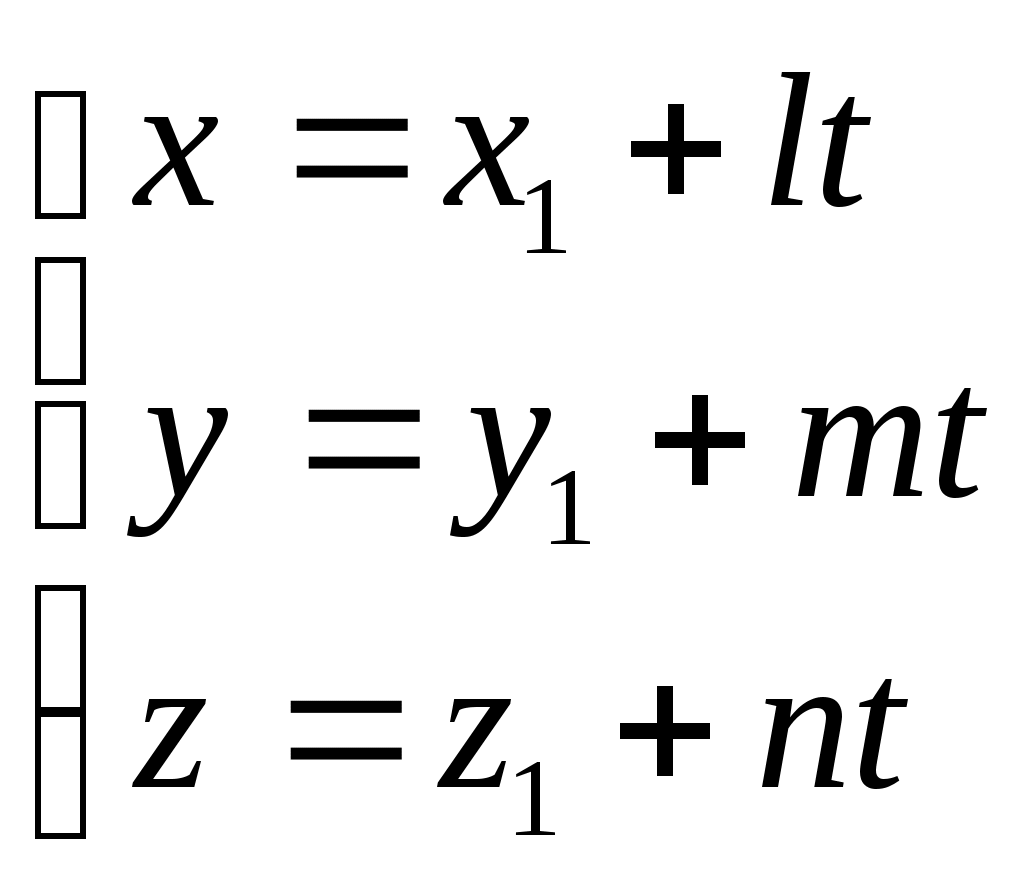 (4) – параметрические уравнения прямой. (4) – параметрические уравнения прямой.
25. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых в пространстве.
Пусть прямые 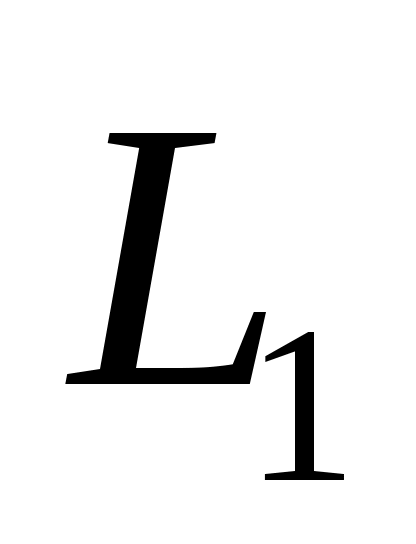 и и 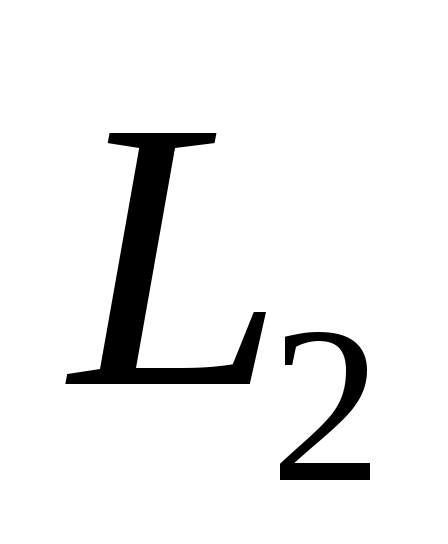 заданы своими каноническими уравнениями. заданы своими каноническими уравнениями.
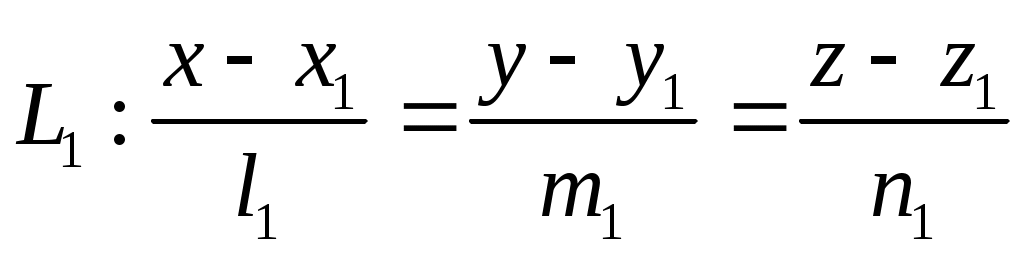
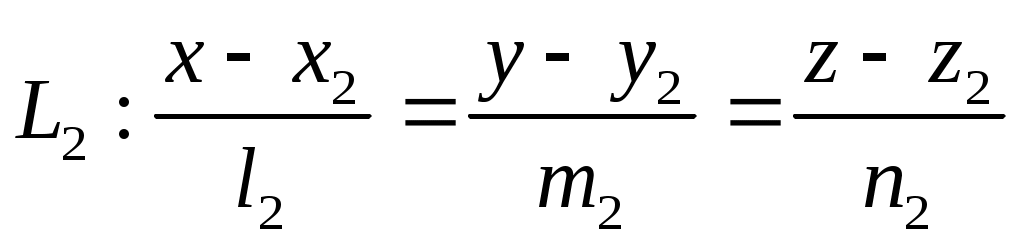 . .
Тогда задача определение угла между прямыми 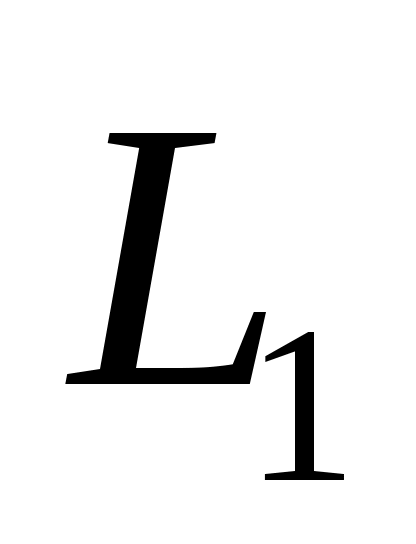 и и 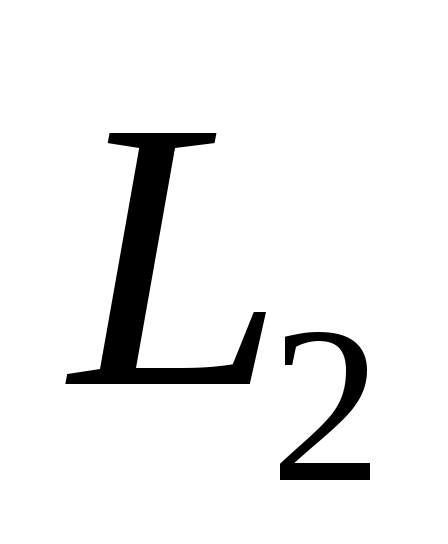 сводится к определению угла сводится к определению угла 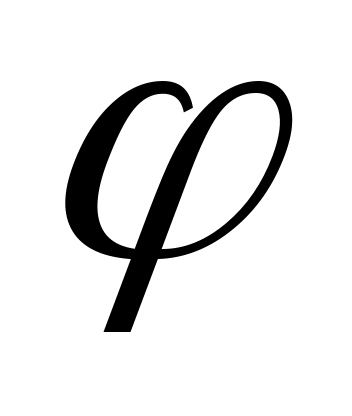 между их направляющими векторами: между их направляющими векторами: 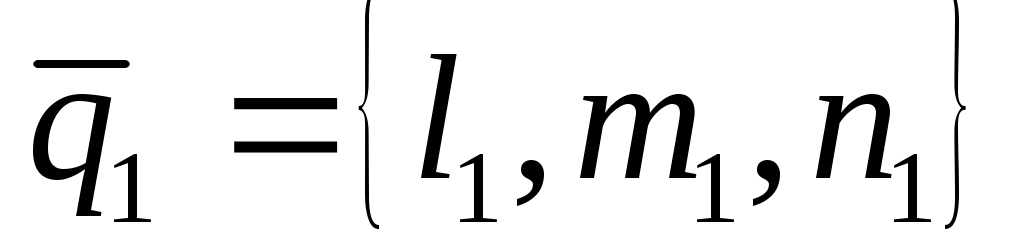 , , 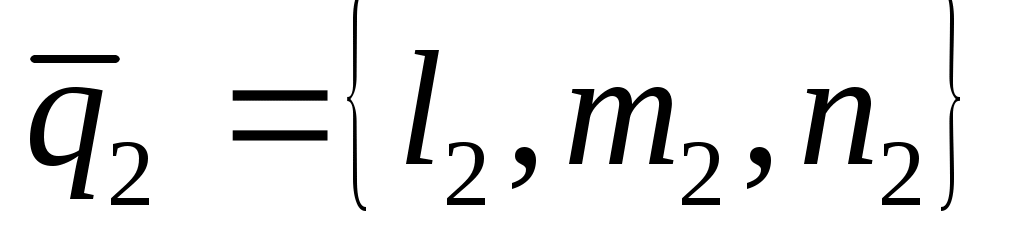
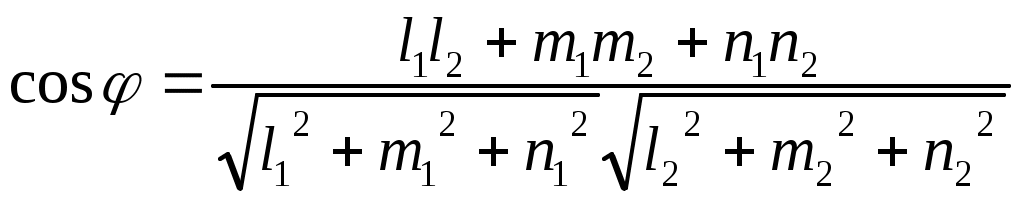 (5) –формула для определения угла между двумя прямыми. (5) –формула для определения угла между двумя прямыми.
Условие параллельности прямых 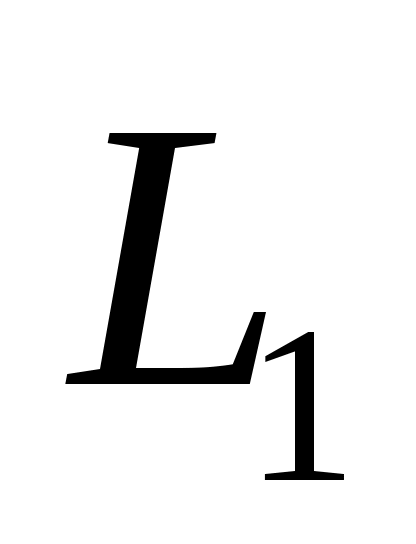 и и 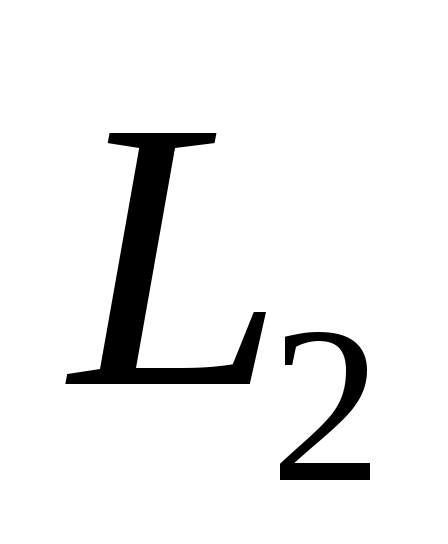 - - 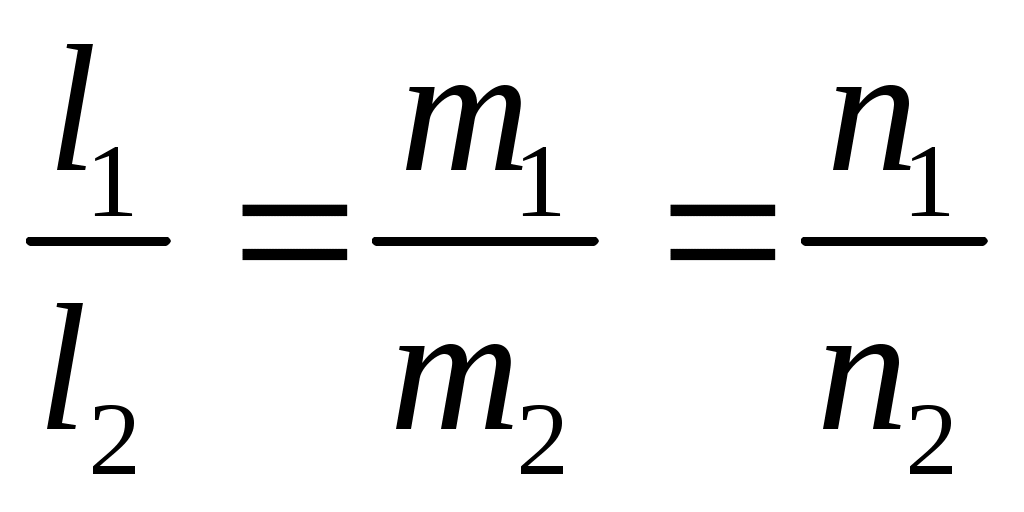 (6). (6).
Условие перпендикулярности прямых 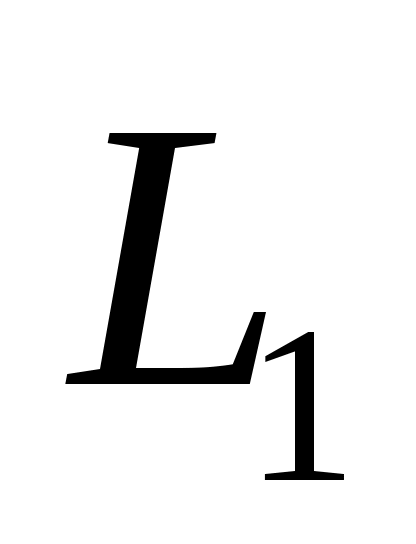 и и 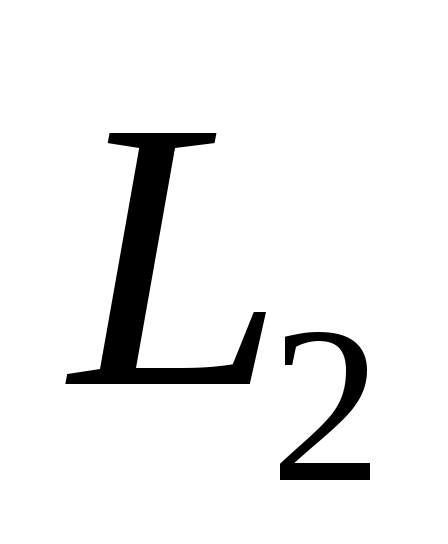 - - 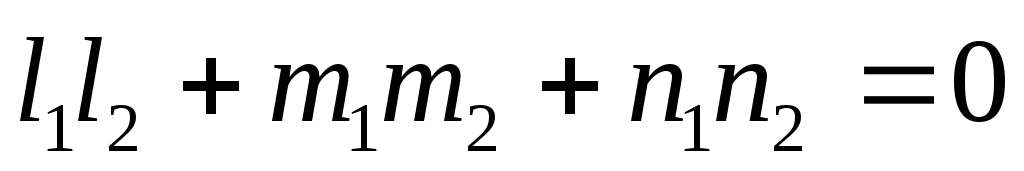 (7). (7).
26. Угол между прямой и плоскостью.
Условия параллельности и перпендикулярности прямой к плоскости
Рассмотрим плоскость , заданную общим уравнением 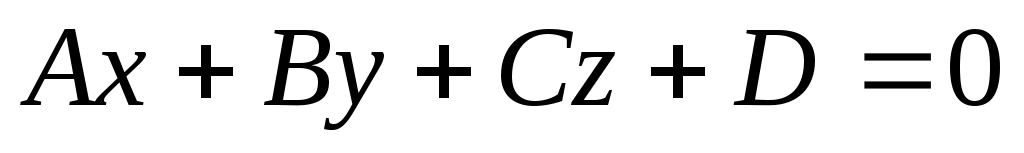 и прямую и прямую 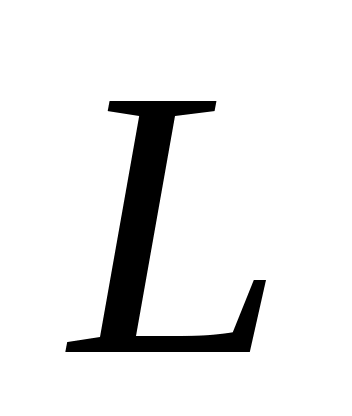 , заданную каноническими уравнениями , заданную каноническими уравнениями 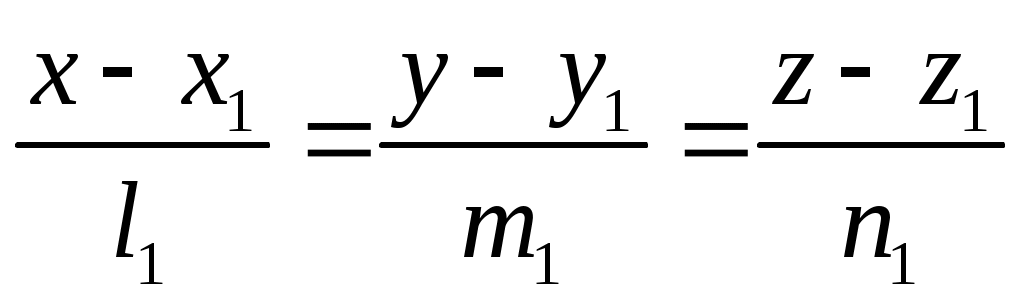
У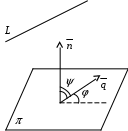 гол гол 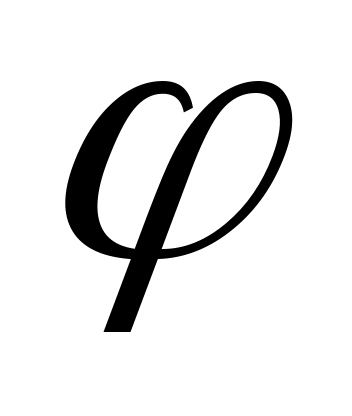 между прямой и плоскостью является дополнительным к углу между прямой и плоскостью является дополнительным к углу 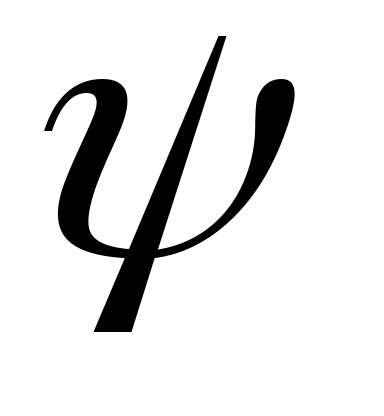 между векторами между векторами 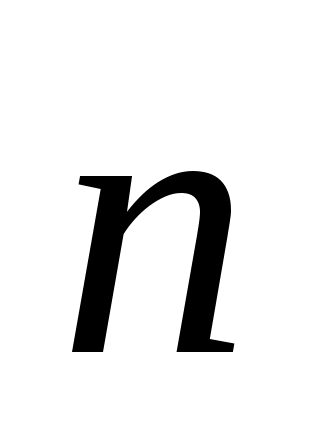 и и 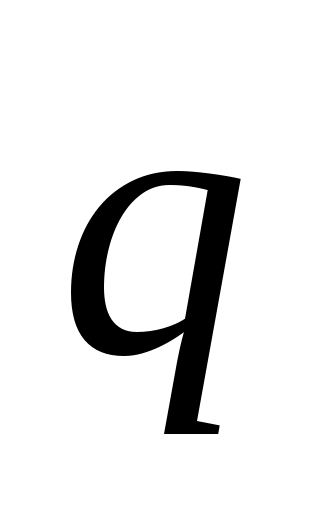
Через скалярное произведение векторов находим:
,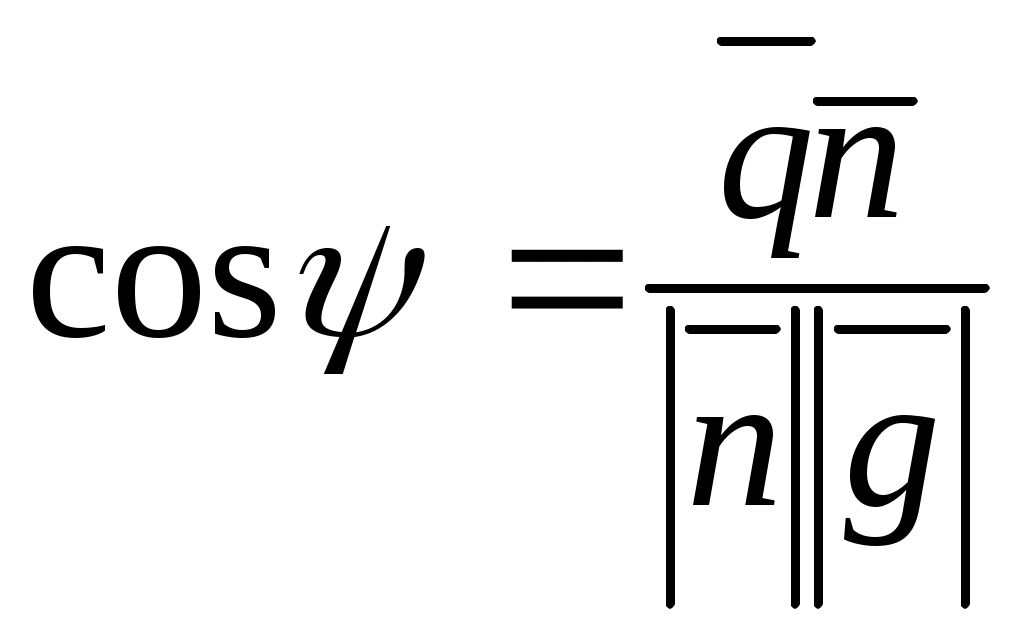 , ,
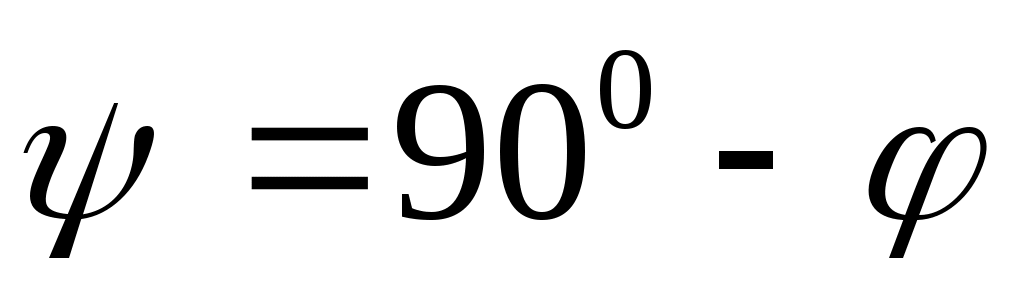
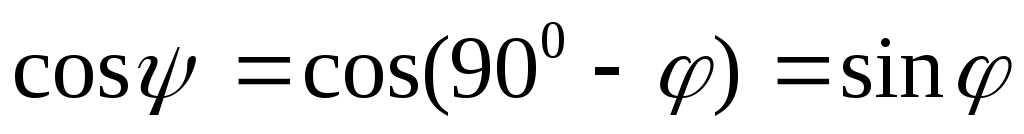 , ,
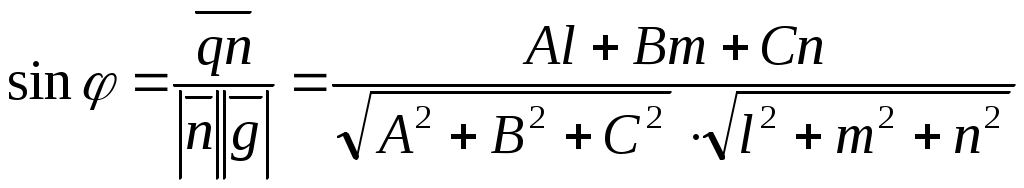 (9) - формула для определения угла между прямой и плоскостью. (9) - формула для определения угла между прямой и плоскостью.
Условие параллельности прямой 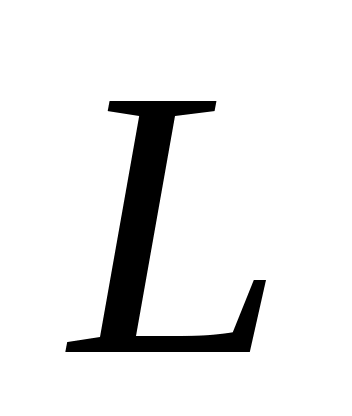 и плоскости . и плоскости .
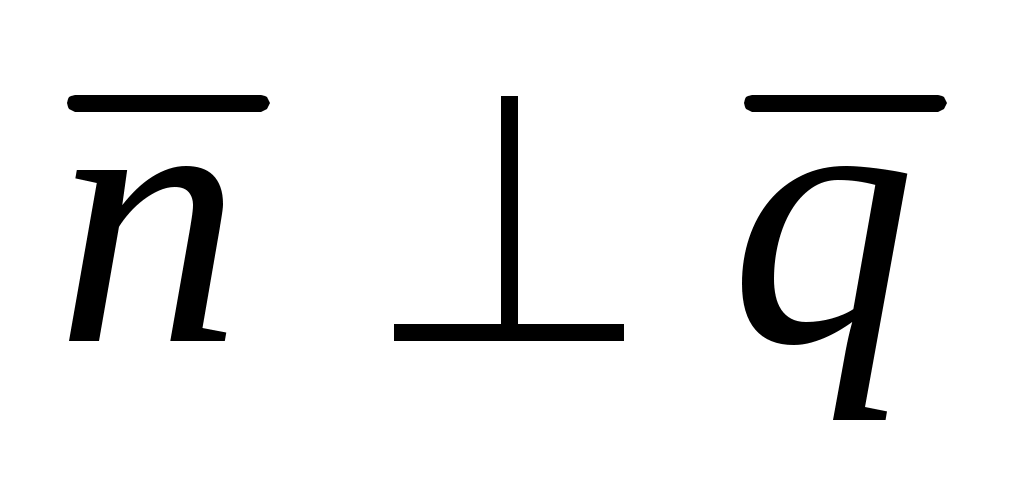 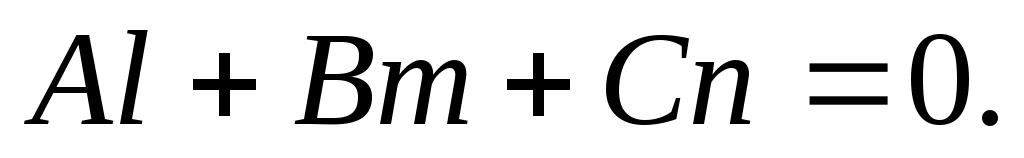
Условие перпендикулярности прямой 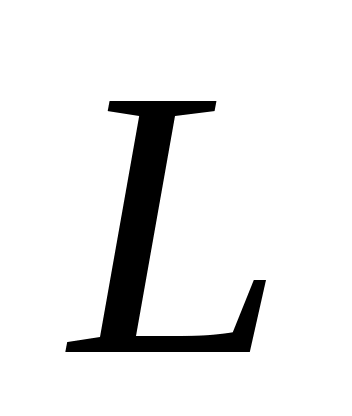 и плоскости . и плоскости .
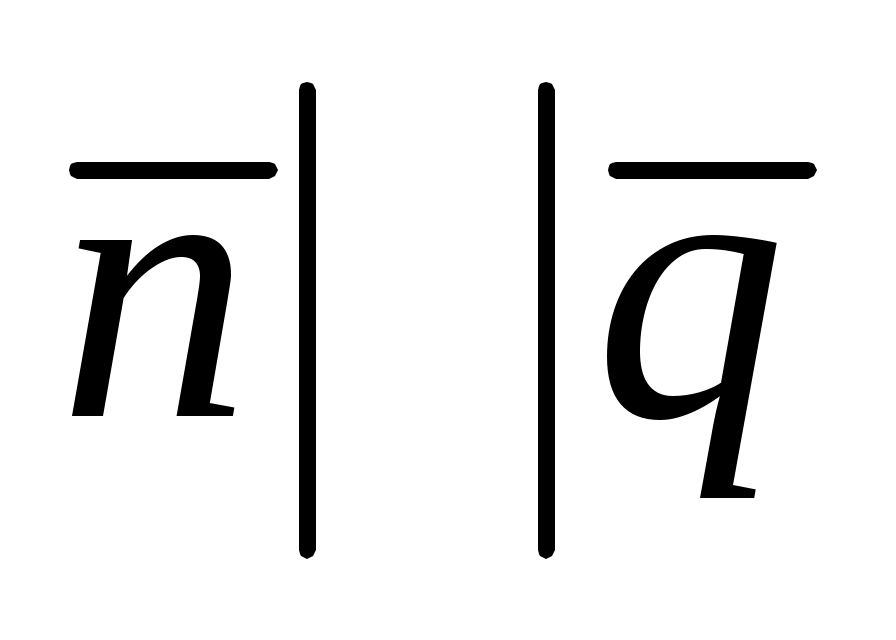 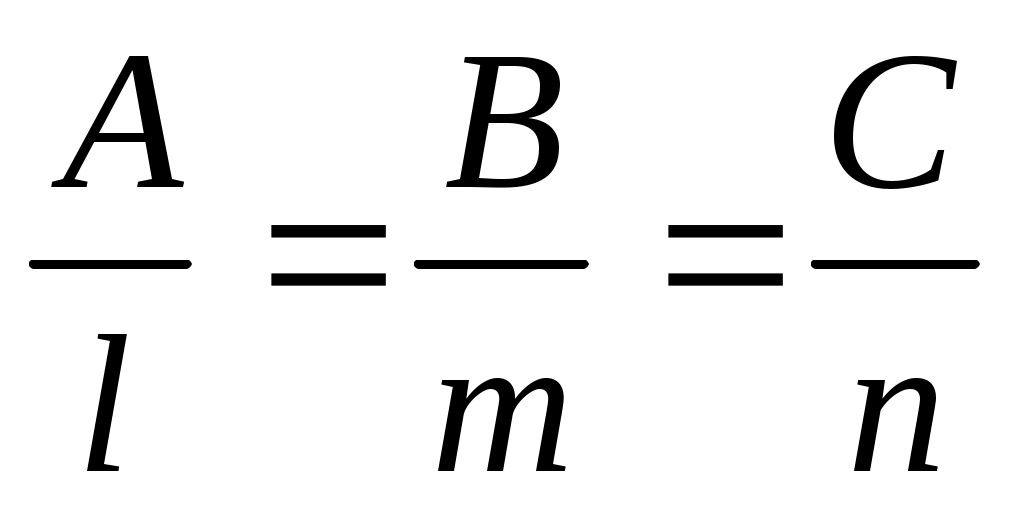 . .
27. Каноническое уравнение эллипса. Директриса и эксцентриситет эллипса.
Уравнение эллипса, свойства
Определение: Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.
F1, F2 – фокусы, точка М – произвольная точка эллипса.
F1M, F2M – фокальные радиусы эллипса.
По определению F1M+ F2M = 2a.
F2F1 = 2cрасстояние между фокусами. По определению эллипса 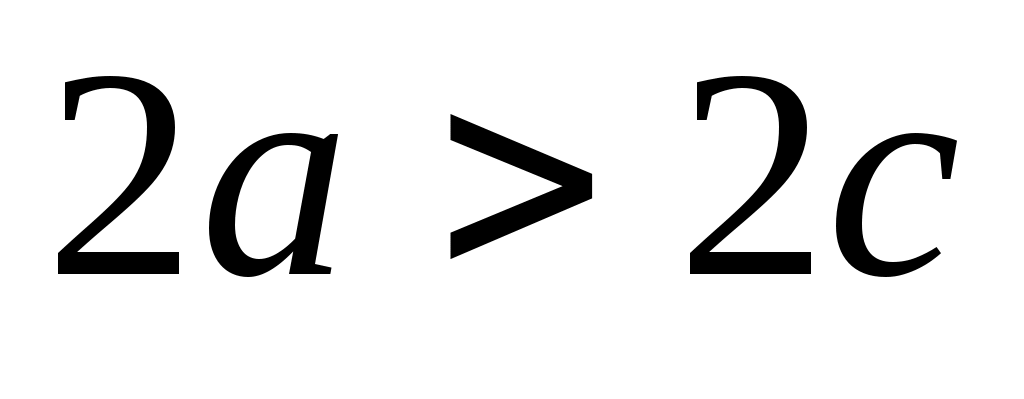 или или 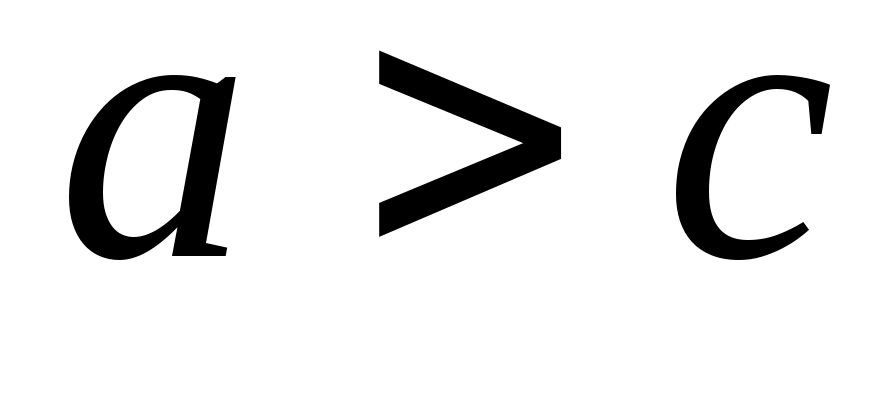 . .
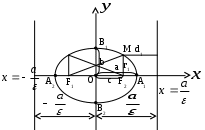
F2(-c; 0), F1(c; 0) - координаты фокусов.
Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно заданной системы координат, то в этой системе координат уравнение эллипса имеет вид:
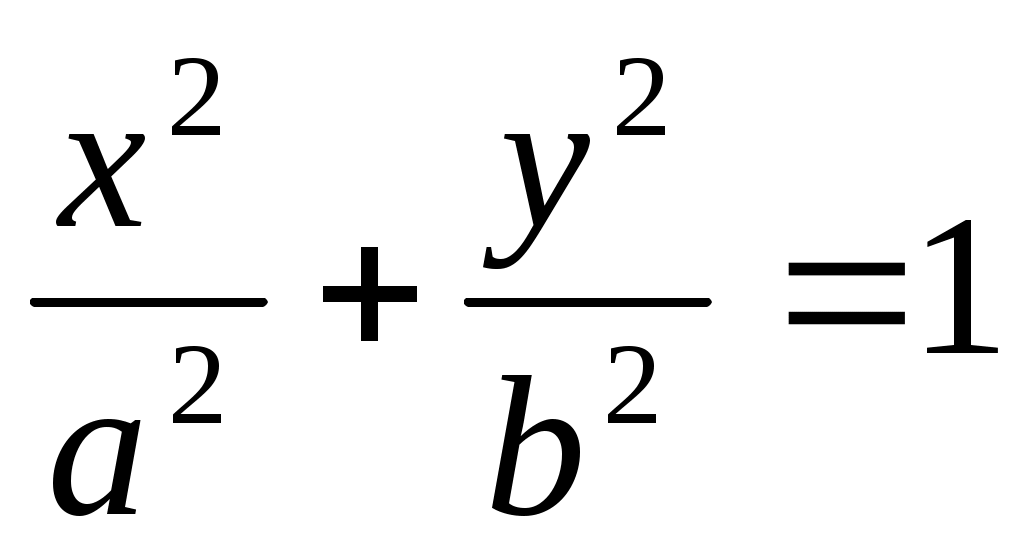 (1) – каноническое уравнение эллипса (1) – каноническое уравнение эллипса
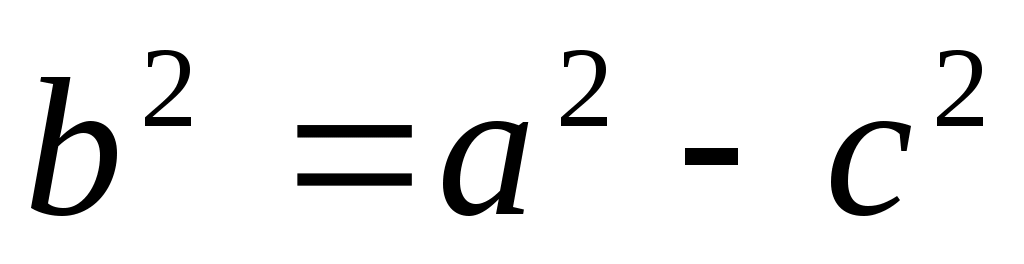 ; очевидно ; очевидно 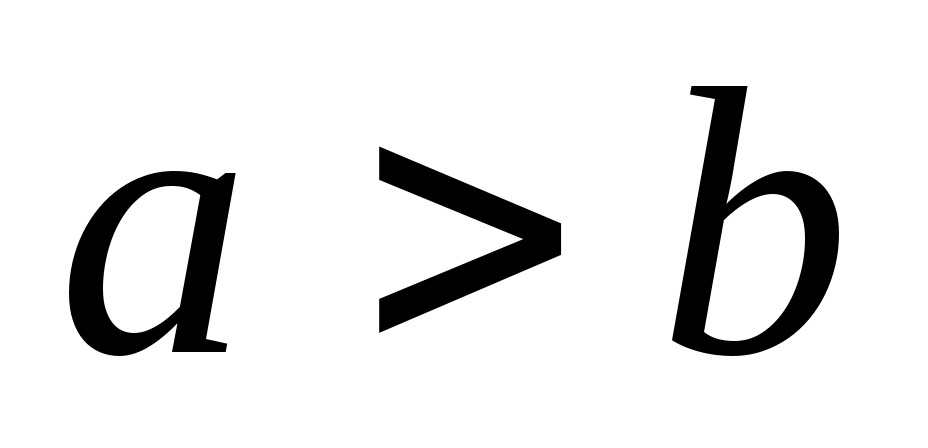 . .
|
 Скачать 1.74 Mb.
Скачать 1.74 Mb.