билеты геометрия. Билеты аналитическая геометрия. 1. Декартовы координаты на прямой
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
Свойства параболы1.Парабола имеет ось симметрии (OX). Точка пересечения параболы с осью называется вершиной параболы. 2. Вся парабола располагается в правой полуплоскости OXY. R=d 3.Директриса параболы, определяемая уравнением К 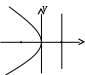 анонические уравнения: анонические уравнения: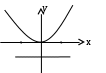 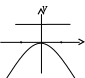 4 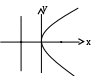 .Фокус r произвольной точки M(x;y) .Фокус r произвольной точки M(x;y) r = x+ Общее определение. Коническое сечение (эллипс, гипербола, парабола) есть геометрическое место точек, отношение расстояний которых до данной точки (F) и до данной прямой (директрисы) есть постоянная величина - 30. Эллипсоид Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением Уравнение (1) называется каноническим уравнением эллипсоида. 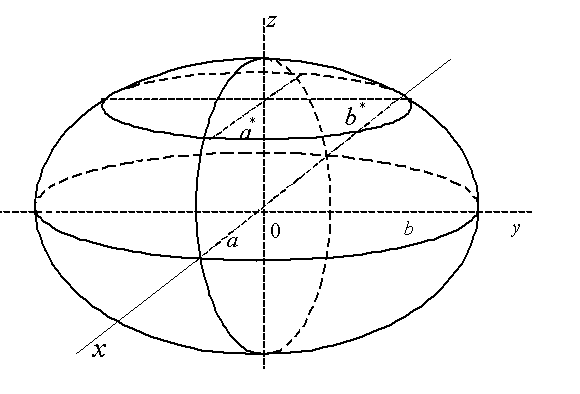 Исследуем форму эллипсоида. В уравнение (1) переменные Из уравнения эллипсоида Найдем сечения эллипсоида его плоскостями симметрии и изобразим исследуемую поверхность. Плоскость 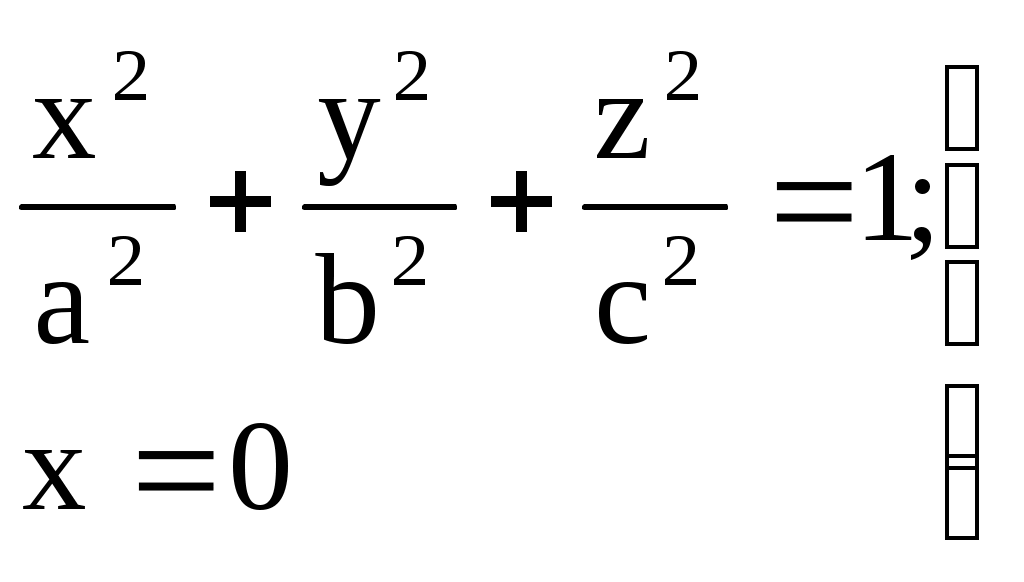 или или 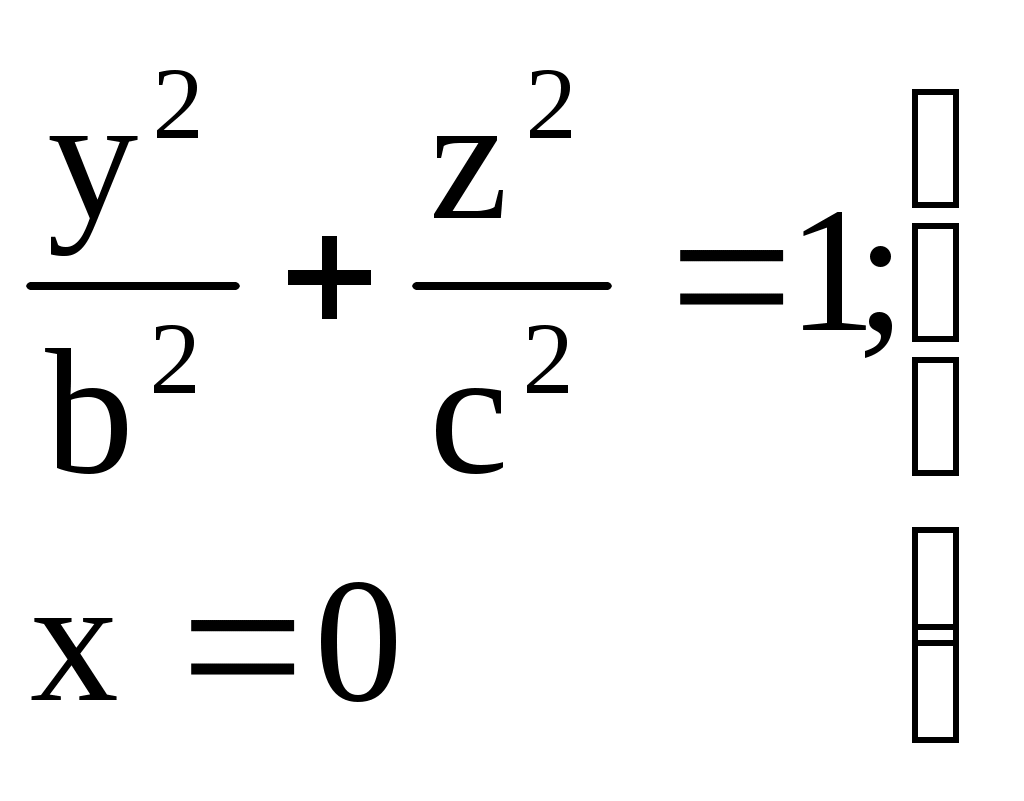 плоскость 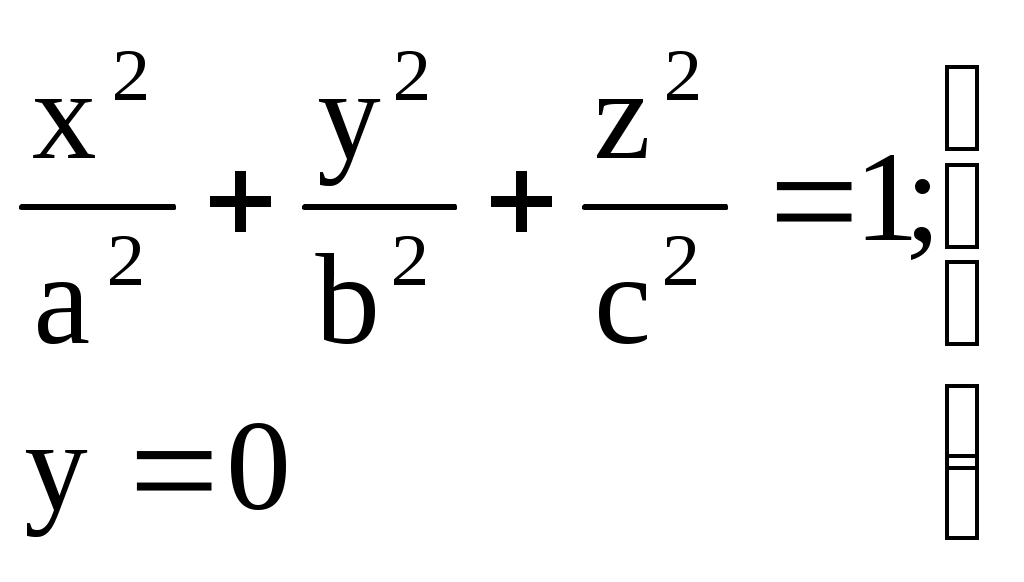 или или 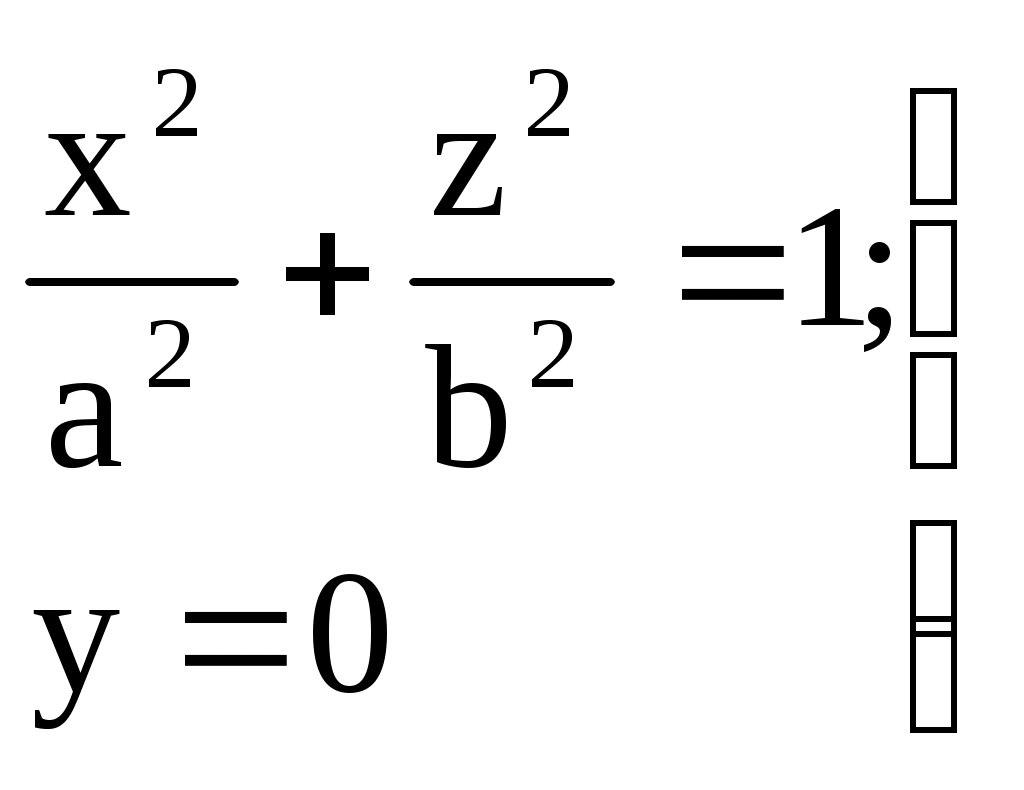 плоскость 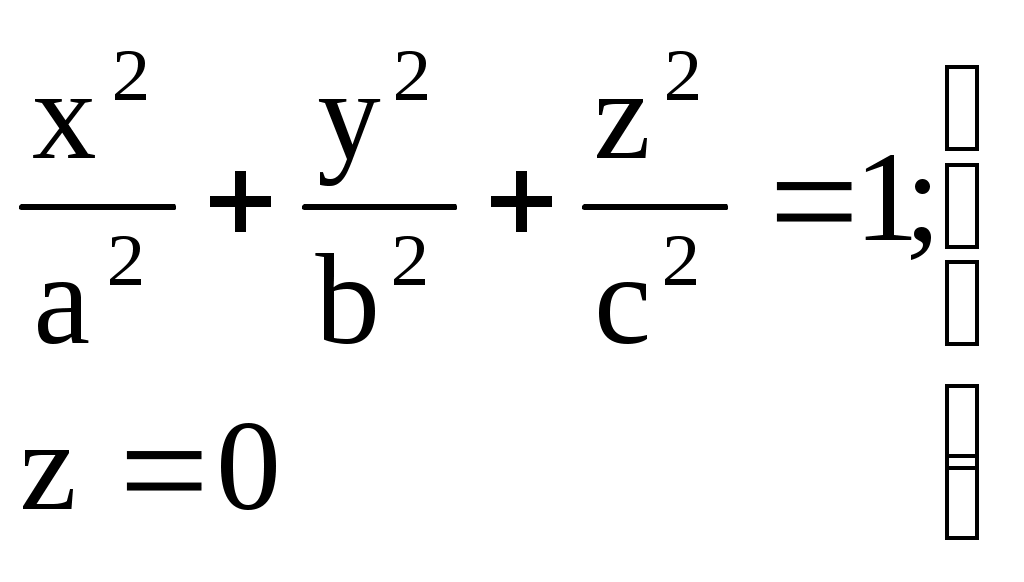 или или 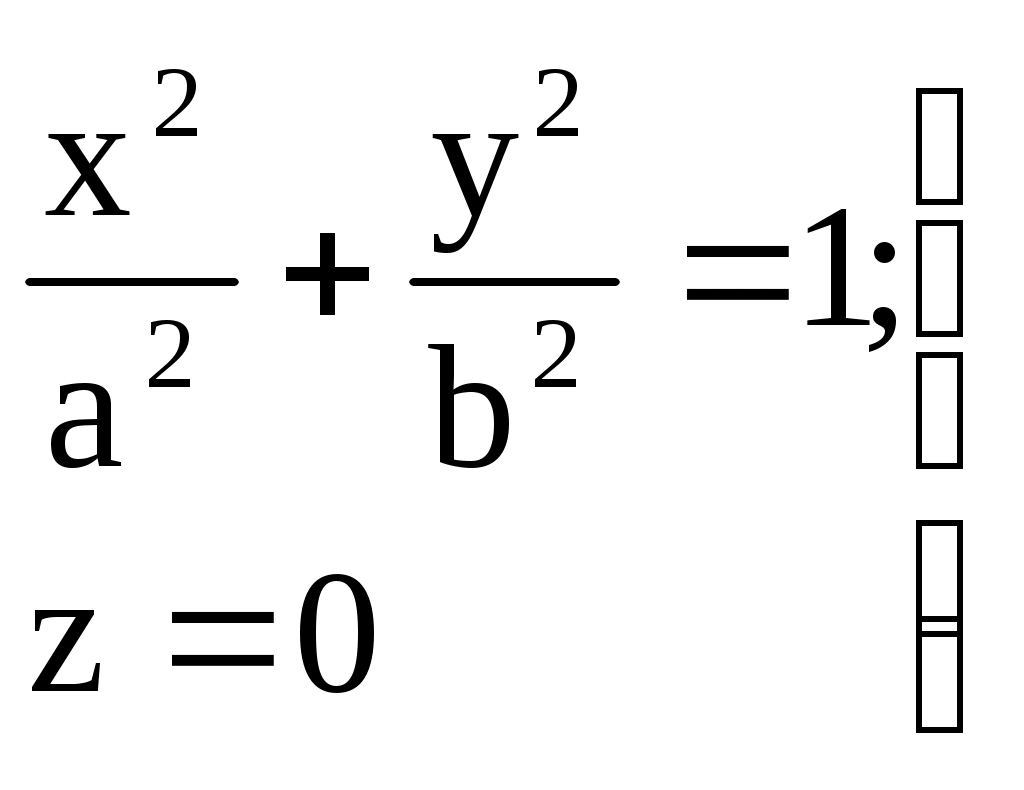 В сечениях эллипсоида координатными плоскостями мы получили эллипсы. Рассмотрим сечения эллипсоида плоскостями, параллельными координатным плоскостям. Найдём сечения эллипсоида плоскостью, параллельной плоскости 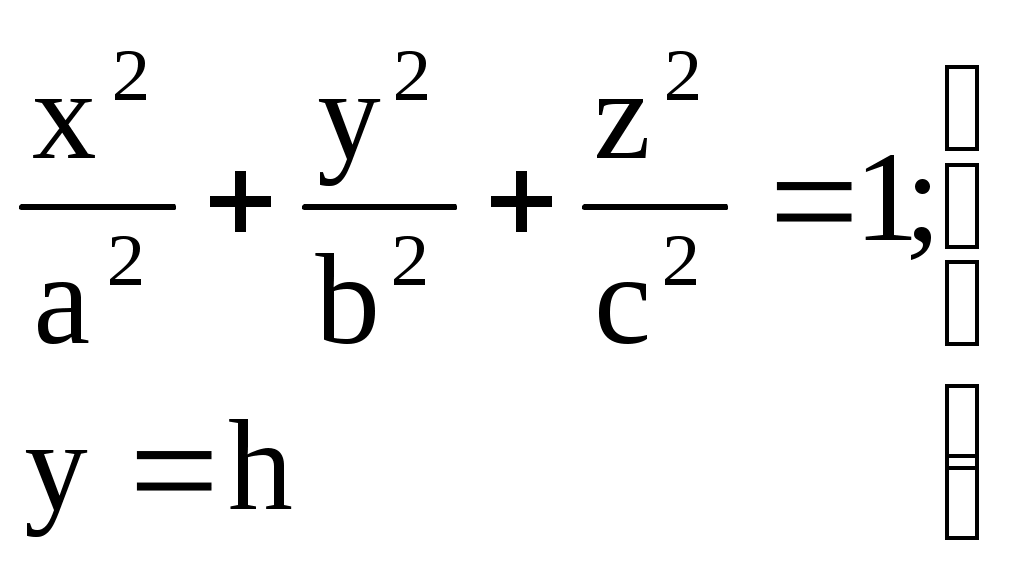 или или 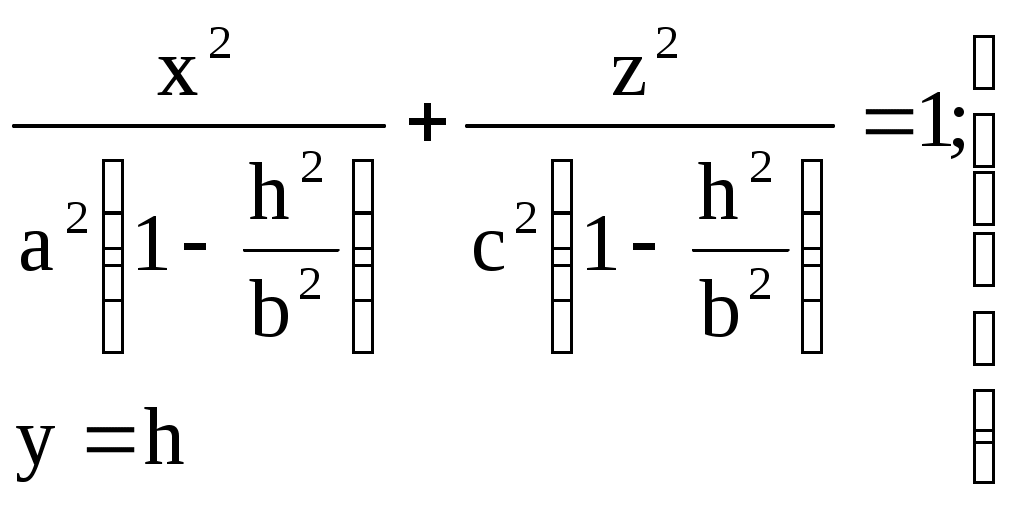 При Аналогичная картина наблюдается при пересечении эллипсоида плоскостями, параллельными плоскостями Если для эллипсоида Это сфера, центр которой совпадает с началом координат и радиус равен 31.Гиперболоиды Существуют два вида гиперболоида: однополостный и двуполостный. Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением Двуполостным гиперболоидом называется поверхность, определяемая уравнением 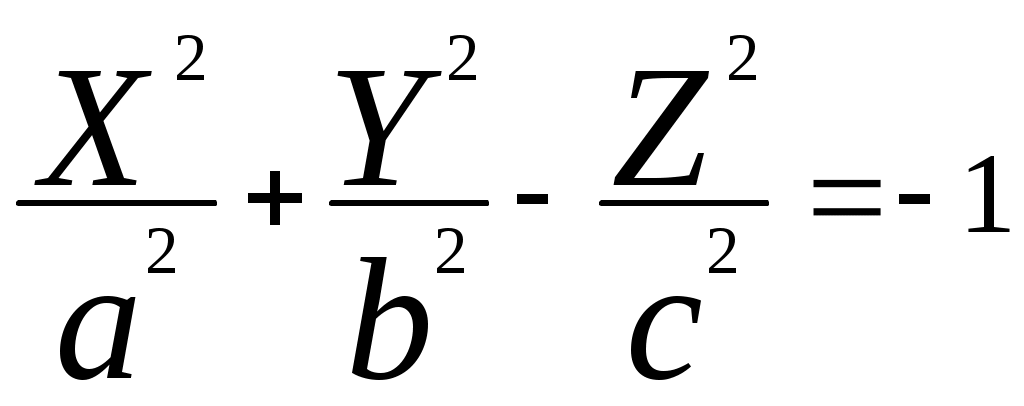 (3) (3)Исследуем форму однополостного гиперболоида. Так как в уравнение (2) переменные x, y и z входят только во второй степени, то это значит, что однополостный гиперболоид, определяемый уравнением (2), симметричен относительно всех трех координатных плоскостей, координатных осей и начала координат. Из уравнения (2) следует, что поверхность не пересекает оси Oz, которая является поэтому мнимой осью поверхности. Каждую из осей Ox и Oy однополостный гиперболоид пересекает в двух точках: Найдем сечения однополостного гиперболоида его плоскостями симметрии и плоскостями, им параллельными. 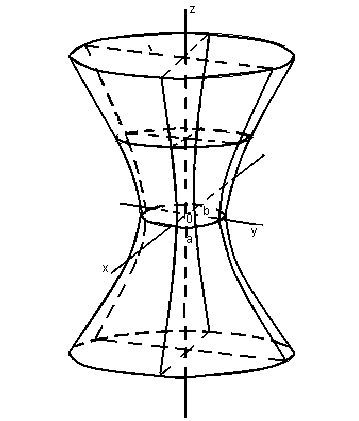 Плоскость yOz пересекает однополостный гиперболоид по гиперболе и 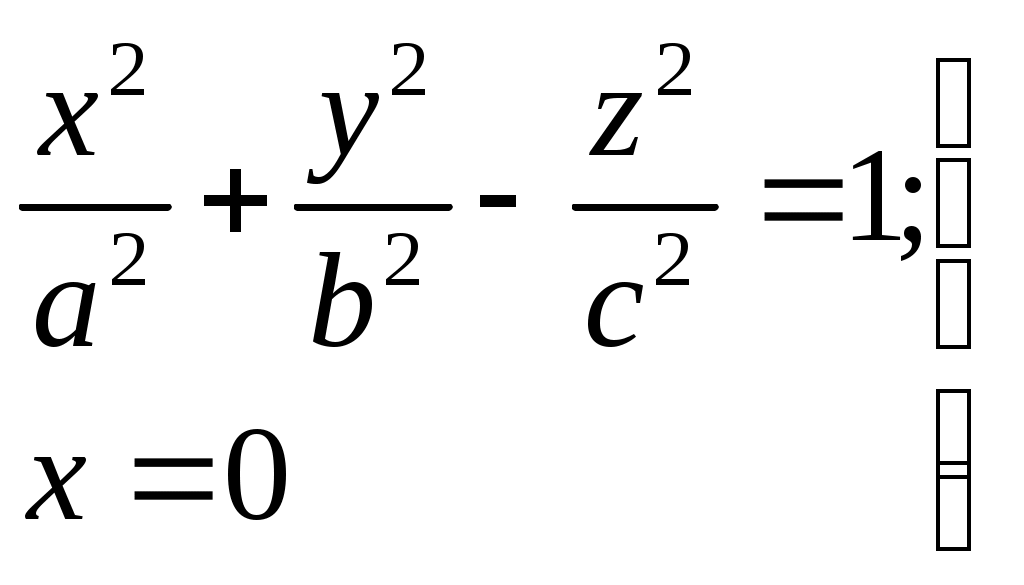 ли ли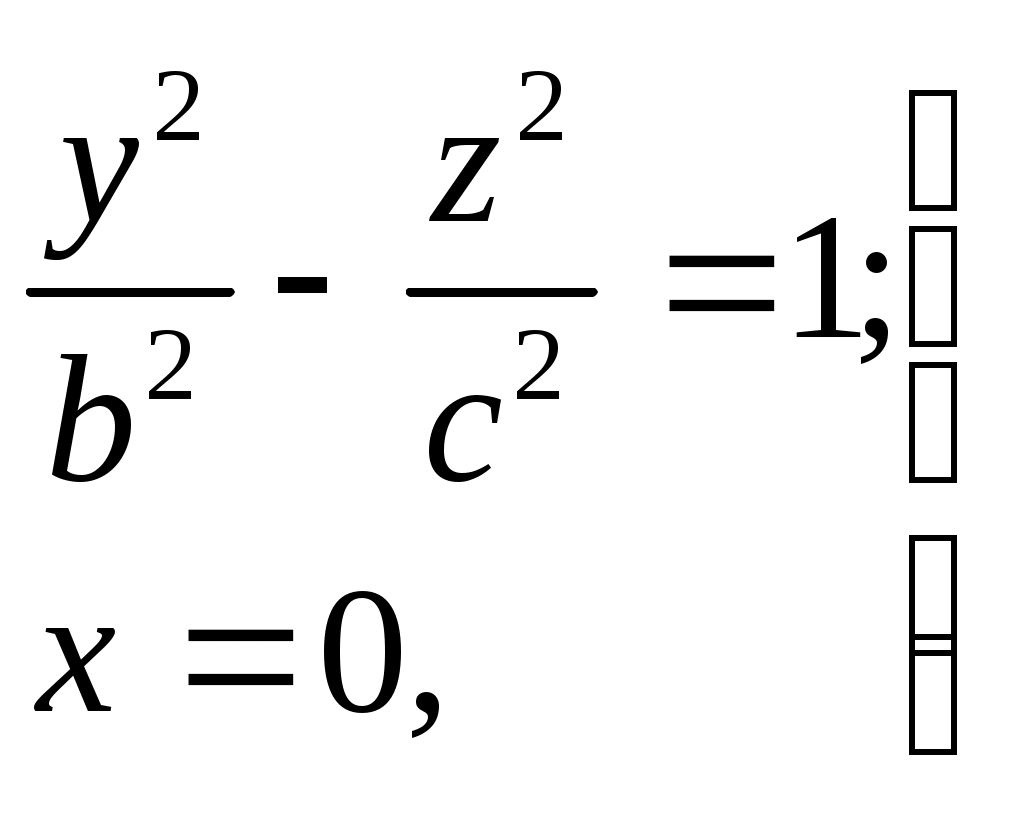 плоскость xOy –по эллипсу 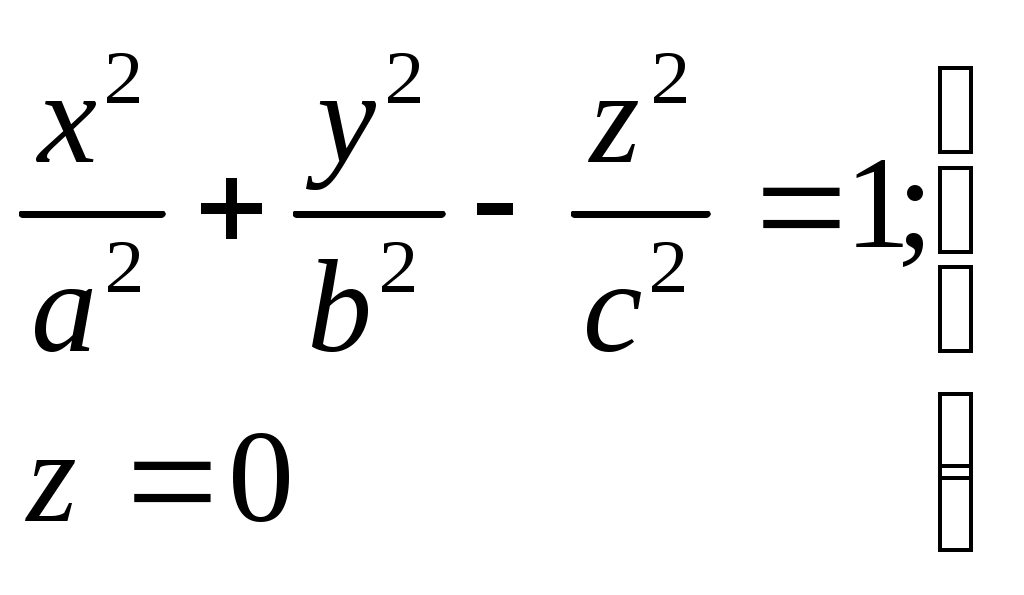 или или 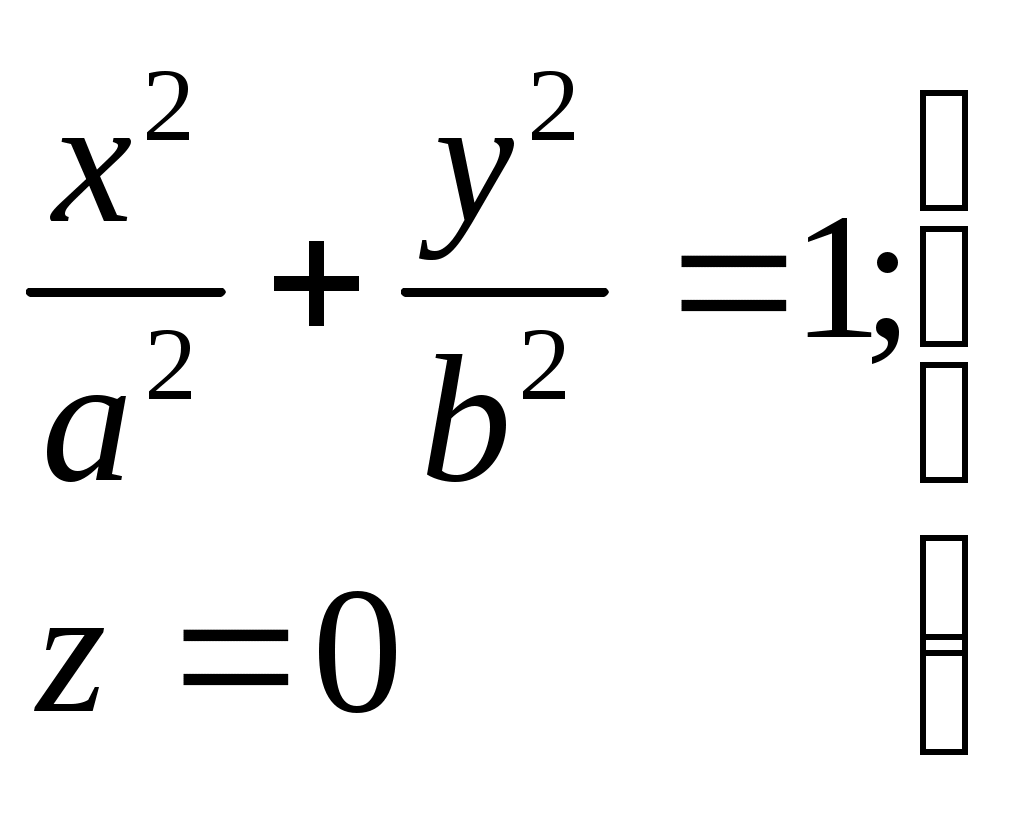 а плоскость xOz –по гиперболе 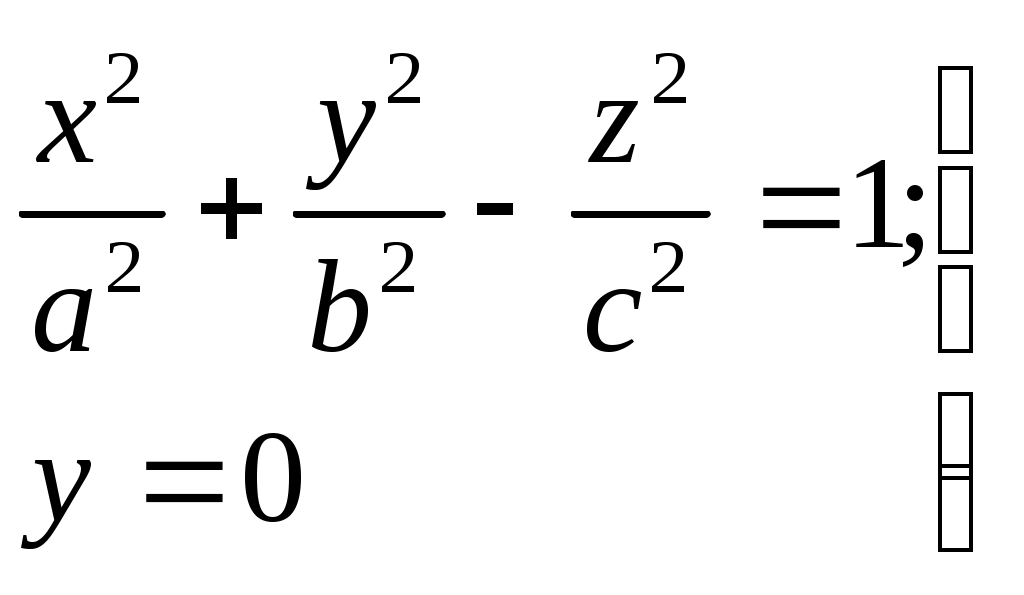 или или 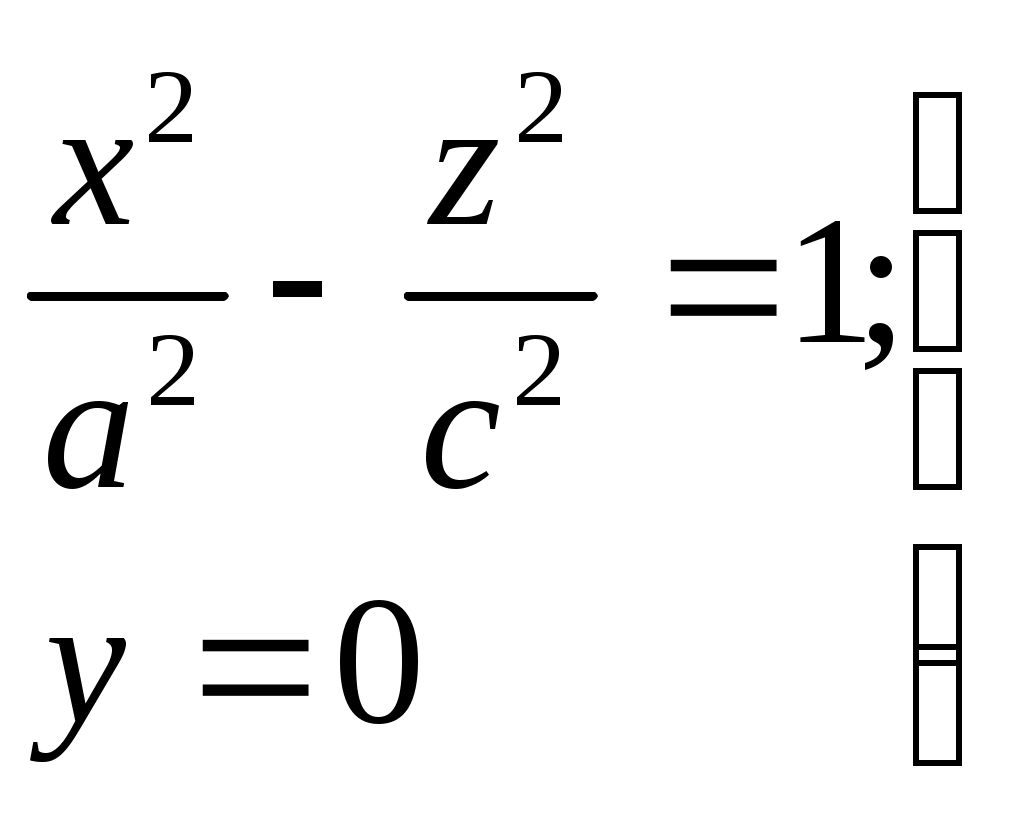 Плоскость z=h пересекает однополостный гиперболоид по эллипсу 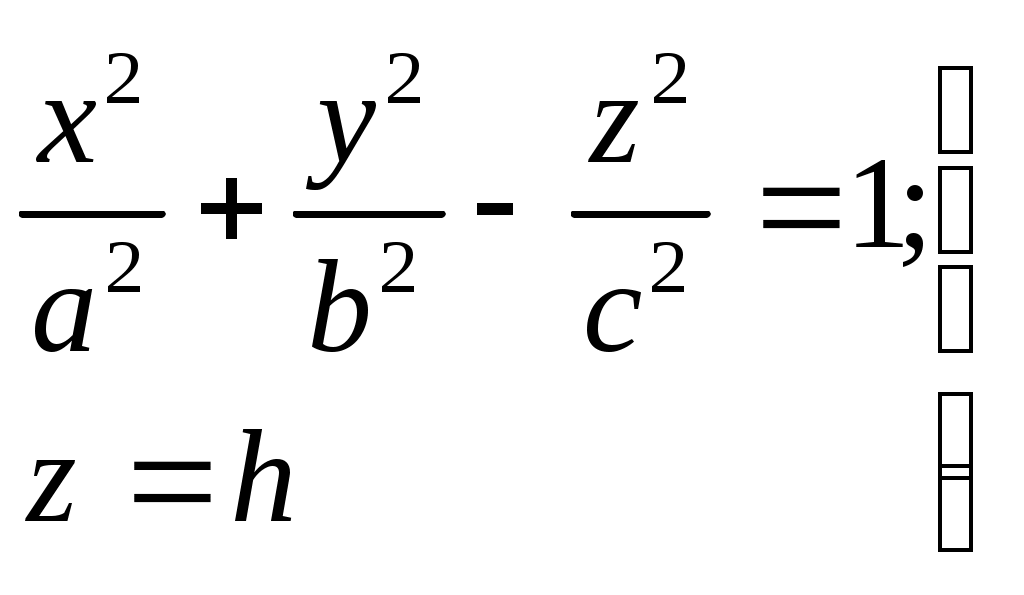 или или 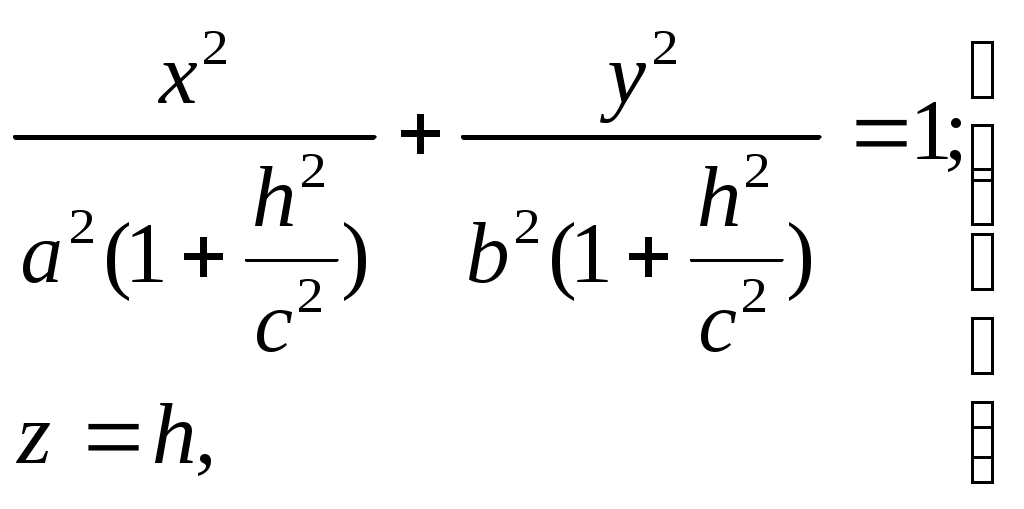 полуоси которого увеличиваются с увеличением Плоскость x = һ пересекает однополостный гиперболоид по линии 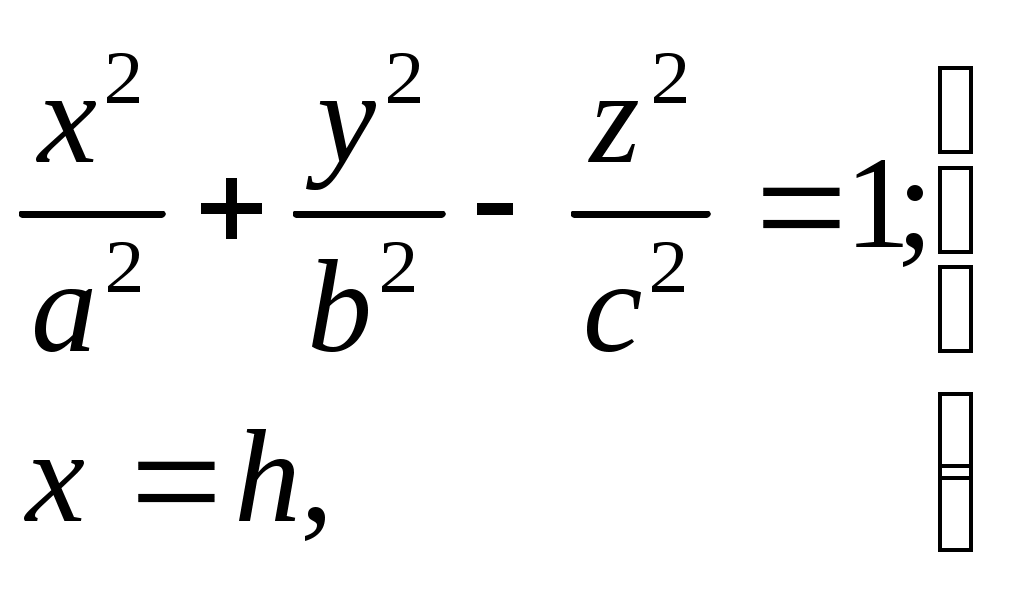 или или 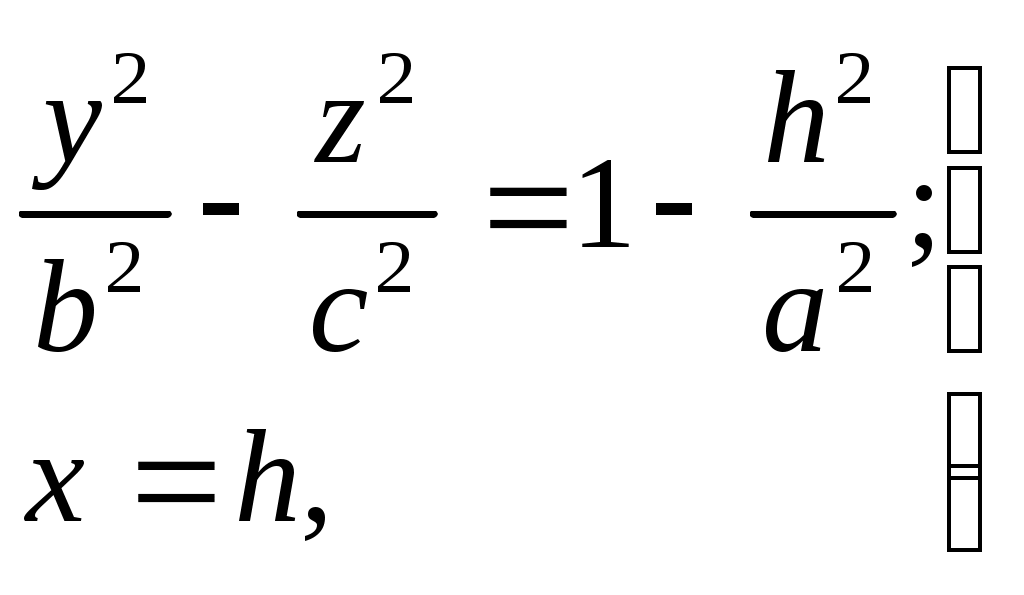 или 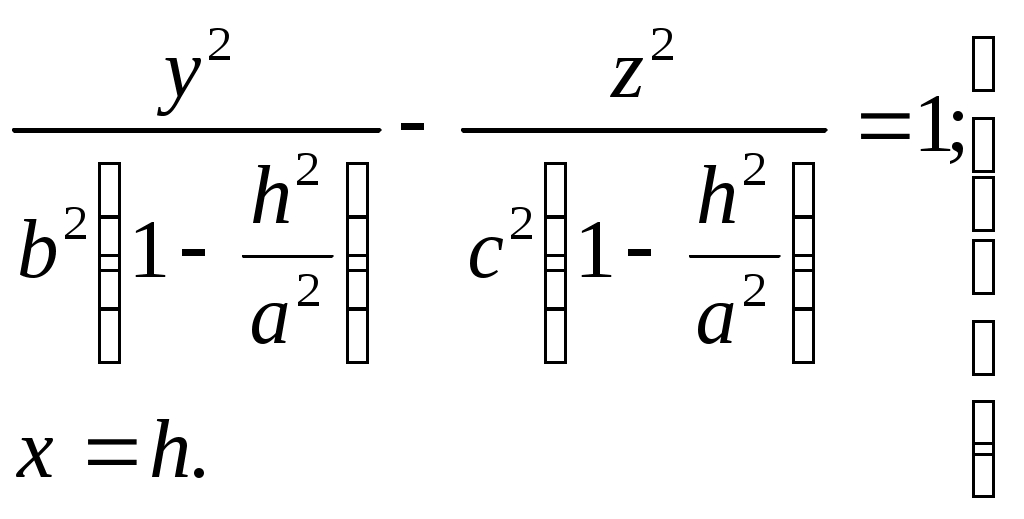 Если 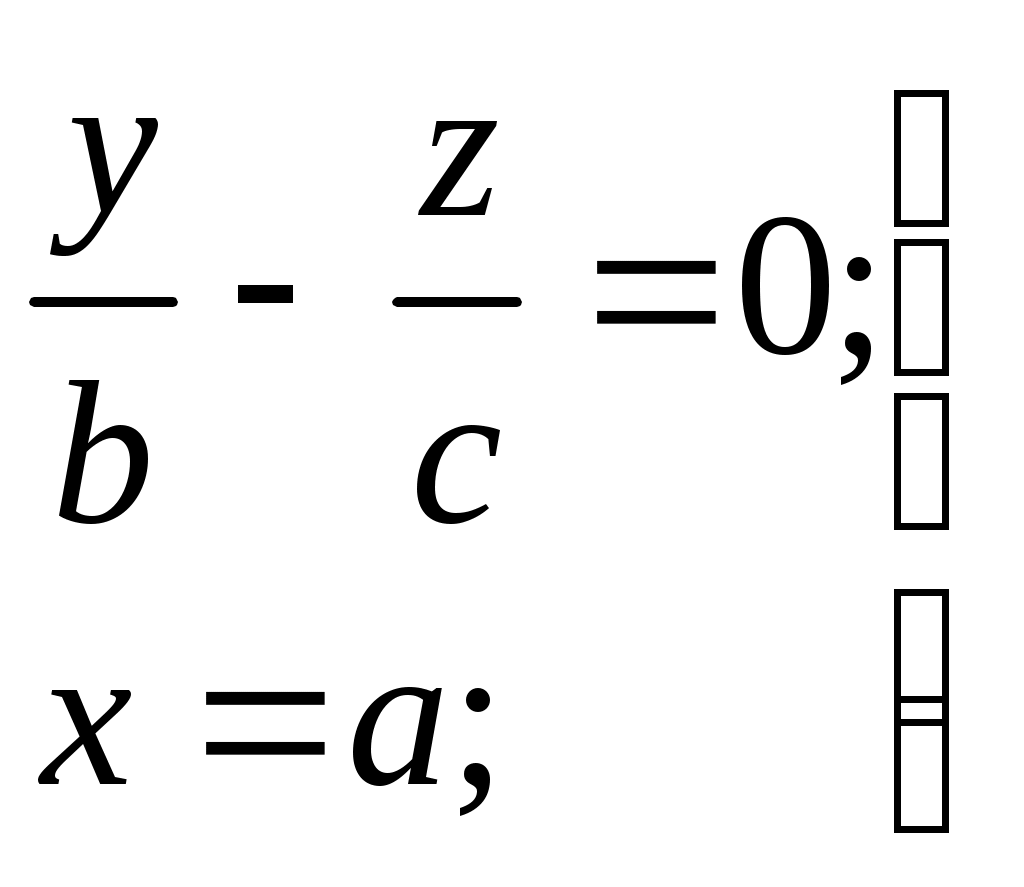 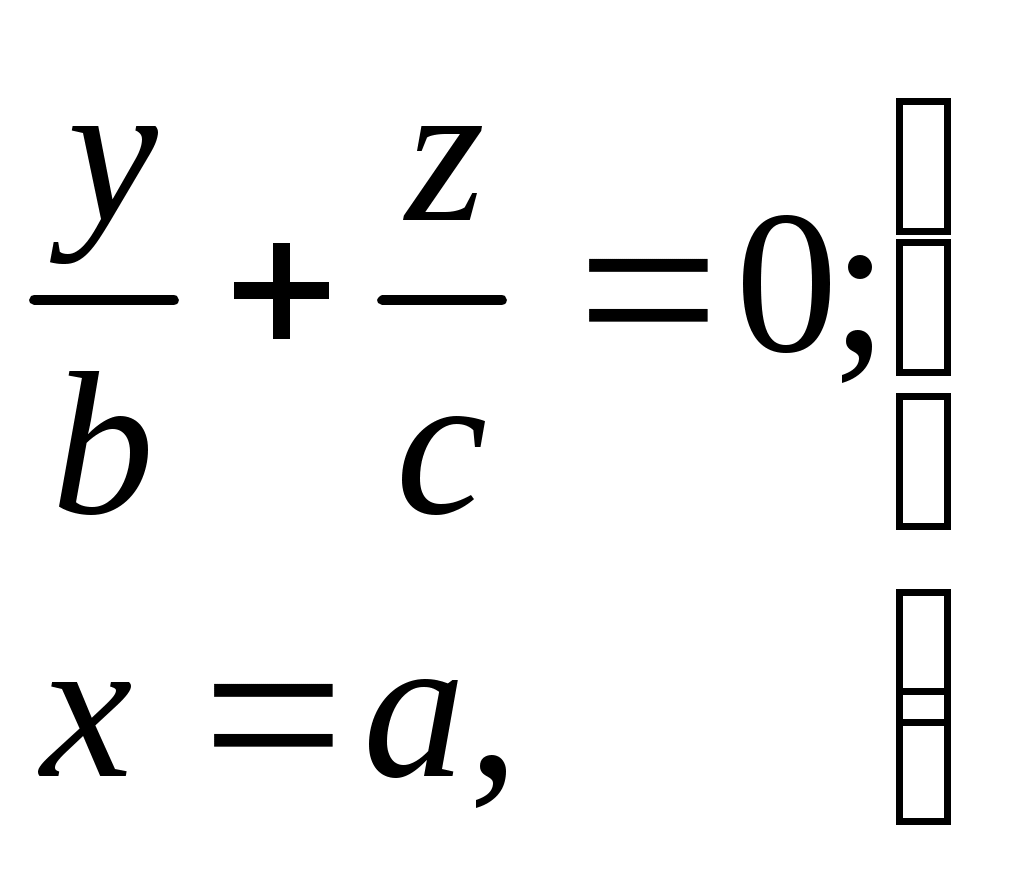 или 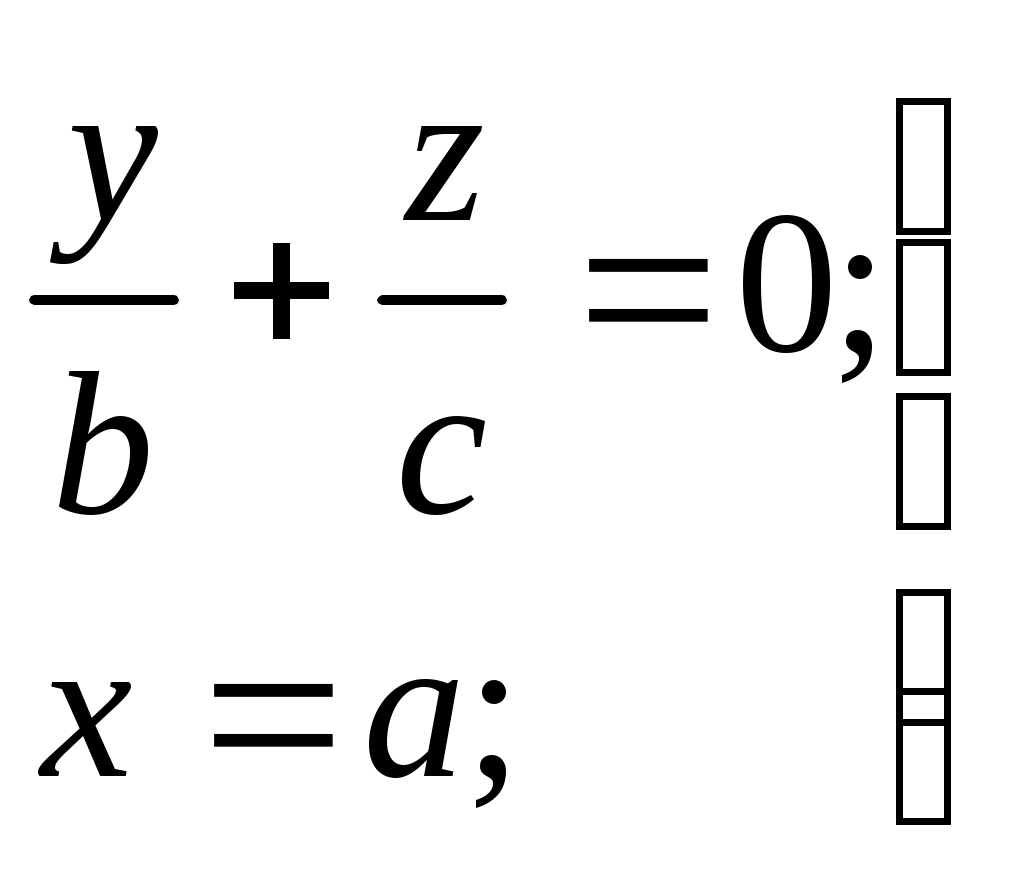 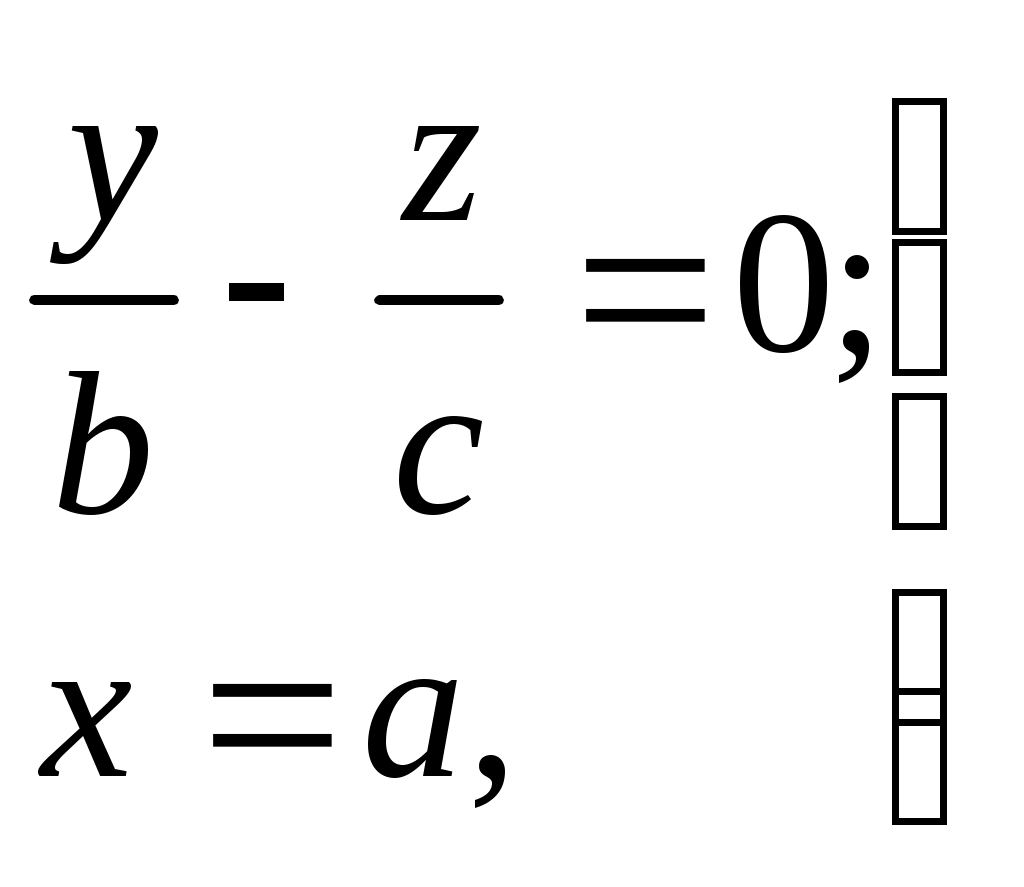 которые называются прямолинейными образующими однополостного гиперболоида. Если же Аналогичная картина получается при пересечении поверхности плоскостями, параллельными плоскости хОz . Исследуем форму двуполостного гиперболоида. Так как в уравнение (3) поверхности переменные X, Y, Z входят только во второй степени, это значит, что поверхность симметрична относительно всех координатных плоскостей, координатных осей и начала координат. Из уравнения (3) следует, что поверхность не пересекает осей OY и OZ, а ось OX пересекает в двух точках: Найдем сечения двуполостного гиперболоида его плоскостями симметрии и плоскостями, им параллельными. 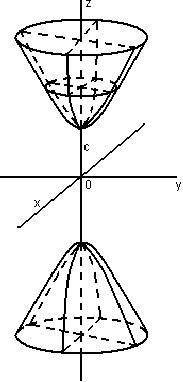 Плоскость ХОY пересекает двуполостный гиперболоид по гиперболе 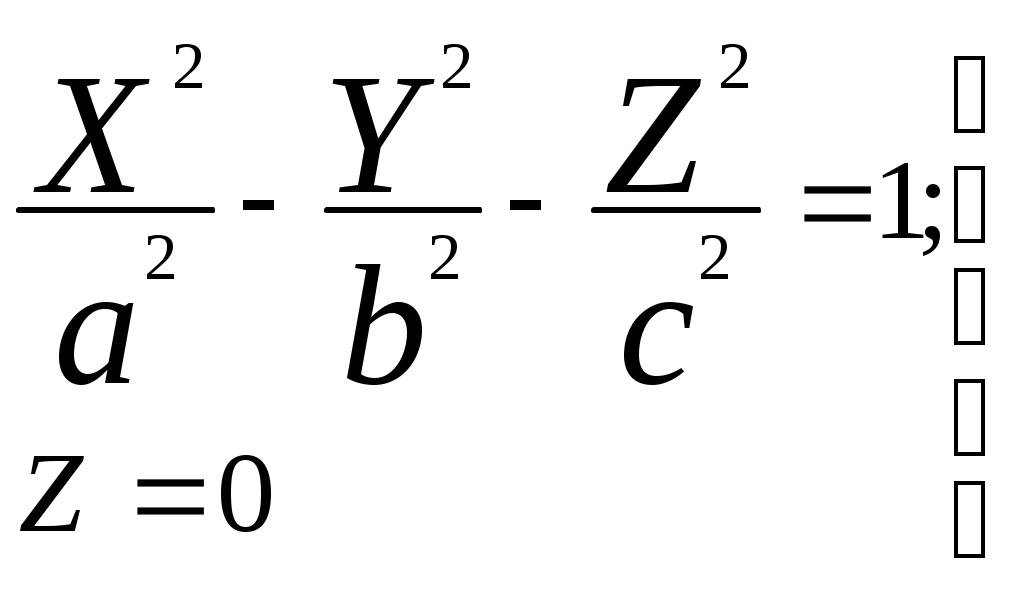 или или 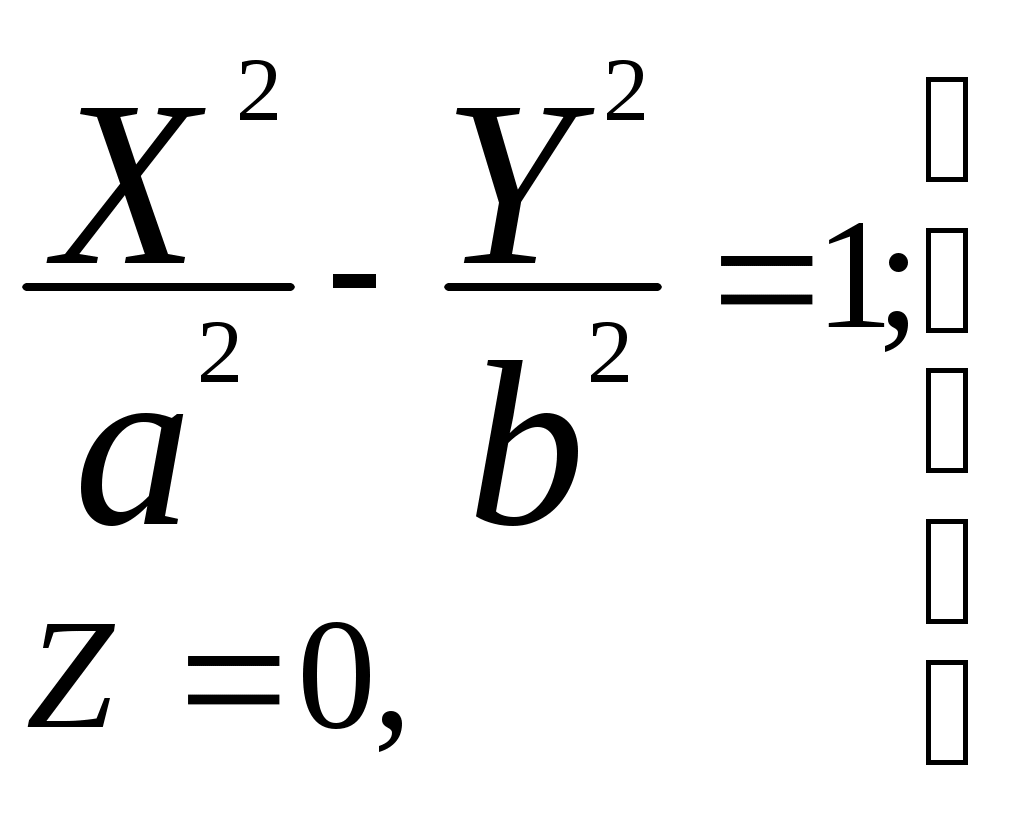 плоскость XOZ - по гиперболе 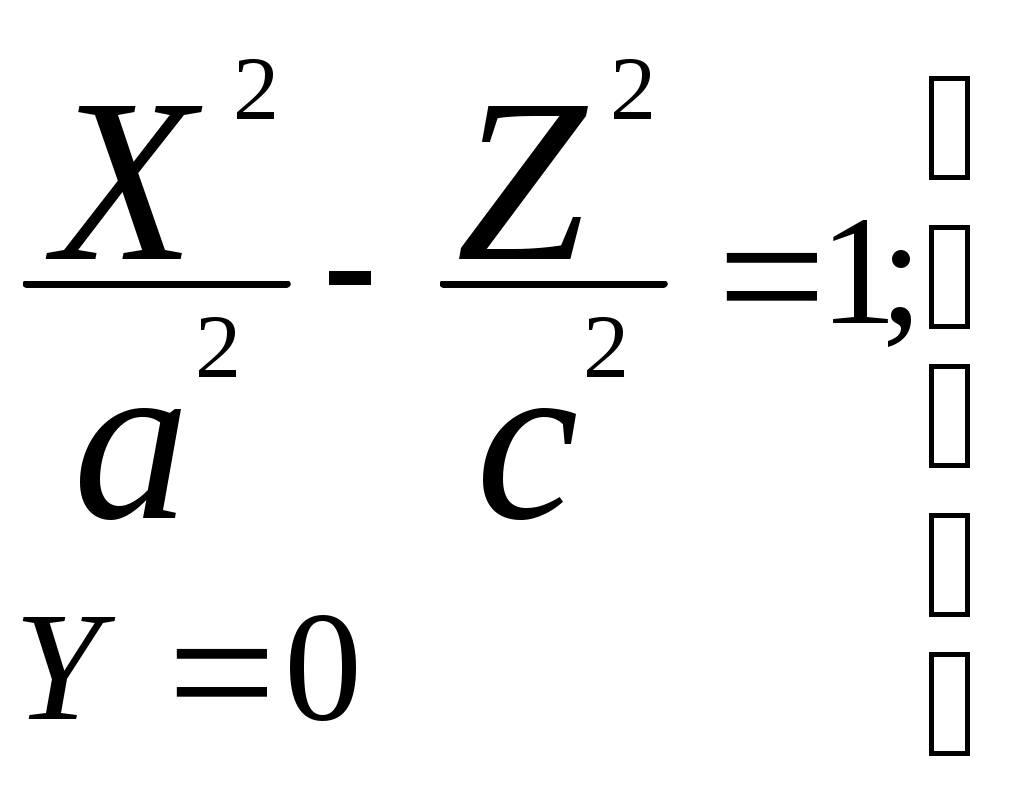 или или 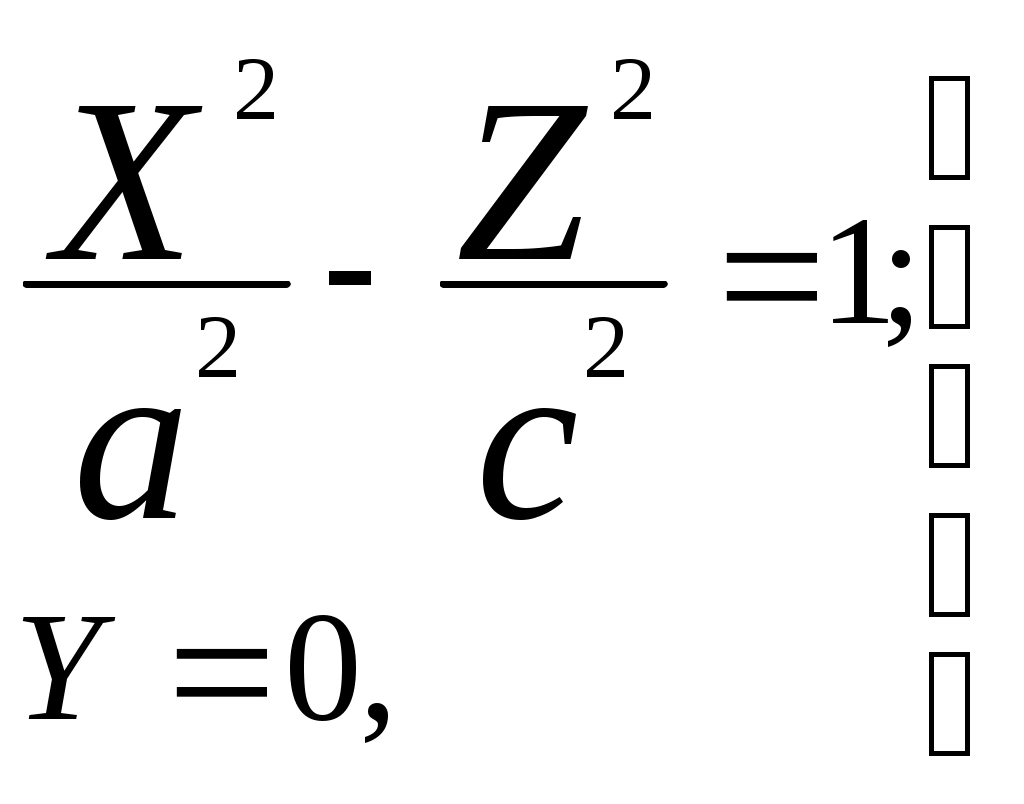 а плоскость Х=h – по линии 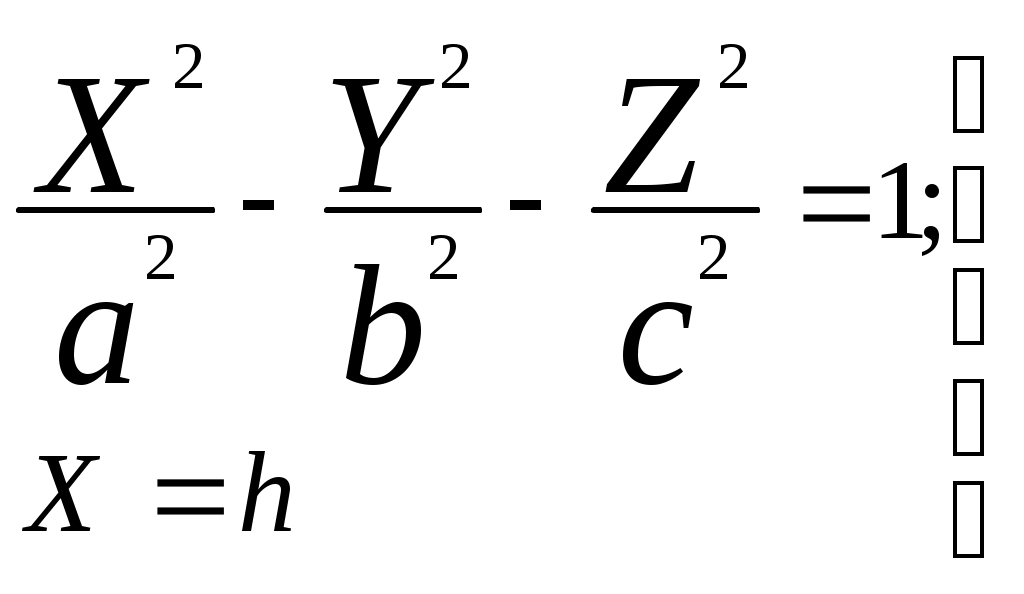 или или 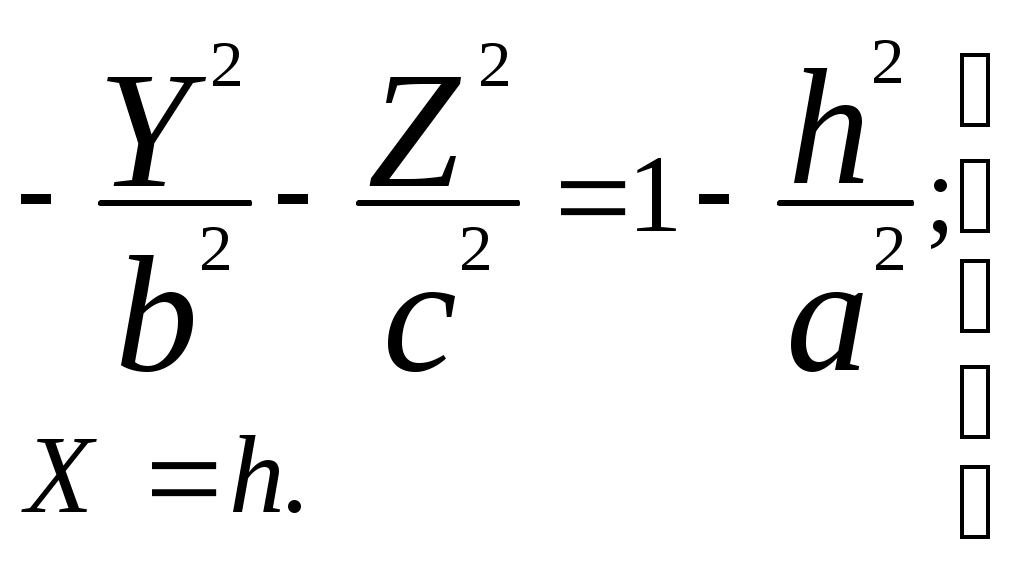 Если Если 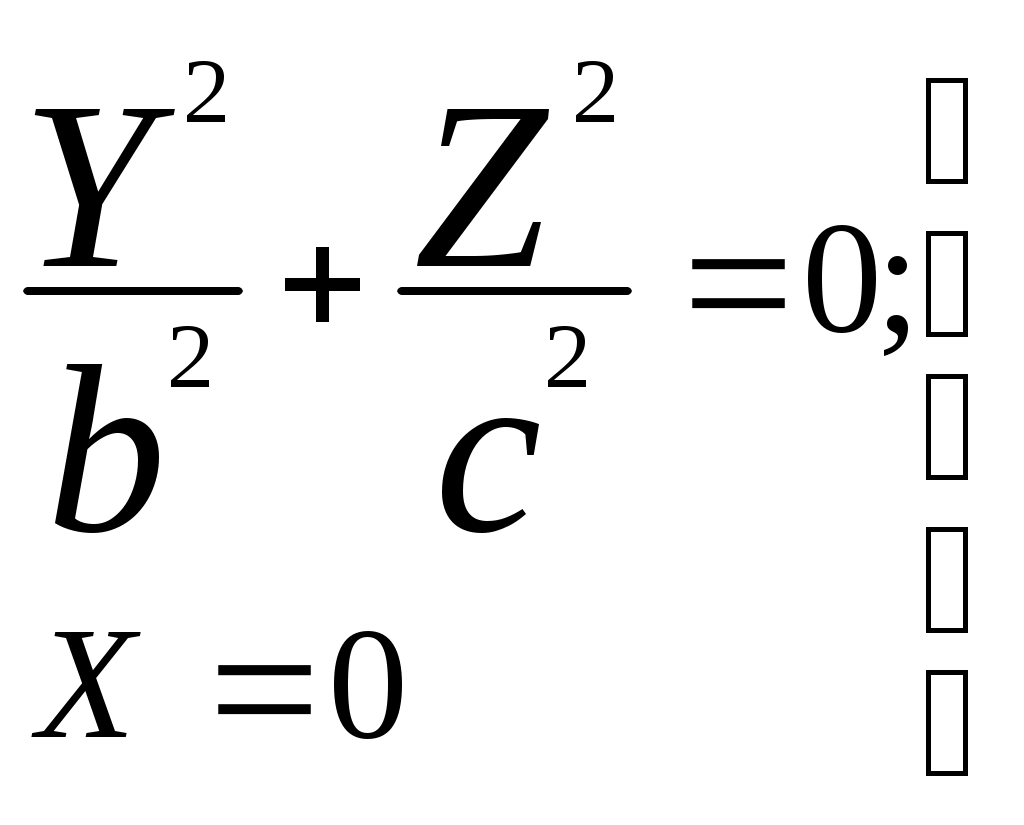 Значит, плоскость касается поверхности в одной точке – вершине двуполостного гиперболоида. Если 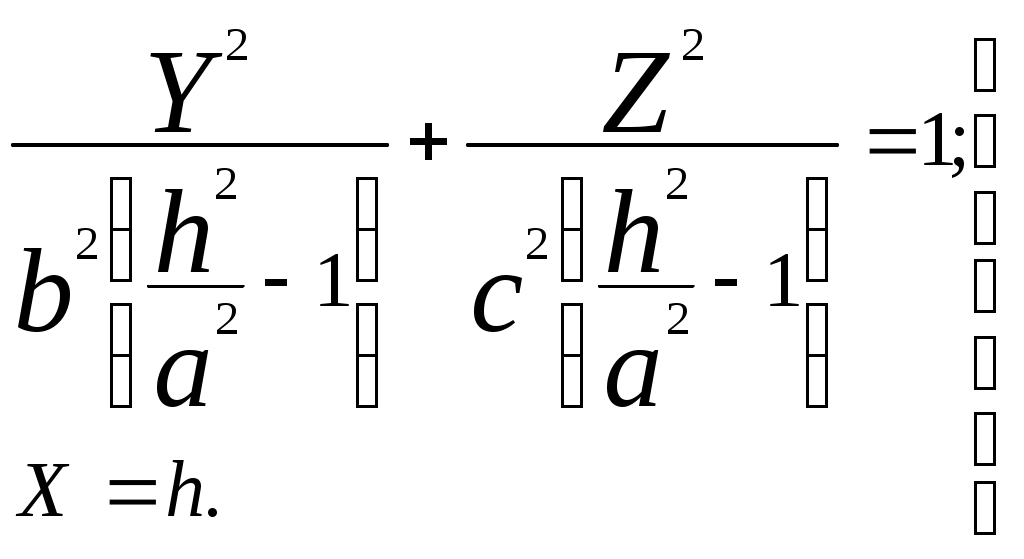 В сечении получаем эллипс, оси симметрии которого параллельны осям OY и OZ, а полуоси увеличиваются с увеличением 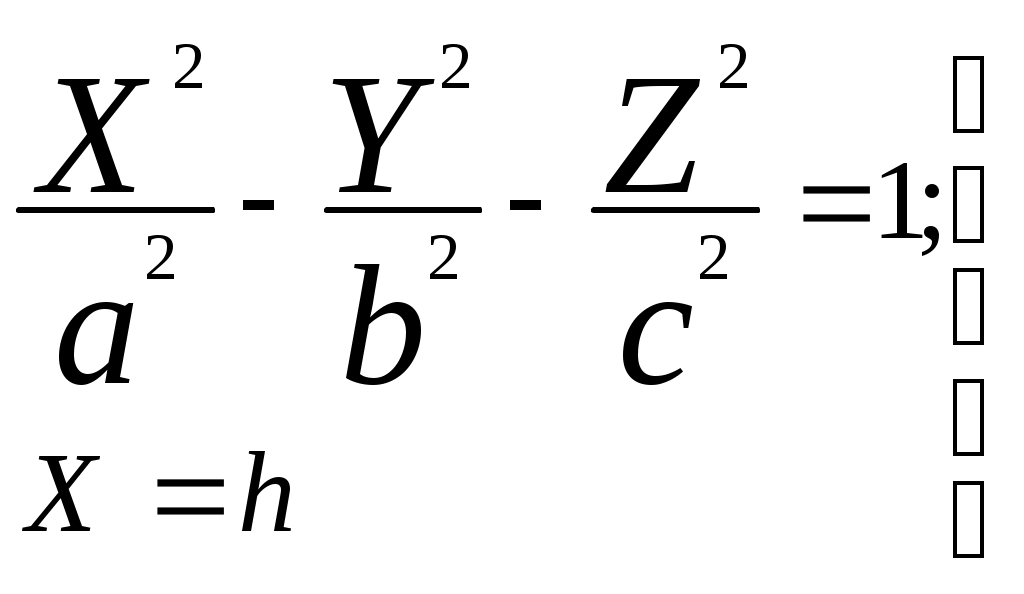 или или 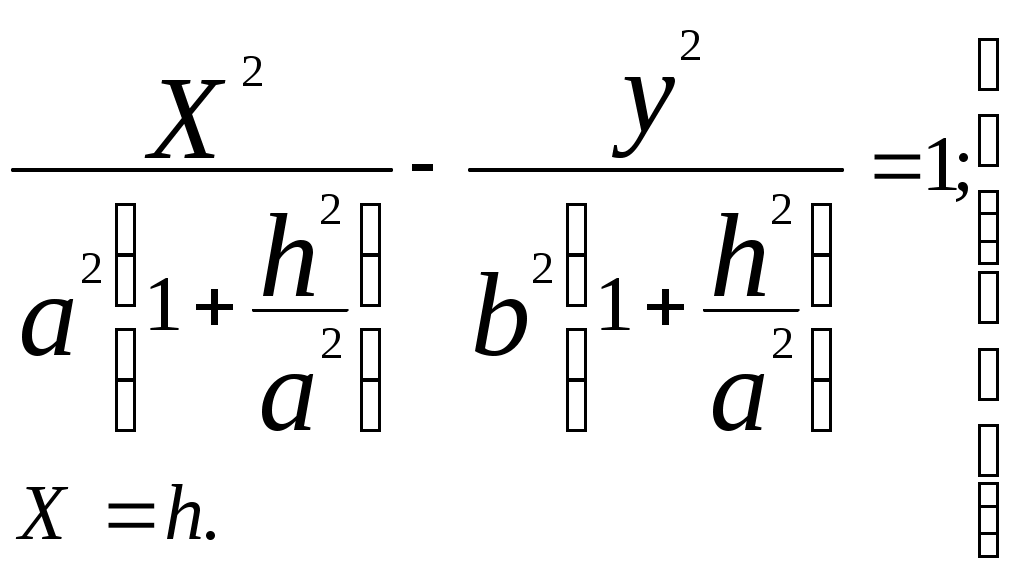 В сечении получаем гиперболу, действительная ось которой параллельна оси ОХ. Аналогично плоскость Y=h пересекает двуполостный гиперболоид по гиперболе, действительная ось которой параллельна оси ОХ: 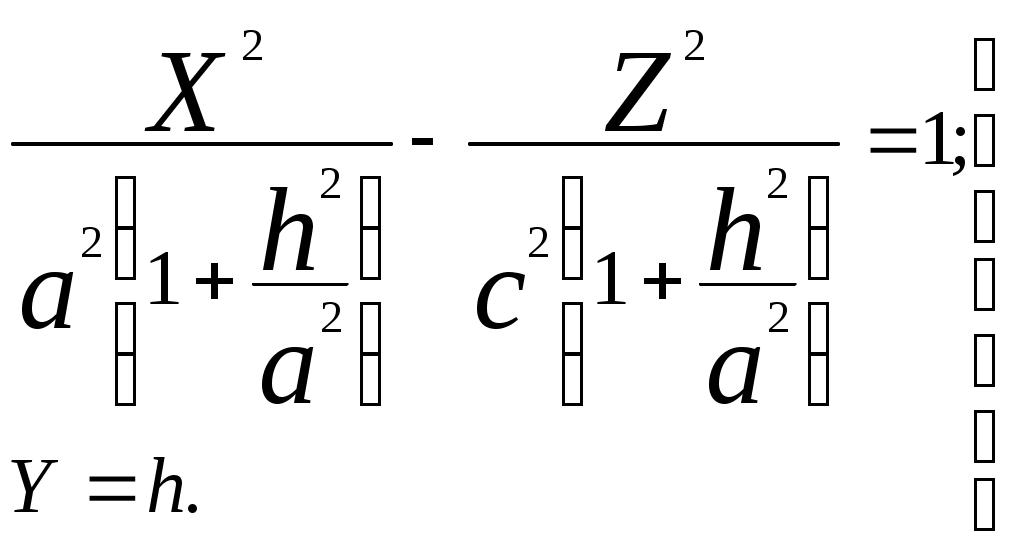 |
