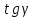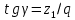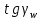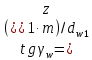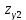Курсовая работа по деталям машин. ПЗ без подписи. Курсовой проект по дисциплине Детали машин и основы конструирования
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
2.2. Червячная передача2.2.1 Исходные данные для расчёта червячной передачиВращающий момент на колесе расчитывается по следующей формуле: 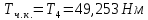 (2.18) (2.18)Материал, выбранный для изготовления венца черевячного колеса: БрАЖ9-4Л. Допускаемые контактные напряжения для данного материала: [Ϭн]=200МПа. Допускаемые напряжения изгиба: [Ϭf0]=108МПа; [Ϭf1]=83МПа; [Ϭв]=236МПа; [ϬТ]=490МПа. Допускаемые напряжения для проверки прочности зубьев черевячных колес: а)контактные : [Ϭн]мах=2  [ϬТ] = 980 МПа; [ϬТ] = 980 МПа;б)изгибные : [Ϭf]мах=0,8  [Ϭт] = 392 МПа. [Ϭт] = 392 МПа.Коэффициент нагрузки, используемый в расчётах: k=1,25. Материала, выбранный для изготовления червяка: 40Х. 2.2.2. Выбор числа заходов червяка z1По ГОСТ 2144–74 допускает выбор числа заходов из значений z1 = 1, 2, 4. При u = 30…60 рекомендуется принять z1 = 2, а при u > 60 – z1 = 1. Следовательно, исходя из данных условий для конкретной расчетной схемы выбираем 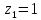 . .2.2.3. Определение числа зубьев колеса z2Определение числа зубьев колеса z2 осуществляется по формуле: 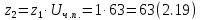 Наименьшее число зубьев колеса, при котором не подрезаются зубья при нарезке (для профильного угла α = 20° и высоте головки, равной модулю), равно z2= 27. Таким образом, даже при наименьшем передаточном числе u = 8, допускаемом ГОСТ 2144–76, подрезания зубьев при z1 = 1 не будет. 2.2.4. Определение коэффициента диаметра червяка qОпределение коэффициента диаметра червяка q осуществляется по графикам (рис. 4) таким образом, чтобы коэффициент деформации червяка θ удовлетворял условию: 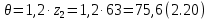 При этом следует руководствоваться таблицей стандартных значенийq по ГОСТ 19672 – 74 (табл.3) Таблица 3
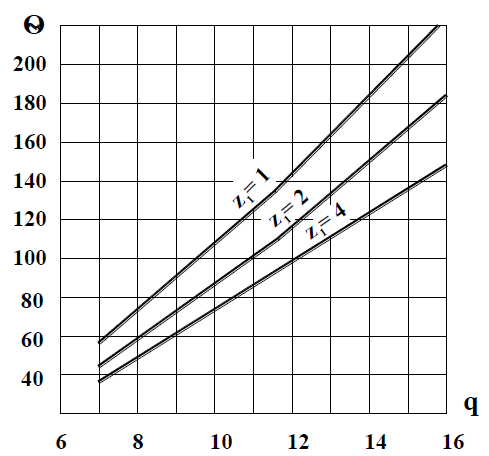 Рисунок 2.2. Зависимость коэффициента деформации θ от коэффициента диаметра червяка q числа заходов z1 Из таблицы 1 определяем, что q=8. 2.2.5. Определение межосевого расстоянияв передаче осуществляется по допускаемым контактным напряжениям по формуле (мм): 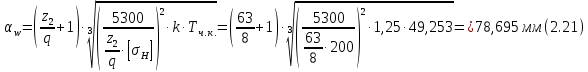 2.2.6. Определение модуля зацепления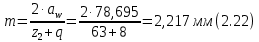 По найденной величине m выбираем из ГОСТ 19672–74 ближайшее большее стандартное значение модуля, равное 2,5 (по ГОСТ). Уточнение межосевого расстояния в соответствии со стандартным модулем производится по формуле: 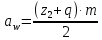 = = 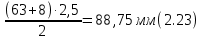 2.2.7. Определение основных геометрических параметров передачи:Таблица 4. Червячная передача
Где Z  число зубьев; число зубьев; делительный диаметр; делительный диаметр;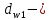 начальный диаметр; начальный диаметр;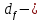 диаметр впадин; диаметр впадин;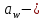 межосевое расстояние; межосевое расстояние;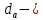 диаметр вершин; диаметр вершин;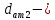 наибольший диаметр колеса; наибольший диаметр колеса; ; ;b2 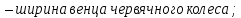 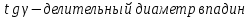 ; ;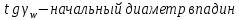 . . 2.2.8 Определение действующих контактных напряженийОпределение действующих контактных напряжений(H/мм2) и оценка работоспособности передачи по контактным напряжениям производится по формуле: 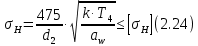 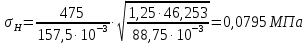 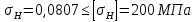 - условие выполняется - условие выполняется2.2.9 Определение сил, действующих в зацеплении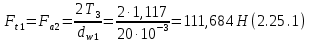 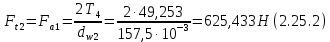 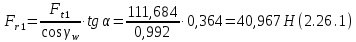 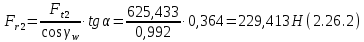 где Ft1 и Fa1 – окружная и осевая силы на червяке; Ft2 и Fa2 – окружная и осевая силы на колесе; Fr – радиальная сила на червяке и колесе; T2 – вращающий момент на колесе; Т1 – вращающий момент на червяке, α = 20° – профильный угол червяка. 2.2.10 Проверка изгибной выносливости зубьев колеса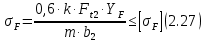 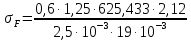 =20,94 Мпа =20,94 Мпа20,94 МПа 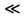 392 Мпа – условие выполняется. 392 Мпа – условие выполняется.где F – действующее, а F – допускаемое значение изгибных напряжений, Н/мм2; k – коэффициент нагрузки; Ft2 – окружное усилие на колесе, Н; m– принятый стандартный модуль, мм; b2– ширина венца червячного колеса, мм; YF – коэффициент формы зубьев (определяется по табл. 4). Для эквивалентного колеса число зубьев рассчитывается по формуле 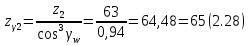 Таблица 5 Коэффициент формы зубьев для червячных колёс
2.3. Расчёт валов редуктораПостроив по полученным размерам шестерен и колес приблизительный облик редуктора, необходимо рассчитать диаметры валов, на которые, соответственно, крепятся элементы передач. Сперва подбирают материалы валов, после – рассчитывают их на прочность, строя эпюры поперечных сил и изгибающих моментов. Из условия прочности вала находится его диаметр. Для всех валов применяется сталь 40Х: σT=550 Мпа. Начальные данные: F=7H 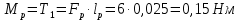 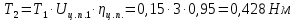 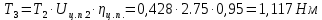 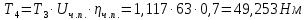 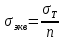 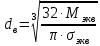 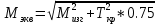 Вал 1  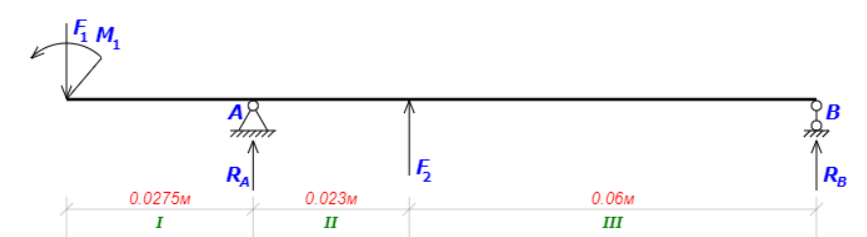 Рисунок 2.3. Схема нагружения вала 1 Реакции опор ∑MB = - RA(L - L1) + ∑qi(bi - ai)(2L - ai - bi)/2 + ∑Fi(L - ci) - ∑Mi = = - RA(L - L1) + F1(L - c1) + F2(L - c2) - M1 = - RA·(0.1105 - 0.0275) + 0.006·(0.1105 - 0) - 0.004044·(0.1105 - 0.0505) + 0.00015 = = - RA·0.083 + 0.006·0.1105 - 0.004044·0.06 + 0.00015 = = - RA·0.083 + 0.00057036 = 0 ⇒ ⇒ RA = 0.00057036/0.083 = 0.0068718 кН; Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = RB(L - L1) - ∑qi(bi - ai)(ai + bi - 2L1)/2 - ∑Fi(ci - L1) - ∑Mi = = RB(L - L1) - F1(c1 - L1) - F2(c2 - L1) - M1 = RB·(0.1105 - 0.0275) - 0.006·(0 - 0.0275) + 0.004044·(0.0505 - 0.0275) + 0.00015 = = RB·0.083 + 0.006·0.0275 + 0.004044·0.023 + 0.00015 = = RB·0.083 + 0.000408012 = 0 ⇒ ⇒ RB = -0.000408012/0.083 = -0.0049158 кН; Для проверки вычислим сумму проекций всех сил на вертикальную ось: ∑Y = RA + RB - ∑qi(bi - ai) - ∑Fi = = RA + RB - F1 - F2 = = 0.0068718 - 0.0049158 - 0.006 + 0.004044 = 0; Построение эпюр Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 0.0275): Поперечная сила Q: QI(z) = - F1 = -0.006; Значения Q на краях отрезка: QI(0) = -0.006 кН; QI(0.0275) = -0.006 кН; Изгибающий момент M: MI(z) = - F1(z - c1) + M1 = - 0.006(z - 0) - 0.00015 = -0.006z - 0.00015; Значения M на краях отрезка: MI(0) = -0.006·0 - 0.00015 = -0.00015 кНм; MI(0.0275) = -0.006·0.0275 - 0.00015 = -0.000315 кНм; Участок II (0.0275 ≤ z ≤ 0.0505): Поперечная сила Q: QII(z) = RA - F1 = 0.0068718 - 0.006 = 0.00087181; Значения Q на краях отрезка: QII(0.0275) = 0.00087181 кН; QII(0.0505) = 0.00087181 кН; Изгибающий момент M: MII(z) = RA(z - L1) - F1(z - c1) + M1 = 0.0068718(z - 0.0275)- 0.006(z - 0) - 0.00015 = 0.00087181z - 0.00033897; Значения M на краях отрезка: MII(0.0275) = 0.00087181·0.0275 - 0.00033897 = -0.000315 кНм; MII(0.0505) = 0.00087181·0.0505 - 0.00033897 = -0.00029495 кНм; Участок III (0.0505 ≤ z ≤ 0.1105): Поперечная сила Q: QIII(z) = RA - F1 - F2 = 0.0068718 - 0.006 + 0.004044 = 0.0049158; Значения Q на краях отрезка: QIII(0.0505) = 0.0049158 кН; QIII(0.1105) = 0.0049158 кН; Изгибающий момент M: MIII(z) = RA(z - L1) - F1(z - c1) - F2(z - c2) + M1 = 0.0068718(z - 0.0275)- 0.006(z - 0) + 0.004044(z - 0.0505) - 0.00015 = 0.0049158z - 0.0005432; Значения M на краях отрезка: MIII(0.0505) = 0.0049158·0.0505 - 0.0005432 = -0.00029495 кНм; MIII(0.1105) = 0.0049158·0.1105 - 0.0005432 = 0; 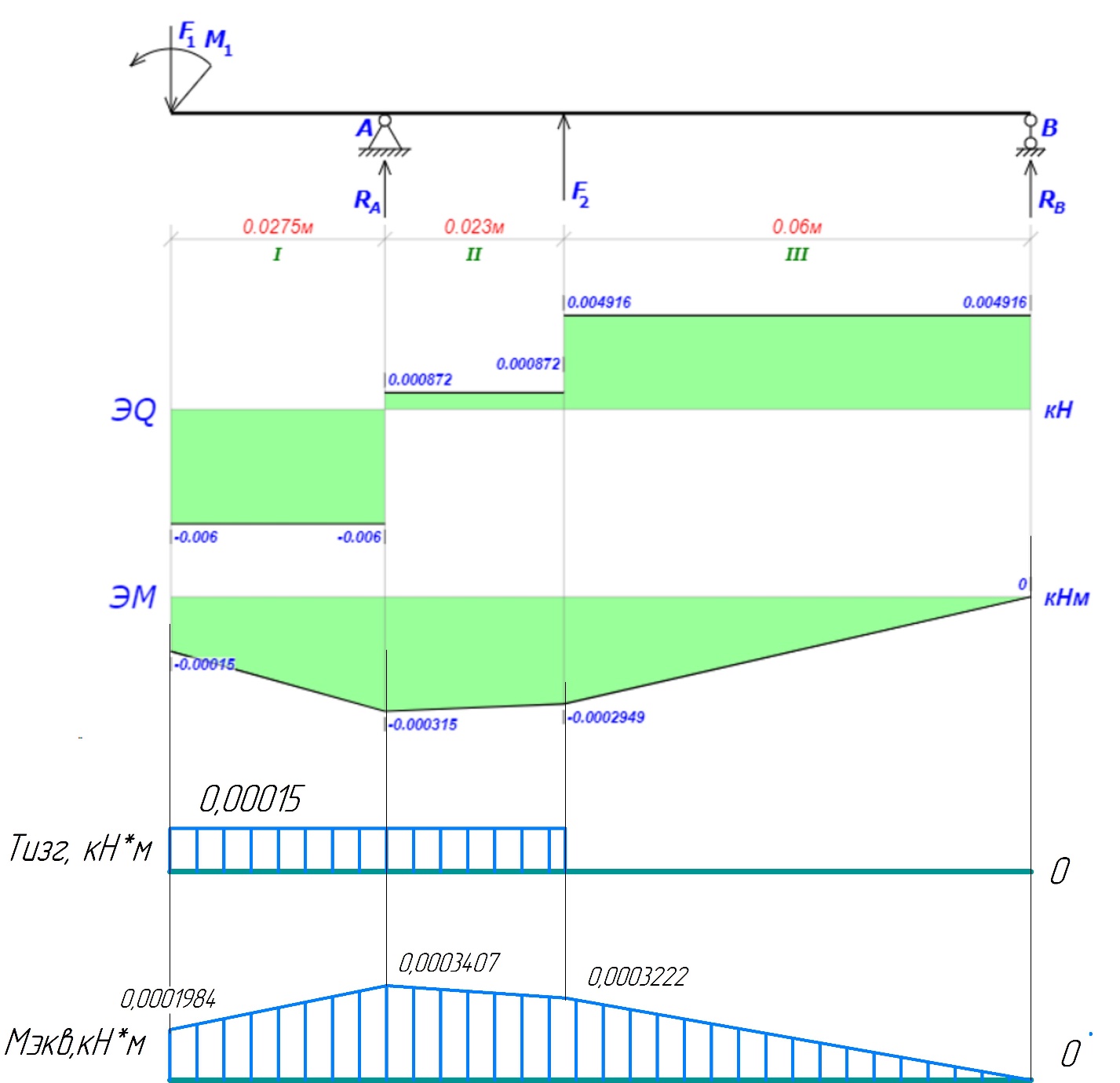 Рисунок 2.4. Эпюра сил и моментов вала 1 Построение эпюр Ткр, M(экв) 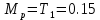 Нм=0.00015 кНм Нм=0.00015 кНм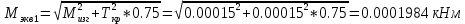 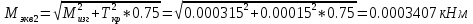 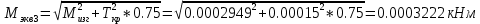 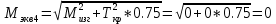 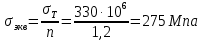 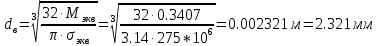 По конструкционным соображениям берём 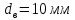 Вал 2   Рисунок 2.5. Схема нагружения вала 2 Реакции опор Сумма моментов всех сил относительно точки B должна равняться нулю: ∑MB = - RA L + ∑qi(bi - ai)(2L - ai - bi)/2 + ∑Fi(L - ci) - ∑Mi = = - RA L + F1(L - c1) + F2(L - c2) = - RA·0.083 + 0.003842·(0.083 - 0.023) - 0.00943·(0.083 - 0.0565) = = - RA·0.083 + 0.003842·0.06 - 0.00943·0.0265 = = - RA·0.083 - 1.9375· 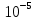 = 0 ⇒ = 0 ⇒⇒ RA = -1.9375 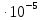 /0.083 = -0.00023343 кН; /0.083 = -0.00023343 кН;Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = RB L - ∑qi(bi - ai)(ai + bi)/2 - ∑Fici - ∑Mi = = RB L - F1c1 - F2c2 = RB·0.083 - 0.003842·0.023 + 0.00943·0.0565 = = RB·0.083 + 0.000444429 = 0 ⇒ ⇒ RB = -0.000444429/0.083 = -0.0053546 кН; Для проверки вычислим сумму проекций всех сил на вертикальную ось: ∑Y = RA + RB - ∑qi(bi - ai) - ∑Fi = = RA + RB - F1 - F2 = = -0.00023343 - 0.0053546 - 0.003842 + 0.00943 = 0; Построение эпюр Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 0.023): Поперечная сила Q: QI(z) = RA = -0.00023343; Значения Q на краях отрезка: QI(0) = -0.00023343 кН; QI(0.023) = -0.00023343 кН; Изгибающий момент M: MI(z) = RA z = -0.00023343z; Значения M на краях отрезка: MI(0) = -0.00023343·0 = 0; MI(0.023) = -0.00023343·0.023 = -5.369· 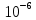 кНм; кНм;Участок II (0.023 ≤ z ≤ 0.0565): Поперечная сила Q: QII(z) = RA - F1 = -0.00023343 - 0.003842 = -0.0040754; Значения Q на краях отрезка: QII(0.023) = -0.0040754 кН; QII(0.0565) = -0.0040754 кН; Изгибающий момент M: MII(z) = RA z - F1(z - c1) = -0.00023343z - 0.003842(z - 0.023) = = -0.0040754z + 8.8366E-5; Значения M на краях отрезка: MII(0.023) = -0.0040754·0.023 + 8.8366 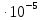 = -5.369 = -5.369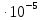 кНм; кНм;MII(0.0565) = -0.0040754·0.0565 + 8.8366 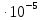 = -0.0001419 кНм; = -0.0001419 кНм;Участок III (0.0565 ≤ z ≤ 0.083): Поперечная сила Q: QIII(z) = RA - F1 - F2 = -0.00023343 - 0.003842 + 0.00943 = 0.0053546; Значения Q на краях отрезка: QIII(0.0565) = 0.0053546 кН; QIII(0.083) = 0.0053546 кН; Изгибающий момент M: MIII(z) = RA z - F1(z - c1) - F2(z - c2) = -0.00023343z - 0.003842(z - 0.023) + 0.00943(z - 0.0565) = 0.0053546z - 0.00044443; Значения M на краях отрезка: MIII(0.0565) = 0.0053546·0.0565 - 0.00044443 = -0.0001419 кНм; MIII(0.083) = 0.0053546·0.083 - 0.00044443 = 0; 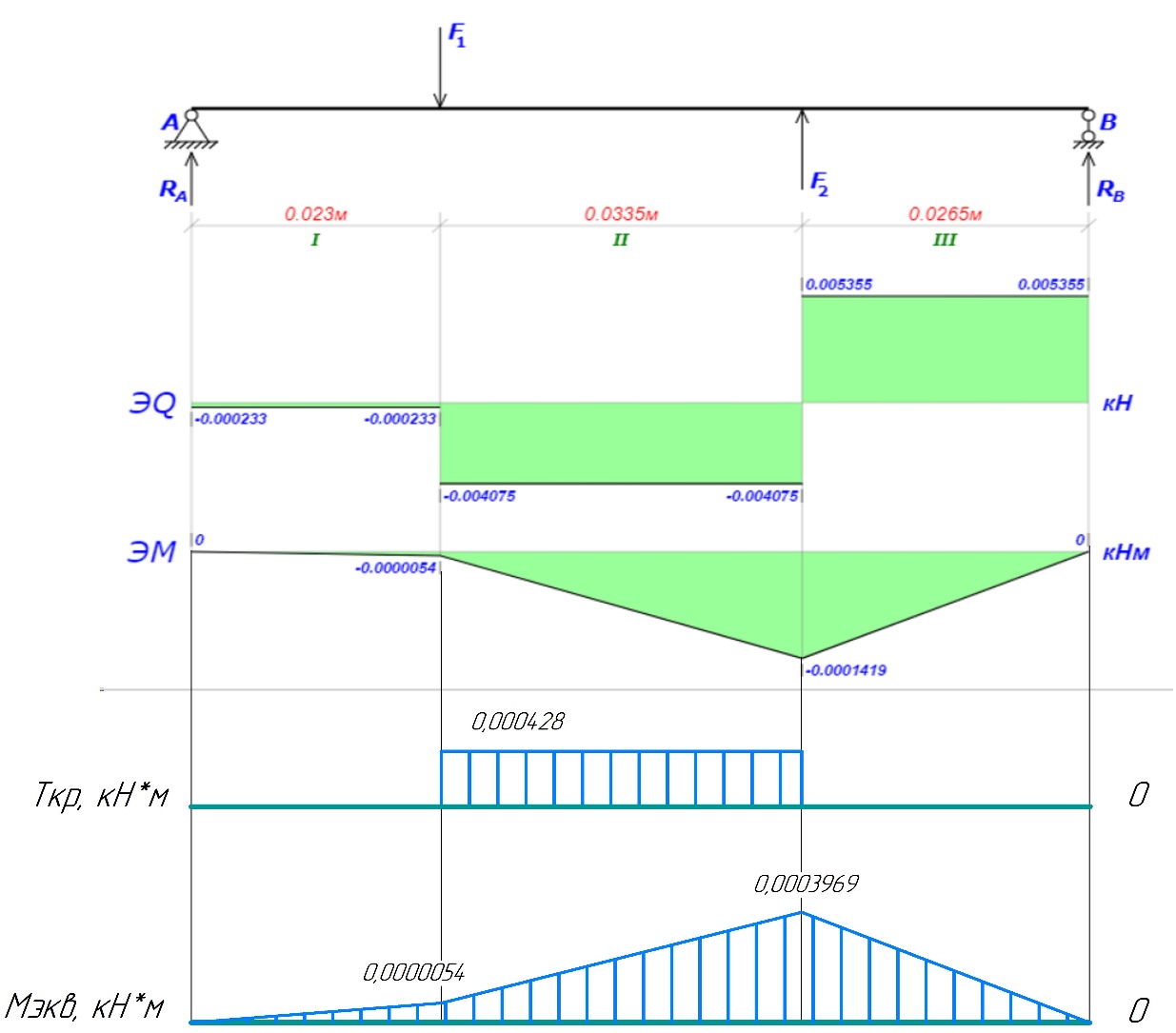 Рисунок 2.6. Эпюра сил и моментов вала 2 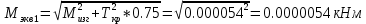 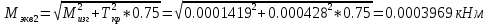 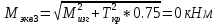 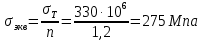 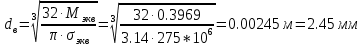 По конструкционным соображениям берём 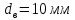 Вал 3   Рисунок 2.7. Схема нагружения вала 3 Реакции опор Сумма моментов всех сил относительно точки B должна равняться нулю: ∑MB = - RA L + ∑qi(bi - ai)(2L - ai - bi)/2 + ∑Fi(L - ci) - ∑Mi = = - RA L + F1(L - c1) + F2(L - c2) = - RA·0.28227 + 0.00885·(0.28227 - 0.0565) + 0.040967·(0.28227 - 0.1825) = = - RA·0.28227 + 0.00885·0.22577 + 0.040967·0.09977 = = - RA·0.28227 + 0.00608534209 = 0 ⇒ ⇒ RA = 0.00608534209/0.28227 = 0.021559 кН; Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = RB L - ∑qi(bi - ai)(ai + bi)/2 - ∑Fici - ∑Mi = = RB L - F1c1 - F2c2 = RB·0.28227 - 0.00885·0.0565 - 0.040967·0.1825 = = RB·0.28227 - 0.0079765025 = 0 ⇒ ⇒ RB = 0.0079765025/0.28227 = 0.028258 кН; Для проверки вычислим сумму проекций всех сил на вертикальную ось: ∑Y = RA + RB - ∑qi(bi - ai) - ∑Fi = = RA + RB - F1 - F2 = = 0.021559 + 0.028258 - 0.00885 - 0.040967 = 0; Построение эпюр Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 0.0565): QI(z) = RA = 0.021559; Значения Q на краях отрезка: QI(0) = 0.021559 кН; QI(0.0565) = 0.021559 кН; Изгибающий момент M: MI(z) = RA z = 0.021559z; Значения M на краях отрезка: MI(0) = 0.021559·0 = 0; MI(0.0565) = 0.021559·0.0565 = 0.0012181 кНм; Участок II (0.0565 ≤ z ≤ 0.1825): Поперечная сила Q: QII(z) = RA - F1 = 0.021559 - 0.00885 = 0.012709; Значения Q на краях отрезка: QII(0.0565) = 0.012709 кН; QII(0.1825) = 0.012709 кН; Изгибающий момент M: MII(z) = RA z - F1(z - c1) = 0.021559z - 0.00885(z - 0.0565) = 0.012709z + 0.00050003; Значения M на краях отрезка: MII(0.0565) = 0.012709·0.0565 + 0.00050003 = 0.0012181 кНм; MII(0.1825) = 0.012709·0.1825 + 0.00050003 = 0.0028193 кНм; Участок III (0.1825 ≤ z ≤ 0.28227): Поперечная сила Q: QIII(z) = RA - F1 - F2 = 0.021559 - 0.00885 - 0.040967 = -0.028258; Значения Q на краях отрезка: QIII(0.1825) = -0.028258 кН; QIII(0.28227) = -0.028258 кН; Изгибающий момент M: MIII(z) = RA z - F1(z - c1) - F2(z - c2) = 0.021559z - 0.00885(z - 0.0565) - 0.040967(z - 0.1825) = -0.028258z + 0.0079765; Значения M на краях отрезка: MIII(0.1825) = -0.028258·0.1825 + 0.0079765 = 0.0028193 кНм; MIII(0.28227) = -0.028258·0.28227 + 0.0079765 = 0; 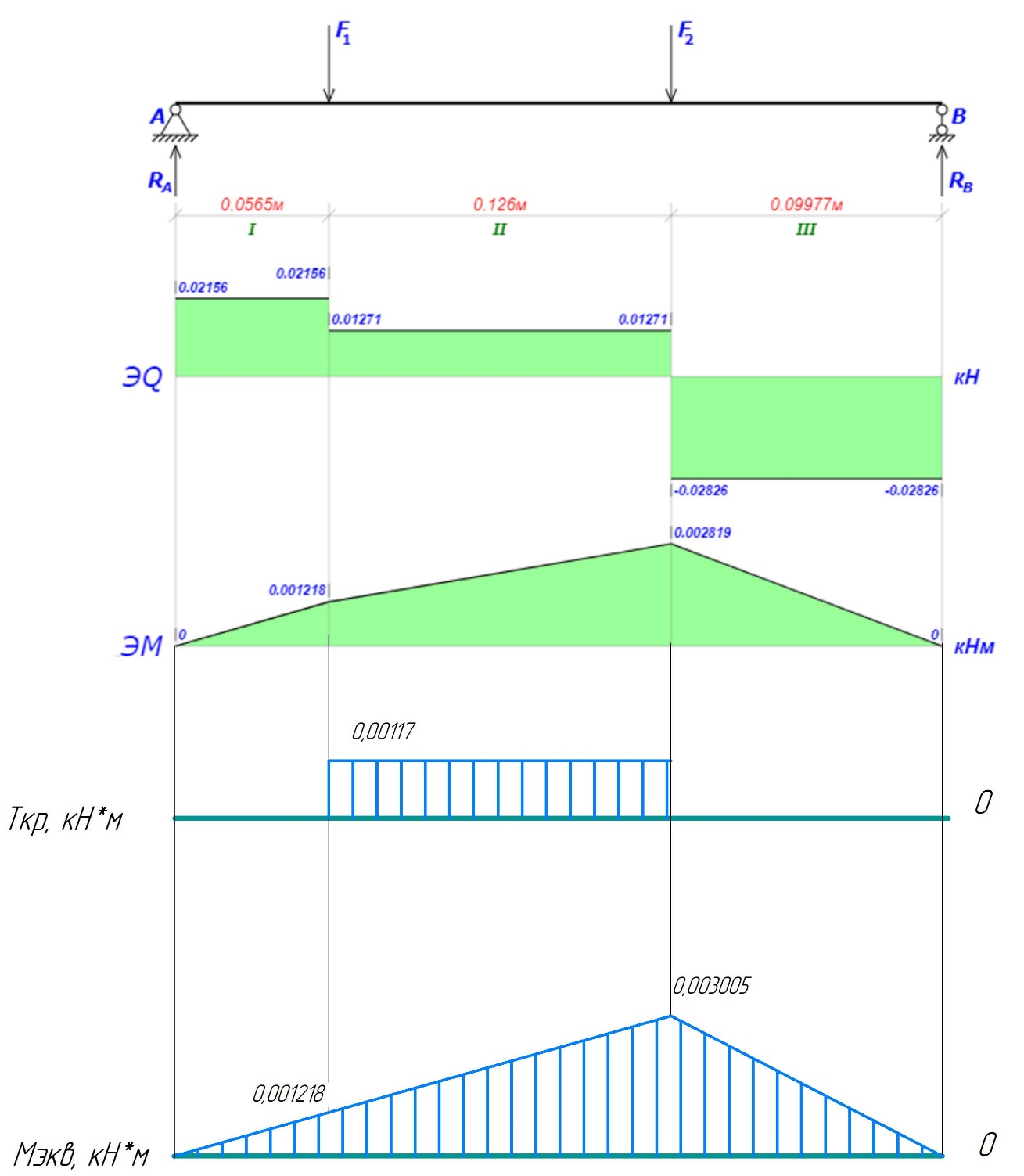 Рисунок 2.8. Эпюра сил и моментов вала 3 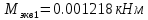 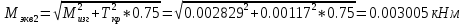 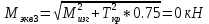 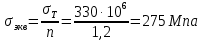 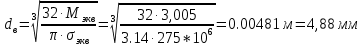 По конструкционным соображениям берём  Вал 4  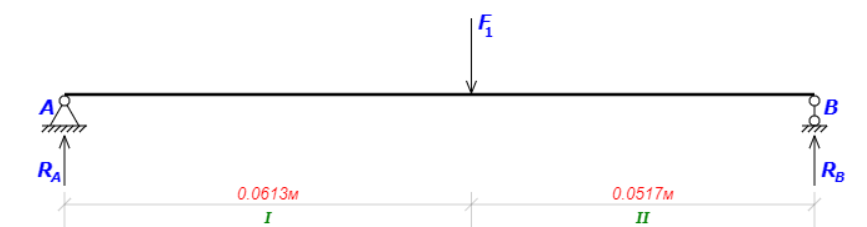 Рисунок 2.9. Схема нагружения вала 4 Реакции опор Сумма моментов всех сил относительно точки B должна равняться нулю: ∑MB = - RA L + ∑qi(bi - ai)(2L - ai - bi)/2 + ∑Fi(L - ci) - ∑Mi = = - RA L + F1(L - c1) = - RA·0.113 + 0.229413·(0.113 - 0.0613) = = - RA·0.113 + 0.229413·0.0517 = = - RA·0.113 + 0.0118606521 = 0 ⇒ ⇒ RA = 0.0118606521/0.113 = 0.10496 кН; Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = RB L - ∑qi(bi - ai)(ai + bi)/2 - ∑Fici - ∑Mi = = RB L - F1c1 = RB·0.113 - 0.229413·0.0613 = = RB·0.113 - 0.0140630169 = 0 ⇒ ⇒ RB = 0.0140630169/0.113 = 0.12445 кН; Для проверки вычислим сумму проекций всех сил на вертикальную ось: ∑Y = RA + RB - ∑qi(bi - ai) - ∑Fi = = RA + RB - F1 = = 0.10496 + 0.12445 - 0.229413 = 0; Построение эпюр Составим аналитические выражения Q(z) и M(z) для каждого участка и вычислим их значения в характерных точках. Участок I (0 ≤ z ≤ 0.0613): Поперечная сила Q: QI(z) = RA = 0.10496; Значения Q на краях отрезка: QI(0) = 0.10496 кН; QI(0.0613) = 0.10496 кН; Изгибающий момент M: MI(z) = RA z = 0.10496z; Значения M на краях отрезка: MI(0) = 0.10496·0 = 0; MI(0.0613) = 0.10496·0.0613 = 0.0064341 кНм; Участок II (0.0613 ≤ z ≤ 0.113): Поперечная сила Q: QII(z) = RA - F1 = 0.10496 - 0.229413 = -0.12445; Значения Q на краях отрезка: QII(0.0613) = -0.12445 кН; QII(0.113) = -0.12445 кН; Изгибающий момент M: MII(z) = RA z - F1(z - c1) = 0.10496z - 0.229413(z - 0.0613) = -0.12445z + 0.014063; Значения M на краях отрезка: MII(0.0613) = -0.12445·0.0613 + 0.014063 = 0.0064341 кНм; MII(0.113) = -0.12445·0.113 + 0.014063 = 0; 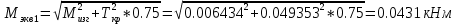 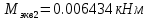 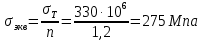 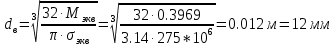 По конструкционным соображениям берём 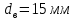 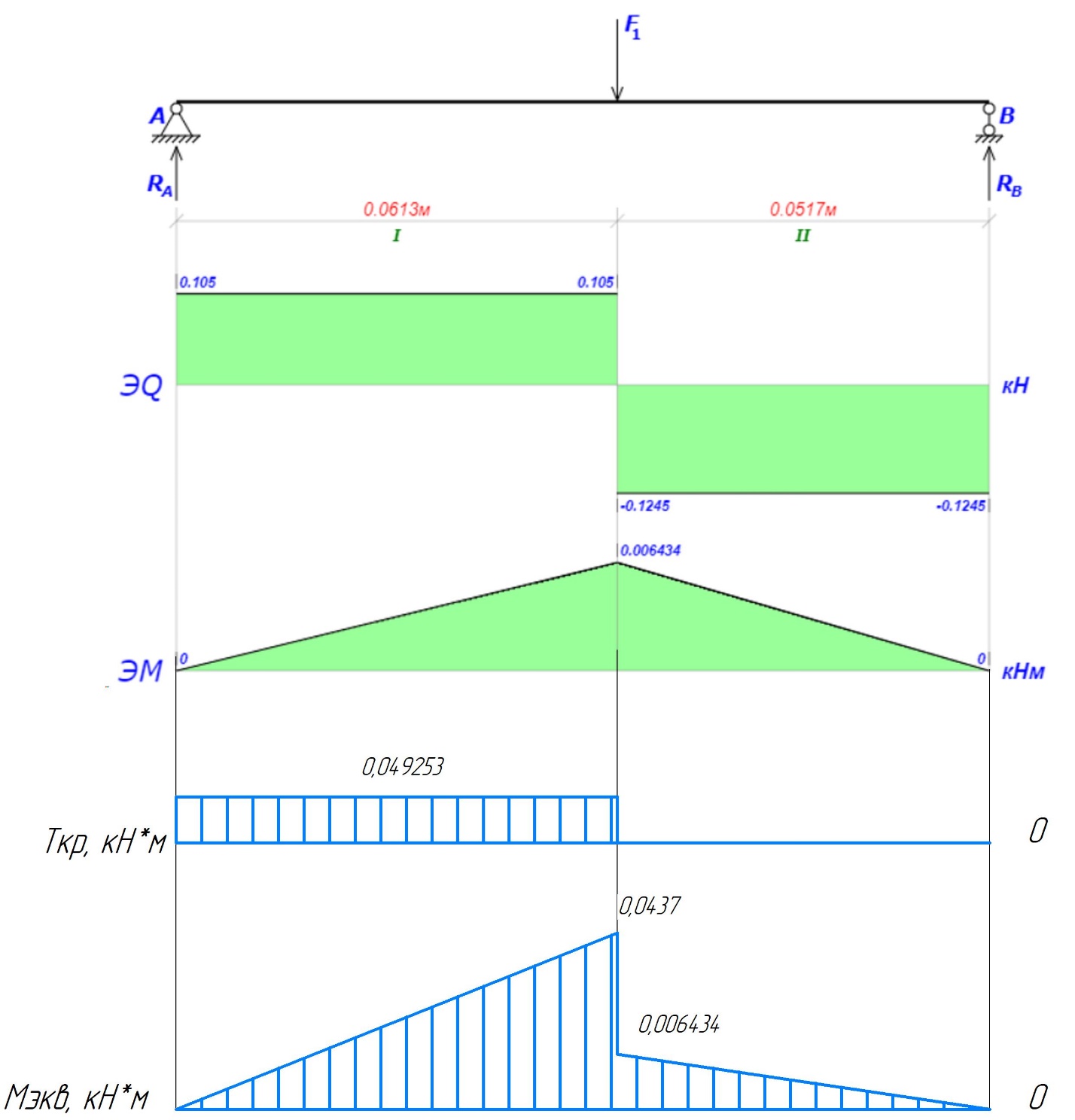 Рисунок 2.10. Эпюра сил и моментов вала 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

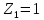
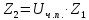
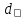
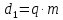
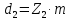
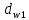
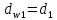
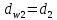
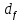
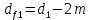
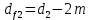
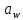
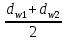
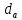
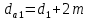
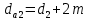
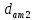
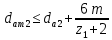
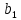
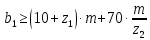 +25
+25