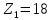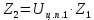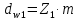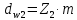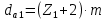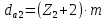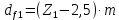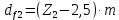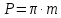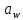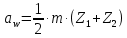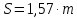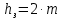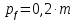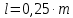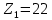Курсовая работа по деталям машин. ПЗ без подписи. Курсовой проект по дисциплине Детали машин и основы конструирования
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
ЧАСТЬ 2. РАСЧЕТ РЕДУКТОРАДля дальнейших расчётов требуется определить общее передаточное число, которое находится по следующей формуле: 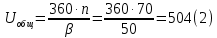 где n – количество оборотов ручки, для поворота установки на β градусов. Исходя из общего передаточного отношения подбираются передаточные числа для цилиндрических и червячной передач так, чтобы их произведение было равно общему передаточному числу. 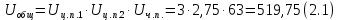 2.1 Цилиндрическая передача2.1.1. Определение геометрических параметров цилиндрическойЗацепление зубчатых колес эквивалентно качению без скольжения окружностей с диаметрами dw1 и dw2 (рис. 2), которые называются начальными окружностями. 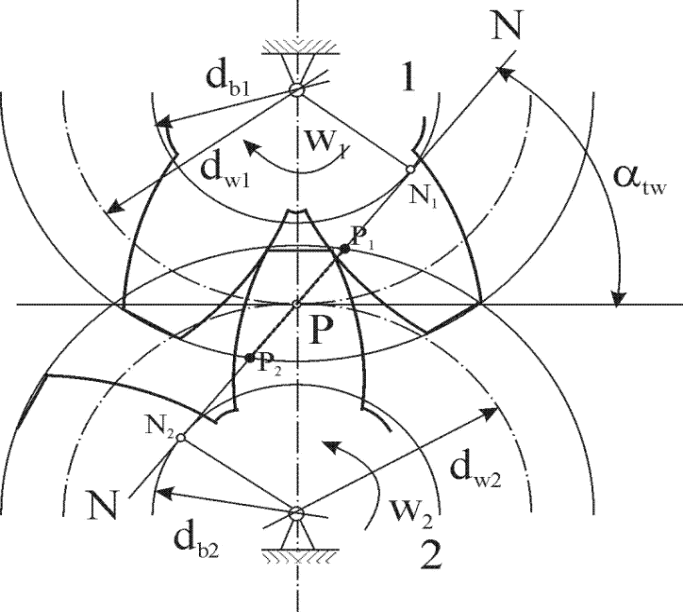 Рисунок 2. Образование эвольвентных профилей Для дальнейших расчётов требуется определить модуль передачи (характеристика масштаба колеса). Исходя из ГОСТ 9563–80 был выбран модуль m=1,5 мм. Подобрав модуль, следует вычислить остальные геометрические параметры передачи: Таблица 1. Цилиндрическая передача 1
Таблица 2. Цилиндрическая передача 2
где Z – число зубьев; 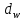 – делительный диаметр; – делительный диаметр;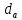 – диаметр вершин зубьев; – диаметр вершин зубьев;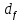 – диаметр впадин; – диаметр впадин;P– шаг зубьев; S – толщина зуба; 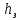 – глубина захода; – глубина захода;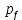 – радиус кривизны у основания; – радиус кривизны у основания;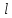 – радиальный зазор. – радиальный зазор.Ширину зубчатых колес выбирают в соответствии с установленными эмпирическими соотношениями Ψa=b/aw: для ЦП 1 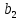 =Ψa =Ψa aw1 =0,2 aw1 =0,2 54 = 10,8 = 11 мм; 54 = 10,8 = 11 мм;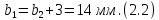 для ЦП 2 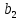 =Ψa =Ψa aw2 =0,2 aw2 =0,2 62,25 = 12,45 = 13 мм; 62,25 = 12,45 = 13 мм;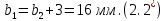 Крутящий момент на шестерне (T1) ЦП 1 принимаем равным крутящему моменту на ручке редуктора 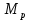 , т.е. , т.е.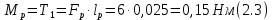 На колесе крутящий момент (T2) ЦП 1 вычисляется по формуле: 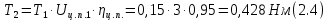 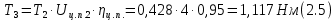 где 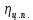 – КПД цилиндрической передачи ( – КПД цилиндрической передачи (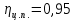 ). ). Момент на червяке определяется по формуле: 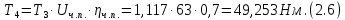 Где 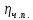 – КПД червячной передачи=0,7 – КПД червячной передачи=0,72.1.2. Расчёт прямозубой цилиндрической передачиДля изготовления шестерни и колеса используется ст40х со следующими характеристиками: Твёрдость шестерни: HB1=250 HB; Твёрдость колеса: HB2=240 HB; Предел прочности ст40х: σB=850 МПа; Предел текучести ст40х: σT=550 МПа; Модуль упругости: 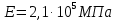 .; .;Угол зацепления: αt = 20º; Коэффициент динамической нагрузки: 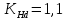 ; ;Коэффициент расчётной нагрузки: 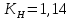 . .Пределы контактной выносливости для шестерни и колеса вычисляются по формуле: 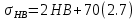 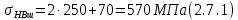 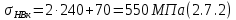 Далее проводится расчёт сил, действующих в цилиндрических передачах. Будем рассматривать момент зацепления в полюсе, силы трения ввиду малости не учитываются. Окружная составляющая силы (вдоль оси х), передающая вращение с одного колеса на другое, для всех зубчатых колес: Для 1 Ц.П.: 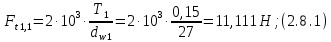 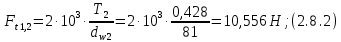 Для 2 Ц.П.: 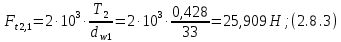 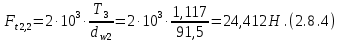 где 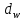 –делительный диаметр в мм. –делительный диаметр в мм.Радиальная Fr и осевая Fz силы доля прямозубых колёс определяются по формулам: Для 1 Ц.П.: 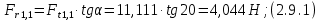  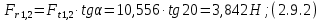 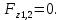 Нормальная к поверхности зуба сила: 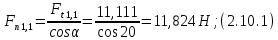 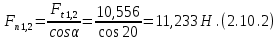 Для 2 Ц.П.: 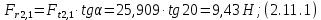 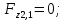 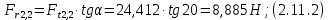 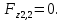 Нормальная к поверхности зуба сила: 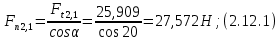 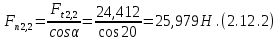 2.1.3. Расчёт зубьев цилиндрических передач на изгиб.Данный расчёт – основной для зубьев открытых передач. Этот расчет является основным для зубьев открытых передач. Для оценки прочностной надежности зубчатой передачи необходимо иметь уравнение, связывающие максимальные напряжения в опасном сечении с внешней нагрузкой на зуб и размерами опасного сечения (параметрами передачи). Точный расчет зубьев возможен лишь методами теории упругости. В инженерном расчете зуб рассматривают как консольную балку (стержень) постоянного сечения с нагрузкой, распределенной по линии контакта, и требуемую зависимости напряжений от сил и размеров сечения принимают по формулам сопротивления материалов. Далее значения номинальных напряжений уточняют введением теоретического коэффициента концентрации напряжений. Условие прочностной надежности зуба по допускаемым напряжениям изгиба имеет обычный вид: σ F ≤ [σ F] (2.13) где σF – максимальное напряжение изгиба в опасном сечении зуба; [σF] – допускаемое напряжение изгиба для материала зуба. Местные напряжения от изгиба вычисляются по следующей формуле: 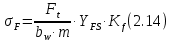 где 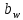 – ширина зубчатого колеса; – ширина зубчатого колеса;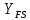 – коэффициент формы зубьев ( – коэффициент формы зубьев (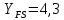 ); );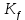 – коэффициент нагрузки ( – коэффициент нагрузки (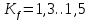 ); );m –модуль, а допускаемые напряжения изгиба: 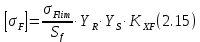 где 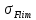 – предел выносливости зубьев ( – предел выносливости зубьев (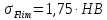 ); );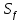 –коэффициент запаса прочности ( –коэффициент запаса прочности (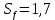 ); );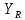 – коэффициент, учитывающий шероховатость переходной поверхности (при полировании – коэффициент, учитывающий шероховатость переходной поверхности (при полировании 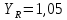 ); );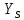 – коэффициент, учитывающий чувствительность материала к концентрации напряжений и градиент напряжений, определяемый в зависимости от модуля ( – коэффициент, учитывающий чувствительность материала к концентрации напряжений и градиент напряжений, определяемый в зависимости от модуля (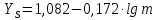 ); );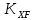 – коэффициент, учитывающий влияние размеров – коэффициент, учитывающий влияние размеров ( 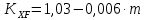 ). ).Для ЦП 1: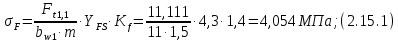 Для ЦП 2: 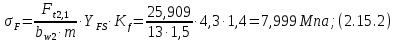 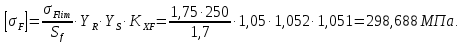 Условие прочностной надежности зуба по допускаемым напряжениям изгиба соблюдается. 2.1.4. Расчёт зубьев цилиндрической передачи на контактную прочность.Данный расчёт сводится к удовлетворению следующего условия: контактные напряжения в зубьях σH должны быть равны или меньше допускаемых [σH]. Расчет ведут для зацепления в полюсе, так как выкрашивание начинается у полюсной линии (на ножке), причем полюсная линия прямозубых передач находится в зоне однопарного зацепления. Контактные напряжения вычисляются по формуле: 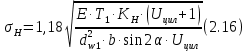 Допускаемые контактные напряжения находятся следующим образом: 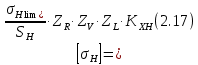 где 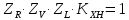 – коэффициенты, учитывающие влияние шероховатости, окружной скорости, смазки, размеров; – коэффициенты, учитывающие влияние шероховатости, окружной скорости, смазки, размеров;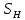 – коэффициент запаса прочности (при однородной структуре зуба: – коэффициент запаса прочности (при однородной структуре зуба: 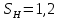 , при поверхностных упрочнениях: , при поверхностных упрочнениях: 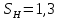 ); );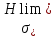 – предел контактной выносливости ( – предел контактной выносливости (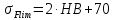 ). ).Для ЦП 1: 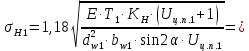 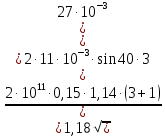 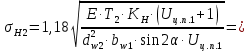 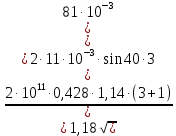  Для ЦП 2: 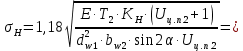 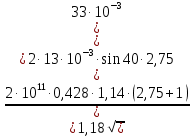 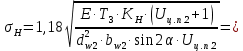 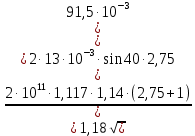 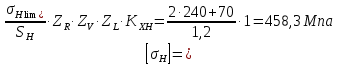 Условие прочностной надежности зуба на контактную прочность соблюдается. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||