Курсовой проект по дисциплине Железобетонные и каменные конструкции
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
7.3 Расчет продольного ребра плиты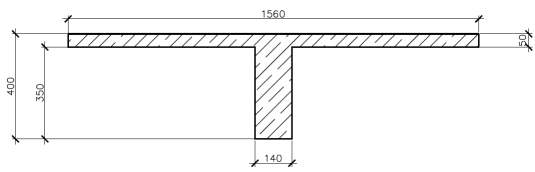 Рисунок 11 – Поперечное сечение продольного ребра Таблица 9 – Нагрузки на 1 м ребристой плиты
С учетом коэффициента надежности по классу ответственности здания: Для расчетов по I группе предельных состояний: 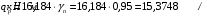 ; ;Для расчета по II группе предельных состояний: полная: 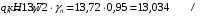 ; ;длительная: 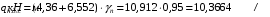 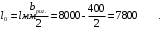 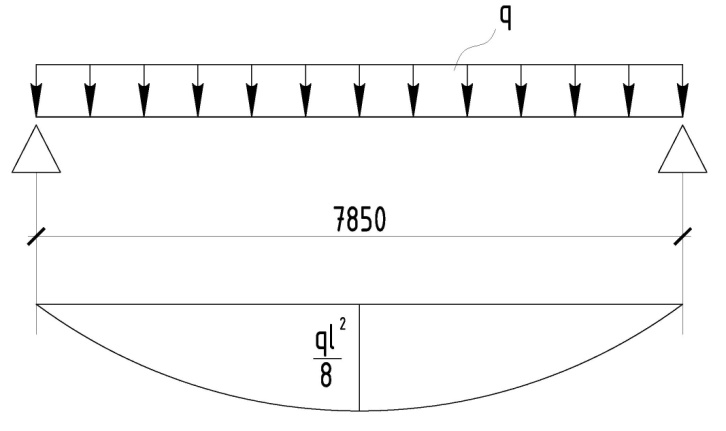 Рисунок 12 – Расчетная схема продольного ребра h0=400-30=370мм. Класс предварительно напрягаемой арматуры А 600 Rs=520 МПа Rs ser=590 МПа Расчетные усилия: Для расчетов по I группе предельных состояний: 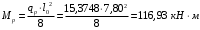 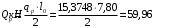 Для расчетов по II группе предельных состояний: 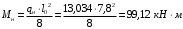 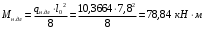 Величина предварительного напряжения в соответствии с /9/ ( п.2.2.3.1) назначается равным σsp = 0,9∙ Rs,n = 0,9∙600 = 540 МПа. Определяем положение нейтральной оси 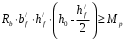 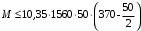 116,93·106 Н·мм < 278,52·106 Н·мм Так как условие выполняется, то граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной 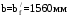 Определяем коэффициент статического момента αm 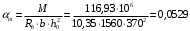 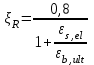 где 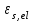 для напрягаемой арматуры определяется по формуле: для напрягаемой арматуры определяется по формуле: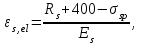 где: σsp - предварительное напряжение в арматуре с учетом всех потерь и γsp = 0,9. Так как согласно /9/ в общем случае суммарные потери должны быть не менее 100 МПа и 30% от величины предварительного напряжения, то σsp определяется по формуле 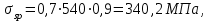 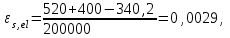 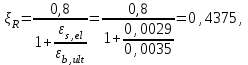 Проверяем условие: ξ = 0,054< ξR = 0,4375; η = 0,973. Условие выполняется. Определяем коэффициент, учитывающий предварительное напряжение арматуры 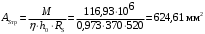 Принимаем 4 стержня Ø16 А 600, Аs= 804 мм2. Расчёт прочности сечений, наклонных к продольной оси. Из условия свариваемости принимаем поперечные стержни диаметром 8 мм класса А400 с числом каркасов – 2 с шагом поперечных стержней s=150 мм. Аsw = 2х50,3=100,6 мм2 Rsw = 285 МПа, Rbt = 0,9∙0,9=0,81 МПа Еs = 200000МПа Еb = 27000МПа Проверяем условие: 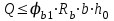 , ,где φb1 =0,3 (/9/ п.6.2.34); тогда: 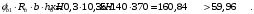 Условие выполняется, прочность по наклонной полосе между трещинами обеспечена. Проверяем условие: 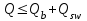 ; ;где Qb - поперечное усилие, воспринимаемое бетоном: 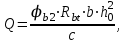 где: φb2 = 1,5; с - длина проекции наиболее опасного наклонного сечения на продольную ось элемента, равная 3h0. 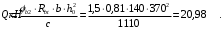 Qsw - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Поперечную силу Qsw определяют по формуле: 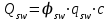 где: φsw=0,75 (/9/ п.6.2.34); с - длина проекции наиболее опасной наклонной трещины на продольную ось элемента равная 2h0; qsw - усилие в поперечной арматуре на единицу длины элемента, определяемое по формуле: 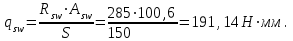 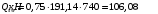 Проверяем условие: 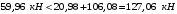 ; ;Условие выполняется, следовательно, прочность наклонного сечения обеспечена. |